单自由度有限循环行走机构运动控制及参数识别

危清清，林云成，肖 轩，陈 磊，刘 宾，王耀兵

(1.空间智能机器人系统技术与应用北京重点实验室，北京100094；2.中国空间技术研究院北京空间飞行器总体设计部，北京100094；3.清华大学航天学院，北京100084)

1 引言

双足机器人是目前机器人的研究热点之一，其行走控制分为基于参考轨迹的控制和基于模型的动态控制。基于参考轨迹的方法是双足机器人中较为常见的算法，通过控制关节力矩使关节按照事先规划好的参考轨迹运动，可实现复杂动作。但算法实现较复杂，效率低，不能深入揭示双足行走稳定性、适应性和高效率的内在机理[1]。基于模型的动态控制方法借鉴已有的物理模型对行走过程进行简化，如倒立摆模型、被动步态模型，弹簧质量模型等。其中被动步态模型大大简化了双足行走机构，通过研究双足运动的内在固有特点，能揭示双足行走高效、稳定的内在机理。

有限循环行走(Limit Cycle Walking)是被动步态模型的延伸，可使行走系统在步态周期的每个瞬间都能获得稳定的周期性行走，而不需要局部维持行走运动的稳定。利用物理动力学和被动性，有限循环行走机构(Limit Cycle Walkers)在产生自然和节能的动态步态方面具有明显优势[2-3]。由于时间和空间的不可逆性，准确地产生目标行走速度对于有限循环行走系统来说具有挑战性。因此，在每一步中对离散时间段和空间段的整体规划对于行走系统目标速度控制是必要的。

Hobbelen等[4-5]研究了如何改变行走速度，何种方式在节能上是有益的，以及行走速度如何影响行走系统在有限循环行走中处理干扰的能力。Kajita等[6]提出了通过改变双足行走系统的立足点来修改支撑相的初始条件，利用基于PD反馈控制器控制行走速度。此外，Juang等[7]提出一种学习方案，训练神经模糊控制器使其尽可能地遵循设计的轨迹，以一定的速度产生行走步态。针对限制环行走的收敛步态，Xiao等[8-9]提出一种基于模型的控制，以便在处理干扰时保持目标步行速度。

然而，作为基于模型的控制器的属性，其性能通常取决于所有物理模型参数。因此，用于预测质量、尺寸等动力学参数的参数识别方法[10-11]成为解决方案，并且提出能够处理预测误差的鲁棒控制器作为解决该问题的另一种选择。由于预测参数误差直接反映了行走系统的性能，而基于模型的控制器的性能可以有助于预测物理参数，优化行走性能。

本文提出一种基于模型的反馈控制器，以实现有限循环行走，且根据行走过程中神经网络预测物理参数，以减少行走机构产生的目标状态物理参数对基于模型的控制器的依赖性。

2 主动组合无框轮

组合无框轮(Combined Rimless Wheel，CRW)的模型搭建、动力学分析、碰撞过程建模是本文控制器的设计基础。

2.1 建模

平面主动CRW的模型如图1所示，它由2个八腿无框轮(Rimless Wheels，RWs)组成一个车身框架。每个RW的质量为m，两腿间夹角为α=腿长l，支撑腿与重垂线的夹角为θ，g是重力加速度。框架上的电动机在后站立腿和车身框架之间施加关节转矩u，可以驱动CRW在平地上行走，作如下假设：

1)前后站立腿始终与地面接触而不会滑动；

2)关于所有框架的质心的惯性矩可以忽略不计；

3)前后RW完全同步或旋转保持关系θ1=θ2。

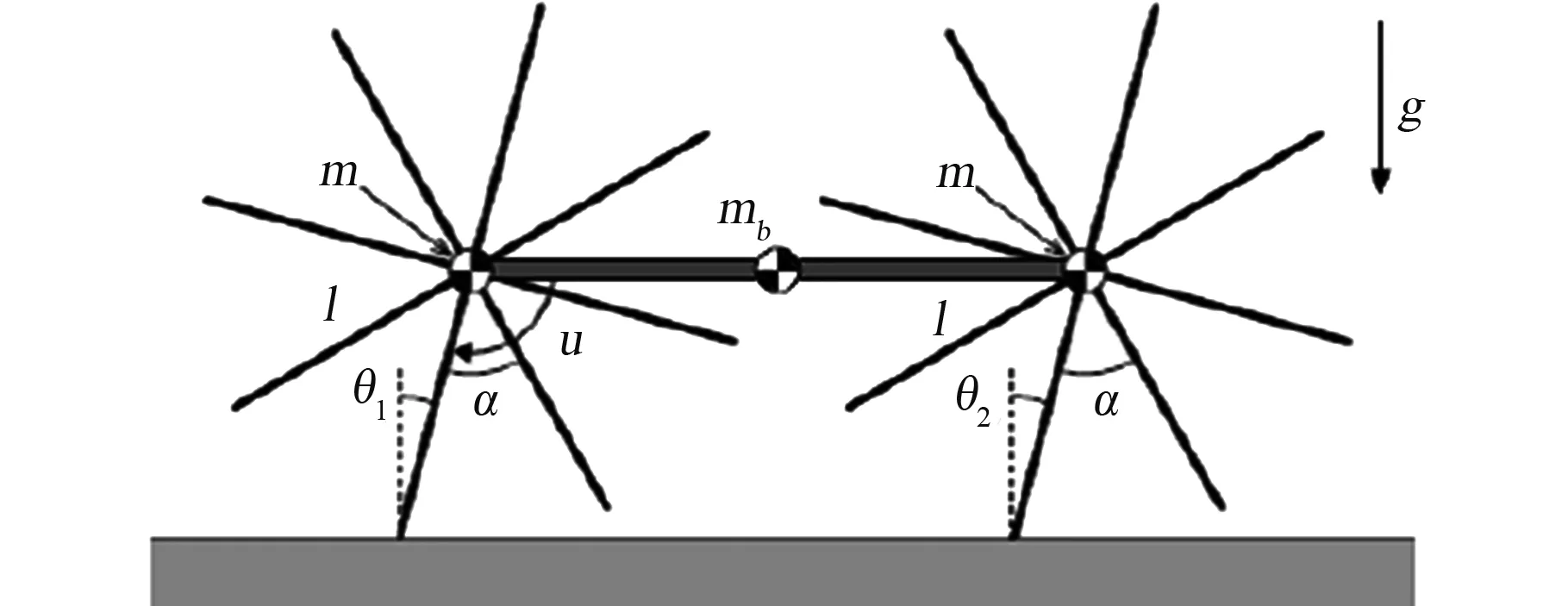
图1 平面主动组合无框轮Fig.1 A planar active CRW

在CRW中，通过步进时段和步长之间的比率来计算稳定步行速度。因此，可通过恒定步长控制步长周期来产生目标稳步行走速度状态。

2.2 运动方程及其线性化

1个四连杆机构由车身框架、2个站立腿和地面组成，施加关节转矩相当于施加踝关节转矩。此外还考虑接头粘度的转矩fv=-kvθ，其中kv是粘滞摩擦系数。因此，后部RW的动力学与具有踝关节转矩和粘性摩擦的主动RW的动力学方程相同，即式(1)：

其中m是单个RW的质量，mb是连接工装的质量，则M=mb+2 m是CRW的总质量，单位kg。θ=θ1=θ2是站立角度，ω = g/l。 通过在0附近时的线性化θ≈sinθ[12]，RW动态的状态空间实现可表示，见式(2)。

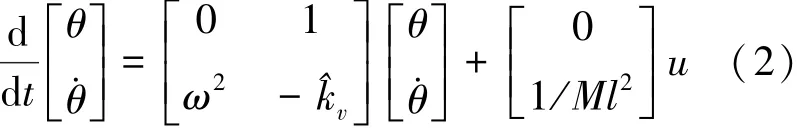
其中^kv=kv/Ml2。 因此将式(2)表示为式(3)：

需要注意的是，式(2)仅用于控制系统设计。所有模拟都通过式(1)中的动力学方程进行。可以看出，当基于式(1)设计控制系统时，由于式(2)中的线性化，模拟中生成的行走状态不能完全满足预期结果。根据本文的仿真结果，误差是可以接受且可以消除的。

2.3 碰撞方程

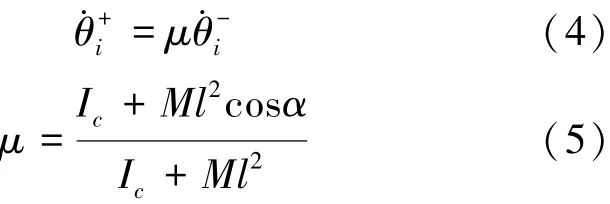
其中，Ic代表CRW的惯性矩。本文忽略惯性矩的影响 Ic=0( )，则μ简化为μ=cosα。

3 控制律

3.1 控制器设计

在控制系统中，转矩是基于当前时间和状态动态更新的。冲击时刻定义为0 s，并且每次冲击后立即重置时间参数。转矩必须提供足够的动能以使CRW克服潜在的障碍。另外，如果步行速度太快以至于在下一次撞击之前无法完成控制，则无法保证目标步行速度。

本文的控制规则是基于恒定转动力矩控制器提出的，电机遵循恒定转矩策略而不是设计指定的位置轨迹。即当干扰发生时，行走系统可以根据当前状态和目标状态提出新的路线规划。通过更新休息时间的控制计划，可以处理干扰并且可以保证目标行走状态。

基于式(2)，可以得到RW的动力学方程。因此，微分方程·x=Ax+B u的解，在第i+1次撞击之前的状态向量可由在第i次撞击之后的状态量表示[11]，见式(7)：

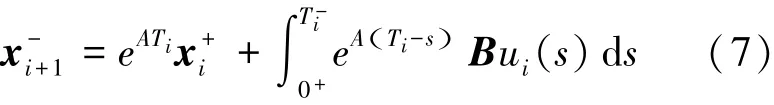
类似地，在t时，状态向量xit()可以由时间t和初始状态向量xi0()表示为式(8)：

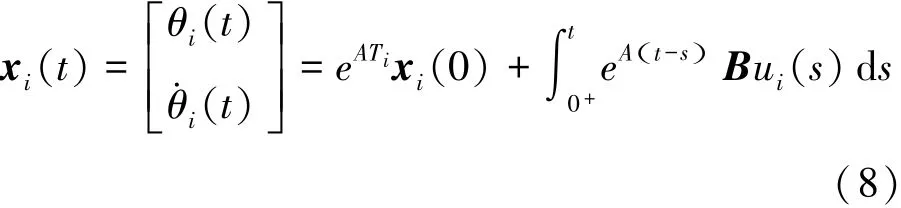
因此，在t时，本文假设为剩下的时间T*s-t保持恒定的控制输入uit()，以产生如下的终端条件 xiTi( )[12]，见式(9)。

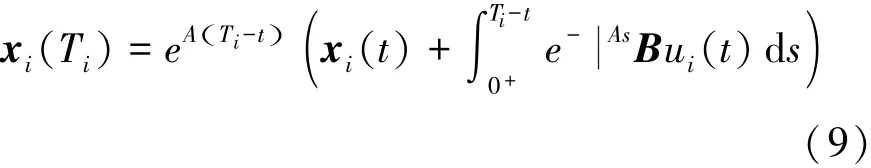
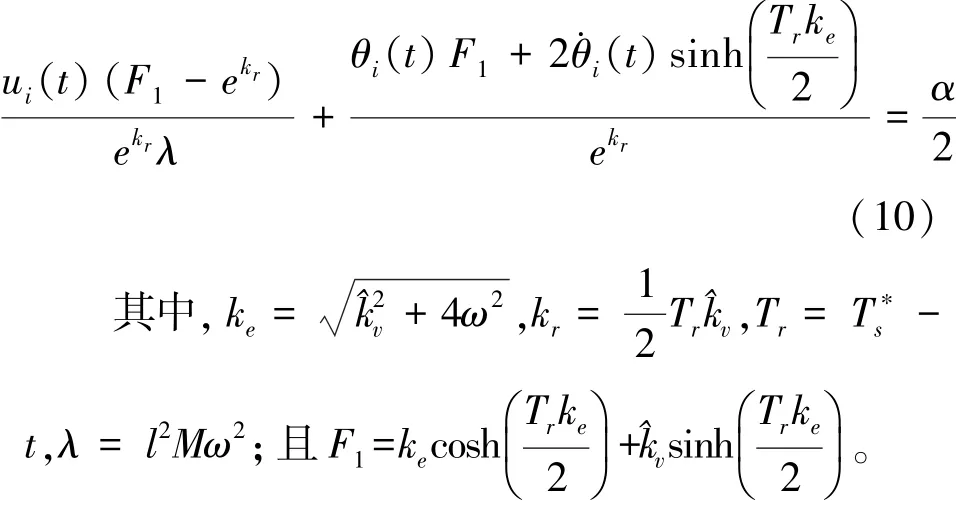
因此，在分析上述角位置方程后，导出uit()以产生目标步长周期状态Ti=T*s见式(11)：

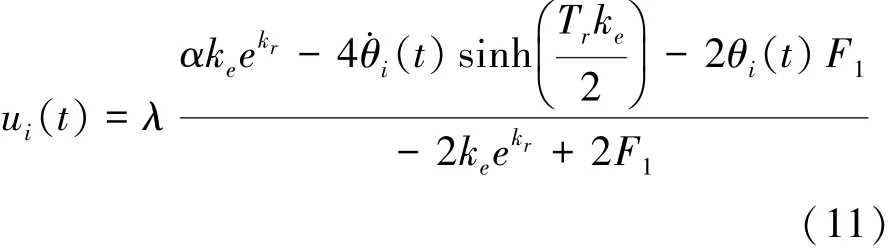
尽管已经提出了控制律，然而存在式(12)：

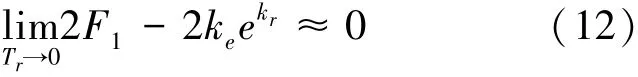
系统误差会经由式(11)产生。在这里，提出一个简单的解决方案：当Tr＜0.001时，令uit()=0。

另外，粘度摩擦的物理参数kv通常不能准确得到，这明显影响了控制器的性能。其他参数M和l也被认为是未知参数。因此，在式(11)计算输入转矩时，在一定的合理范围内M、l和kv全部由Mp、lp和kvp的预测参数代替。反馈控制的流程图如图2所示。如果CRW可以不断地反馈行走实时的状态，且控制系统不断地基于当前时间t和步行状态xit()通过式(11)计算新的控制输入uit()，则可以产生目标步行速度并且提高处理干扰的能力。此外，基于模型的控制动态地更新控制转矩，是难以预先分析每个步骤中的轨迹的。反馈控制的稳定性将是本文未来需要研究的工作。

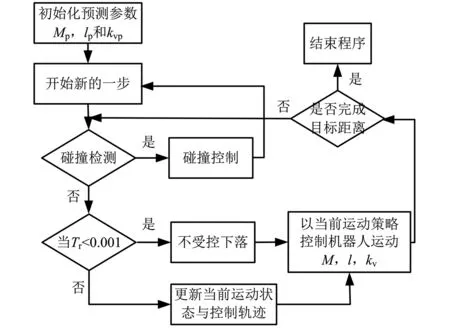
图2 控制流程图Fig.2 Flow chart of control

3.2 仿真结果

为测试控制器的性能，在预测参数下进行数值模拟。使RW以每步0.4 s的目标速度行走，选择了2组特定的预测参数：一组与实际物理参数完全相等，另一组与实际值存在一定的误差(表2)。详细的实际物理参数和两组预测参数列于表1和表2中。

表1 物理参数Table 1 Physical parameters

表2 模拟的预测参数Table 2 Prediction parameters of simulation

本文进行了仿真模拟并记录步态特性，在两组预测参数下保证目标步行速度，并在所有步骤期间产生步长周期步态0.399996 s，与目标周期0.4 s误差很小(0.001%)。另外，本文针对两组不同工况的扭矩变化曲线和庞加莱映射图进行了分析。图3和4分别显示不同集合控制转矩的变化。当预测参数恰好等于物理参数时，每个步骤中的控制转矩具有由式(8)中的线性化引起的一些小幅波动(图3)。相反的，控制转矩明显改变以处理由不精确模型引起的干扰，并且当剩余时间接近0时，转矩会急剧增加或减少(图4)。本文还针对庞加莱映射进行分析，以反映步行机器人的收敛速度，两种情况给出另一个有趣的特性：具有较大预测误差的模拟具有更快的收敛速度(图6)，而图5的收敛速度却较慢，这可以通过减速效应来解释[13]。

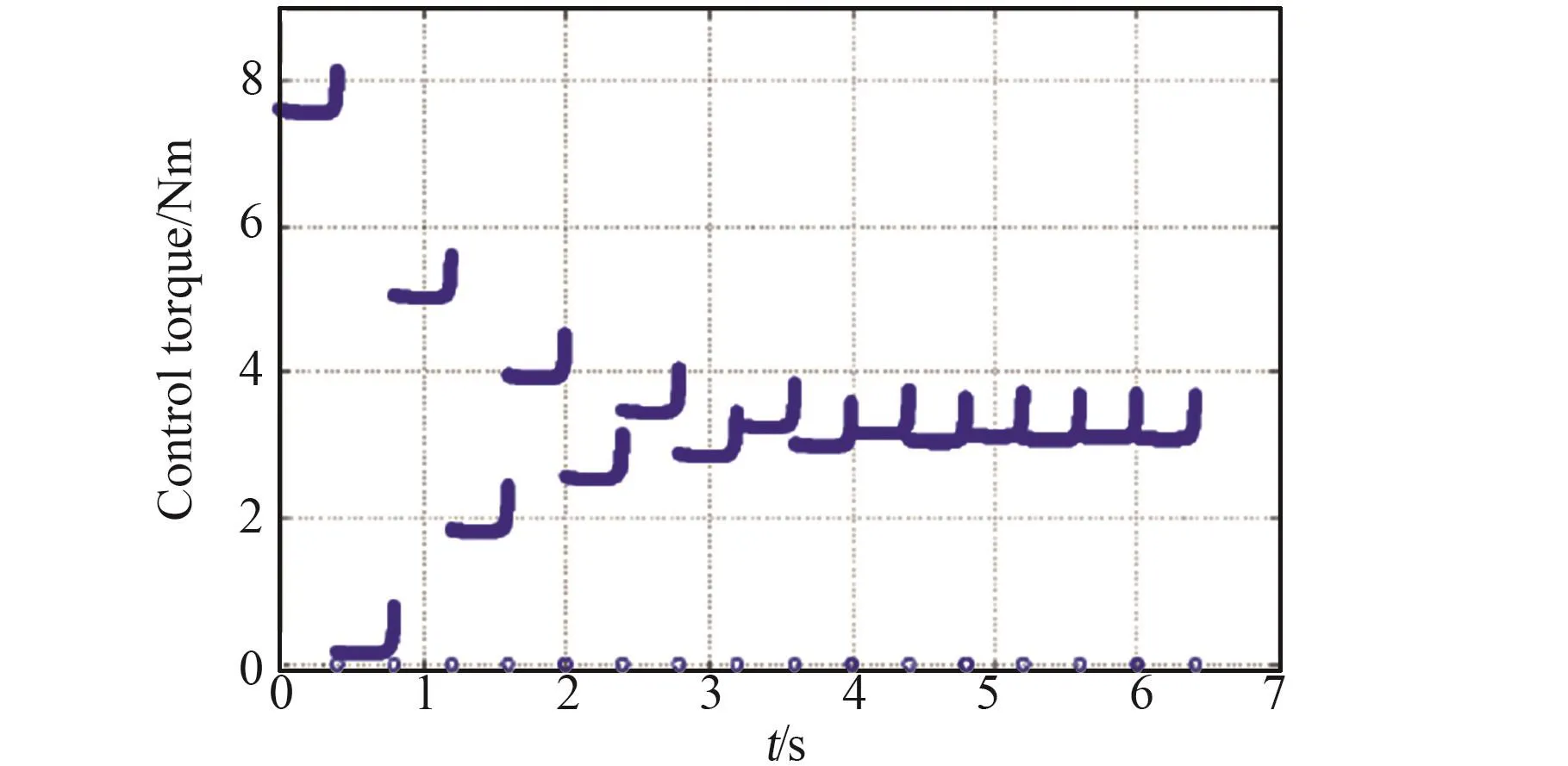
图3 在集合1的预测参数下控制输入的时间演变Fig.3 Time-evolution of control input under the prediction parameters of Set 1

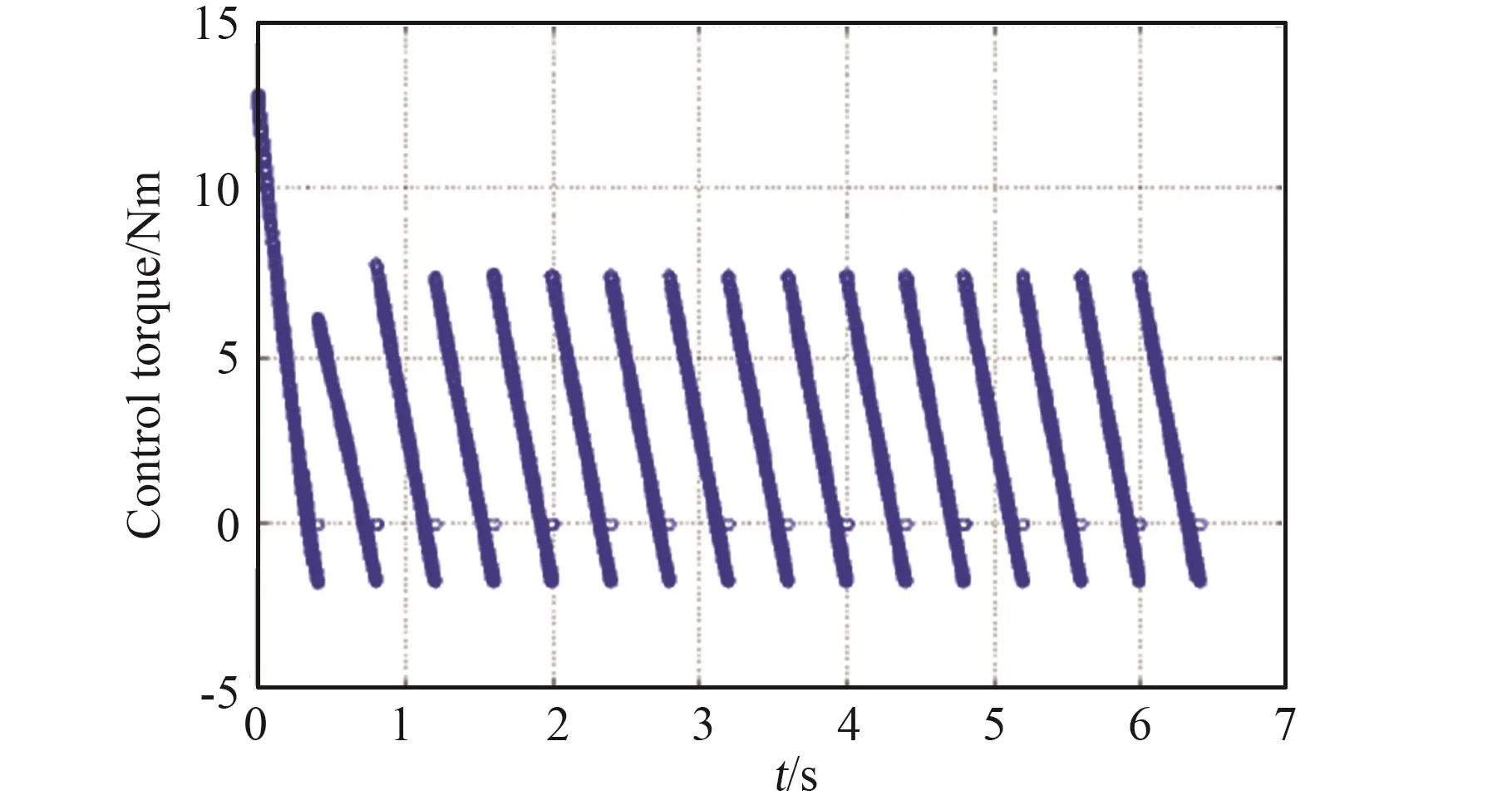
图4 在集合2的预测参数下控制输入的时间演变Fig.4 Time-evolution of control input under the prediction parameters of Set 2

在不同的预测参数组下进行40次模拟以测试边界条件。在每次模拟中，行走系统由反馈控制驱动，通过使用1组随机预测参数以目标步行速度，每步0.4 s，走40步。实际参数与表1相同，并且预测参数在表3的足够范围内随机选择。当行走时间误差大于0.1%(总共0.016 s)时，模拟将被标记为失败。通过分析故障情况下的预测参数，可以发现大致的预测参数范围。

图5 在集合1的预测参数下的庞加莱映射Fig.5 Poincare Map under prediction parameters of Set 1

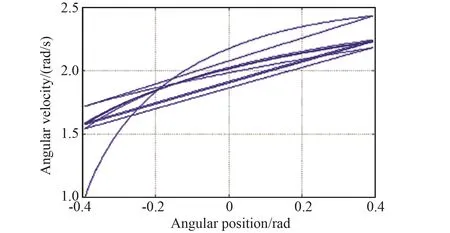
图6 在集合2的预测参数下的庞加莱映射Fig.6 Poincare Map under prediction parameters of Set 2

表3 模式信息Table 3 The pattern information

模拟的分布如图7所示，带有粉红色星形的点意味着真实的物理参数，并且发现了3个失败案例作为红点案例。结果表明，m和l的预测参数都比真实的预测参数低，可能导致故障情况。然而，如果有一步的初始角速度非常快，则控制器将错误地设计行走轨迹，并且在撞击负值之前立即制定计划角速度，且在控制完成之前就会发生撞击是失败的情况。因此，从定性上讲，当物理参数不清楚时，在合理范围内的正预测误差将是一个不错的选择。

本文将反馈控制的3个属性总结如下：

1)当各种预测参数接近真实物理参数时，反馈控制具有一定的适应性以保持目标速度。这种控制对正预测误差具有较强的适应性，而对负预测误差的适应性稍弱，存在失败的可能；

2)转矩的波动是由线性化和预测误差引起的。预测误差偏离越大，每步的转矩变化速度越快。另一方面，即使预测参数与物理参数完全相等，线性化的误差也会引起力矩微小的波动；

3)预测参数可能会对一些步态属性造成影响，例如收敛速度和能量效率。

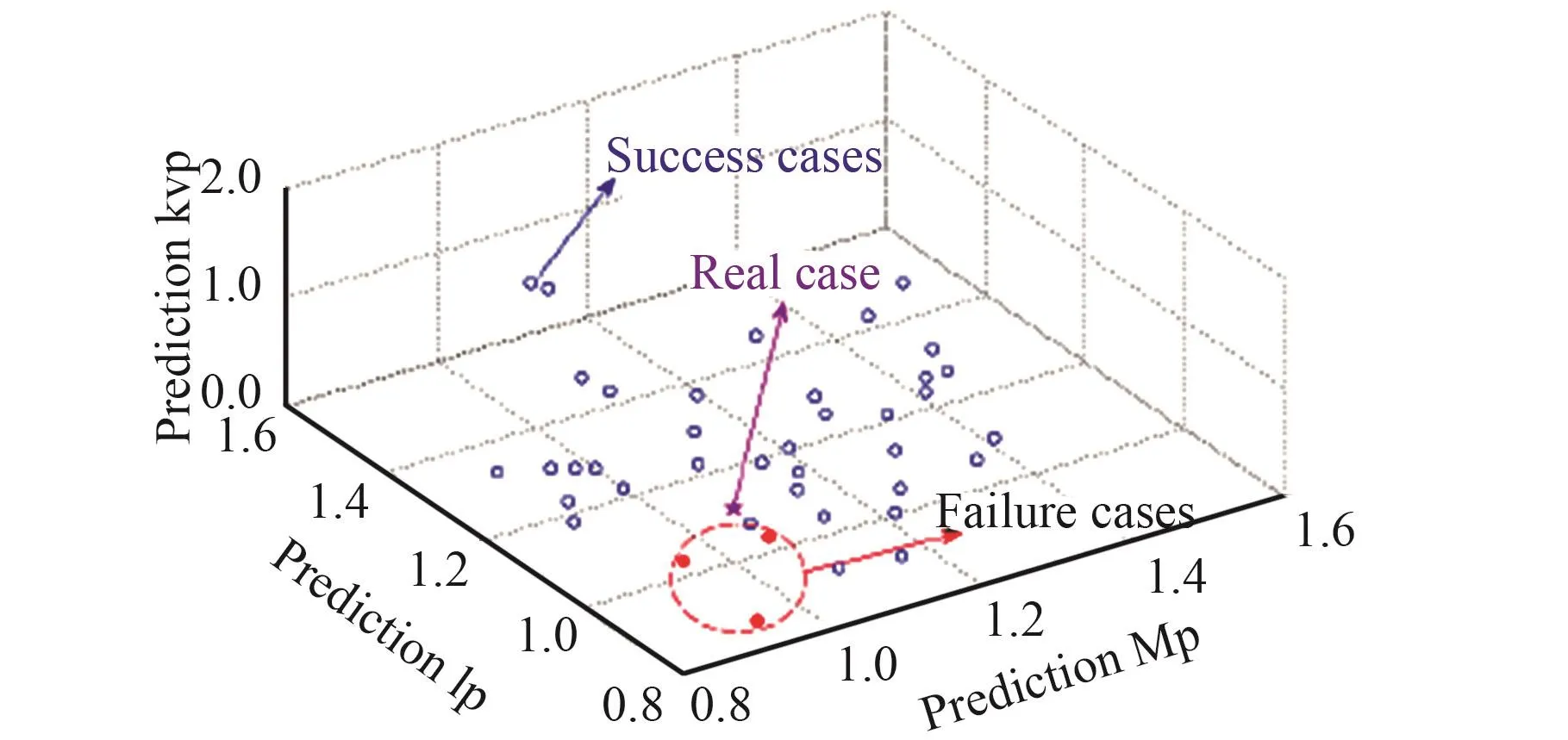
图7 40组随机预测参数的分布Fig.7 The distribution of 40 sets of random prediction parameters

4 基于神经网络的参数识别

在40组实验中去除点3组失败案例，由剩下的37组组成训练集。基于分析图7中37组随机预测参数下的数值模拟，可知每种情况的转矩轨迹取决于预测参数的变化。非线性动态系统之间存在关系，但通过数学方法得到两者之间的关系非常困难，因此数据驱动方法成为一种选择。

4.1 神经网络训练

构建训练集以反映控制器性能与预测误差之间的关系。根据控制策略，每个步骤中的平转矩轨迹应表现出小的预测误差，但性能误差是由线性化和预测误差引起，因此，考虑≈ sinθ以排除线性化误差的影响。如图8所示，当 -0.05≤θ≤0.05，如果没有预测误差，控制输入的θ的变化轨迹应近似为未知常数值(即·u(θ)=0)，否则性能误差完全来自预测误差。因此，可以根据多组数值仿真中的结果提取的·u(θ)轨迹来预测物理参数。

用Levenberg-Marquardt算法训练人工神经网络(ANN)，使用Matlab的神经网络工具箱。神经网络的结构和训练参数如图9所示。

构建训练集的流程图如图10所示。对于每一次成功的模拟，获取 -0.05≤θ≤0.05时(θ)的θ变化轨迹，接着通过二次曲线拟合轨迹(θ)=aθ2+bθ+c， 并将二次曲线的参数记录为具有随机预测参数的训练集，因此，可以通过设置a=b=c=0(轨迹u·θ()=0)来预测物理参数。

图8 通过一步的uθ()轨迹预测物理参数的方法Fig.8 The method of predicting physical parameters through the trajectory of uθ()in one step

训练数据集由37个训练模式组成，其中下标j是索引号。输入向量和输出向量如式(13)所示。

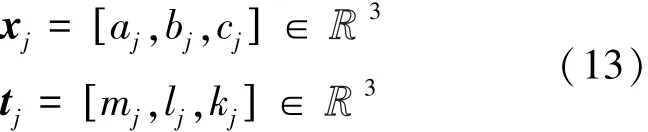
图9 神经网络的体系结构和训练参数Fig.9 The architecture of the neural network and the training parameters

参数辨识的神经网络的设计过程如下：

1)一定范围内，在37组随机物理参数[m，l，k]下进行模拟。

2)在每次模拟中，当-0.05≤θ≤0.05时，u·θ()的θ变化轨迹被获取以及拟合并通过二次曲线拟合以获得系数参数[a，b，c]；

3)构建整个训练集。曲线拟合参数[a，b，c]被指定为输入，而物理参数[m，l，k]被指定为神经网络的输出。

4)训练并建立神经网络，计算a=b=c=0的解作为预测参数。

通过这种方法，预测误差大大降低，但由于不能完全消除线性化的影响，误差不能达到0。

4.2 参数辨识结果

图10 训练集建立流程图Fig.10 Flow chart for building training sets

物理参数的实际值、预测和相对误差如表4所示，人工神经网络训练过程的训练集、验证集及测试集的均方根误差曲线如图11所示。当训练到第21个epoch时，验证集的误差不再下降，结果收敛，此时训练的网络即为最优网络。图12分别表征了训练集、验证集、测试集及全部数据的预测值和真实值的散点图和回归曲线图。预测值和真实值的相关系数在训练集上为0.998，在测试集上为0.941。通过训练，预测参数接近于真实物理参数，平均误差约为1.1%。利用预测的物理参数下进行了数值仿真模拟，运动过程中的扭矩曲线如图13所示，运动过程中扭矩变化较为平稳。

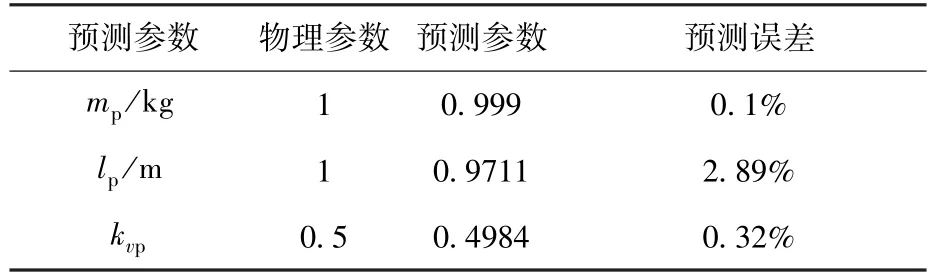
表4 通过人工神经网络预测参数Table 4 Parameters predicted by ANN

5 结论

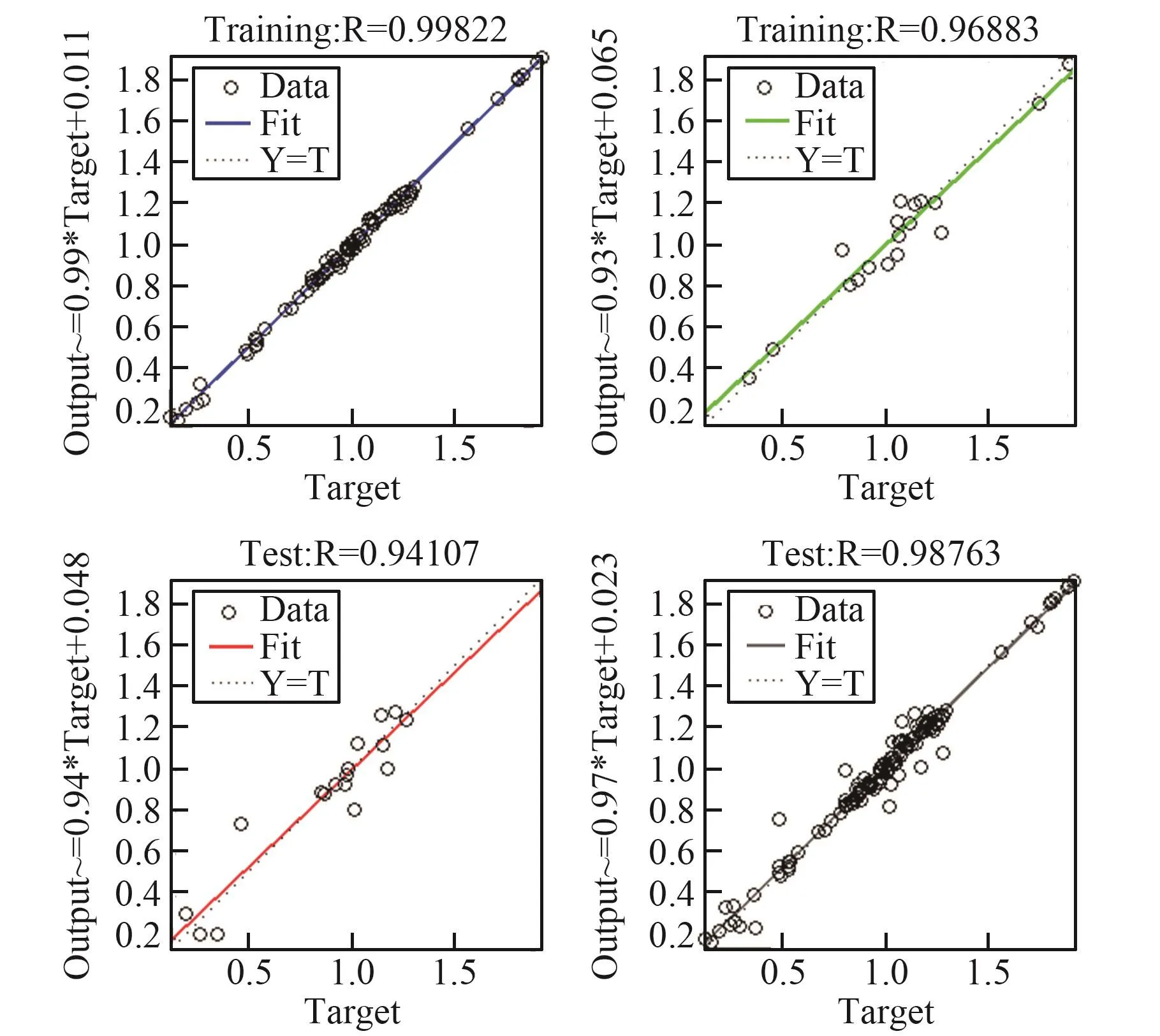
图12 关于训练验证和测试集的线性回归图Fig.12 The linear regression plot for training validation and test sets

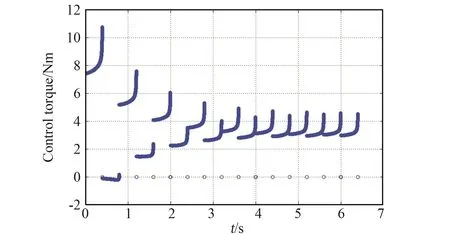
图13 利用预测物理参数所生成的目标速度控制的仿真模拟的转矩轨迹Fig.13 Torque input of simulation for speed control under predicted parameters

本文提出了一种基于控制误差来优化物理参数辨识误差，从而优化控制系统的双足机器人循环优化控制策略。首先，设计了主动组合无框轮动力学运动模型，并提出了一种基于模型的反馈控制器来生成目标速度的有限循环行走。其次，通过使用各种预测参数在数值模拟上验证了该控制器的鲁棒性，并分析由辨识参数误差所产生的控制轨迹误差特性。最后，利用神经网络对37组随机控制轨迹误差特性进行分析，从而开展主动组合无框轮的运动参数识别，预测的平均误差约为1.1%。本文开发的反馈控制器可以克服参数辨识误差实现目标速度控制，并在运动过程中优化参数辨识误差，为运动控制与参数辨识领域提供新思路。