参数不确定机器人关节特征建模与自适应控制研究

张世俊，邢 琰，2*

(1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190)

1 引言

未来，人类对月球、火星等地外星体的探测任务将逐步从星体表面巡视探测向资源开发利用、基地建设等方向发展[1-2]。移动机器人平台是实现地外天体表面巡视探测、辅助人员作业的有效工具。与轮式和履带式运动方式相比，足式机器人的环境适应能力更好，但其结构复杂，对控制的要求比较高[3]。

足式机器人腿部关节控制作为底层控制模块需要较高的控制精度，是机器人运动控制的基础。机器人单腿动力学模型具有多输入多输出、时变、耦合和非线性等特点[4-6]。此外实际机器人较难建立准确的动力学模型，主要有以下两方面的原因：①多功能、可重构机器人的负载、形态的变化导致系统质量特性在工作时发生变化，系统惯性参数难以准确获得；②由于足式机器人的腿在摆动相和支撑相之间交替切换，足地接触力也在实时变化，较难获取系统精确的动力学参数。直接针对腿部动力学模型设计PD控制器是较为经典的方法，因其良好的控制效果和简单易实现的特点，广泛应用于机器人的关节控制，但其参数整定过程比较困难，且对系统参数变化的自适应能力不佳。动力学的耦合特性会影响机器人各关节的控制精度，在高精度控制时需要进行解耦控制。一般解耦控制是通过设计一个解耦网络，将多输入多输出耦合系统解耦为多个单输入单输出的独立系统[7-8]，但需要已知精确的动力学模型。Nikolaou等[9]将人工智能思想用于解耦控制器的设计，并专门讨论了模型不确定性对解耦性能的影响。但基于神经网络的智能算法具有计算量大的缺点，影响了其在航天任务中的应用。因此有必要进一步研究参数不确定情况下的关节控制问题，寻求一种易于工程实现的建模与控制方法。

基于特征模型的自适应控制是吴宏鑫提出的一套实用性很强的自适应控制理论和方法。特征模型是指将对象动力学特征、环境特征和控制性能要求相结合建立的模型[10-11]，与原动力学方程相比，具有形式简单、工程实现容易等优点。基于特征模型的自适应控制方法一般采用离散设计方法，算法简单、适应性和鲁棒性强，主要包括黄金分割自适应控制律、逻辑微分控制律和维持跟踪控制律等控制方法[12-14]，每次设计根据被控对象控制要求选取合适的控制律。该方法经过多年的发展已经在交会对接、飞船返回等领域取得了成功的应用[12]。

本文将基于特征模型的自适应控制方法引入足式机器人腿部关节控制。首先针对足式机器人原动力学模型参数不确定、耦合非线性的特点，建立并推导一种输入解耦的多输入多输出特征模型，以求在保留原系统模型输入输出整体完整性的前提下，充分考虑结构的耦合特点。进而针对该特征模型设计全系数自适应控制器，并仿真验证该方法的有效性。

2 单腿特征建模

一般对于足式机器人来说，腿部质量与身体质量相比很小，并且当机器人行走平稳时躯干姿态波动小，因此在设计腿部关节控制器时忽略躯干运动对腿部的影响，这时腿部动力学模型可大大简化。假设足式机器人单腿具有n个关节，采用Euler-Lagrange方程[4]建立动力学模型如式(1)：

一般来说，实际的机器人可以假设足地作用力有界、关节跟踪指令函数及其一阶和二阶导数有界，则有F′有界，D′(~q)、C′(~q，~q·)、G′(~q)同样满足式(2)～(4)。

其中， A1(t)=C′(Y(t)，Y·(t))，W(t)=F′-G′(~q)+(I-D′(~q))~q¨， 本文若无特别说明 I代表n阶单位阵。同样对于实际的机器人系统，一般可假设关节力矩、关节角度、关节角速度和关节角加速度有界，进而由式(2)～(4)可知，A1(t)和W(t)中的每个元素有界。

对式(6)进行离散化处理，采用欧拉离散化方法，采样周期为T，整理后得式(7)：

其中： F′1(k)=2I-A1(k)T，F′2(k)=-IA1(k)T， G′0(k)=T2I，E′(k)=T2W(k)。 将式(7)写成每一通道的形式如式(8)：

其中 j=1、…、n，f′1，ji(k)、f′2，ji(k) 和 g′0j(k) 分别为 F′1(k)、F′2(k) 和G′0(k) 中的第 i行第 j列个元素。将e′j(k)项压缩至特征参量中，定义如式(9)所示的压缩函数[16]：

其中 j=1、…、n，f1，ji(k)=f′1，ji(k) +S1(k)e′j(k)s1，ji(k) ，f2，ji(k) = f′2，ji(k) + S1(k)e′j(k)s2，ji(k)，g0j(k)=g′0j(k)，ej(k)=e′j(k)sm+13，j。 易知0＜|s3，j|＜1，因此存在足够大的m ＞0使得建模误差ej(k)足够小，从而可以忽略建模误差ej(k)，得到具有输入解耦形式的特征模型如式(11)：

其中Y(k)=[y1(k)…yn(k)]T代表跟踪误差向量，U(k)=[u1(k)…un(k)]T为输入向量，系数具有如下性质：

1)F1(k)和 F2(k)分别是以 f1，ij(k)和f2，ij(k)为元素的正方阵，G0(k)是以g0j(k)为元素的对角阵，其中 i、j=1、…、n。

2)当采样周期确定、机器人腿部工作范围已知时，可估算特征参量的取值范围。对于任意的k≥0，特征参量均在一定的范围内变化，该范围与系统的采样周期相关，如式(12)：

其中集合Ds为如下闭凸集：

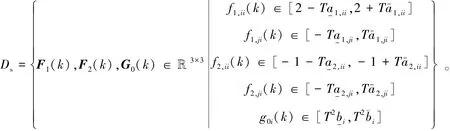
其中i、j=1、…、n，；¯ak，ij＞a-k，ij＞0，¯bi＞b-i＞0，k=1，2，i、j=1、…、n 为定常参数。 由上式可知，当采样周期 T→0 时，有 f1，ii(k) →2，f1，ji(k) →0，f2，ii(k) →-1，f2，ji(k) → 0，g0j(k) → 0， 其中 i、j=1、…、n，i≠ j。

3 多变量全系数自适应控制器

针对建立的多变量特征模型式(11)，采用多变量黄金分割自适应控制律，同时为改善系动态过程增加逻辑微分控制。多变量黄金分割自适应控制律如式(13)所示[10]：

其中l1=(3- 5)/2、l2=(5-1)/2为黄金分割比；Λ为对角常数阵；^F1(k)、^F2(k)、G^(k)为特征模型式(11)的系数估计矩阵，其中各元素由下述投影梯度算法给出。

多变量特征模型的系数可按每一通道单独进行参数估计，将式(11)重写为每一通道形式，得单通道特征模型式(14)：

其中 j=1、…、n，φj(k-1)=[y1(k-1)…yn(k-1)y1(k-2)…yn(k-2)uj(k-1)]T，^θj(k)=[^f1，j1(k)…^f1，jn(k)^f2，j1(k)…^f2，jn(k)^g0j(k)]T。 采用如式(15)所示投影梯度算法[12]。

其中λ1、λ2为正常数，π[x]表示x到有界闭凸集Ds上的正交投影。

逻辑微分控制如式(16)所示：

总的全系数自适应控制律如式(17)所示：

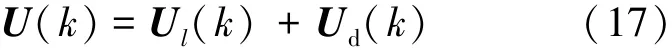
4 仿真验证

为验证本文所建特征模型及控制器设计的正确性，本文以四足机器人为例，对本文方法与基于原动力学模型的经典PD控制方法进行对比。仿真时假定机器人质量、惯量参数和足地接触力未知，PD控制利用关节角度和角速度的测量信息，本文控制方法仅利用关节角度的测量信息。

采用ADAMS和SIMULINK联合仿真技术进行虚拟样机仿真，如图1所示，设机器人总质量200 kg，大腿长0.4 m，小腿长0.3 m。规划机器人以对角步态前进，基于机器人足端工作空间和预期前进速度，设定步态参数如下[17]：机器人行走高度保持为0.8 m，步态周期为0.72 s，直行迈步步长为0.2 m。采用具有复合摆线形式的足端轨迹[18]，迈腿高度为0.1 m。

图1 四足机器人ADAMS模型Fig.1 Model of the quadruped robot in ADAMS

两个步态周期内的髋关节与膝关节曲线如图2、图3所示，图中点线代表关节角跟踪指令，仿真中由步态规划程序给出，实线代表采用全系数自适应控制方法时的实际关节角曲线，点划线代表采用PD控制时的实际关节角曲线。图4为根关节坐标系下一个步态周期内足端轨迹曲线，同样点线代表期望足端轨迹，实线代表采用全系数自适应控制方法时的足端轨迹，点划线代表采用PD控制时的足端轨迹，图中上方的复合摆线表示腿处于摆动相，下方的直线表示腿处于支撑相，支撑相与摆动相切换时具有较大的跟踪误差，这是由摆动腿触地是与地面发生碰撞，足地接触力产生突变造成的。

图2 左前腿髋关节角度曲线Fig.2 Angle curves of hip joint in left foreleg

为进一步验证特征建模及自适应控制器对不同对象参数的控制效果，假设机器人三足支撑站立，修改另一条腿足端质量为10 kg，令其跟踪与上一仿真相同期望轨迹。2个周期内的髋关节与膝关节曲线如图5、6所示，图中点线代表关节角跟踪指令，实线代表采用全系数自适应控制方法时的实际关节角曲线，点划线代表采用PD控制时的实际关节角曲线。图7为足端轨迹曲线，同样点线代表期望足端轨迹，实线代表采用全系数自适应控制方法时的足端轨迹，点划线代表采用PD控制时的足端轨迹。

图3 左前腿膝关节角度曲线Fig.3 Angle curves of knee joint in left foreleg

图4 左前腿足端轨迹Fig.4 Foot trajectory of left foreleg

图5 负载时左前腿髋关节角度曲线Fig.5 Angle curves of hip joint in left foreleg under load

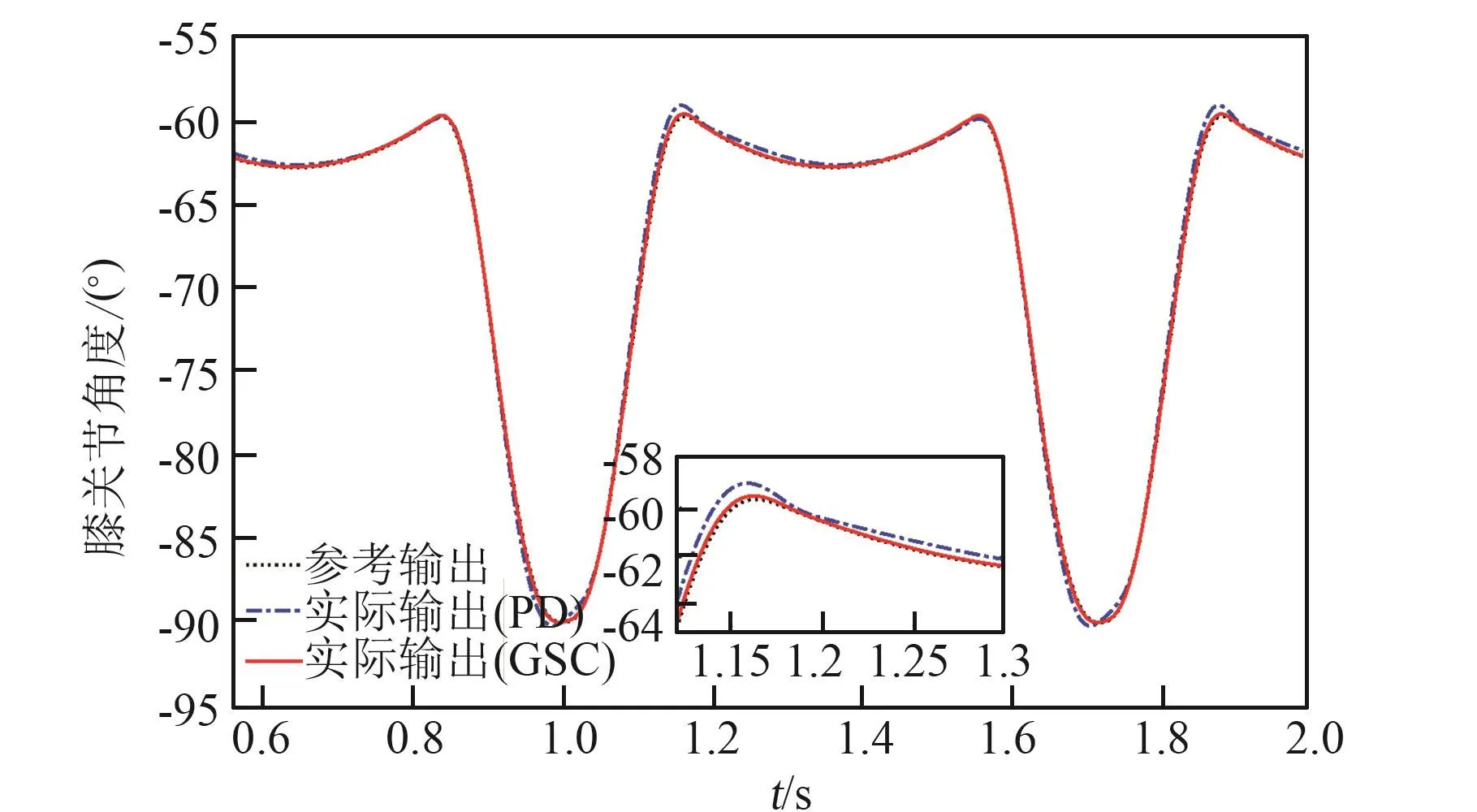
图6 负载时左前腿膝关节角度曲线Fig.6 Angle curves of knee joint in left foreleg under load

图7 负载时左前腿足端轨迹Fig.7 Foot trajectory of left foreleg under load

仿真时足端负载质量未知，由仿真曲线可知，本文的特征建模及全系数自适应控制方法对模型参数的不确定性具有较好的自适应能力。

5 总结

本文将特征建模和全系数自适应控制方法用于足式机器人关节控制，由仿真结果可知本文的方法具有较好的控制效果，同时对模型参数不确定性有自适应能力，可作为为足式机器人关节建模和控制问题的一种解决方案。本文未涉及闭环系统的稳定性分析。