不同条件对纤维素糖化反应动力学参数的影响

刘 璐， 张志才*，2， 樊亚娟， 胡坤雅， 汪 佳

（1.江苏大学，农业生产加工工程研究所，江苏 镇江 212013；2.北京绿科天成生物有限公司，北京 102300）

秸秆转变成生物质能源包括4个步骤：秸秆的预处理、秸秆纤维素的糖化、发酵和生物能源的提取。其中纤维素糖化，即把秸秆中的纤维素转变成可发酵的己糖[1-3]，是秸秆开发利用生产清洁能源过程中一个极其重要步骤。秸秆中的纤维素糖化反应是一个动态反应过程，为探究其行为机理需要进行动力模型学研究，利用该模型研究影响酶水解效率的因素及规律[4]。

由于纤维素酶水解过程是异相反应，且反应速率常数不断降低，准稳态理论不成立，再加上酶水解反应动力学较复杂，不能采用传统的米氏方程进行描述[5]。而米氏方程模型仅适用于均相体系中，许多生物催化反应发生在非均相系统中，受到扩散与传质，反应物分子、产物分子与催化剂表面发生的吸附、传递、脱附、酶变性等影响[6-7]。因此，无法用传统的米氏方程理论描述非常规的反应[8]，需要对模型进行修改以描述非均质系统中的酶反应[9]。

Kopelman等认为非均相反应的动力学不遵从经典动力学模型，速率常数随着时间而变，速率常数与反应级数和谱维数有关，酶解反应动力学属于类分形动力学模型[10-11]。Priit Väljamäe采用类分形动力学研究了里氏木霉的水解过程，同时提出类分形动力学可能也适用于纤维素的酶解过程[12]。Huang研究了不同浓度的不溶性酶对不同浓度的底物水解，提出了快速吸附的动力学模型，并讨论了确定动力学参数的方法[13]。

而IMM的研究对象是复杂、抽象和未简化的非线性系统，不仅可以认识其内在规律、反映事物的内在本质，还可以简化研究过程。简化的动力学模型使用Kobs，0来考虑预处理前后底物酶的初始活性和可及性，Ki表现出由酶对惰性和非反应性物质的阻碍反应引起的酶活性逐渐丧失的异构系统，IMM可以清晰反应纤维素酶水解的反应过程。对此，作者选择IMM研究了不同反应条件对纤维素糖化反应动力学参数的影响，以获得最大糖得率，为木质纤维素的糖化奠定良好的基础。

1 材料与方法

1.1 材料

纤维素：购自上海阿拉丁生化科技股份有限公司；纤维素酶：购自和氏璧生物技术有限公司。

1.2 动力学模型

纤维素的糖化反应发生于非均相体系，反应过程可以用下列方程表示：

其中S，P和ES分别表示底物、产物，和酶-底物复合物。k1和k2是指正向反应速率常数，k-1表示反向反应速率常数。模型假设：（i）与酶反应相比，固体底物对酶的吸附速率更快，（ii）酶的反应受阻主要包括产物抑制，基质对酶非反应位点的吸附作用，以及酶的质量转移阻力，（iii）酶反应被认为是酶（E）与底物的结合形成酶-底物复合物，（iv）预处理对固体底物结构的影响通过相应的反应速率即k1，k-1和k2反映出来。基于以上假设，在反应过程中，当[ES]处于准稳态，对于[ES]有，μ分解=μ合成，μ分解=（k-1+k2）[ES]，μ合成=k1[E][S]，由此得到[ES]=[E][S]/Km，这里Km=（k-1+k2）/k1。 因此，产物的生成速率可以表示为：

产物和底物达到平衡时，

式（2）中：[S0]表示底物初始浓度。 因为[ES]＜＜[P]+[S]，所以[ES]可忽略。 （2）可简化为下式：

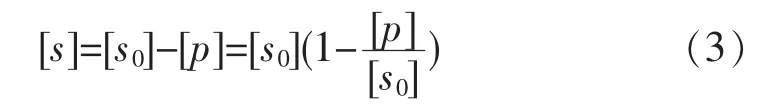
公式（3）代入公式（1），化简得到下列公式（4）：

令[P]/[S0]=Ytrs，代入式（4）中。

公式（5）中k2[E0]/Km=Kobs，0，且Kobs，0取决于底物预处理的效果，酶对底物的可及性以及酶在固体基质中的活性。非均相反应体系中的糖化反应由于底物的不可溶解性导致酶与底物接触面积过小而使得反应速率很慢。因此，酶的活性受到阻碍，酶的水解速率逐渐减小。阻碍的反应可由下式表示出来，其中，Ki表示水解过程中无效酶的系数，Ei表示无效酶。阻碍反应可通过如下一阶方程表示：

随着反应的进行，可与酶反应的底物随着时间的增大而减少。基于对实验的观察，Ki可用随时间变化的下列函数表示：

酶的物料平衡组成为：

式（8）中，[E0]，[E]，[ES]，[Ei]指初始酶浓度，自由酶的浓度，一个酶-底物复合物的浓度，一个无效酶的浓度。 式（8）对时间求导，得式（9）。

因为[ES]复合物被假设为稳定态且d[ES]/dt≈0，所以，式（9）可被简化为下式。

将公式（7）带入公式（10）中，得下式。

公式（11）进行积分，得[E]/[E0]=1/（1+αt）2，带入式（5），得下式。

对公式（12）整理并积分给出下列公式。

对式（13）进行变形，得下式。

式（14）中，两边同时被t除，得到的t项和常数项系数分别为 α/Kobs，0和 1/Kobs，0，Ki可由式（7）进行计算，预测的Ytrs（Ytrs，pred）可由下式计算。

1.3 试验设计

由试验得到条件温度、pH、底物质量浓度和酶质量浓度对糖得率影响最大，因此设计4因素3水平的29组的Box-Behnken试验，研究温度（A）、pH（B）、底物质量浓度（C）和纤维素酶质量浓度（D）对糖得率Ytrs的影响，并采用Design Expert 8.0.1、SPSS 17.0软件进行分析[14-17]，通过比对各因素显著性筛选出最适合水解的条件，每组试验重复3次，试验因素及水平见表1。对试验结果进行回归分析、方差分析。

为了探究Ytrs与Kobs，0、Ki相关性， 利用 SPSS 17.0软件对其进行分析，通过显著性判断因素之间是否相关，获得方程，并解出方程，讨论三者之间的关系，获得最大糖得率。

表1 Box-Behnken设计方案Table 1 Box-Behnken design of response surface design

1.4 分析方法

1.4.1 纤维素酶水解将纤维素与纤维素酶在pH 4.8 0.1 mol/L的乙酸盐缓冲液混合后，加到100 mL三角瓶中用DNS法[18]测定初始还原糖质量浓度为C0。在50℃，120 r/min水浴摇床中的振荡糖化，分别于 0、1、2、4、8、16、32 h 取样，并将样品冰浴冷却。取样品与离心管中，4 000 r/min离心15 min，取上清液测定还原糖含量和酶活。

1.4.2 还原糖的测定采用3，5-二硝基水杨酸法[19]。

总还原糖的产量（Ytrs）根据下列公式计算：

其中，V为反应体系的体积（mL），G为底物质量（g），C0、C1分别为反应前后还原糖质量浓度（g/mL）。

所有试验均经过3次平行试验，结果以平均值来表示。

1.5 数据处理

所有试验均经过3次平行试验，结果以平均值来表示，试验结果采用EXCEL 2007和SPSS 17.0统计分析软件来处理。

2 结果与讨论

2.1 模型拟合结果分析

影响酶反应速率的因素主要包括反应温度、溶液的pH、酶质量分数和基质质量分数。试验选择响应面分析研究了这些因素的单独作用和交互作用对酶反应速率的影响。4因素3水平29组试验的BBD运行，反应不同时间还原糖得率的结果显示在表2。

表2 Box-Behnken设计运行结果Table 2 Run results of Box-Behnken design of response surface design

用IMM模型 （公式14）拟合表3中的试验数据，得到表3。

从表3可以看出，所有拟合的R2都高于0.96，并且与adj-R2值极其接近，p＜0.001，说明IMM模型能很好的拟合实验结果，而且具有较高的解释率和可信度。通过拟合的方程得到的Kobs，0和Ki也显示在表4。

表3 Box-Behnken设计运行结果的模型拟合分析Table 3 Model fitting analysis of the run results of Box-Behnken design of response surface design

2.2 响应面结果分析

从表3可见，反应时间32 h的糖得率最高，因此试验选择 32 h 的糖得率（Ytrs）和表 4 中的Kobs，0和Ki作为响应值，分析了反应温度，pH，底物质量浓度和纤维素酶质量浓度单独作用和交互作用对这3个响应值的影响。采用下列方程拟合实验数据：

其中Y是预测响应值（Ytrs，Kobs，0和Ki）；β0是常数；βi是单独作用系数；βij是不同因素间XiXj交互作用系数，βii同一因素之间交互作用系数；Xi和Xj表示自变量值。拟合结果显示在表5。

方差分析的结果如表5所示。四元二次模型的p＜ 0.05，Ytrs值，Kobs，0和Ki的F值分别为15.52，9.65和3.03，表明模型非常显著。模型的失拟项“Prob ＞F”值分别为 0.054 3，0.856 6，0.052 6 均大于0.05，即失拟项不显著，因此模型具有统计意义。将表5中的各项系数分别带入方程（17），得到下列方程：

表4 二次响应面模型的方差分析Table 4 ANOVA analysis for quadratic response surface

采用Design Expert 8.0.1软件对试验结果进行分析。模型的“Prob＞F”的p值小于0.000 1，表明模型是显著的。在响应值为Ytrs的模型中，显著项为B，C，D，CD，A2，B2，C2， 在响应值为Kobs，0的模型中，显著项为A，C，D，在响应值为Ki的模型中，显著项为A，A2，B2。因此响应值为Ytrs模型中包含两个线性项（B，C，D），一个交互项（CD），三个交互项（A，B和C）； 响应值为Kobs，0模型包含两个线性项（A，C，D）；响应值为Ki模型包含两个线性项（A），和两个二次项（A2，B2）。

2.3 单因素作用分析

2.3.1 温度对反应动力学模型参数的作用纤维素酶水解是一种化学反应，以分子运动为基础，以酶分子与底物分子的吸附、络合和解离为基础，分子动能与温度直接相关，且酶是生物催化剂，具有温度效应，影响酶解率[20]。在40～48℃之间，温度升高，糖得率逐渐增大，无效酶（Ki）逐渐降低，在48℃时，获得最大糖得率和最低的无效酶；当温度超过48℃时，酶以失活为主无效酶逐渐增大，糖得率逐渐降低。在整个试验温度范围内随着温度升高，Kobs，0一直保持增加趋势，说明增加温度有利于增加酶与底物的可及性，提高酶的利用率。多数研究显示，纤维素酶作用底物的最佳温度范围为 40～65℃[21]，与实验所得结论一致。

2.3.2 pH对反应动力学模型参数的作用酶在一定的pH范围内才具有较高的催化活性，因此糖得率随pH变化的曲线呈抛物线形状。当pH＜4.5时，随pH值增加，糖得率逐渐增加，而无效酶逐渐减少；当pH=4.5时，糖得率取得最大值，而无效酶取得最低值；当pH＞4.5，纤维素酶变性，较高的pH值会破会酶的空间结构，影响酶活性部分的解离状态，因此随着pH升高，虽然会保持蛋白质的天然性质，却失去了应有的活性[22]，导致无效酶活性增加，因此糖得率也随之减少。在pH在4.5时，糖得率取得最大值和无效酶取得最低值，证明pH的变化，通过影响纤维素酶的活力实现。在整个试验pH范围内随着pH升高，Kobs，0一直保持增加趋势，说明增加pH有利于增加酶与底物的可及性，提高酶的利用率。研究显示，最适 pH值范围为 4.0～5.5。

2.3.3 底物质量浓度对反应动力学模型参数的作用增加底物质量浓度，尽管增加了酶与底物总的可接性，但是对于单位质量的底物来说，其相对可接性（Kobs）是变小了，同时由于底物质量浓度增加，单位质量的酶失活作用（Ki）也表现的减少，因此导致单位底物的糖得率降低。当底物质量浓度较低，吸附到底物上的酶较少，大多数酶成游离状态，底物处于饱和吸附状态，因此当底物质量浓度增加，酶的可接性增加，底物吸附酶总量增加，但是单位重量的底物吸附的酶量减少，因而总的还原糖得率也降低。底物质量浓度增加，酶与底物的接触面积越大，酶解率提高。已有研究证明酶催化反应不是底物质量浓度越高越好，底物质量浓度越高，意味着酶溶液体积相对变小，造成反应产物不易扩散，会抑制酶的水解，严重降低水解速率。

2.3.4 酶质量浓度对反应动力学模型参数的作用在一定酶质量浓度范围内，随着酶质量浓度的增加，增加底物质量浓度，可以增加单位底物酶可接性，因此在整个试验范围内，随着酶质量浓度增加，Kobs，0逐渐增加，酶质量浓度增多，导致酶非反应位点之间的吸附以及游离酶的增加，即单位底物无效酶（Ki）含量也在逐渐增加。因此随着酶质量浓度增加，糖得率增加是由于单位底物的酶可接近性增加产生。许多文献报道纤维素分子能和酶分子的结合点数有限，当这些结合点全部被酶分子占据后，再增加纤维素用量，起不到酶解作用。

2.4 交互作用分析

在响应面分析中，等高线通常用于研究各种因素之间的交互作用，分析等高线图，可以获得最优响应值时各因素的取值。表5显示，只有CD（酶溶度和底物浓度）交互作用达到显著水平，说明其对糖得率影响显著。因此分析了这两个因素的交互作用。图1显示在实验范围内，酶质量浓度越高，底物质量浓度越低，其糖得率越高。该结果与单因素实验结果一致。

通过对回归方程18，19和20求解，得到获得最大Ytrs的条件为：pH 4.4，水解温度47℃，纤维素酶质量浓度为3 g/dL，底物质量分数5%。预测最大糖得率为0.485 4。可获得最大Kobs，0的条件为：pH 7，水解温度60 ℃，纤维素酶质量浓度为3% ，底物质量浓度5 g/dL。 预测最大Kobs，0为 0.474 0 h-1。 可获得最小Ki值的条件为：pH 4.47，水解温度47.40 ℃，纤维素酶质量浓度为1 g/dL，底物质量浓度5 g/dL，预测最小Ki值为0.055 8 h-1。综上所述，获得最大Ytrs，Kobs，0最小Ki的最优条件为：pH 4.84， 温度48.9 ℃，纤维素酶质量浓度3 g/dL，底物质量浓度5 g/dL。

图1 酶质量浓度和底物质量浓度对糖得率影响的响应面等高线图Fig.1 Response surface plot combined effects of Enzyme concentration and Substrate concentration ratio on Sugar yield

2.5 Ytrs，Kobs，0 和 Ki的关系分析

因为Kobs，0等于k2[E0]/Km，[E0]是纤维素酶初始浓度，在实验中是常数，Kobs，0与k2[E0]/Km成比例。k2是从酶-底物复合物到最终产物正向反应的速率常数。k2越大，Ytrs越大。米氏常数Km越小，亲和力越大。因此，可以推断Ytrs与Kobs，0呈正相关。Ki是水解反应期间无效酶的系数，因此较低的Ki表示较少的无效酶和更多的有效酶。因此，Ytrs与Ki是负相关。为了验证这两个推导，以表3中32小时糖得率为因变量，表4中的kobs，0和Ki为自变量，采用下列方程（21）进行非线性回归分析：

其中，a，b，c和d分别为（Kobs，0）2，Kobs，0，（Ki）2和Ki的系数，e为常数。表 5显示F试验的F值（68.304）和t检验的p值（0.000）表明Ytrs与Kobs，0、Ki相关性非常显著，分析的可信度极高。R2为0.919，高于R2为0.80的置信度[27]，以上均表明本模型的可预测性相对更可靠。调整R2为0.906，接近R2值，即模型具有良好适应性。

表6所有参数的系数均非常显著（p=0.000）。其中（Kobs，0）2和（Ki）2的系数为负值证明Ytrs和Kobs，0或Ytrs和Ki的关系曲线呈现倒U形，Ytrs具有最大值。在将表5中的每项的系数引入等式（21）之后，得下式。

分别对Kobs，0、Ki求导得式（23）、（24）

令Ytrs′=0，Kobs，0=0.450 9 和Ki=0.053 8。 当Kobs，0＜0.450 9，Ki＜ 0.053 8 时，Ytrs′＞ 0，即Ytrs与Kobs，0和Ki显著正相关。 相反，Kobs，0＞ 0.450 9 和Ki＞ 0.053 8，Ytrs′＜ 0， 即Ytrs与Kobs，0和Ki显著负相关。 当Kobs，0=0.450 9，Ki=0.053 8 时，Ytrs达到最大值 0.604 0。 在表中，Kobs，0值大部分小于 0.450 9， 所有Ki值大于0.053 8，因此Ytrs与表征酶的初始活性和酶与底物的可及性的Kobs，0显著正相关，与无效酶的系数Ki显著负相关。

3 结语

对纤维素酶水解动力学进行了研究，建立了简单的动力学模型，响应面设计给出了获得最大Ytrs和Kobs，0以及最小Ki的条件。分析了不同因素在水解过程中对糖得率的影响和各因素之间的交互作用对糖得率的影响。获得最大糖得率的条件为pH 4.41，温度47℃，纤维素酶质量浓度3 g/dL和底物质量浓度5 g/dL。在最优条件下，最大Ytrs为0.4854，与实验所获得最大糖得率的0.442 9接近。温度和pH主要通过改变无效酶系数影响糖得率，而酶和底物质量浓度主要改变酶对底物的可接性作用于糖得率；并进行了糖得率与动力学各参数之间的回归线性分析，得到相关性大于0.9的结果。在试验条件下，Ytrs与Kobs，0正相关，与Ki负相关。