混合连续梁桥主梁钢—混结合段受力性能分析

付涛宋明康郏建树高朝彪

(山东建筑大学交通工程学院，山东济南250101)

0 引言

对于多跨连续梁桥，其边跨一般为中跨的0.6～0.8倍，当采用箱型截面的多跨连续梁时，边孔跨径可以减少为中孔跨径的0.5～0.7倍[1]。对于为满足城市桥梁和跨线桥的交通需求而需要增大中孔跨径的特殊情况，当设计边孔跨径与中孔跨径的比值＜0.5倍时，会在边跨桥台顶端支座处产生较大的负反力，从而限制了桥梁结构的应用[2]。近年来，针对连续梁桥边跨和中跨比值过小而在边跨桥台顶端支座处产生负反力的情况，混合连续梁桥作为一种新型组合结构在国内外得到了广泛的推广和应用，钢—混凝土混合连续梁桥完美结合了2种材料的优点，充分发挥了钢材跨越能力较大和混凝土材料压重作用的特性，使其受力性能、技术经济效益、跨越能力及成桥效果均优于采用单一材料的钢结构或混凝土结构[3]。1996年建成通车的主跨为590 m的上海徐浦大桥，为我国首座采用混合梁结构的斜拉桥；1997年建成公铁两用的主跨为430 m的香港汲水门大桥，为混合梁斜拉桥；而后又相继建成的主跨为618 m的武汉白沙洲长江大桥以及主跨为330 m的连续刚构桥重庆石板坡长江大桥[4]均采用了钢—混凝土混合梁结构形式。混合连续梁桥主梁钢—混结合段构造繁琐且受力复杂[5]，是确保钢与混凝土结合牢固、可靠的重要构件，是混合连续梁桥设计成败的关键[6]。

为了解钢—混结合段受力特点，对其进行受力性能分析，以期为同类结构在实际工程中的应用提供可靠依据。文章以某三跨变截面混合连续梁桥为研究背景，主桥跨径布置为(50+140+50)m，全长为240 m。由于该桥跨越铁路的交通需求，为保证桥下铁路的通行条件，降低主梁建筑高度，需要增加中跨跨径，采用了混合连续梁桥设计方案，边跨与中跨的跨径比值为0.36。大桥中跨中部采用钢箱梁，中跨两侧采用预应力混凝土箱梁，为单箱双室截面，采用现浇C55混凝土，梁高按二次抛物线变化，在位于中跨距离边支座中心线3.8 m处，通过设置钢—混结合段使钢箱梁与混凝土箱梁成为连续结构体系。

1 混合连续梁桥主梁钢—混结合段设计与构造

钢—混结合段是连接钢箱梁与混凝土箱梁的重要结构，是混合梁桥结构中材料和刚度的突变点[7]。钢构件与混凝土构件的受力性能、两者之间力的传递情况、结合面之间的协同工作性能和剪力钉的连接作用是影响钢—混结合段可靠性的重要因素[8]。大桥主梁钢—混结合段采用“PBL剪力键(开孔板连接件)+钢格室”的后承压板构造形式，结合段范围总长为10.7 m，其中钢与混凝土互相咬合段为2 m、钢箱梁过渡段为5.75 m、混凝土过渡段为2.95 m。截面轴力和弯矩通过钢隔室承压板、PBL剪力键及钢板与混凝土的摩擦力传递，剪力和扭矩主要通过结合面端部剪力钉传递。由于钢箱梁与混凝土箱梁的截面特性相差较大，使结合段两侧的刚度变化显著，为了实现刚度过渡的效果，结合段结合面钢箱梁侧过渡段采用带变高度T形加劲肋的U形加劲进行过渡。结合面混凝土梁侧的过渡段采用变化顶、底、腹板的厚度进行刚度过渡，结合段通过钢箱梁加强段与钢箱梁连接。同时在钢主梁与混凝土梁之间设置纵向预应力钢束，使之有良好的整体性，并可以平衡运营期活载效应。另外，混凝土箱梁内的结构钢筋伸入结合段，与PBL板孔内的贯穿钢筋相互绑扎焊接[9]。钢—混结合段构造如图1所示。

该桥在钢—混结合段的顶板、底板及腹板上均设置钢隔室，钢隔室是钢—混结合段的关键部分，钢隔室腹板上开有Φ70 mm圆孔，腹板剪力板上开有Φ80 mm圆孔，并穿过Φ20 mm HRB400钢筋与进入圆孔的混凝土包裹在一起形成PBL剪力键。根据国内外多次剪力键的推出实验研究[10-14]表明:相比抗剪焊接销钉，PBL剪力键具有承载力高、抗疲劳性能好、延性好、方便施工、加工制造简单和造价经济等优点，所以，钢—混结合段采用PBL剪力键在很大程度上改善了结合段的力学性能，将钢箱梁截面上的轴力及弯矩荷载传递到混凝土中去，使钢箱梁截面应力得到分散。

同时，为使钢隔室与混凝土更紧密的结合，在钢隔室与混凝土相贴的顶板、底板和承压板均设置高为80 mm的Φ22 mm电弧螺柱焊用圆柱头焊钉，材质为ML15，承压板上的剪力钉起到竖向抗剪的作用，圆柱头焊钉是目前应用最广泛的抗剪连接件[15]，具有抗剪承载能力高、施工速度快等优点。在格室上角点及适当位置设置排气孔，在下角点预留压浆孔。为保证结合段中混凝土在浇筑时能够自由流动，在钢格室顶板上开设浇注孔，隔板上设置连通孔。

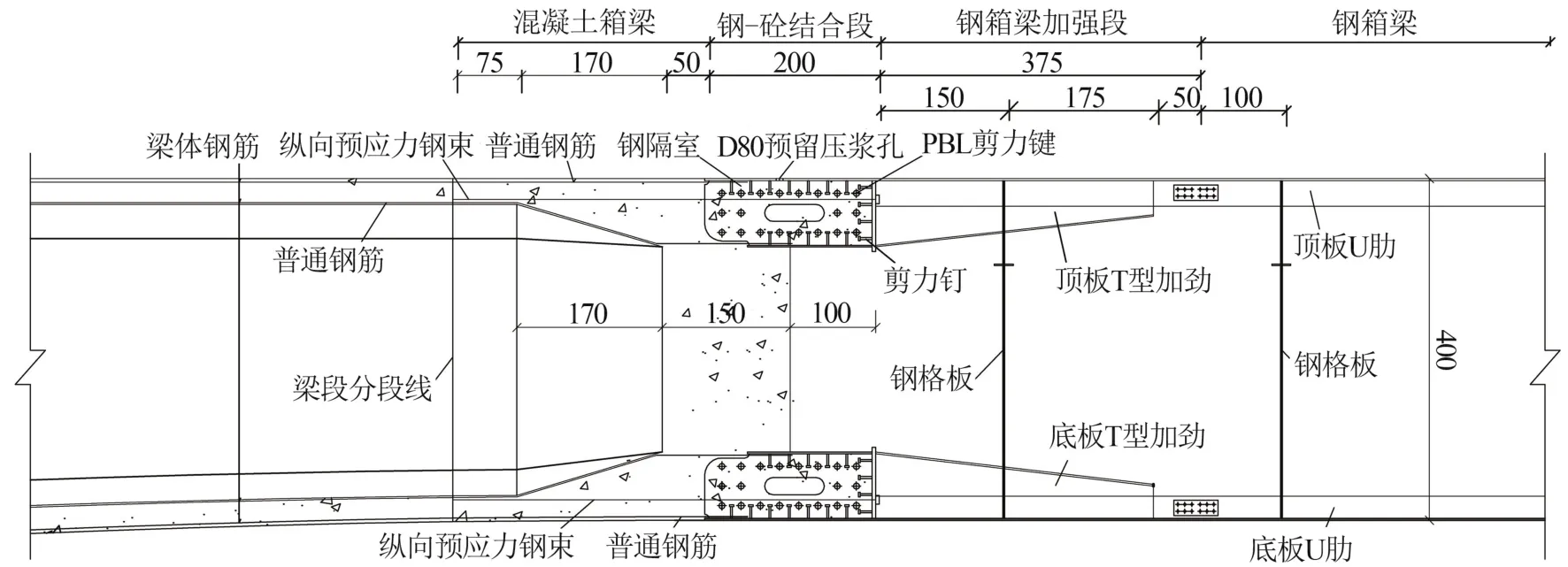
图1 钢—混结合段构造图/cm

2 钢—混结合段局部应力数值分析模型

2.1 计算模型

在保证分析精度的前提下提高计算效率，首先采用Midas/Civil建立全桥的空间杆系有限元模型，分析荷载组合为“恒载+公路Ⅰ级+混凝土收缩+混凝土徐变+支座沉降+温度”，计算大桥在施工阶段及使用阶段的最不利内力，弯矩以截面下缘受拉为正，受压为负；剪力以结构段按顺时针转为正，逆时针转为负；轴力以受拉为正，受压为负；扭矩正负按右手螺旋法则确定。在ANSYS整体坐标系下，计算得到x向剪力、弯矩分别为17.25 kN、94 441 kN·m；y向剪力、扭矩分别为2 368 kN、8 369 kN·m；z向轴力、弯矩分别为-35 098 kN、826 kN·m。

采用ANSYS软件建立钢—混结合段空间板壳和实体单元相结合的有限元计算模型，通过给预应力钢筋施加初始张拉应力，使其作用在结构上，分析弹性体的应力状态。模型中为了尽可能真实的模拟主梁钢—混结合段的受力情况，消除边界条件及加载对结合段的影响，取与其相连接的混凝土箱梁、钢箱梁加强段、钢箱梁和结合段4部分作为计算分析对象，建模全长为 21.7 m，其中混凝土箱梁为9.95 m，钢箱梁加强段为3.75 m，钢箱梁部分为6 m，结合段部分为2 m。

建模过程中，假定结合段部分顶面和底面为刚性，截面变形过程中遵循平截面假定。忽略钢板和混凝土之间的粘结滑移，即钢板与混凝土协同受力和变形，作为结构的安全储备，混凝土与钢板通过PBL剪力键和剪力钉连接受力。建模过程中忽略普通钢筋的影响，只考虑纵向预应力钢束的作用，同时考虑了预应力钢束的应力损失。

2.2 单元的选择与划分

采用ANSYS有限元软件建立实体单元与空间板壳单元相结合的模型，混凝土梁段采用实体单元soild65，该单元具有8个节点，每个节点有3个自由度；钢箱梁桥面板、加劲肋、顶底板、腹板及承压板等钢板构件采用shell63壳单元模拟，单元每个节点有6个自由度；预应力钢束采用link180有限应变杆单元模拟，在承压板壳单元与混凝土实体单元上分别建立节点与其连接；采用combin39非线性弹簧单元模拟PBL剪力键和剪力钉的剪切滑移特性。建模时，混凝土、钢材和预应力钢绞线采用的材料参数见表1。

表1 材料参数表

钢—混结合段有限元模型如图2所示，坐标系与桥向的关系为:x轴沿横桥向、y轴竖直向上、z轴沿桥梁轴向。模型的划分网格采用自由划分的方法，划分时使钢混接触面上的节点相对应，为钢混接触面上的节点连接做准备。网格划分后的计算模型如图2(b)所示，钢—混结合段的有限元计算模型共划分为216 371个单元，其中shell63单元为32 752个、soild65单元为179 057个、link180单元为 54个、combin39单元为4 508个。

2.3 边界条件及荷载施加方式

根据圣维南原理，钢—混结合段的局部应力与离其较远区域的应力联系较小，仅和相近区域的应力状态有关，因此只要在足够远离结合段区域的断面施加相应的内力，其对所研究的结合段区域的局部应力影响可以忽略。

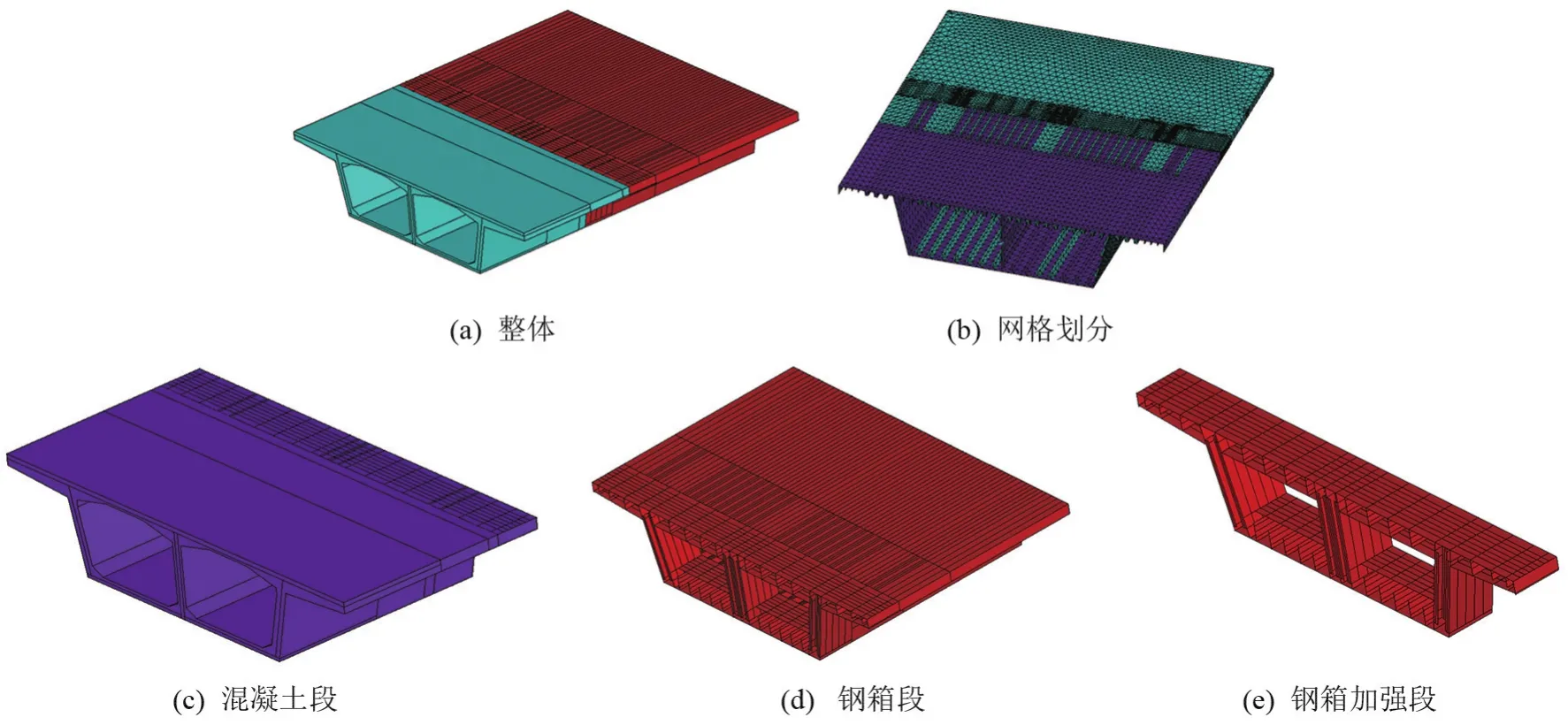
图2 钢—混结合段有限元模型图

应用有限元分析软件Midas/Civil建立全桥杆系模型，进行整体桥梁结构的分析，分别得出钢箱梁与混凝土箱梁在截面处及结合面处的弯矩、剪力、轴力及扭矩。对整体模型的位移和应力分析，且考虑到混凝土箱梁刚度较大，位移较小，故将混凝土梁端所有节点的自由度固定约束，在钢箱梁端不施加任何约束，使模型成为悬臂结构，在钢箱梁远端截面质心处建立一个节点，并将质量单元mass21赋予此节点，将其作为主节点，用CERIG命令将钢箱梁端面上所有从属节点的自由度与主节点的所有转动和平动的自由度进行耦合，将轴力转化为顺桥向节点力，剪力转化为竖向节点力，弯矩先分解成力偶再按等效节点荷载施加于距离混凝土梁端固结截面为21.7 m处的钢箱梁端部节点上，采用此简化方法将其施加到板壳单元实体模型上。荷载则以钢—混结合段各截面上的控制内力组合为依据。

3 模拟结果与分析

3.1 钢—混结合段钢箱梁局部应力

通过有限元程序ANSYS对钢—混结合段进行应力分析，所得结合段钢箱梁应力云图如图3所示，图中拉应力为正，压应力为负。

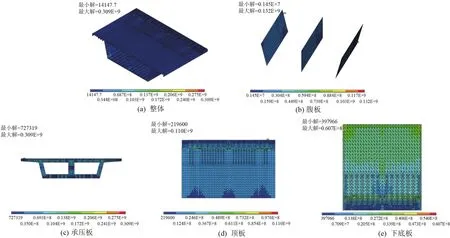
图3 钢—混结合段钢箱梁Mises应力云图/Pa

根据图3分析可知，顶板应力水平较低，最大应力为1.1×108Pa；底板应力水平偏低，最大应力为6.07×107Pa；腹板在承压板位置局部出现应力集中，最大应力为1.32×108Pa，但小于屈服应力2.7×108Pa；承压板只在预应力钢束锚固位置出现应力集中，最大为3.09×108Pa，剔除锚固点，应力均在安全范围内。由上述结果可以看出，除承压板预应力筋锚固位置处应力集中外，钢—混结合段其余位置的钢箱梁各构件均满足要求。

3.2 钢—混结合段混凝土箱梁局部应力

混凝土强度等级为C55，其轴心抗压、抗拉强度设计值分别为 2.44×107、1.89×106Pa。 结合段混凝土箱梁应力云图如图4所示。混凝土箱梁顺桥向正应力最大值为5.19×107Pa，第三主应力最大值为6.78×107Pa，均为剪力钉锚固位置处出现的应力集中现象，剔除局部锚固点，其余应力均在安全范围内；混凝土箱梁横桥向正应力最大值为1.38×107Pa，混凝土箱梁第一主应力最大值为2.99×106Pa，不管是否出现应力集中现象，压应力均在安全范围内。

分析表明，混凝土箱梁除在剪力钉锚固位置处出现应力集中现象外，其余应力均在安全范围内，而在锚固位置处出现的高应力区对结构整体使用的影响较小。

图4 混凝土箱梁应力云图/Pa

3.3 PBL剪力键及剪力钉计算结果

3.3.1 剪力键计算结果

PBL剪力键受力计算结果见表2，最大剪力为52.48 kN，其值＜324.4 kN，表明PBL剪力键最大剪力小于其抗剪承载能力，满足规范要求。

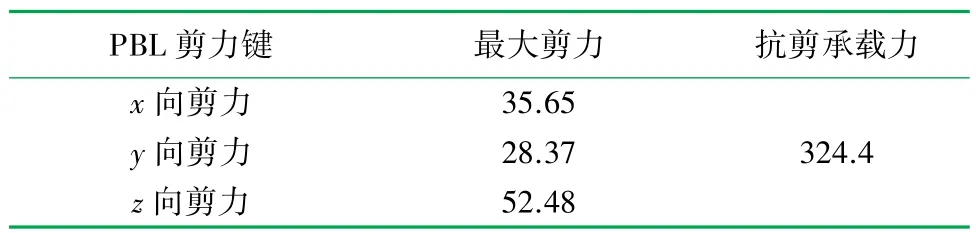
表2 剪力键受力表/kN

3.3.2 剪力钉计算结果

剪力钉受力计算结果见表 3，最大剪力为69.66 kN，其值＜106.4 kN，表明剪力钉最大剪力小于其抗剪承载能力，满足规范要求。

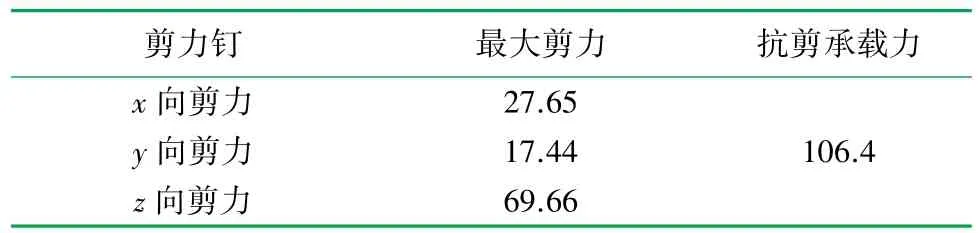
表3 剪力钉受力表/kN

3.4 承压板厚度对结合段的受力性能影响分析

所建模型中，钢—混结合段承压板厚度为40 mm。为研究承压板厚度改变对钢—混结合段受力性能的影响，在边界条件、外部荷载及其余构件参数不变的前提下，分别调整承压板厚度为20、30、40、50、60、70 mm，分析承压板厚度改变对结合段顶板、底板、腹板及承压板的Mises应力影响，计算结果如图5所示。

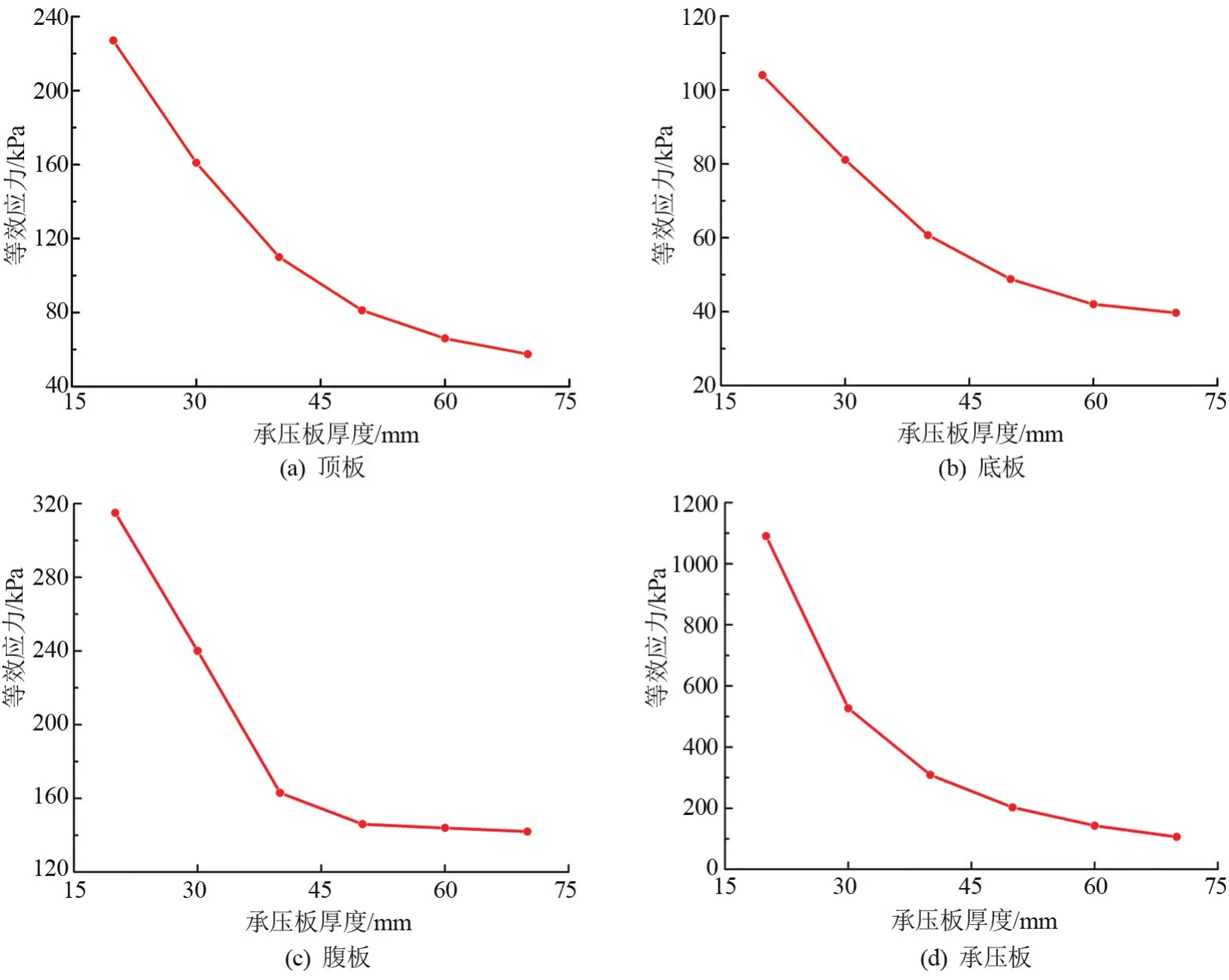
图5 钢—混结合段各构件Mises应力与承压板厚变化曲线图

由图5可以看出，随着承压板厚度的增加，顶板、底板、腹板及承压板的Mises应力均呈减小趋势，表明承压板厚度的增加能有效降低结合段钢构件的Mises应力水平，同时随着承压板厚度的增加，在承压板与加劲肋以及预应力钢筋锚固处存在的较为明显的应力集中现象将会得到改善。由此可以看出，增加承压板的厚度可以有效缓解结合段连接处的局部应力集中现象。

4 结论

通过上述研究可知:

(1)除在承压板预应力束锚固区、混凝土剪力钉锚固区及箱梁顶板与腹板交接处局部较小区域出现应力集中现象外，钢—混结合段的钢箱梁和混凝土箱梁应力满足规范要求。剪力钉最大剪力为69.66 kN，小于其抗剪承载力106.4 kN；PBL剪力键最大剪力为52.48 kN，小于其抗剪承载力324.4 kN，剪力钉及PBL剪力键最大剪力均满足规范要求。

(2)承压板厚度的增加能有效降低结合段钢构件的应力水平，缓解结合段连接处的局部应力集中现象。混合连续梁桥钢—混结合段内力传递较为平顺，应力水平较低，具有良好的安全储备，结构构造合理，对于局部应力集中现象，受力较复杂，应加强构造措施，保证施工质量。