场地及碰撞效应对连续刚构桥剪切易损性影响

赵金钢李晰贾宏宇杨灿

(1.贵州大学 土木工程学院，贵州贵阳550025；2.西南交通大学 土木学院，四川 成都610031；3.湖北省交通规划设计院股份有限公司，湖北武汉430051)

0 引言

地震荷载产生的水平力主要由桥梁墩柱承受，因此墩柱必须具有足够的抗震能力，以保证桥梁结构的安全。通过钢筋混凝土墩柱模型拟静力试验研究表明，在动力荷载作用下，墩柱首先产生弯曲屈服，并由于塑性铰区抗剪能力退化而发生剪切破坏，直至丧失竖向承载力而发生倒塌破坏，墩柱的倒塌破坏通常伴随剪切破坏而产生。

剪切破损属于脆性破坏，是钢筋混凝土墩柱的一种危险的破坏形式。我国2008年发生的汶川大地震中，百花大桥和高树大桥均有墩柱因发生弯剪破坏而导致桥梁损伤破坏[1]；美国北岭地震、日本阪神地震等地震中也均有桥梁墩柱发生剪切破坏的工程实例发生。当前，在进行桥梁墩柱地震抗剪能力设计时，仍采用墩柱的剪切强度大于墩柱可能在地震中承受的最大剪力的能力设计原则[2]。为研究在确定的地震荷载作用下，钢筋混凝土墩柱的抗剪强度，学者们开展了大量的往复荷载作用下钢筋混凝土墩柱模型抗剪强度试验[3-4]，并根据试验结果提出了钢筋混凝土墩柱抗剪强度计算公式。各国抗震设计规范已采用了部分研究结果。但是，由于剪切作用机理极为复杂，当前尚未形成相对统一的考虑墩柱剪切作用的分析理论和方法[5]。此外，由于地震波的随机性，使得桥梁结构的地震响应也具有随机性，通常采用易损性分析方法研究桥梁结构在特定加速度峰值地震波作用下发生损伤的概率。但是，由于桥梁剪切损伤作用机理的复杂性，现有的研究多集中于弯曲破坏的易损性研究，而对于桥梁墩柱剪切易损性的研究开展尚少。其中，张菊辉[6]以规则连续梁桥为研究对象，通过墩柱所需最大剪力与位移延性系数之间的关系，得到墩柱剪切破坏对应的位移延性系数，并对钢筋混凝土墩柱进行剪切易损性分析；董俊[7]以某铁路高墩刚构—连续组合体系桥梁为研究对象，建立了高墩剪切破坏状态方程和损伤判别准则，并开展了空间地震动作用下钢筋混凝土高墩剪切易损性分析。

文章以某钢筋混凝土高墩连续刚构桥工程实例为研究对象，建立OpenSees空间有限元模型，开展钢筋混凝土高墩桥梁地震剪切易损性分析。由于高墩柔性较大，高墩桥梁第一阶甚至前几阶振型均为纵向振动，从而使得梁体发生纵向碰撞的概率倍增；当地震发生时，地震波从震源位置沿基岩传递到桥位处，然后向上穿过土层到达桥梁结构的基础，由于土层对地震波的过滤作用，对地震波强度的影响十分显著[8]。因此，文章应用DEEPSOIL软件考虑实际场地土层对地震波的过滤作用，并在OpenSees模型中采用碰撞单元模拟桥梁碰撞效应，以基岩地震波加速度峰值为强度指标，通过增量动力非线性分析，研究实际场地土层分布和碰撞效应对钢筋混凝土高墩剪切易损性的影响，其成果可用于新建钢筋混凝土高墩桥梁地震抗剪性能分析，并为既有桥梁抗震加固设计提供参考依据。

1 高墩连续刚构桥有限元模型

依托工程实例的钢筋混凝土高墩大跨连续刚构桥的跨径布置为(88+168+88)m，主梁采用顶板宽为12 m、底板宽为8 m的单向单室变截面形式；全桥设有2个不等高度的主墩:次高墩(2#墩)和高墩(3#墩)，其高度分别为75、103 m，且均采用变截面空心矩形薄壁墩。全桥布置及桥位处地质情况如图1所示。

采用有限元软件OpenSees建立钢筋混凝土高墩大跨连续刚构桥的空间有限元模型，如图2所示。由于主梁在地震荷载作用下通常处于弹性状态，因此文章应用基于位移的梁柱单元和弹性截面联合模拟主梁结构；桥墩底部会由于地震荷载的作用产生非常大的内力，并进入弹塑性状态，因此采用纤维截面来模拟桥墩的非线性行为，并且通过对同一单元两端节点赋予不同截面属性的方法来模拟高墩的截面尺寸变化；墩底部采用固结约束模拟；采用连接单元模拟梁端盆式橡胶支座，并按照JTG/TB 02-01—2008《公路桥梁抗震设计细则》[9]确定模拟支座滑动向非线性行为的双线性滞回材料的相关参数取值。由于箍筋对高墩混凝土的约束作用，将高墩截面混凝土分为约束混凝土和非约束混凝土2部分，如图2所示。因此，文章采用Concrete02模型模拟非约束混凝土和约束混凝土的本构关系，并按照文献[10]确定Concrete02模型的相关参数取值；钢筋材料采用Steel02模型模拟。

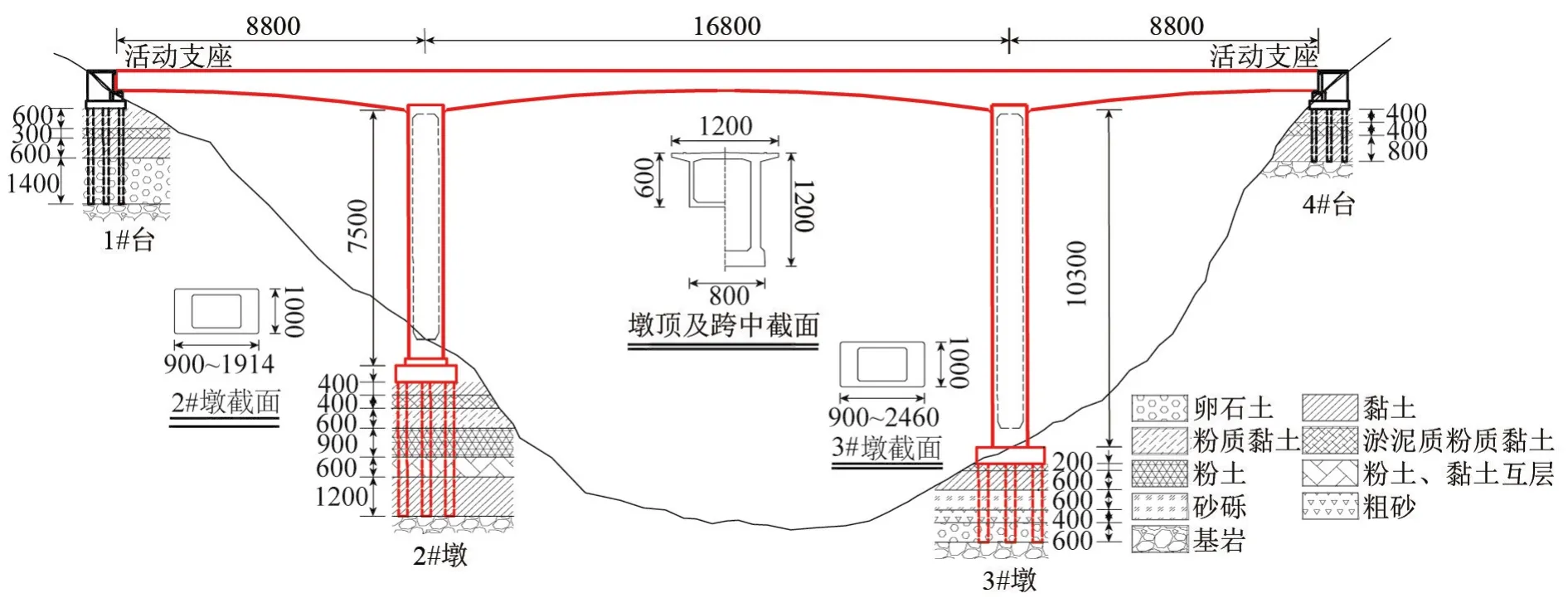
图1 钢筋混凝土高墩大跨连续刚构桥布置图/cm

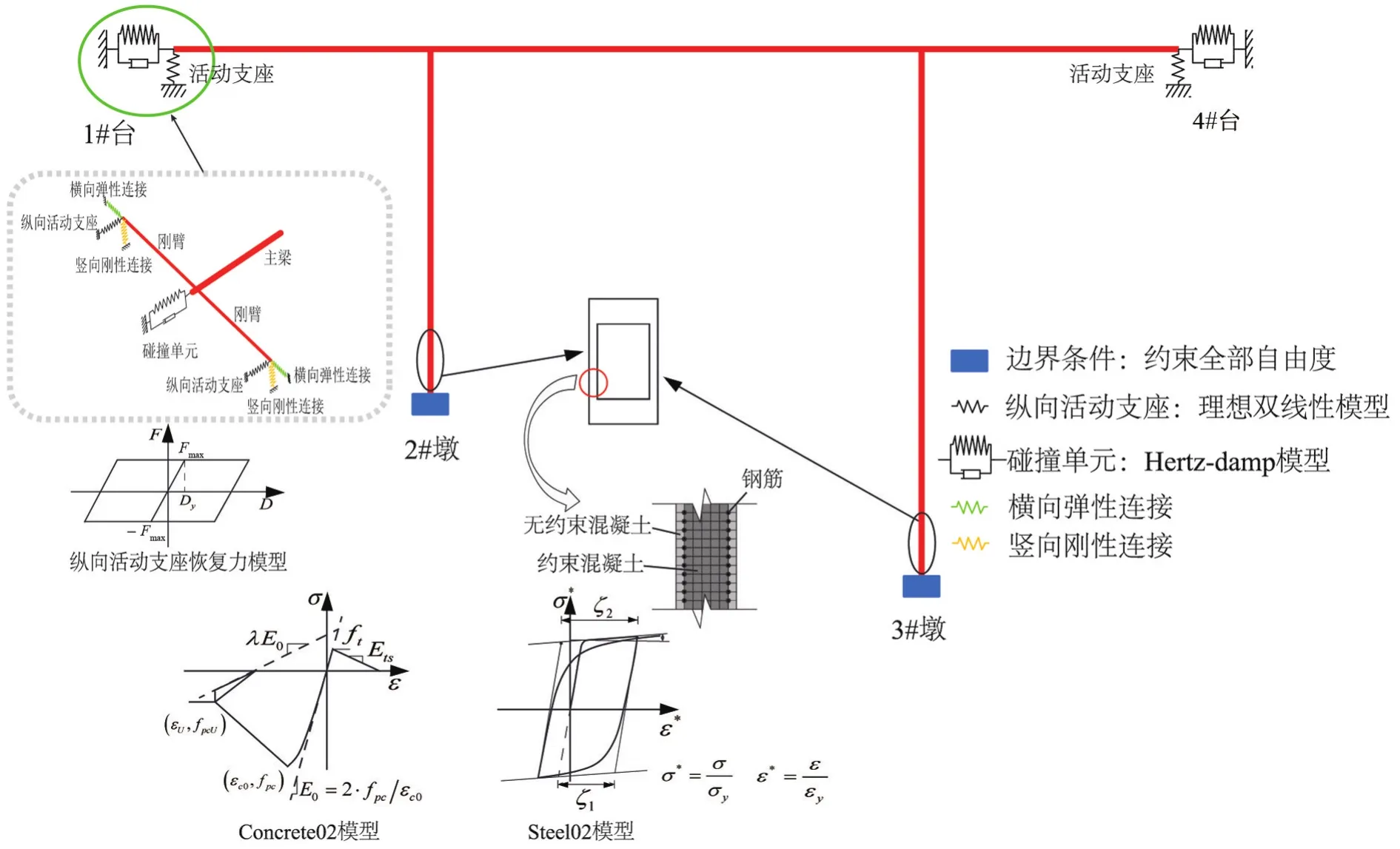
图2 有限元模型图

文章采用Hertz-damp模型模拟主梁与桥台之间的碰撞效应，以准确分析地震荷载作用下主梁与桥台之间的碰撞效应。Hertz-damp模型采用非线性弹簧和非线性黏滞阻尼器的组合模拟碰撞效应，如图3所示。在实际应用时，通常将此模型简化为双线性刚度接触模型，如图4所示。碰撞力F由式(1)表示为

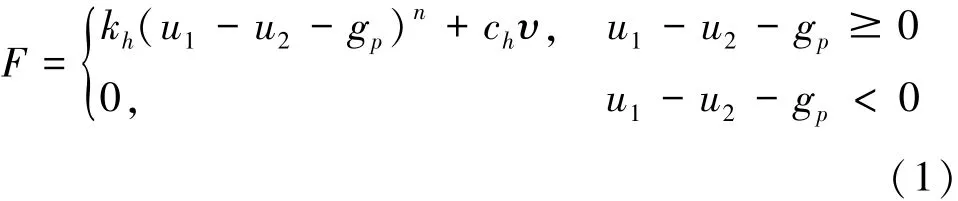
式中:ch为阻尼系数；kh为碰撞刚度，一般典型取值为碰撞结构物的轴向刚度，kN/mm3/2；u1、u2为碰撞体位移，mm；gp为相邻碰撞体之间的间距，mm；n为Hertz系数；v为相对速度，m/s。

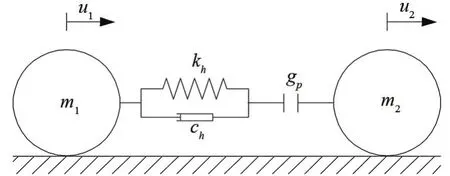
图3 结构碰撞分析模型示意图

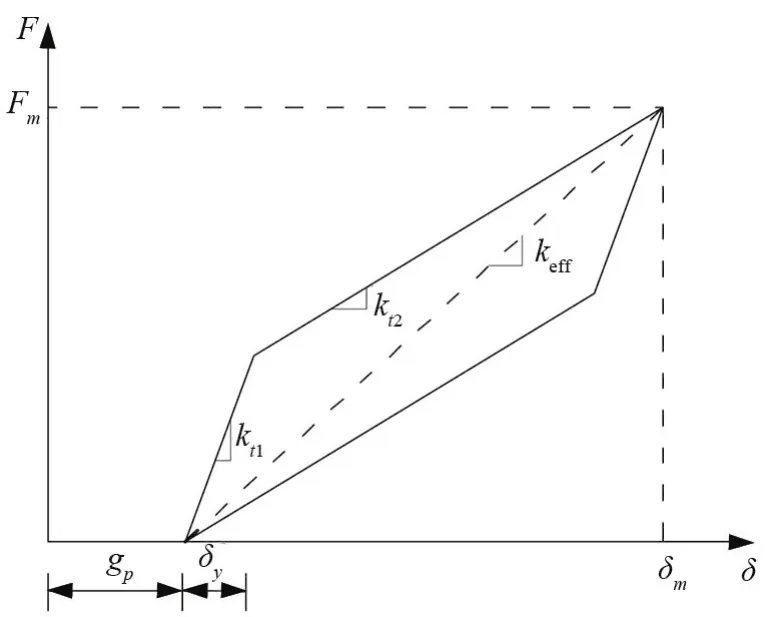
图4 Hertz-damp模型示意图

在图4所示的双折线模型中，假设Hertz-damp理论模型和简化模型的最大碰撞力Fm是相等的，则等效刚度keff由式(2)表示为

式中:δm为碰撞时2接触面最大入侵位移，mm。

同时，采用初始刚度kt1和应变强化刚度kt2表示等效刚度keff的另一种形式，由式(3)表示为

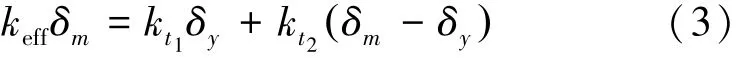
式中:δy为屈服位移，mm。

碰撞力和位移所围成的区域面积Am可由式(4)表示为

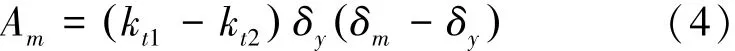
碰撞过程中所耗散的能量ΔE由式(5)表示为

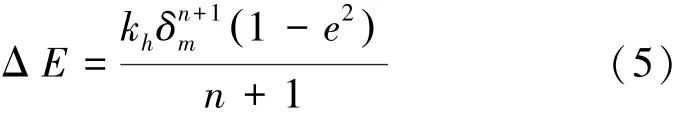
式中:e为恢复系数。

屈服位移δy与最大侵入位移δm之间的关系，可由式(6)表示为

式中:a为屈服系数。

在碰撞过程中，碰撞模型耗散的能量ΔE与碰撞力—位移所围双折线区域面积Am相等，即Am=ΔE，并结合式(1)～(6)，可得初始刚度kt1和应变强化刚度kt2由式(7)表示为

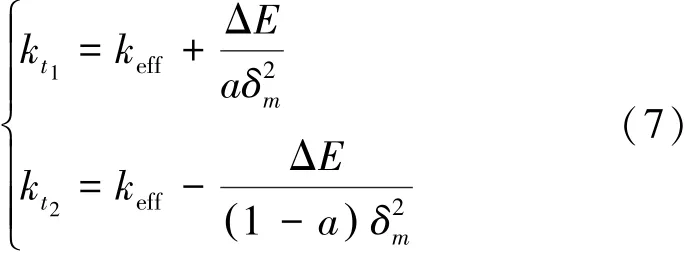
由式(7)可知，只要确定kh、e、δm和a，就可以计算出Hertz-damp模型的各参数值，所取特征参数见表1。

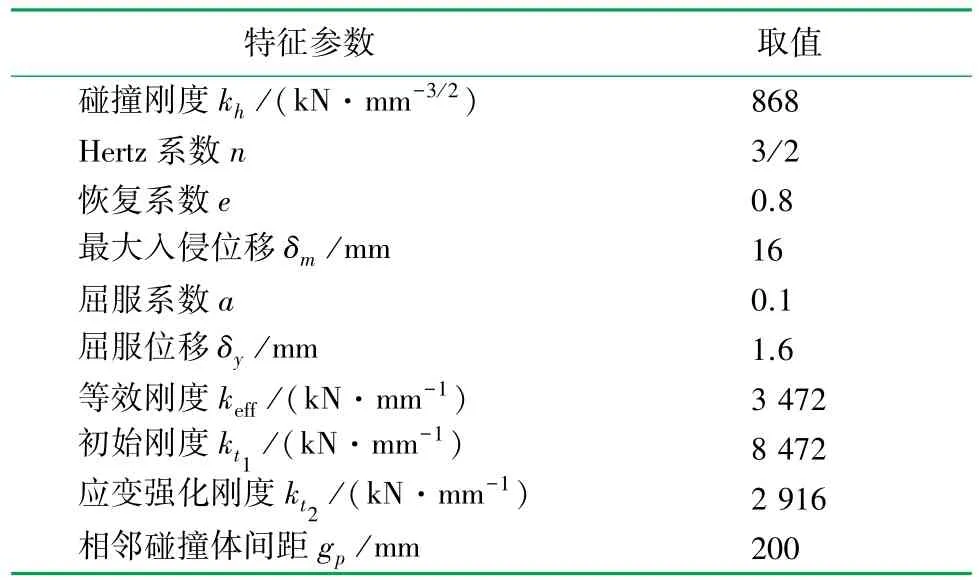
表1 Hertz-damp简化模型特征参数表

2 土层过滤效应分析

2.1 基岩地震波选取

文章从太平洋地震研究中心(PEER)提供的强震地震波数据库[11]中选取20条剪切波速Vs30＞750 m/s的基岩地震波，并且所选取基岩地震波的震级为6.20～7.62度；最大地震动加速度峰值为0.862g，而最小地震动加速度峰值为0.018g，涵盖了大、中、小三级地震动。图5中给出了阻尼比为5%、峰值加速度为1.0g时基岩地震波的绝对加速度反应谱，其离散性反映了选取基岩地震波的不确定性。

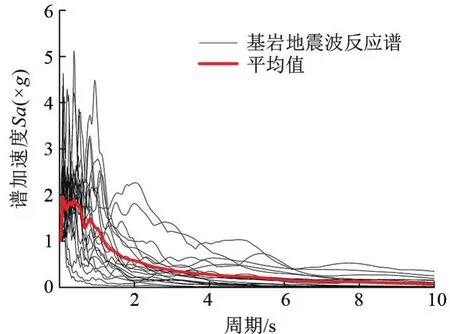
图5 基岩地震波反应谱曲线图

2.2 土层过滤效应分析

在地震过程中，从基岩传递到土层的剪切地震波使土体产生交变应力，土体表现出非线性特性，导致地震波的峰值加速度和频谱特性发生变化。因此，能否准确地分析土层对基岩地震波的过滤作用是结构地震动输入是否准确的基础。采用能够考虑土层非线性效应的DEEPSOIL软件计算分析土层对地震波的过滤作用，DEEPSOIL软件是由美国伊利诺伊大学香槟分校的Hashash等[12]开发的一款用于一维场地地震响应分析的软件，可以通过对土层非线性参数的拟合得到时域非线性分析所需的参数，降低了参数确定的难度，并且提供了交互式输入方式，简便易学，在土层地震响应分析中得到大量应用。

Matasovic等[13]提出的修正双曲线本构模型可以考虑土层深度对土层非线性参数的影响，如图6所示，其初始骨架曲线由式(8)表示为

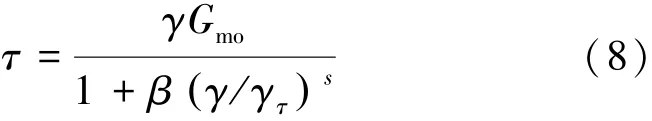
式中:τ为剪应力，MPa；Gmo为初始剪切模量，MPa；γ为已知剪应变；γτ为参考剪应变；β、s为拟合参数。

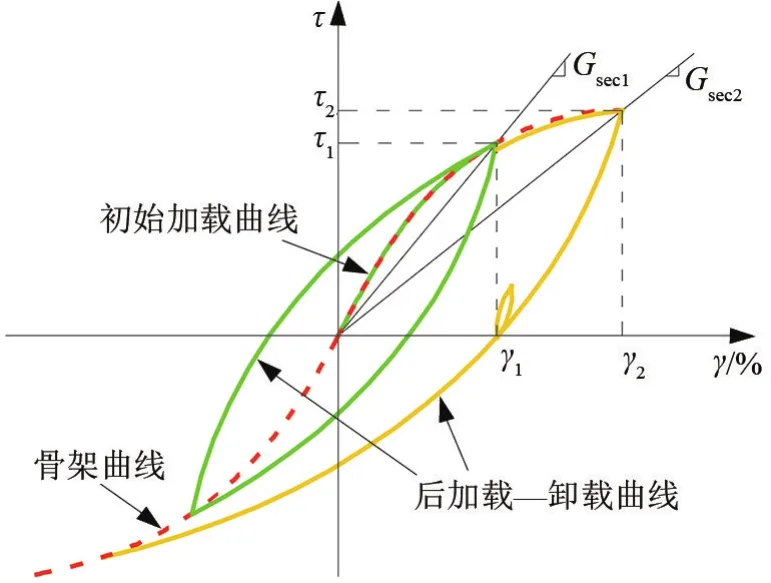
图6 双曲线本构模型图

参考剪应变γτ与土层特性有关，可由式(9)表示为

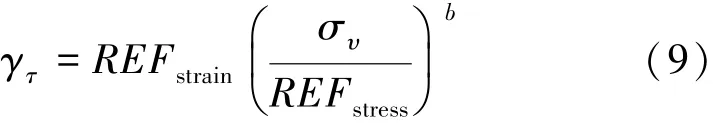
式中:συ为竖向有效应力，MPa；REFstrain为参考有效应变；REFstress为参考压应力，通常取0.18 MPa；b为拟合参数。

小应变阻尼λ由式(10)表示为

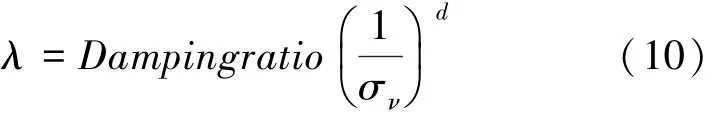
式中:Dampingratio和d为小应变阻尼比拟合参数。

进行时域非线性分析时，除土层的厚度、剪切波速、密度等参数外，还有小应变阻尼比Dampingratio、REFstress、REFstrain和β、s、b、d等需要确定或拟合。DEEPSOIL软件可以通过对剪切模量变化曲线(G/Gmax-γ曲线)和阻尼比变化曲线(λ-γ曲线)的拟合得到上述参数。图1中给出了1#桥台、2#桥墩、3#桥墩和4#桥台处场地土层构成和各类土的土层厚度，并且通过钻孔资料获得了各类土样的资料(见表2)，同时表3中给出了桥位处各类土样的G/Gmax-γ曲线和λ-γ曲线。其中，rd为土体剪应变幅值；G/Gmax为动剪切模量比；λ为阻尼比；粉土、黏土互层非线性参数与黏土相同。

将图1和表2、3中的桥位处场地土层分布和各类土的特征值输入DEEPSOIL软件，建立土层过滤效应的计算模型，并拟合得到各非线性参数。同时将所选取的20条基岩地震波加速度峰值按比例调整为 0.05g、0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g、0.8g、0.9g和1.0g后，分别输入DEEPSOIL软件，计算分析土层对基岩地震波的过滤作用，得到1#桥台、2#桥墩、3#桥墩和4#桥台处的地表地震波。因篇幅限制，此处仅列出地表地震波与基岩地震波的平均反应谱对比图，如图7所示。

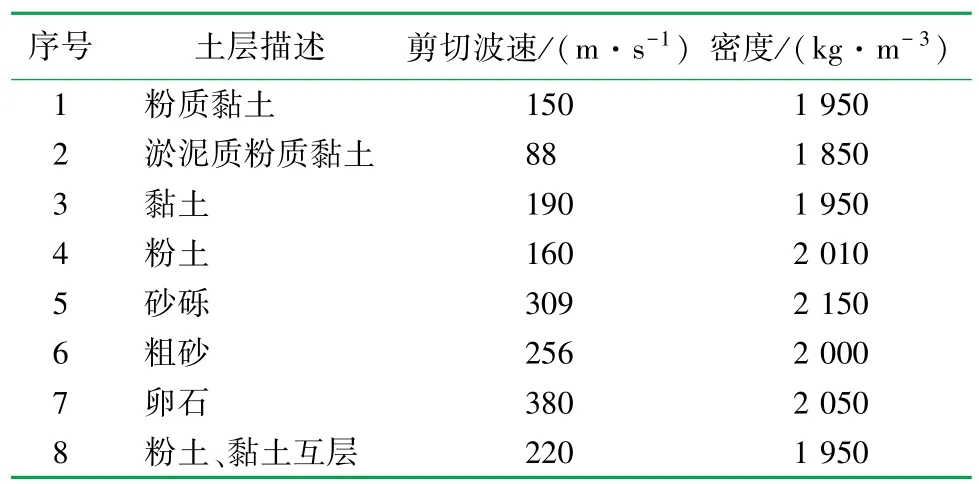
表2 土样试验参数表

表3 土样非线性参数

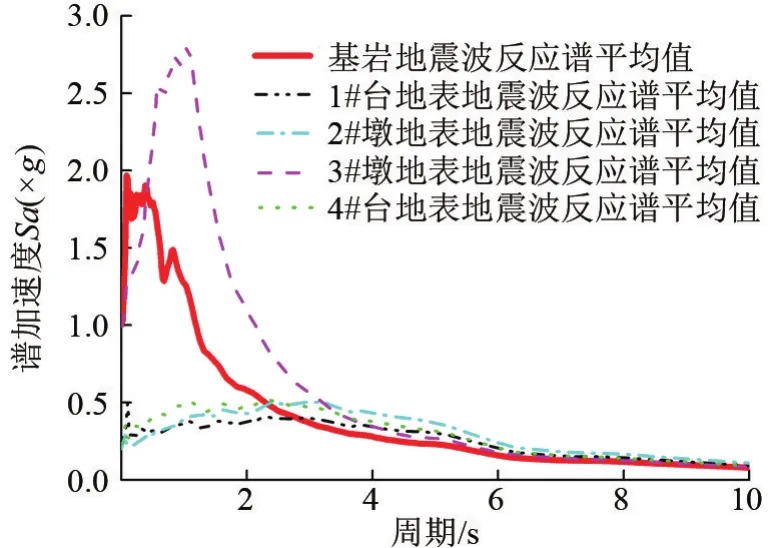
图7 地表地震波与基岩地震波的平均反应谱对比图

由图7可知，3#桥墩处的土层对基岩地震波的平均反应谱峰值放大了1.5倍，而1#桥台、2#桥墩和4#桥台则缩小为原来的1/4倍，因为3#桥墩处土层以卵石、砂砾和粗砂分布为主要成分，根据其剪切波速(见表2)可以判断该处土层较硬，其振动频率跟基岩地震波频率相近，产生共振，故对基岩地震波有放大作用，反之，1#桥台、2#桥墩和4#桥台处对基岩地震波又有缩小作用。

3 场地及碰撞效应对高墩连续刚构桥剪切易损性影响分析

3.1 抗剪承载力计算方法

当前常用的桥梁墩柱抗剪承载力公式主要有Priestly等[14]提出的计算公式和美国Caltrans抗震设计准则[15]推荐的计算公式，2个均可以考虑弯曲延性对桥墩剪切强度的折减作用，此外Priestly公式还可以单独考虑轴压力桥墩抗剪强度的影响，以分析轴压力的对桥墩抗剪强度的提高作用。但是，对于空心截面桥墩，轴压力对抗剪承载力提高的影响要远小于实心桥墩，可以忽略轴力对空心桥墩抗剪承载力的贡献[16]。由于实例桥梁采用的是钢筋混凝土空心薄壁桥墩，并且JTG/TB 02-01—2008[9]给出的墩柱塑性铰区斜截面抗剪强度计算公式也是对Caltrans抗震设计准则推荐的计算公式进行简化处理得到的。因此，采用Caltrans抗震设计准则推荐的桥梁墩柱抗剪承载力计算公式高墩抗剪性能分析，可由式(11)表示为

式中:Vn为桥墩名义抗剪能力，kN；Vc为混凝土提供的抗剪能力，kN；Vs为箍筋提供的抗剪能力，kN。

混凝土提供的抗剪强度Vc由式(12)表示为

式中:Ae为混凝土有效剪切面积，Ae=0.8Ag，m2；Ag为桥墩的毛面积，m2；νc为名义剪应力，MPa，其在塑性铰区域内、外分别满足式(12)和(13)为

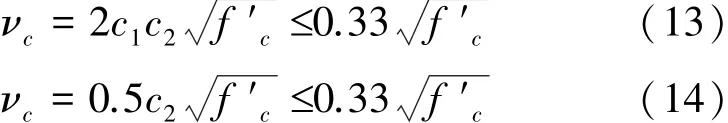
式中:f′c为混凝土圆柱体抗压强度，MPa；c1、c2分别为与桥墩位移延性系数和轴压比有关的系数，分别由式(15)和(16)表示为

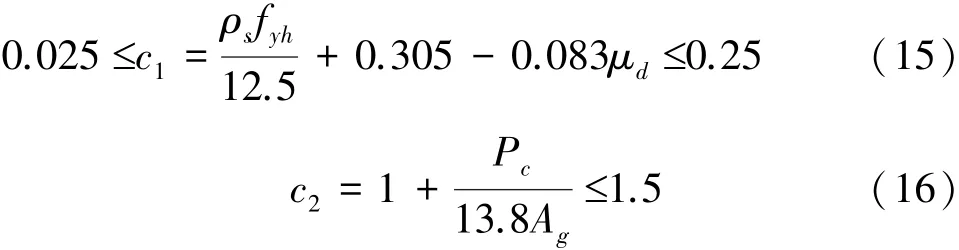
式中:ρs为箍筋配箍率；fyh为箍筋屈服强度，MPa；Pc为桥墩受到的轴压力，kN；μd为桥墩位移延性系数，可根据桥墩的屈服位移和极限位移计算确定。

由于实例桥梁采用矩形截面桥墩，因此箍筋提供的抗剪能力Vs由式(17)表示为

式中:Av为同一截面上箍筋的总面积，m2；s为箍筋间距，m；fyh为箍筋的抗拉设计强度，MPa；d为沿计算方向桥墩的宽度，m。

3.2 剪切损伤指标

剪切荷载作用下，钢筋混凝土墩柱在尚未形成完整斜裂缝之前，剪切荷载主要由混凝土承担，并且随着斜裂缝的开展，混凝土承担的剪切荷载迅速减小，而与斜裂缝相交的箍筋分担的剪切荷载迅速增大，随斜裂缝的进一步增大，其数量增加、宽度逐渐增大，因此，可将斜裂缝的开展情况及相应荷载作为钢筋混凝土墩柱剪切损伤状态的划分标准。根据文献[7]的研究成果，将剪切荷载作用下钢筋混凝土墩柱的剪切损伤状态划分为:无损伤、轻微损伤、中等损伤、严重损伤和完全损伤等5个阶段，剪切损伤状态判断准则见表4。其中，Vc2为钢筋混凝土墩柱第一条完整斜裂缝出现时对应的抗剪强度值，取为3.1节中混凝土抗剪强度Vc；Vc4为桥墩名义抗剪强度，根据3.1节计算确定；Vc1可取为中等损伤临界值Vc2的 6/7 倍，即Vc1为 0.862Vc2；Vc3为(Vc4+Vnd)/2，其中Vnd为钢筋混凝土墩柱延性抗剪强度，可根据文献[3]和3.1确定。

表4 桥墩剪切损伤阶段划分及损伤准则表

3.3 剪切易损性分析

易损性曲线表示在不同强度的地震波激励荷载作用下，结构响应超过损伤阶段量化指标界限值的条件概率。根据文献[7]的研究成果，假定在相同峰值加速度的基岩地震波作用下，高墩截面剪力最大值服从对数正态分布，则在某一强度基岩地震波激励荷载作用下，高墩的剪切损伤概率由式(18)表示为

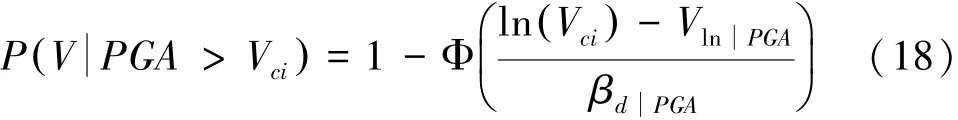
按照以下4个工况对比研究实际场地和碰撞效应对钢筋混凝土高墩大跨连续刚构桥剪切易损性的影响:工况一 不考虑碰撞和场地效应；工况二 考虑场地效应，但是不考虑碰撞效应；工况三 考虑碰撞效应，但是不考虑场地效应；工况四 同时考虑碰撞和场地效应。

文献[17]中研究表明，相比于地震动不确定性，结构不确定性对地震概率需求模型影响较小。因此，采用结构确定性参数按照上述的方法建立实例桥梁有限元模型，其中工况一和工况二的有限元模型中不建立碰撞单元。为考虑场地效应，将选取的基岩地震波调整峰值加速度后，采用DEEPSOIL软件生成1#桥台、2#桥墩、3#桥墩和4#桥台处的地表地震波，并将其沿纵桥向输入工况二和工况四对应的模型中，进行多点激励作用下的增量动力非线性分析(IDA分析)，对不考虑场地效应的工况一和工况三，直接采用基岩地震波进行IDA分析，并记录各工况下2#和3#墩的剪力响应；最后按照式(18)对各工况的2#墩和3#墩底截面进行剪切易损性分析，并绘制易损性曲线，如图8、9所示。

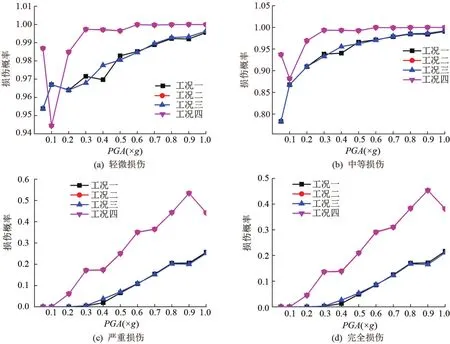
图8 2#墩剪切易损性对比曲线图

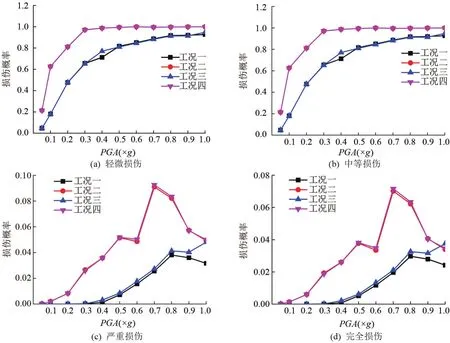
图9 3#墩剪切易损性对比曲线图

由图8、9可知，碰撞效应对高墩剪切损伤影响较小，而场地效应对高墩剪切损伤影响较大，并且场地效应提高了2#和3#墩各损伤阶段的剪切损伤概率，剪切损伤概率分别提高了28.5%和44.6%；2#墩发生轻微损伤和中等损伤的概率均较大，并且在基岩地震波峰值加速度达到0.3g时，发生轻微损伤和中等损伤的概率接近于100%；2#墩发生严重损伤和完全损伤的概率随峰值加速度的增加而逐渐增大，并且在峰值加速度达到0.9g时，损伤概率最大，分别为53.4%和45.3%；基岩地震波峰值加速度较小时，3#墩发生轻微损伤和中等损伤的概率较小，并随峰值加速度增加而迅速增大，峰值加速度达到0.3g时，发生轻微损伤和中等损伤的概率接近于100%；3#墩发生严重损伤和完全损伤的概率较小，均＜10%。

4 结论

文章以某钢筋混凝土高墩大跨连续刚构桥为研究对象，采用OpenSees建立有限元模型，同时考虑实际场地土层分布对基岩地震波的过滤作用和主梁与桥台之间的碰撞效应，通过IDA分析获得2#墩和3#墩的剪力响应，并采用概率分析方法对钢筋混凝土高墩墩底截面进行了剪切易损性分析，所得结论如下:

(1)高墩(3#墩)处土层较硬对地震波具有放大作用，使得3#墩处地表地震波的平均反应谱峰值为基岩地震波反应谱峰值的1.5倍，而桥台和次高墩(2#墩)处地表地震波反应谱峰值缩小为基岩地震波的1/4倍。

(2)碰撞效应对2#、3#墩的剪切损伤影响均较小，而场地效应提高了2#、3#墩各损伤阶段的剪切损伤概率。因此，高墩剪切损伤概率受碰撞效应影响较小而受场地效应的影响较大，并且场地效应对3#墩剪切易损性的影响大于2#墩。

(3)2#、3#墩发生轻微损伤和中等损伤的概率均较大，当基岩地震波峰值加速度达到0.3g时，发生轻微损伤和中等损伤的概率均接近于100%，并且2#墩有较大的概率发生严重损伤和完全损伤，而3#墩发生严重损伤和完全损伤的概率较小，均＜10%。高墩大跨连续刚构桥进行抗震设计时，应考虑实际场地效应对高墩剪切损伤的影响。