基于Kondo粒子散射的电子自旋纠缠

张浩，赵俊卿

(山东建筑大学理学院，山东济南250101)

0 引言

信息科学在推动社会文明进步和提高人类生活质量方面发挥了巨大的作用。随着人类对信息需求的日益增加，量子信息学成为人们关注的重点[1-6]。量子特性在信息领域中有着独特的功能，即在提高运算速度、确保信息安全和增大信息容量等方面，具有突破经典信息系统的能力。量子信息学以量子力学基本原理为基础，通过研究量子系统的各种特性，如量子并行、量子纠缠和量子不可克隆等，得到各种因素对量子信息传输的影响关系，选取最佳条件进行量子计算和量子信息传输。而量子纠缠作为量子计算和量子信息传输的载体，已广泛应用于量子计算、量子隐形传态[7]、量子密码[8]等领域，因此研究量子纠缠具有重要的意义。

由于量子纠缠的重要性，对量子信息学的研究可以看做是对量子纠缠生成、演化的研究。1996年，第一个纠缠浓缩方案提出[9]，其是利用Schmidt投影方法实现的。之后，学者们提出了很多的纠缠态浓缩方法。尤文龙等[10]研究了由杂质自旋散射引起的纠缠；王琼[11]研究了三量子点与四量子点系统中量子纠缠的产生；任杰等[12]研究了带有次近邻相互作用和三体相互作用的自旋S=1一维自旋链中的量子纠缠；刘贵艳等[13]研究具有次近邻相互作用五量子比特XXZ海森伯自旋链在磁场作用下的热纠缠。非最大纠缠态在量子信息处理中会降低方案的精确度和安全性，量子纠缠浓缩可以将非最大纠缠态转变为最大纠缠态，提高信息处理的品质和安全性。赵瑞通等[14]通过电子自旋辅助，实现了光子偏振态的量子纠缠浓缩。

Kondo粒子是指粒子具有自旋不固定的孤立磁矩，并与自由电子发生自旋相互作用，为研究粒子间的量子纠缠提供了一个很好的理论模型。文章基于Kondo粒子的散射理论，研究自旋不固定的Kondo粒子散射对电子自旋状态的影响，以期为调控电子自旋的纠缠程度以及量子信息传递提供理论基础。

1 Kondo粒子散射理论模型

基于Kondo粒子散射模型，研究Kondo粒子对自由电子自旋的影响。考虑Kondo粒子对自由电子的散射过程，将系统的哈密顿量H[4]由式(1)表示为

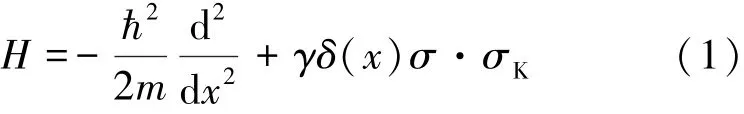
式中:h-为约化普朗克常数；m为自由电子质量；σ为电子自旋；δ为势垒函数；γ为δ势的大小；σK为散射粒子自旋算符矢量。

按照分波法[15]的3个步骤，在角动量耦合表象，用Bell基将电子—粒子相互作用的本征矢量由式(2)表示为

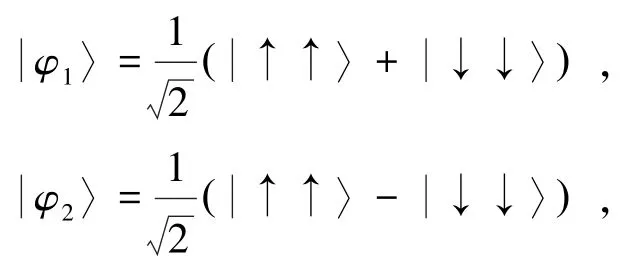
该组本征态φn〉(n=1，2，3，4) 也是σ·σK的本征态，对应的本征值为λn，可由式(3)表示为

式中:Dn为本征态的比例系数。

将每一个本征态对应的本征值作为有效势求解散射过程。对于本征态，将入射电子态表示为代入薛定谔方程，由式(5)表示为

可得式(6)表示为

式中:E为本征能量。

(1)当x=0时，由式(6)对x积分，可得式(7)为

此为δ势场中ψ′(0)的跃变条件。

(2)当x≠0时，式(6)变成式(8)为

其解由式(9)表示为

式中:A、B、C为散射系数；j为复数；k为波矢。

由x=0处波函数的连续性条件及其导数的跃变条件式(7)，求得反射系数和透射系数Rn和Sn由式(10)表示为

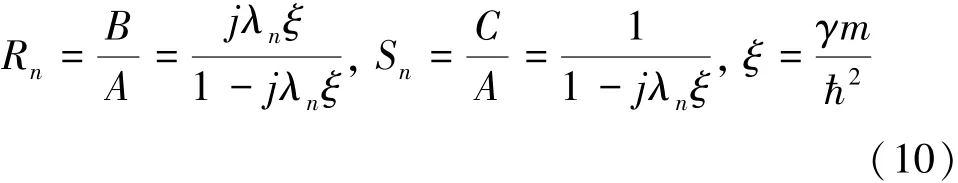
式中:变量ξ的大小只与势垒γ的大小有关。

对不同本征态对应的散射态进行相干叠加。若入射波为所有本征态的线性组合e-jkxχ〉，则散射电子态由式(11)表示为

2 基于Kondo粒子散射的电子自旋纠缠结果与分析

在x＞0的散射电子态即透射态中，由于透射系数Sn不同，不同态的振幅衰减程度不同。所以，Kondo散射过程对入射态电子来说相当于一个自旋过滤器，改变了透射态中的不同自旋成分的比例，可以起到纠缠浓缩的作用。

不同自旋态电子发生散射后，系统透射态的自旋演化见表1。

表1 电子-散射粒子系统透射态的自旋演化表

当入射电子自旋与散射粒子初态自旋方向相同时，两者的自旋状态都不变，不发生自旋纠缠；而当入射电子自旋与粒子初态自旋方向相反时，电子和粒子的自旋状态都有可能变化，并且无法写成直积态，两者发生了自旋纠缠。如散射粒子的初态自旋向上，自由电子处在自旋叠加态即入射态为直积态，则散射态为，已经不是类似初始态的直积态，而变为纠缠态。

考虑到无相互作用的2个自由电子X和Y经同一Kondo粒子依次散射，将基矢按照 YXK〉=的形式表示，有 8种情况，由式(12)表示为

基于表1所示的单电子散射自旋演化结果，考虑电子X和Y先后经同一Kondo粒子依次散射，对各入射态χi〉，得到透射态的自旋演化结果见表2。

表2 双电子透射态的自旋演化表

表3 对散射粒子进行测量后的双电子纠缠状态表

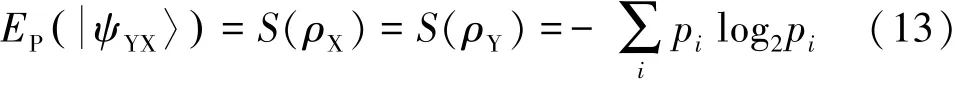
式中:ρX、ρY分别为的密度矩阵对子系统X和Y求迹得到的约化密度矩阵；S为冯诺依曼熵；pi为施密特系数。

利用Mathematica软件编程计算的纠缠度随ξ的变化如图1所示。可以看出，随ξ的变化均呈现一最大值相应的ξ值用ξi表示。当随ξ快速增大，增速更快，即可见，ξ对纠缠度的控制起到关键作用，ξ主要取决于Kondo粒子δ势γ的大小，所以通过调整γ可以对纠缠度进行控制。

图1 X、Y电子的纠缠度EP随ξ的变化图

3 结论

基于Kondo粒子对自由电子的散射理论，研究了自旋可变的Kondo粒子散射对电子自旋状态的影响。主要结论如下:

(1)当自由电子经过Kondo粒子时，电子和Kondo粒子的自旋方向都可能发生变化。Kondo粒子散射改变了入射电子态中不同成分自旋的比例，相当于一个自旋过滤器，可以起到纠缠浓缩的作用。

(2)对先后通过Kondo粒子的2个自由电子自旋态的研究表明，Kondo粒子散射可以使两无相互作用的电子间形成纠缠，纠缠程度取决于初始状态和散射势高度，通过适当调整势垒高度，可以对电子纠缠程度进行有效的控制。