基于场协同理论的供暖房间甲醛扩散模拟研究

张浩王倩丛俊滋项东

(1.山东建筑大学热能工程学院，山东济南250101；2.山东省绿色建筑协同创新中心，山东济南250101；3.山东建筑大学科技处，山东济南250101；4.山东建筑大学材料科学与工程学院，山东济南250101)

0 引言

随着社会的进步和经济、科技的发展，人们的生活水平不断提高，不仅对室内热舒适性及空气品质的要求越来越高，而且对室内装修的质量要求也越来越严[1]。木质地板具有轻质、美观并且可以调节室内温湿度的特点，但木质板材会释放大量的有害物质，污染室内空气。甲醛因其自身的易脱附、强扩散特性而成为室内危害最大的污染物之一。有关调查结果表明，许多民用和公共建筑，室内的空气污染程度是室外空气污染的2～5倍，有的甚至超过100倍[2]。通风可以将室内空气中的甲醛快速排除，进而促进了装修材料中甲醛的释放，是非常有效地去除室内甲醛的方法[3-4]。其中，自然通风是降低室内甲醛浓度最简单有效的方法，但引入新风却增加了空调系统和供暖系统的能耗[5-6]。所以，主要应考虑如何在满足室内热舒适的情况下，采用自然通风，选择合适的污染源摆放位置，使速度场与浓度梯度场的协同效果更佳，进而快速地降低甲醛等有害物质。

净化室内空气污染物的实质是对流传质过程，增强对流传质对室内空气的净化有一定的促进作用。Guo等[7]提出对流传热场协同原理，认为速度场与温度梯度场的配合能强化换热系统。传热是由温度梯度引起的热扩散，而传质是由浓度梯度引起的质扩散，所以基于传热与传质的类比关系，将对流传热场协同原理应用于净化通风系统的传质领域对净化排污有一定的指导意义[8]。Chen等[9-10]将传热场协同原理扩展到传质领域，类比于传质势容耗散函数定义了对流传质过程的势容耗散函数，并利用变分原理求解势容函数极值，获得场协同方程求解室内污染物浓度最低时的速度场，确定最佳通风方式。Wang等[11]采用Fluent模拟了空气净化器及通风策略下，室内挥发性有机物VOCs(Volatile Organic Compounds)的浓度分布情况，发现较好的通风条件更有利于室内的VOCs浓度达到稳定值，且空气净化器能更好地净化室内VOCs。还有学者研究了采用通风系统的办公室内的空气质量及热舒适性，并应用计算流体动力学 CFD(Computational Fluid Dynamics)模型校准了室内的气流流动情况，表明CFD模型可以较精确地模拟室内空气质量及热舒适性[12-14]。文章主要采用CFD方法模拟冬季某地板供暖卧室内，污染源位于不同位置时甲醛的扩散分布情况，并应用场协同理论进一步分析了室内甲醛稀释的对流传质过程，以期为优化通风净化效果提供理论依据。

1 数学模型

1.1 场协同理论

对流换热过程中流体的换热能力的强弱与速度场、温度场的分布特性有关。Guo等[15-16]针对增强换热问题提出了对流换热强化的场协同理论，认为速度场与温度场的协同性对对流换热的强弱有较大的影响。基于传热与传质的类比关系，应用传质场协同理论分析室内污染物扩散过程。

1.1.1 传热场协同理论

对二维层流边界层对流换热过程比拟为有内热源的导热问题，将能量方程进行无量纲化分析[5]，由式(1)表示为

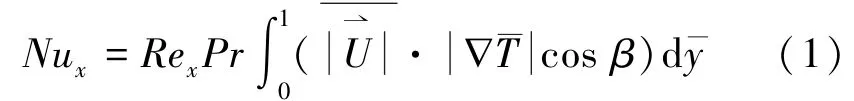
式中:Nux为努谢尔准则数；Rex为雷诺准则数；Pr为普朗特准则数为流体流动的速度矢量的无因次数；为流体温度梯度矢量的无因次数；β为流体速度与温度梯度的夹角。

由(1)式可知，强化换热可以通过增大Re、Pr及无因次积分值。无因次积分值的大小不仅与流体的速度、热流的绝对值有关，还与流速与热流矢量间的协同即夹角有关。两者之间的夹角越小，协同效果越好，换热效果也越好。

1.1.2 传质场协同理论

基于传热、传质过程的类比性，将对流传质过程假定为稳态无组分源项的传质过程[17]，将组分传质方程进行无量纲化分析，由式(2)表示为

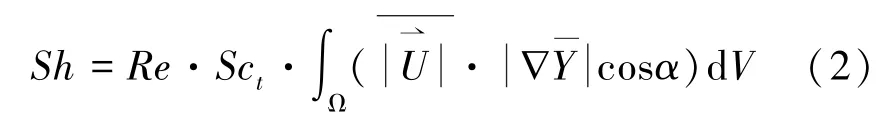
式中:Sh为对流传质的舍伍德准则数；Sct为施密特准则数；为流体质量数梯度矢量的无因次数；α为流体速度与温度梯度的夹角。

Sh是以流体的边界扩散阻力对流传质阻力之比来标志过程相似特征，反映了对流传质的强弱。室内甲醛的稀释扩散过程是典型的对流传质过程，增强对流传质过程即增强室内甲醛的稀释扩散过程。与对流换热强化相类似，增强对流传质过程可以增大Re、Sct及无因次积分值。改变无因次值主要通过改变速度场与浓度场的协同程度，即改变速度场与浓度梯度场的夹角，当夹角越小时，速度场与浓度场的协同效果越好。流体的速度与质量分数的梯度夹角越小，协同效果越好，对流传质效果也越好。文章主要研究自然通风对室内甲醛的稀释扩散过程，而通风对污染物的净化过程是典型的对流传质过程，所以可以应用场协同理论分析室内污染物的排污净化过程。

1.2 控制方程

对房间内的甲醛进行准确的数值模拟，必须建立气体流动规律的控制方程，即质量守恒、动量守恒和能量守恒方程；主要采用标准湍流k-ε模型和气体组分输运模型。

1.2.1 基本控制方程

基本控制方程由式(3)表示为

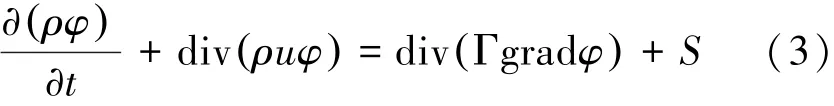
式中:由左至右依次是瞬态项、对流项、扩散项以及源项。其中，φ为通用的变量，可以表示分速度、温度以及常数等；Γ和S分别表示广义扩散系数和广义源项，在质量守恒方程中，φ取1、Γ取0、S取0；在动量守恒方程中，φ取取u、S取；在能量守恒方程中，φ取T、Γ取S取ST。

1.2.2 湍流模型(k-ε方程)

流动能方程(k方程)由式(4)表示为

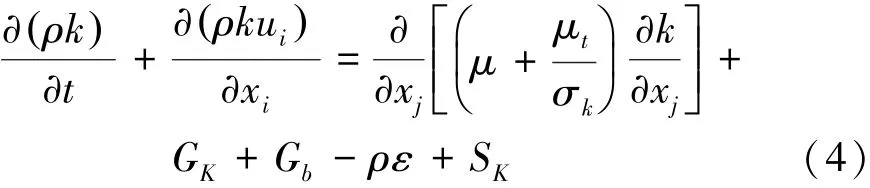
湍流能量耗散率方程(ε方程)由式(5)表示为

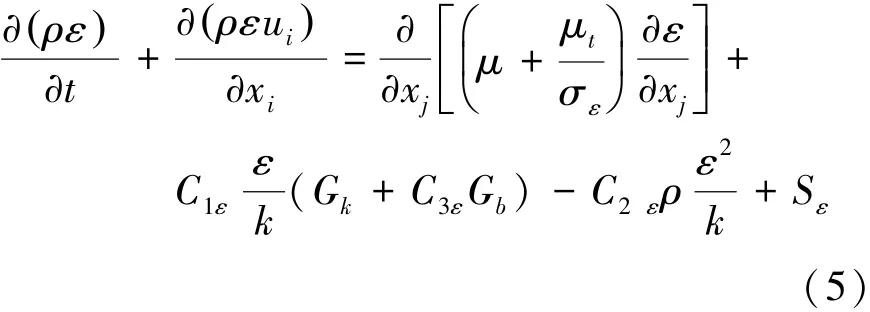
式中:GK为由层流速度梯度产生的湍流流动动能，J；Gb为由浮力产生的湍流动能，J；C1、C2、C3为常量，在空气和水的实验基础上，取C1ε=1.44、C2ε=1.92、C3ε=0.09、σk=1.0 、σε=1.3。

1.2.3 组分输运模型

文章主要研究室内的空气与甲醛混合物，采用组分输运模型模拟室内甲醛分布情况，由式(6)表示为

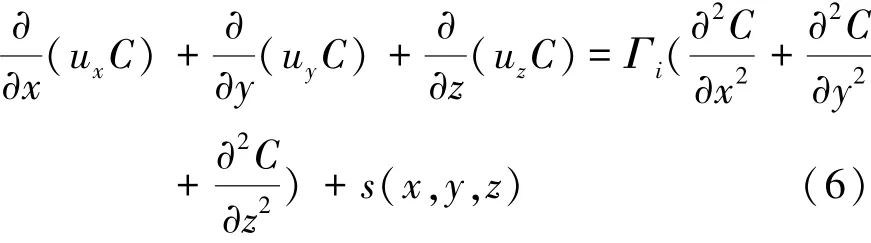
式中:Γi为任一点的扩散系数；s(x，y，z)为任一点的扩散强度；C为室内甲醛浓度，mg/m3。

2 物理模型

2.1 几何模型建立

选取冬季某地板供暖的卧室房间为研究对象，卧室的简化物理模型如图1所示，卧室内设施数量及具体尺寸设置见表1。

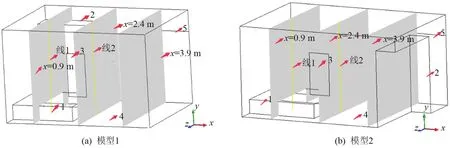
图1 某地板供暖房间的物理模型示意图

表1 卧室模型具体设置表

模型1:污染源衣柜位于通风口对侧；模型2:污染源衣柜位于通风口邻侧。在模型中，选取x分别为0.9、2.4、3.9 m的截面，分别为靠近床人员滞留区、经由窗户及靠近门的3个特殊截面，并对各场进行分析；选取前2个截面上的线1为 (0.9，0，1.9)-(0.9，2.6，1.9)、线 2 为(2.4，0，1.9)-(2.4，2.6，1.9)，对比分析2个模型中甲醛浓度的变化情况。

2.2 网格划分

对物理模型主要采用非结构化网格划分，如图2所示，其划分网格简单且成型比较容易。经网格独立性验证，物理模型中网格数为152 369，其中模型中最大网格尺寸为0.5 m，对衣柜、地板、窗户及门的网格进行加密，网格尺寸为0.2 m，网格质量均＞0.35。

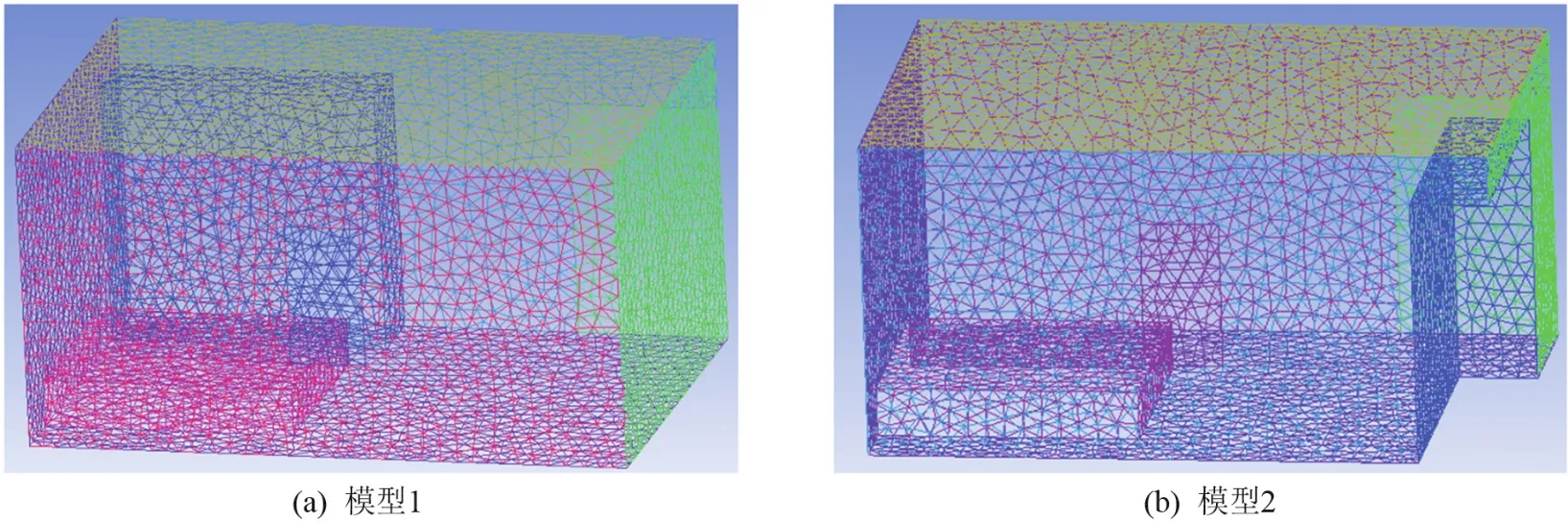
图2 网格划分示意图

2.3 物理模型简化及假设

在模拟分析冬季地板供暖房间的热舒适性及室内空气品质时，对该模型做如下简化:

(1)由于现在房屋的密封性做的都很好，假设该卧室密闭，在门缝及窗缝处无室外空气渗入；

(2)在模拟过程中，将室内空气和甲醛均看作是不可压缩、常物性流体；流体域设定为空气与甲醛的混合物，室内空气流动状态为湍流，且具有高紊流雷诺数；

(3)模拟中将各壁面设定为定壁温稳态传热，忽略室内热源(照明及人体散热)；

(4)模拟中将甲醛的扩散视为单一的物理过程，即扩散过程中不发生化学变化，且不考虑被固体壁面及绿色植物的吸附作用；

(5)对温度场、速度场及甲醛浓度分布情况的分析均在系统达到稳定状态后进行[18]。

2.4 求解边界条件

(1)主要模拟冬季地板供暖房间在自然通风情况下的室内热舒适性及甲醛扩散情况。考虑卧室内的窗户为平开式，且通风时仅开启一半[19]，将窗户设定为速度进口，速度大小取济南冬季室外平均风速为2.7 m/s，新风温度取济南冬季室外平均温度267.8 K，将门设为自由出流边界条件。

(2)东、西、南、北墙壁温度分别选取292、294、295、292 K，地板温度取299 K，屋顶取绝热。

(3)甲醛的散发源选取地板与衣柜，采用质量入口(Mass Flow Inlet)边界条件，其释放强度为7.2×10-11kg/s[20]。

3 模拟结果与分析

3.1 特殊截面处流场的分布

模型中3个截面的流场的分布如图3所示，2种物理模型中的流场的分布差异较大。模型1中，x为2.4 m截面处，空气由窗户进入房间后，以窗户为中心形成速度逐渐衰减的上下2个不同的环流区，且在该截面下部产生一个较小的旋涡，该截面气流平均速度为1.05 m/s。x为3.9 m截面处，空气扰动较大，由于低压与墙壁的约束作用形成2个较小的旋涡，该截面气流平均速度为0.79 m/s。x为0.9 m截面处，空气从靠近柜子房间顶部以0.67 m/s的速度向该截面扩延，在房间右角落部位形成轴心速度较小的涡流。模型2流场分布较模型1明显不同，且在模型2中，各截面的平均流速均较截面1大。x为2.4 m截面处，空气由窗户进入房间后以窗户为轴呈上下2个方向分别向房间扩散，但速度衰减程度较小。x为3.9 m截面处，空气在房间左下角，以速度不断衰减的放射状扩散至房间右上角。在房间上部有2个较小的旋涡产生，该截面气流平均速度为1.31 m/s。x为0.9 m处，靠近床的截面处，由于床及墙壁的约束作用，形成4个较大的旋涡区，在房间上部及床附近区域的旋涡区均以较小的轴心速度以放射状流向房间其他区域，该截面气流平均速度0.77 m/s。整体来看房间内各截面模型2较模型1的气流平均速度较大。

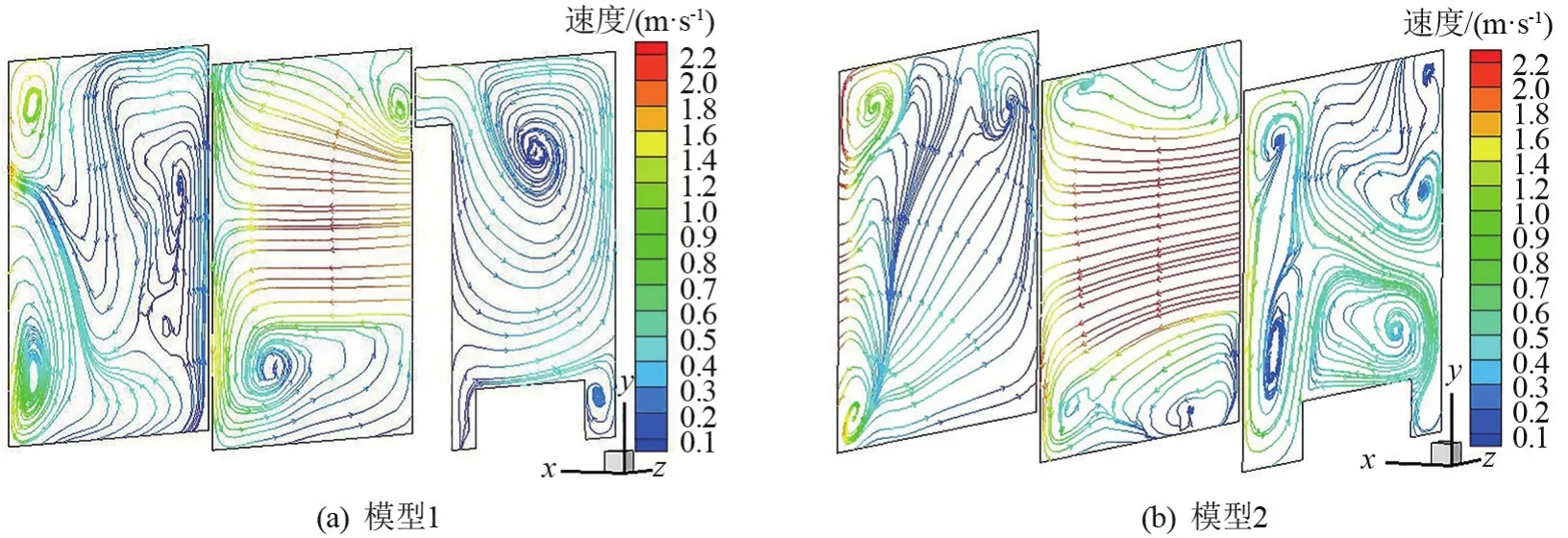
图3 特殊截面流场分布图

3.2 特殊截面处温度场的分布

模型中3个截面温度场的分布如图4所示。地板供暖房间的温度分布在垂直方向上有明显的分层现象，整体上，房间下部温度较上部高。模型1中，x为2.4 m截面处，室外空气由窗户进入室内直接与室内热空气进行热交换，温度较低，在此截面下部由于气流扰动较大，使得冷热空气换热效果较差，下部仍保持较高的温度，此截面平均温度为283.9 K。x为3.9 m截面处，温度有明显的左右两侧的分层现象，靠近门侧由于空气对流作用明显，室内空气与室外冷空气混合较充分，温度较低。而靠近内侧墙壁处，由于气流速度较低且扰动较大，室内外空气混合较不均匀，温度较高，此截面平均温度为285.7 K。x为0.9 m截面处，温度有明显的上下分层现象，床附近温度为296.5 K，且温度波动幅度较小，分布较均匀，平均温度为293.6 K。

模型2中，各截面处温度较截面1低，x为2.4 m截面处，在垂直方向上，窗户高度截面处，冷空气进入房间，在大范围内，温度较低，而房间上部的空气大都是来自室内温度较高的空气，温度较高，此截面的平均温度为275.9 K。x为3.9 m截面处，温度分布与模型1中相似，均呈现由外侧向内侧逐渐升高的分层温度分布，此截面的平均温度较模型1中低为280.2 K。x为0.9 m截面处，温度较模型1有明显的不同的分布，较模型1温度较低，且温度分布也不均匀。由于该截面处速度比模型1速度大，对流换热效果较明显，室内热空气被室外冷空气冷却的程度较大。此截面的平均温度为277.8 K，温度较低，不适合人员在此处长时间停留，因此适合白天人员不在卧室时进行自然通风。

图4 特殊截面温度场分布图

3.3 特殊截面处浓度场的分布

模型中浓度场的分布如图5所示。基于传热、传质的类比关系，浓度场的分布与温度场的分布变化规律相似。可以明显地看出，室内的空气流动对温度场、浓度场的分布影响效果一致，整体上，甲醛浓度分布呈现垂直分层现象，靠近地板处甲醛浓度较高。对比分析模型1、2的x方向不同截面处的浓度分布，x为3.9 m截面处两模型中的浓度分布无明显差异，均以外侧向内侧甲醛浓度逐渐升高的趋势分布。且模型1与模型2中甲醛浓度分别为0.0817、0.0596 mg/m3。x为2.4 m 截面处，模型2较模型1浓度分布明显低，且模型2中下部的浓度梯度较模型1大，变化较明显。模型1、2中甲醛浓度分别为0.0751、0.037 mg/m3。x为0.9 m截面处，两模型中的甲醛质量含量差异较明显，模型2中的甲醛浓度明显低于模型1，尤其在床附近模型2中的甲醛含量较低，模型1与模型2中甲醛浓度分别为0.0817、0.0596 mg/m3。结合图2流场分布图，可以得出，较大的速度能更好地稀释甲醛。自然通风时，衣柜位于窗户邻侧时，甲醛含量明显低于衣柜位于窗户的对侧。该模拟结果与舒爱霞[21]模拟办公室房间内污染源位置对室内甲醛浓度分布的影响结果一致。

图5 特殊截面浓度场分布图

3.4 特殊截面处传质场协同角的分布

传质场协同角的分布如图6所示。模型中x为2.4 m截面处，传质协同角分布较相似，另外2个截面处协同角的分布较不同。由传质过程中的无因次关系式得出，传质区域的速度与浓度梯度的夹角的大小表征了速度场与浓度场的协同程度，当夹角越小时，协同效果越好，对流传质效果越好。而室内通风净化排污过程是宏观的对流传质过程，传质效果越好，净化排污效果越好。对比2模型中3个截面的协同角的分布，x为2.4 m截面处，2模型中的协同角均较另外两个截面的协同角较大，此截面处的速度场与浓度场的协同效果不好，但由于空气的速度较大，其Re数较大，所以传质效果也很好，且甲醛浓度均较低。x为3.9 m截面处两截面的传质协同角有较大差异，模型1中房间上部协同角较下部大，传质效果较好，甲醛扩散效果较好，且在垂直方向上有浓度降低的分层分布。模型2中，房间中间位置的协同角较两侧较大，在房间中间位置的协同角约为120°，甲醛被稀释效果较差。在房间内外侧即靠近墙两侧的协同角约为80°，甲醛在一定程度上被稀释。x为0.9 m截面处，模型2的速度与浓度梯度的夹角明显小于模型1，速度场与浓度场的协同效果更好，模型2中的传质效果更好。并且此截面较另外2个截面的整体传质协同角更小，甲醛被很好地稀释带走。对于卧室，可以更关注于床附近甲醛的净化效果，基于传质场协同原理，可以得出，衣柜摆放如模型2时，床附近的传质协同角越小，速度场与浓度场的协同效果越好甲醛的净化排污效果越好，更利于甲醛的扩散。

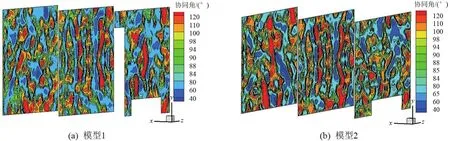
图6 传质场协同角分布

3.5 甲醛含量随高度的变化情况

模型中甲醛浓度随高度的变化如图7所示。靠近地板处，甲醛浓度较高，但在高度方向上由于重力抑制的影响，2条直线中甲醛的含量整体上随高度逐渐降低，在1.0～1.8 m处，甲醛含量有缓慢增加的趋势，高于2 m处，甲醛含量逐渐降低并趋于一定的稳定程度。模型2中甲醛含量明显低于模型1，即污染源衣柜位于窗户的邻侧时甲醛被净化的效果优于污染源衣柜位于窗户的对侧。

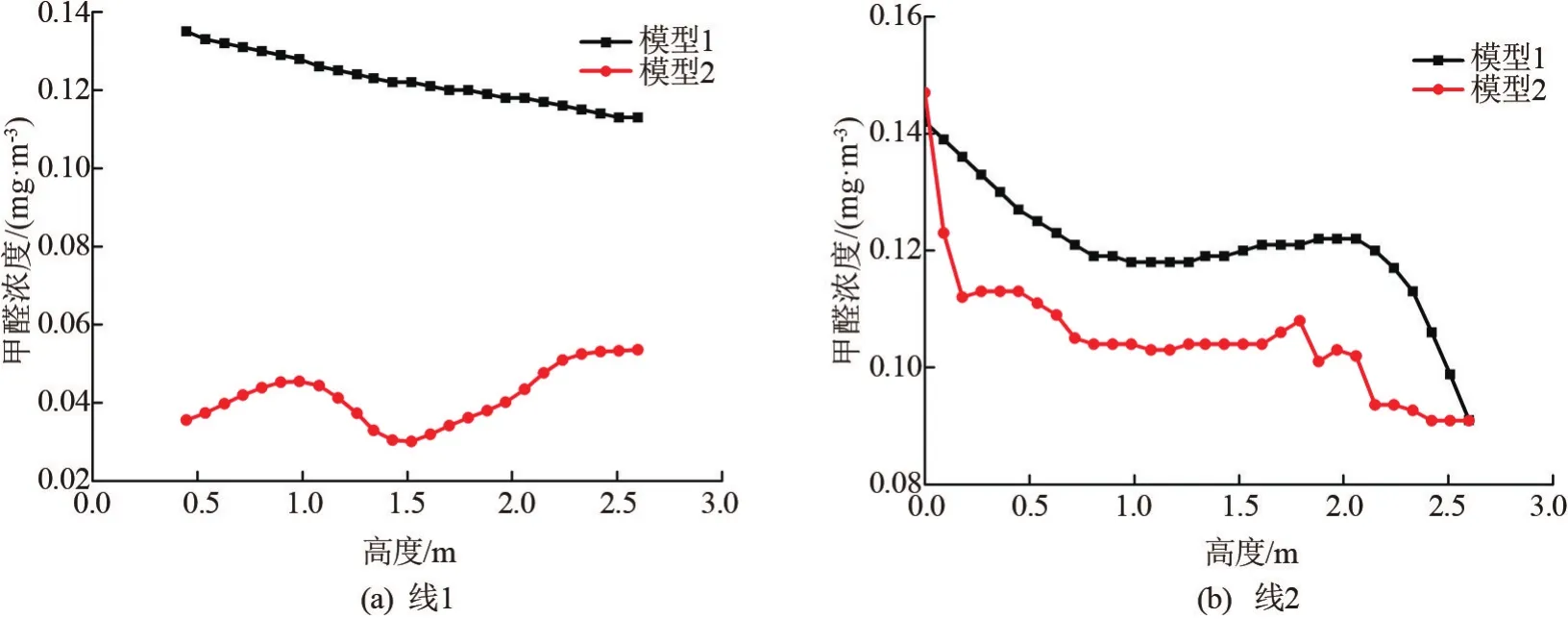
图7 模型中甲醛浓度随高度的变化情况图

3.6 基于场协同理论的结果分析

模型中各截面平均传质协同角的变化情况如图8所示。整体看来，各截面处模型2的传质协同角均小于模型1的。由传质协同角理论得，当速度与质量分数梯度夹角越小时，速度场与浓度场的协同效果越好，传质区域的对流传质效果越好，甲醛稀释扩散过程的效果越好。模型2与模型1由于污染源衣柜的位置不同，使得速度与质量分数梯度的夹角不同，速度场与浓度场的协同效果也不同。

图8 模型中各截面平均传质协同角变化情况图

由图8可以看出，模型中传质协同角均有先减小后增大的趋势，且均在截面1.1 m截面处，传质协同角最小，该截面附近速度场与质量分数夹角最小，速度场与浓度场的协同效果更好，更好地稀释甲醛。x为0.5 m截面处，速度场由于污染源衣柜的约束在此截面处的分布较紊乱，使得此传质区域内的速度场与浓度场的协同效果较差，故两模型中传质协同角最大。x为0.8 m截面处，模型2中的传质协同角较模型1降低了2.37%，而在x为3.9 m截面处，模型2中的传质协同角较模型1中仅降低了0.11%，在x为0.8 m截面处模型2较模型1的速度场与浓度场的协同程度最佳。应用场协同原理更进一步说明了当污染源位于不同位置时，对速度场与浓度场的协同效果有一定的影响，模型2的传质效果优于模型1，更有利于引入的新风对室内甲醛的稀释。

4 结论

文章建立了冬季地板供暖房间的2种物理模型——衣柜位于通风口的对侧(模型1)和衣柜位于通风口的邻侧(模型2)，采用CFD方法及应用传质场协同理论，模拟并分析了在自然通风方式下，室内的流场、温度及甲醛的分布情况。主要结论如下:

(1)室内的流场分布对房间的温度场及甲醛的浓度场影响较大，且房间内甲醛的浓度场与温度场的分布相似。

(2)室内甲醛的分布在竖直方向上有明显的分层现象，在竖直方向上由于重力的抑制作用，随高度的增加，甲醛的含量逐渐降低。甲醛的含量在床附近较高，但模型2的含量明显低于模型1。

(3)当室内空气速度方向与浓度的梯度方向夹角越小时，传质协同效果更好。当通风口位置确定时，即送风速度及方向一定时，污染源位于不同位置时，室内的气流组织影响室内的污染物的浓度分布。当衣柜位于通风口邻侧时，送风速度方向与污染物的浓度梯度的夹角更小，速度场与浓度场的协同效果更好，传质效果更好，将更有利于引入的新风对甲醛的稀释，从而降低室内的甲醛含量，尤其是床附近人员停留区域甲醛平均浓度0.0592 mg/m3，较污染源衣柜位于通风口对侧时甲醛浓度降低27%。