基于Küssner函数的不同气动导纳模型对大跨桥梁抖振响应的影响

张志田， 陈添乐， 吴长青

(湖南大学 风工程试验研究中心，长沙 410082)

桥梁抖振分析有时域和频域两种算法，频域分析具有简单快速的优点，但只适用于线性问题，只能得到结构响应的统计特性。时域分析能考虑各种非线性影响，并能得到抖振位移时程，但不便于气动导纳的灵活应用。抖振时域分析分为以下三个环节：桥梁脉动风场模拟、抖振力的表达、抖振位移计算。脉动风场模拟一般采用谐波合成法，国内外许多学者已对此做过详尽研究[1-4]。抖振力的关键问题是气动导纳函数的确定。自20世纪60年代Davenport将Sears函数和Liepmann的机翼抖振理论应用于桥梁抖振分析至今[5-6]，桥梁颤抖振计算通常采用Davenport准定常模型、气动导纳、以及Scanlan建议自激力表达式[7]。对于气动导纳，文献中通常要么取值为1(即不考虑抖振力的1非定常特性)，要么取Sears函数或者试验导纳[8-11]。但是三种气动导纳计算结果到底有多大的差别是一个值得深入研究的问题。在目前抖振时域计算中，一般是采用等效风谱法进行抖振力的计算[12]，即把气动导纳乘以风谱看成一个等效风谱，再用得到的等效风谱进行脉动风场模拟。等效风谱法是通过修正风谱来间接考虑抖振力的非定常性，当导纳为试验值时，需要分别对升力、阻力、扭矩的等效风速时程进行模拟。故本文放弃采用等效风谱法，而是从气动力演变特性出发采用Küssner函数进行抖振力模拟。并在此基础上分析不同气动导纳模型引起的抖振响应差别。

1 非定常抖振力的卷积表达

以水平速度U飞行的断面，穿过幅值为w0的竖向阶跃阵风时，其气动力随时间演变的公式为[13]

(1)

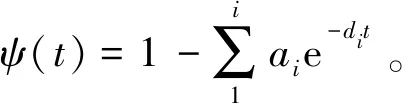
(2)

式中：a0,ai,di为常数。

文献[14-15]中指出式(2)中的a0项应该等于1，本文抖振力表达式最终是要和Scanlan建议抖振力模型进行功率谱等效，故不详细讨论其所代表的物理意义。

在线性叠加原理满足的前提下，任意分布的竖向脉动风w(t)引起的非定常气动升力可表示为

(3)

式中：ψ′(σ)为Küssner函数对时间t的导数。

式(3)中只考虑了竖向脉动风的影响，在桥梁风工程中，同时考虑水平向和竖向脉动风所引起的非定常气动力为

(4)

(5)

(6)

式中：C′L,C′D,C′M分别为升力系数、阻力系数和升力矩系数对攻角的导数； 函数ψFx(F=L,D,M;x=u,w)表示x方向的单位数值脉动风引起的每延米F气动力的瞬态演变，都为Küssner类型的函数；ψ′Fx(F=L,D,M;x=u,w)为Küssner函数对时间t的导数；ψFx表达式如下

(7)

2 Küssner函数的拟合

断面气动导纳函数已知的情况下，引入气动导纳修正的Scanlan建议抖振力模型如下[16-17]

(8)

(9)

(10)

式中：CL,CD,CM分别为升力系数、阻力系数和升力矩系数；χLu,χLw,χDu,χDw,χMu,χMw为6个气动导纳。

根据式(8)～(10)，求得抖振力功率谱如下

(11)

(12)

(13)

式中：SL,SD,SM分别为升力、阻力、升力矩的功率谱；Suu,Sww分别为水平和竖向的脉动风功率谱；Suw,Swu为脉动风互功率谱；式中*号表示求复共轭。

同样，对本文中采用Küssner函数表示的抖振力表达式(4)～(6)求得抖振力功率谱如下

(14)

(15)

(16)

式中的-号表示求傅里叶变换。

根据两种抖振力表达式功率谱相等的原则，忽略互功率谱的影响，分别比较式(11)与式(14)，式(12)与式(15)，式(13)与式(16)，可以得到如下关系

(17)

(18)

(19)

(20)

(21)

(22)

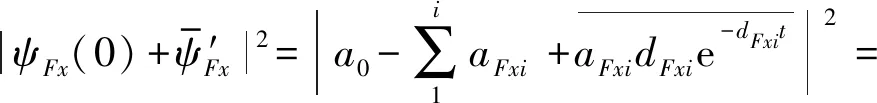
(23)

式中：ω位脉动风的圆频率。

将式(23)代入式(17)～(22)中得到各Küssner函数参数与气动导纳的关系后，可根据已知的气动导纳确定Küssner函数参数。这是一个最优化问题，可以通过以下六个函数的极小值问题求得所需结果

(24)

(25)

(26)

(27)

(28)

(29)

式中： 求和符号上标n为气动导纳试验点(不同的折算频率K)的数目。

根据式(24)～(29)就能识别得到与水平以及竖向脉动风相关的升力、阻力和升力矩6个Küssner函数的待定参数，需要说明的是参数拟合过程中可能存在多个折算频率点，即存在很多拟合点，为此作者使用遗传算法进行参数拟合[18]，在设定初始种群、适应度函数以及控制参数后，遗传算法会对每一次进化后的种群进行计算，使式(24)～式(29)的值最小的一些个体称为优异个体，下一次进化时优异个体会得以保留，其它个体在会淘汰或者变异，将进化后的种群代入式(24)～式(29)重新计算。随着种群的进化，最终优异个体会越来越多，直至产生满足设定条件的个体。

3 抖振时域分析

求出升力、阻力和升力矩的Küssner函数表达式后，可采用式(4)～式(6)对结构进行动力有限元抖振分析。但由于式(4)～式(6)中存在与脉动风速相关的时间积分，直接使用其求解抖振力的计算效率非常低。参考文献[14-15]的时域自激力递推表达式可得到抖振力的递推表达如下：

首先，将抖振力分解成脉动风u、v两部分的贡献之和

(30)

(31)

(32)

式中：Fbu(t),Fbw(t)(F=L,D,M)分别为顺风向和竖风向脉动风速引起的抖振力(升力、阻力和升力矩)。以式(30)中顺风向脉动风速引起的抖振升力Lbu(t)为例进行如下推导，对积分项中进行变量代换后得

(33)

式中：

(34)

由式(33)可知，对于任意时刻的抖振力，第一项只与当前时刻的风速有关，而第二项则为时间积分项，与整个时间历程风速有关，故根据t时刻的抖振力表达式递推得到t+Δt时刻的抖振力，只需要求式(34)的递推表达即可，该式的递推表达如下

(35)

同理可得到其它几个抖振力的递推表达式

(36)

(37)

(38)

(39)

(40)

4 数值算例

以某特大悬索桥的初步设计方案为例，计算其在0°风攻角下的抖振位移响应。该桥为主跨920 m的单跨扁平钢箱梁悬索桥，主塔采用混凝土浇筑，共设75对吊杆，桥址位于我国西南部山区峡谷，受脉动风影响较大。该桥立面图和箱梁断面，如图1与图2所示。

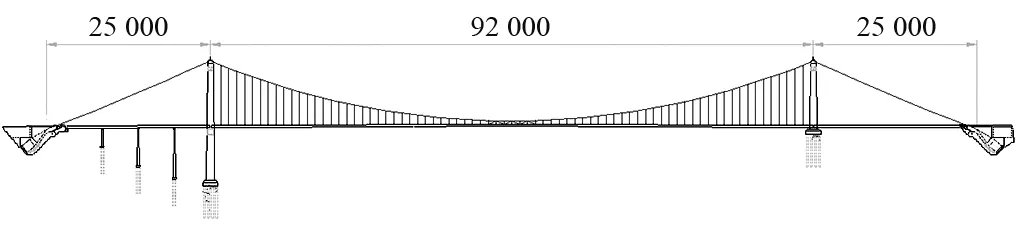
图1 悬索桥立面图(cm)Fig.1 The elevation of the suspension bridge(cm)

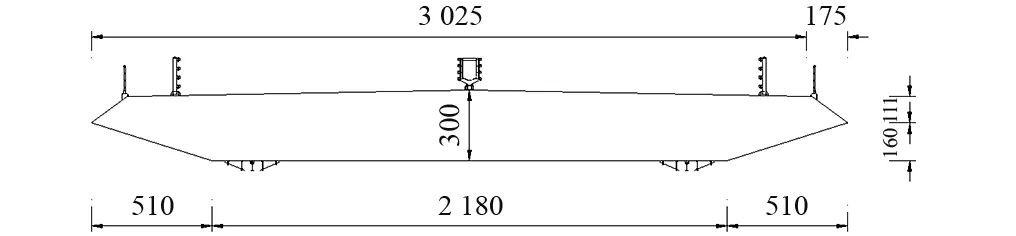
图2 桥梁箱梁断面(cm)Fig.2 Section of the box girder(cm)

4.1 三分力系数和气动导纳试验值

采用几何缩尺比为1∶50的主梁节段模型进行风洞试验。模型的长度为1.54 m，宽度为0.64 m。模型本身具有足够大的刚度，测力试验以及气动导纳试验中无出现明显变形。三分力试验采用高频测力天平测得试验风速下不同风攻角的静力三分力，通过计算得到该断面的三分力系数以及三分力系数对攻角的导数。气动导纳测试时采用水平格栅产生被动紊流。三分力试验以及气动导纳试验的风洞布置分别见图3(a)与3(b)。通过风洞试验测得0°攻角时的三分力系数为CL=-0.190 7，CD=0.029，CM=0.008 5，三分力系数对攻角的导数为C′L=3.095 1，C′D=0.280 2，C′M=1.057 1。

图3 风洞试验Fig.3 Wind tunnel tests

气动导数的识别方法主要有等效导纳法、交叉谱法以及自功率谱-交叉谱总体最小二乘法。等效导纳法是基于抖振力功率谱识别导纳，需要假设顺风向导纳与竖风向导纳相等[19]；交叉谱法通过求气动力和脉动风速的交叉谱来识别气动导纳[20]，自功率谱-交叉谱总体最小二乘法是结合上述两种方法，采用最小二乘法识别气动导纳[21]。此外，对于存在分享流的钝体桥梁断面，气动导纳并非仅仅由气动外形以及频率决定，同时也受来流的湍流特性的影响，即不同的风场特性会产生不同的气动导纳[22]。本文关注的侧重点不是气动导纳的识别方法以及不同识别方法所带来的差异，因此这里采用最简单也最稳定的等效导纳法识别法。等效导纳法假设χL=χLu=χLw,χD=χDu=χDw,χM=χMu=χMw[19], 将其代入式(11)～式(13)中，忽略互功率谱的影响可得

(41)

(42)

(43)

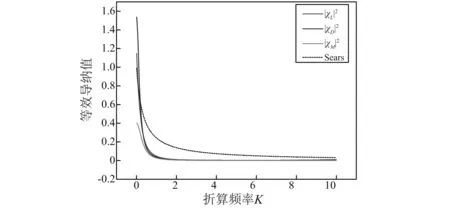
图4 等效气动导纳试验值Fig.4 The test value of equivalent aerodynamic admittance

4.2 Küssner函数参数拟合

在Küssner函数的拟合过程中，本例中指数项取三项，需要拟合的参数为7个，采用遗传算法进行参数拟合时种群规模取为5 000，每一代的精英数目为300，交叉概率取0.8，变异率取0.1，停止条件为容许误差小于0.000 1。表1和表2分别列出了Sears函数和试验气动导纳的各Küssner函数参数拟合值。

表1 Sears函数的Küssner函数参数拟合值Tab.1 Fitted value of Sears function of Küssner function

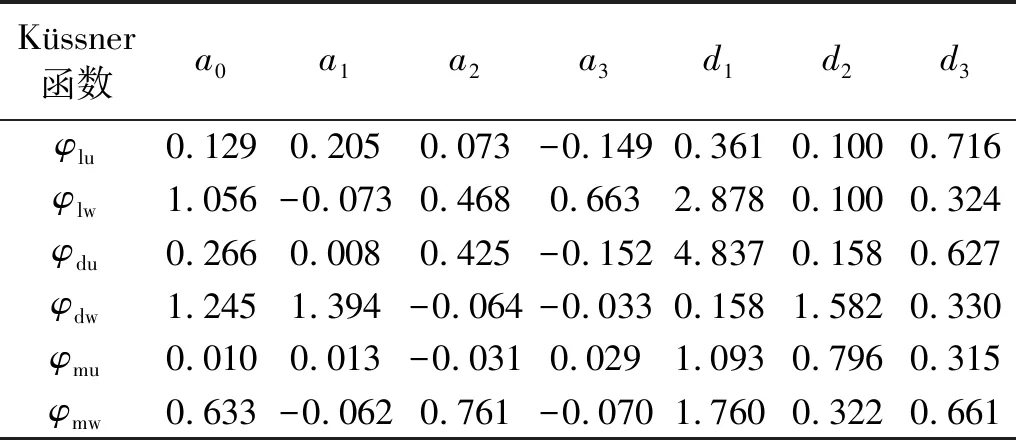
表2 试验导纳的Küssner函数参数拟合值Tab.2 Fitted value of test admittance of Küssner function

将拟合得到的Küssner函数代入式(17)～式(22)中，可以反算出气动导纳拟合值，图5给出了Sears函数拟合值与Sears函数的比较，图6给出了试验气动导纳拟合值与试验值的比较。从图5和图6可以看出，不论是Sears函数还是试验气动导纳，反算得到的气动导纳与目标值都具有很高的吻合度。因此，本文的抖振力模型与引入气动导纳修正的Scanlan建议模型两者的抖振力功率谱是等效的。

图5 Sears函数拟合值与Sears函数的比较Fig.5 Comparison of fitted Sears with Sears function

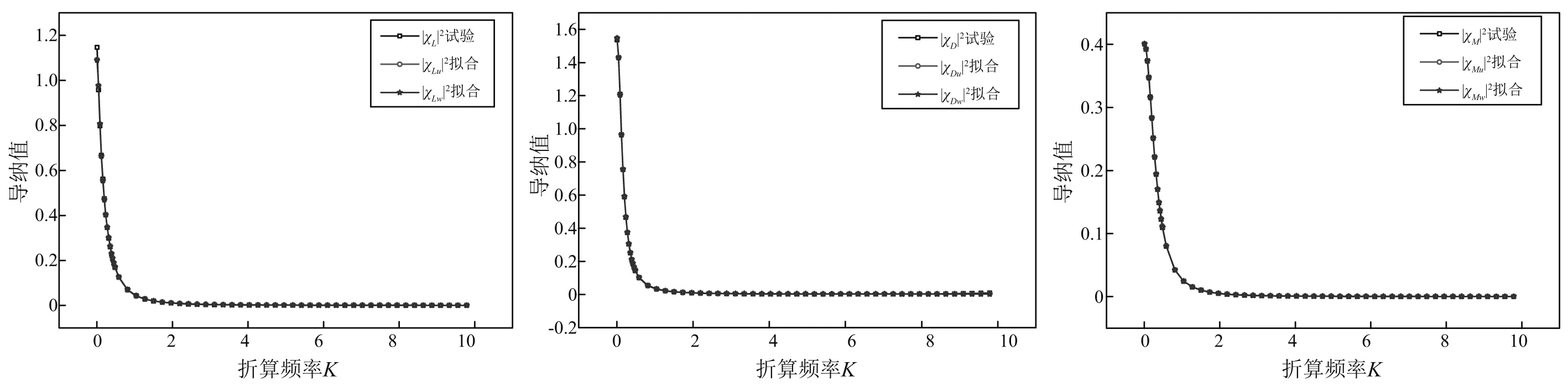
图6 试验导纳拟合值与试验导纳的比较Fig.6 Comparison of fitted equivalent aerodynamic admittance with test values

4.3 脉动风场模拟

本文的风场模拟中，顺风向和竖风向风谱分别采用Kaimal谱、Panofsky谱[23-24]，风场模拟采用谐波合成法，具体过程已有学者做过详细研究，在此不再赘述。需要说明的是本文主要是研究不同气动导纳对桥梁抖振响应的影响，因此在合成功率谱密度矩阵时，无需讨论衰减因子λ取值对脉动风速时程的影响，本文中取值为λ=7，且风速时程取为600 s。表3给出了风场模拟的主要参数。图7、图8分别为跨中处模拟的顺风向和竖风向脉动风速时程，图9、图10分别为对应的脉动风速功率谱和目标功率谱的比较。

表3 风场模拟的主要参数Tab.3 Main parameters of the wind field simulation

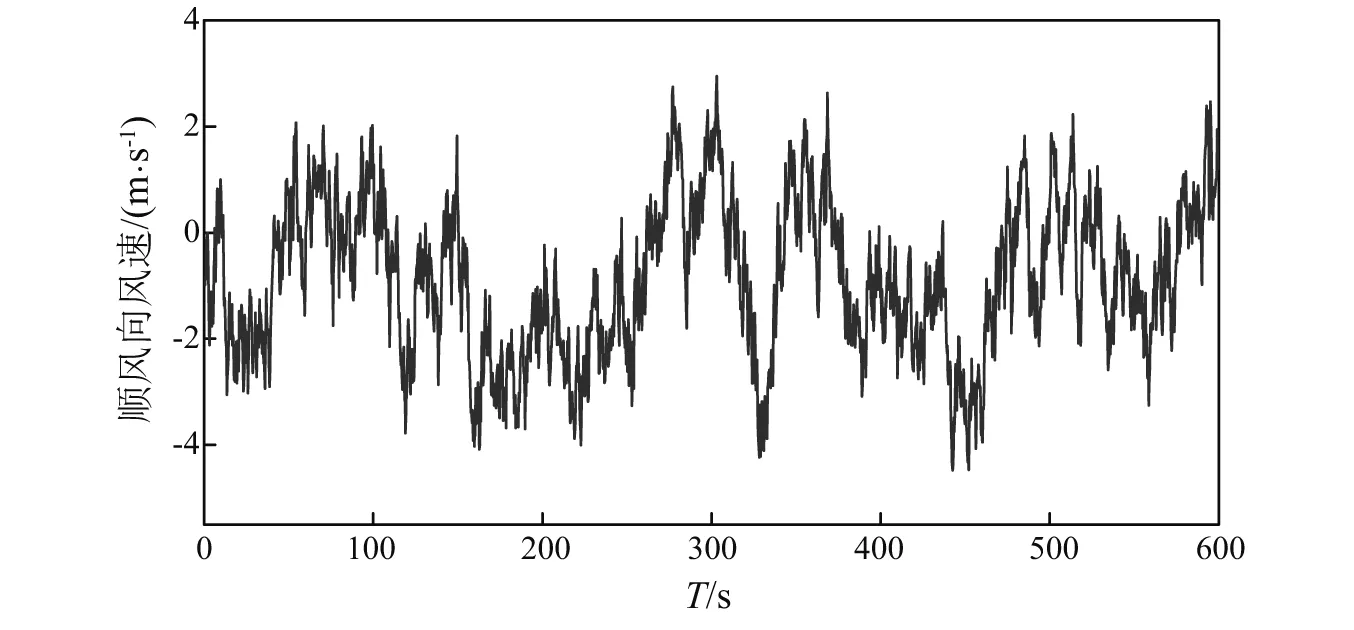
图7 跨中处顺风向脉动风速时程Fig.7 Time history of fluctuating wind velocity of the mid-span section

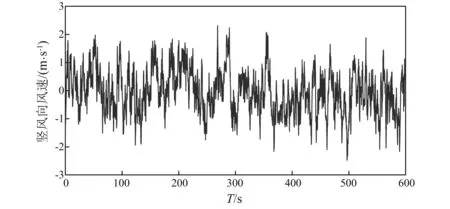
图8 跨中处竖风向脉动风速时程Fig.8 Time history of vertical wind velocity of the mid-span section

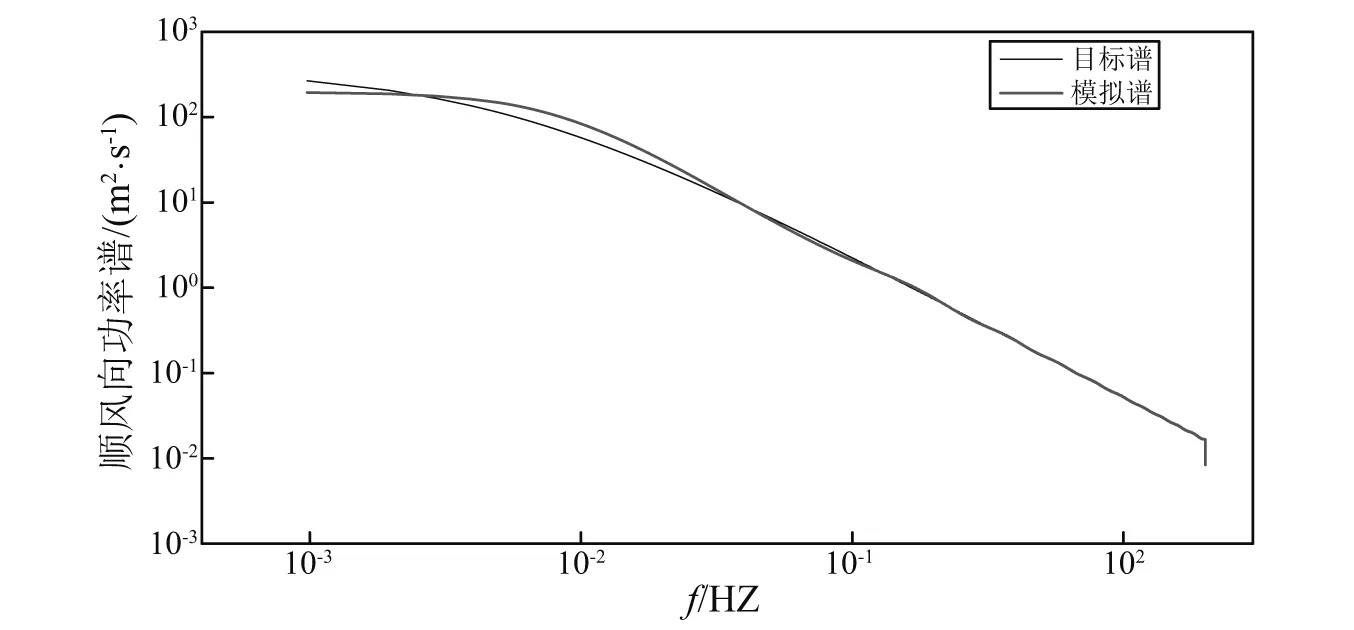
图9 跨中处顺风向脉动风功率谱密度Fig.9 The power spectral density of fluctuating wind of the mid-span section

4.4 抖振力计算

“4.3”中已经说明本文主要目的是研究不同气动导纳对桥梁抖振响应的影响，因此在动力有限元计算时，荷载只考虑了抖振力。

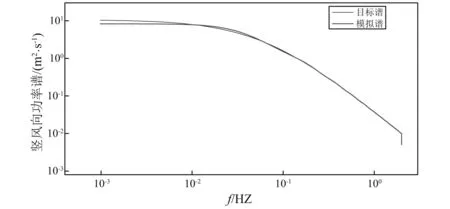
图10 跨中处竖风向脉动风功率谱密度Fig.10 The power spectral density of vertical wind of the mid-span section

对气动导纳等于1即不考虑气动导纳的情况，直接采用准定常模型计算得到抖振力时程；对于考虑气动导纳修正的情况，采用本文推导的抖振力递推表达式计算。将Sears函数的Küssner函数参数拟合值与模拟脉动风速时程带入本文抖振力递推表达式中，得到考虑Sears函数修正的抖振力时程；同样，将试验气动导纳的Küssner函数参数拟合值与模拟脉动风速时程带入递推表达式中，得到考虑试验气动导纳修正的抖振力时程。至此，已获得考虑不同气动导纳影响抖振计算所需的三组抖振力。跨中处不同气动导纳计算得到的抖振力时程，如图11所示。

4.5 本文küssner表达式抖振位移计算结果与分析

图12为跨中处不同气动导纳函数计算得到的抖振位移时程，根据图10可知，不同气动导纳计算得到的抖振位移响应时程在变化趋势上大体一致，但是响应大小有明显差别。对于本例中3种抖振位移响应，考虑气动导纳修正的抖振位移远小于不考虑导纳修正的位移；导纳为1时计算得到的抖振位移最大，试验气动导纳修正计算得到的抖振位移最小，Sears函数修正的结果位于导纳为1和试验导纳计算结果之间。

图13更清楚地反应了不同气动导纳引起的抖振位移的差别。①对比导纳为Sears函数和导纳为1时的情况，竖向位移均方根前者比后者小了32.4%；扭转位移均方根前者比后者小了45.2%；侧向位移均方根前者比后者小了50.1%。②对比导纳为试验值和导纳为1时的情况，竖向位移均方根前者比后者小了35.2%；扭转位移均方根前者比后者小了66.3%；侧向位移均方根前者比后者小了65.8%。③本例中三种抖振位移响应均方根，考虑气动导纳修正的结果均小于气动导纳为1的情况，且气动导纳为试验值的结果最小。④Sears函数对不同的抖振位移响应均方根影响程度不一样，Sears函数对侧向位移响应的均方根影响最大，对竖向位移响应的均方根影响最小。⑤试验导纳对侧向和扭转位移响应的均方根影响较大，对竖向位移响应的均方根影响最小。

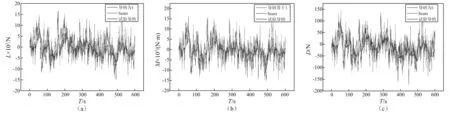
图11 跨中处的抖振力时程Fig.11 Time history of buffeting force of the mid-span section

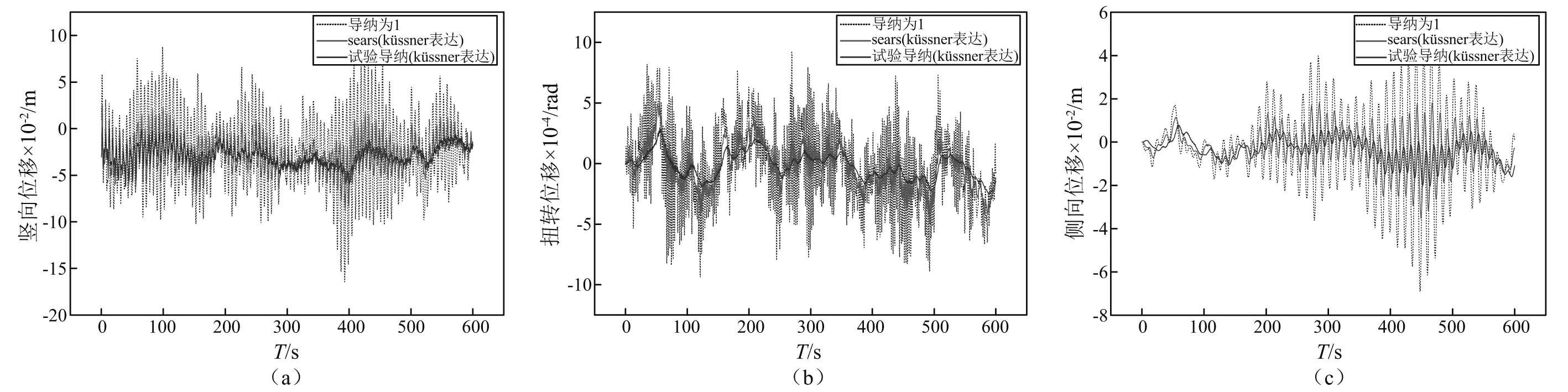
图12 跨中处的抖振位移时程(küssner表达)Fig.12 Time history of buffeting response of the mid-span section(by küssner expression)

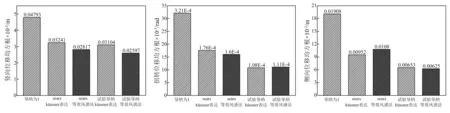
图13 跨中处的抖振响应均方根Fig.13 RMS of buffeting response of the mid-span section

图14为跨中处不同气动导纳函数计算得到的位移功率谱密度，本算例中竖向位移功率谱第一个峰值横坐标为0.171 8，与结构一阶正对称竖弯自振频率(0.174 5)相对应，扭转位移功率谱第一个峰值横坐标为0.403 3，与结构一阶正对称扭转自振频率(0.401 9)相对应，侧向位移功率谱第一个峰值横坐标为0.083，与结构一阶正对称侧弯自振频率(0.082 9)相对应。位移功率谱密度最大值均出现在第一个峰值处。

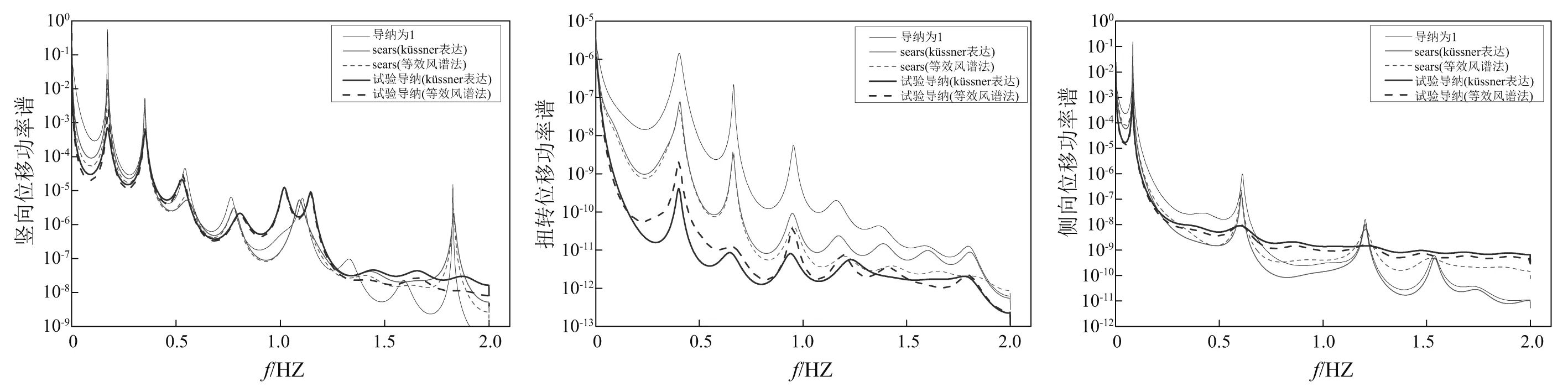
图14 跨中处抖振位移功率谱密度Fig.14 The power spectral density of buffeting response of the mid-span section

从图14可以发现： ①抖振位移响应主要是受若干阶低频模态的控制，尤其是受基频的影响最大。②在主要频率范围内，导纳函数为1时位移响应功率谱密度最大，Sears其次，试验导纳的位移功率谱密度最小。这与抖振位移时程的结论是一致的。

4.6 本文küssner表达式法与等效风谱法的比较

通常采用等效风谱法进行考虑气动导纳修正的抖振时程计算，即把气动导纳函数乘以风谱看成等效风谱，然后用等效风谱进行脉动风场模拟。本小节中首先得到考虑sears函数和试验导纳函数修正的等效风谱，再采用和“4.3”节中相同的参数进行脉动风场模拟。对于试验气动导纳修正的情况，由于升力、扭矩和阻力的导纳函数不同，需分别模拟升力、扭矩、阻力的顺风向和竖风向共6组脉动风速时程。

图15为等效风谱法计算得到的跨中抖振位移时程，与图14中的Küssner方法所得结果相比可以发现：①定性结果一致，即考虑sears函数修正的抖振位移小于不考虑修正结果，考虑试验导纳修正的抖振位移小于sears函数修正结果。②两者计算得到的随机抖振位移的变化范围基本一致。③本文中采用Küssner函数时采用同一组脉动风速时程，不同导纳计算的抖振位移随时间变化具有同步性；而采用等效风谱法时，不同的导纳函数和抖振力均需要单独模拟脉动风时程，因而不同导纳计算的抖振位移随时间变化无同步性。

图16为分别采用Küssner表达式和等效风谱法计算得到考虑sears函数修正的跨中抖振位移时程，可见虽然两者抖振位移随时间变化并不一致，但是两者的变化范围基本相同。

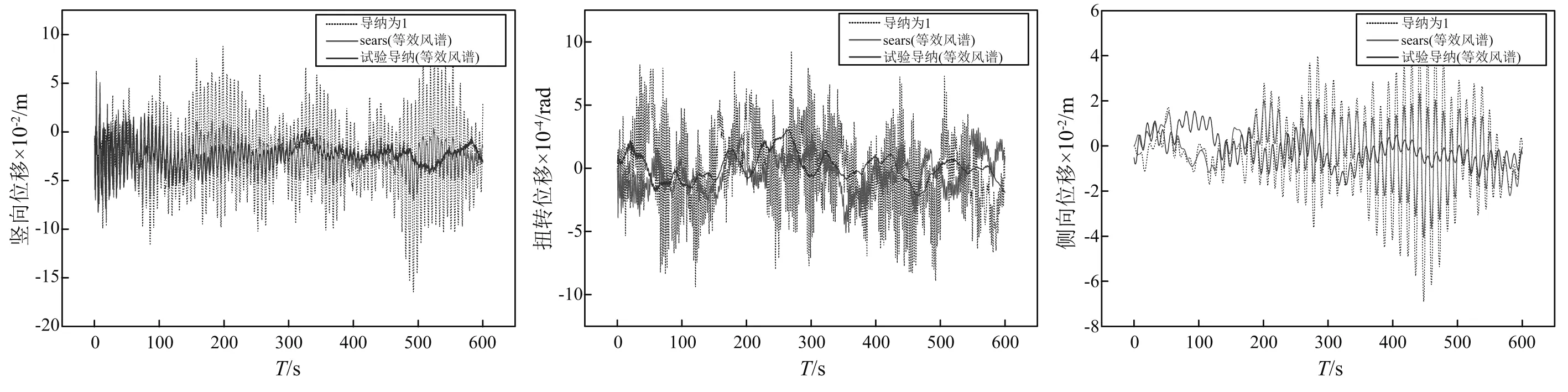
图15 跨中处的抖振位移时程(等效风谱法)Fig.15 Time history of buffeting response of the mid-span section(by the equivalent wind spectrum)

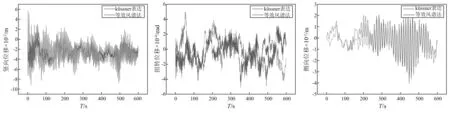
图16 跨中处Küssner表达式和等效风谱法计算得到的考虑sears函数修正的抖振位移时程Fig.16 Time history of buffeting response of the mid-span section calculated by Küssner expression and equivalent wind spectrum method which sears function is modified

图13比较了本文Küssner表达式和等效风谱法计算得到的抖振响应均方根。①导纳为sears函数时，竖向位移两者计算相差13.1%，扭转位移相差9.1%，侧向位移相差 11.8%。②导纳为试验值时，竖向位移两者计算相差16.3%，扭转位移相差2.7%，侧向位移相差 4.3%。两种方法在计算竖向位移均方根时相差较大，作者认为主要原因有两方面：其一是有限长度的风场模拟时存在个体差异；其二是两种方法形成的抖振力相关谱不等效。

5 结 论

扁平钢箱梁是大跨度桥梁常用的加劲梁型式。由于其良好的气动外形与平板具有一定的相似性，对这类桥梁进行抖振分析时常采用源于古典机翼理论的Sears气动导纳函数代替断面的实际气动导纳函数，或者偏于安全不考虑气动导纳函数。桥梁抖振分析的传统方法有频域与时域两类方法。频域法可方便地考虑气动导纳，但忽略了结构的非线性；时域法能全面考虑非线性，但不便于气动导纳的应用。本文基于Küssner函数时域模型，在时域内研究了这三种不同的导纳选取方案对千米级桥梁抖振分析结果的影响，并得到以下结论：

(1) 本文提出Küssner阶跃函数法可将气动导纳灵活地从频域转换到时域后进行非线性动力有限元分析。

(2) 与等效风谱法相比，本文的Küssner函数时域抖振模型只需模拟一组脉动风速时程，提高了计算效率。此外，应用于实测风速时程时，避免了根据时程反算风谱、风谱等效后再模拟时程的繁琐过程。

(3) 基于Sears函数气动导纳与试验气动导纳得到的竖向响应基本一致，但扭转与侧向响应相差明显。以扭转响应为例，前者在后者的基础上高出约63%。显然，即使是扁平钢箱梁，采用源于机翼理论的Sears函数进行抖振分析不合适。