菱形颗粒冲击延性材料的运动行为及凹坑形态研究

杜明超， 李增亮， 董祥伟， 孙召成， 范春永， 车家琪

(中国石油大学 (华东)机电工程学院，山东 青岛 266580)

微小杂质颗粒(微米至毫米量级)冲击材料表面导致材料去除的现象广泛存在于许多工程领域中，例如冲蚀磨损[1]，射流破岩[2]，喷砂清理[3]等。该过程既可以是有益的，也可能是有害的。颗粒冲击材料表面属于双体碰撞问题，其破坏行为取决于冲击速度、冲击角度、颗粒形状及尺寸、材料的类型等因素，可导致材料表面产生微小划痕(凹坑)、微切削、颗粒破碎、颗粒嵌入等现象。研究者们针对颗粒冲蚀现象进行过许多研究，例如Azimian等[4]建立模拟夹杂颗粒的固液流场环境，结合冲刷实验研究了冲蚀磨损问题。但是其主要关注一定冲刷时间所造成的冲蚀宏观效应，并未从颗粒微观的角度，研究颗粒撞击微观过程。

Finnie[5]最早从单个颗粒冲击入手，研究角型颗粒撞击导致的材料变形行为，分析了角型颗粒在冲击过程中对塑性材料的“切削”机制，假定颗粒在碰撞过程中不产生变形，建立了冲蚀理论模型，其适用于颗粒硬度远高于靶体和低速撞击的情况。Hutchings等[6-7]改进了Finnie模型，考虑了颗粒在碰撞过程中的自由旋转，研究了单个方形颗粒冲击韧性金属材料表面导致塑性变形特征以及颗粒的反弹行为。同时，Hutchings发现角型颗粒在撞击过程中的旋转对颗粒的冲蚀机制有很大的影响。Papini及其研究团队[8-9]采用气动发射装置研究对称形状的角型颗粒在射速30～100 m/s的入射速度下的冲蚀机理，并开发了数值计算模型辅助实验研究，但其研究仍局限在“刚-塑性”假设的框架之内。

近年来，计算流体力学(Computational Fluid Dynamics, CFD)的发展为研究磨料射流、射流破岩以及冲蚀磨损中涉及的固液两相流问题提供了有效的数值模拟手段。国内外学者开始采用CFD模拟方法对相关过程进行研究。Babets等[10]将水和空气作为连续相，磨料颗粒作为分散相，采用VOF模型处理连续相，采用拉格朗日(Lagrangian)方法跟踪颗粒相，得出流场中颗粒轨迹等参数的变化规律。Ahmed等[11]将磨料颗粒、空气和水都作为连续相，采用Euler方法对其进行处理，借助于商业CFD软件研究了混和腔内磨料颗粒入射角和入射位置对准直管喷嘴出口处各相速度分布的影响。高激飞等[12]采用双流体模型，计算了实验室条件下模拟深水域环境淹没磨料射流流场，得到了淹没条件下固液两相射流的速度与压力分布规律，并与实验结果进行了对比。陆朝晖等基于VOF模型和动网格技术建立了截断式脉冲射流的两相流瞬态计算模型，研究了射流流体结构的动态演变特征，并与常规圆柱射流进行了对比。基于CFD的数值模拟方法是从固液两相流场入手，分析固相在流场中的分布，从而得到固相对壁面的冲刷参数，但是再计算冲蚀速率或冲蚀量时，需要借助已有的经验或半经验的冲蚀模型。

本文借助ABAQUS商业仿真软件，建立了菱形颗粒冲击延性材料的冲蚀磨损耦合数值模型，研究单个菱形颗粒冲蚀磨损过程的运动行为及产生的凹坑轮廓形态，并通过重现参考文献[9]中的实验过程验证了该模型的准确性，随后针对6组不同冲击角与方位角的组合研究了冲击速度对颗粒运动行为及凹坑轮廓的影响，充分了解冲击速度对冲蚀磨损过程的影响情况，为后续冲蚀机理的研究打下基础。

1 FEM-SPH模型

1.1 FEM模型

固体力学中的数值模拟方法如有限元法(FEM)可用于颗粒与壁面碰撞过程的模拟。以往的关于微小颗粒冲击问题的研究大多将颗粒假定为球形，引入变形本构方程描述基底的变形行为，能够完整重现颗粒冲击、破坏材料的动态过程，并可实现冲蚀量的定量计算。但FEM并不适合于角型颗粒，这是因为角型颗粒冲击可造成材料的局部大变形甚至脱落，从而导致网格扭曲等问题，影响数值计算稳定性。此外，FEM迭代时间步长由最小单元尺寸控制，网格极度扭曲会加大计算机CPU耗时，降低工作效率。通过采用自适应网格重构或单元失效等方法可解决上述问题，但自适应网格重构法不能添加失效模型，只适合颗粒前旋冲击造成的材料堆积情况。其次，计算效率低，每次迭代会重新生成网格，导致整个数值计算过程容易出现错误。单元失效法是一种自动删除扭曲大变形单元的方法，对不同形状颗粒适用性不同，对尖角菱形颗粒适用性较好，对钝角方形颗粒适用性差。实验中颗粒对工件的“犁耕”作用会在工件表面产生材料堆积，仿真模拟中材料堆积处网格单元变形过大被删除[13]，与物理实际相悖。因此，无网格拉格朗日方法为角型颗粒冲蚀计算提供了另一种解决方案，如SPH方法[14-17]、离散单元法[18](Discrete Element Method, DEM)方法等。

1.2 SPH模型

光滑粒子流体动力学法(Smoothed Particle Hydrodynamics, SPH)是一种无网格(自由网格)的数值计算方法，该方法通过一系列粒子代替网格法中的节点和单元(这些粒子即是计算域中的积分点)，对目标区域进行离散化处理，本质上是一种自适应拉格朗日粒子法。SPH方法中的粒子携带所有计算信息，能够在空间运动，形成了求解描述连续性流体动力学守恒定律的偏微分方程的计算框架。

SPH方法中网格单元被粒子代替，不会出现网格畸变和扭曲缠绕等问题，但边界区域的处理是SPH方法中一个重要的问题。由于缺少相邻粒子，标准SPH方程无法求解边界层粒子的运动方程，为解决该问题， Randles等[19]和Vilad等[20]提出了一种重整化SPH方程，不仅适用于边界层粒子，也适用于无规则扰动粒子；此外，SPH计算过程耗时长，CPU负荷大，单核运算影响工作效率。

1.3 FEM-SPH模型

由于微小颗粒冲击的持续时间非常短暂，且时间尺度会随着颗粒尺寸的降低而降低，在单颗粒实验中一般使用放大尺寸的颗粒(通常大于1 mm)。因此，有必要引入数值方法来辅助实验研究更低尺度的颗粒冲击问题。ABAQUS 6.14是一款功能强大的工程模拟有限元(FE)软件，在动态显示求解下，其网格属性模块可将网格单元转化成无网格粒子，用于模拟材料大变形及冲击载荷的实验工况。本文采用FEM-SPH耦合方法，采用多处理器并行运算和重整化SPH方程求解，同时解决了FEM和SPH方法的局限性。

颗粒冲击金属表面的特征参数定义如图1所示，vi为初始冲击速度，αi为冲击角，θi为初始方位角，θi0为初始旋转角，vr,αr,θr分别定义为颗粒的反弹速度，反弹角和反弹方位角。A定义为菱形颗粒的菱角度，h为颗粒棱长，w为颗粒厚度，本文中实验和仿真的数值为：A=60°，h=5.46 mm，w=3.2 mm。

图1 颗粒特征参数的定义Fig.1 Particle with its characteristic parameters

本文针对Takaffoli和Papini等的实验对菱形颗粒高速冲蚀过程建立了数值模型，如图2所示。由图2可知，在FEM-SPH耦合模型中，只有冲击后发生材料大变形的区域被离散成无网格粒子，剩余区域以及菱形颗粒仍然离散成有限元网格单元。SPH模块和FE模块是通过ABAQUS中tie约束命令耦合在一起。颗粒与金属表面通过罚定义接触，为提高仿真结果与实验结果的吻合度，金属表面动摩擦因数设为0.1，模型底部完全约束，侧面设置关于X-Z平面和Y-Z平面的对称约束，冲击颗粒约束为刚体，被冲击金属材料为OFHC copper，材料参数，如表1所示。

2 材料模型

2.1 状态方程(EOS)

固体颗粒冲蚀金属材料是一个瞬时大变形过程，

图2 FEM-SPH耦合模型Fig.2 Coupled of FEM-SPH

材料属性符号数值密度/(kg·m-3)ρ08 960剪切模量/GPaG47.7泊松比υ0.34熔融温度/KTm1356参考温度/KTr294比热/(J·(kgK))CP383J-C初始屈服应力A90 MPaJ-C应变强化系数B292 MPaJ-C硬化指数n0.31J-C应变率强化系数C0.025J-C热软化指数m1.09

颗粒冲击瞬间的动压远远超过材料本身的屈服极限，状态方程(ESO)通过定义静压、密度和比能之间的关系，可完整描述被冲击材料的动态响应过程[21]。冲击状态方程是用于描述固体碰撞的数学方程，需通过动载实验测出颗粒速度(Up)和冲击速度(Us)。对于大多数固体和流体而言，在一定压力范围内，颗粒速度(Up)和冲击速度(Us)呈线性关系，但在高速冲击条件下，颗粒速度(Up)和冲击速度(Us)的关系表现为非线性，对非金属材料尤为明显。ABAQUS中嵌入了Mie-Gruneisen状态方程，通过输入OFHC copper材料的Mie-Gruneisen参数可定义被冲击金属材料的动态响应过程，OFHC copper材料的Mie-Gruneisen参数，如表2所示。

表2 OFHC copper的Mie-Gruneisen参数Tab.2 M-G parameters of OFHC copper

2.2 Johnson-Cook本构模型

(1)

式中： 无量纲化塑性应变率和温度定义如公式(2)、式(3)所示。

(2)

T*=T-Tr/Tm-Tr

(3)

式中：ε0是参考等效塑性应变率，Tm和Tr分别为熔融温度和参考温度，A，B，C，m，n是材料参数，由实验获得，其中参数A，B，n描述了材料屈服应力与应变率和机械硬化之间的关系，参数C和m描述了材料应变率和热软化敏感度。本文实验选用的颗粒材料为W18Cr4V，工件材料为OFHC copper，Johnson-Cook的材料参数，如表1所示。

2.3 失效模型

颗粒后旋冲击运动对金属表面产生机加工，出现材料切屑分离和剔除现象，为模拟金属材料的失效行为，需要引入失效模型。本文采用基于Johnson-Cook塑性模型的失效模型，当方程(4)中破坏参数Di=1[23]时，失效发生，SPH粒子单元i标记失效并从模型表面去除。

D=ΣΔε/εf

(4)

式中： Δε是积分周期内粒子塑性应变的增量，通过计算每个粒子的累积塑性应变增量，得到(ΣΔε)i，εf为材料的失效应变，该失效模型考虑了机械硬化、黏性应变率以及材料热软化的影响，其函数方程如公式(5)所示。

(5)

式中：σp为主应力，σe为等效应力，T为材料基体温度，d1，d2，d3，d4，d5是Johnson-Cook失效模型的5个参数[24]，由实验测试得出，具体数值见表3。

表3 OFHC copper中Johnson-Cook失效模型参数Tab.3 Johnson-Cook failure model parameters for OFHC copper

3 结果和分析

3.1 模型验证

为验证FEM-SPH耦合模型的准确性，首先进行了仿真验证实验。表4给出了Takaffoli和Papini等的原始实验数据，包括初始实验条件和测得实验参数。表4中case2、3的颗粒为前旋旋转(顺时针)，反弹角小于90°，颗粒向前反弹；case4、6、7、9、10中颗粒为后旋旋转(逆时针)，反弹角小于90°，颗粒向前反弹；case1、5中颗粒为后旋旋转(逆时针)，反弹角大于90°，颗粒向后反弹；case8为特殊工况，颗粒由后旋旋转转变为前旋旋转。保证初始实验条件不变，进行了与实验一一对应的仿真模拟，测量出仿真模拟中颗粒的反弹速度(vr)，反弹角度(αr)，凹坑周围材料堆积高度dmax以及凹坑最大深度hlip，如表5所示。对比表4和表5可知，除case4，其它工况中实验结果与仿真结果高度吻合。case4中实验结果出现切屑分离，但仿真模拟并未出现，原因之一是该工况下实际冲击速度可能大于测量值，随着仿真模拟中入射速度的增加，切削分离现象出现。

表4 实验数据Tab.4 Experimental data

表5 仿真模拟预测数据Tab.5 Simulation predicted data

图3展示了case1、2、8颗粒运动轨迹的实验结果和仿真结果，实验结果图片取自文献[9]，由高速摄像机抓拍获得，仿真结果取自本文FEM-SPH耦合模型。对比实验结果和仿真结果可以看出，该耦合模型能够很好地捕捉冲蚀磨损过程菱形颗粒的运动行为，3种工况下颗粒运动轨迹的实验结果与仿真结果吻合度较高，并能够重现冲蚀磨损过程中颗粒的前旋旋转和后旋旋转行为。

图3 模型验证Fig.3 Model validation

冲蚀磨损过程颗粒角速度随时间的变化规律如图4所示，其中case1、6、10为后旋旋转，case2为前旋旋转，case8为后旋向前旋转变(注：转变只能从后旋向前旋转变)。图5展示了case2和case6中实验测得的凹坑轮廓与仿真获得的凹坑轮廓对比，通过对比可以看出仿真模拟结果与实验测得结果一致，证明了该耦合模型的准确性。

图4 FEM-SPH模型中颗粒角速度与时间的关系Fig.4 Time history of angular velocities of the particles in FEM-SPH model

3.2 冲击速度对颗粒运动行为的影响

研究表明，颗粒的冲击角和方位角是决定颗粒旋向的主要因素，但会受冲击速度的影响发生轻微改变。冲击速度对不同旋向颗粒的运动行为影响程度不同。图6-8展示了前旋旋转(αi=60°θi=20°，αi=50°θi=20°和αi=40°θi=20°)的颗粒在不同冲击速度下产生的运动行为以及反弹角速度的变化情况，由图6～8可知，冲击速度对前旋颗粒的运动行为和旋转方向影响较小，颗粒冲击后的旋转方向不变，旋转角速度变化规律一致，符合前旋颗粒冲蚀磨损速率规律[25]。特别需要说明的是，图6(b)中角速度变化规律表明颗粒接触到延性材料的表面瞬间有后旋趋势，随后转变为前旋旋转，这是特殊工况中后旋向前旋转变的情况，但由于该过程非常短暂，通过实验很难观测到初始的后旋过程，且宏观上颗粒冲击后表现为向前旋转，因此划分为前旋旋转。

图5 实验和仿真预测的case2和case6的凹坑轮廓Fig.5 Experiment and FEM-SPH predicted crater for case 2 and case 6

冲击速度对“后旋”及临界冲击颗粒的运动行为和旋转方向影响影响较大。图9～11展示了“后旋”旋转(αi=60°，θi=50°；αi=60°，θi=50°)和临界冲击(αi=40°，θi=50°)的颗粒在不同冲击速度下产生的运动行为和反弹角速度的变化情况，通过仿真可知，在不同的冲击速度范围内，“后旋”颗粒冲击反弹后的运动行为各不相同，当颗粒入射速度在0～55 m/s时，冲击后运动行为由后旋向前旋转变；当颗粒入射速度在55～80 m/s时，颗粒冲击后出现标准后旋旋转行为；当入射速度大于80 m/s时，颗粒冲击后发生前旋旋转。冲击速度对该种冲击角与方位角组合的临界冲击影响规律与对“后旋”冲击的影响规律近似相同。颗粒冲击后的运动行为和旋转方向与凹坑形成机制有关，具体原因见下文。

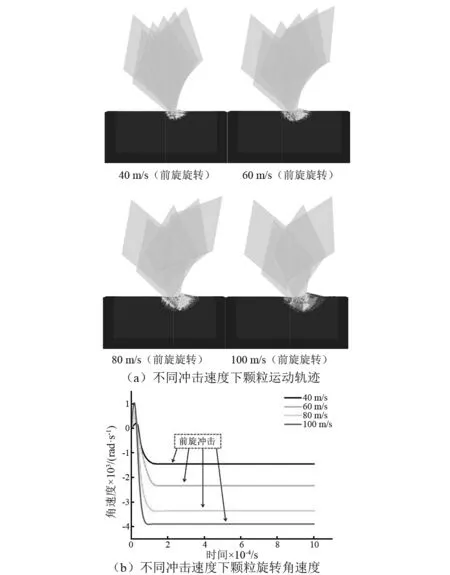
图6 冲击速度对前旋旋转(αi=60°，θi=20°) 颗粒运动行为的影响Fig.6 Effect of impact velocity on kinematicbehavior of particle whenforward rotating(αi=60°，θi=20°)

图7 冲击速度对前旋旋转(αi=50°，θi=20°) 颗粒运动行为的影响Fig.7 Effect of impact velocity on kinematicbehavior of particle whenforward rotating(αi=50°，θi=20°)

图8 冲击速度对前旋旋转(αi=40°，θi=20°) 颗粒运动行为的影响Fig.8 Effect of impact velocity on kinematicbehavior of particle whenforward rotating(αi=40°，θi=20°)

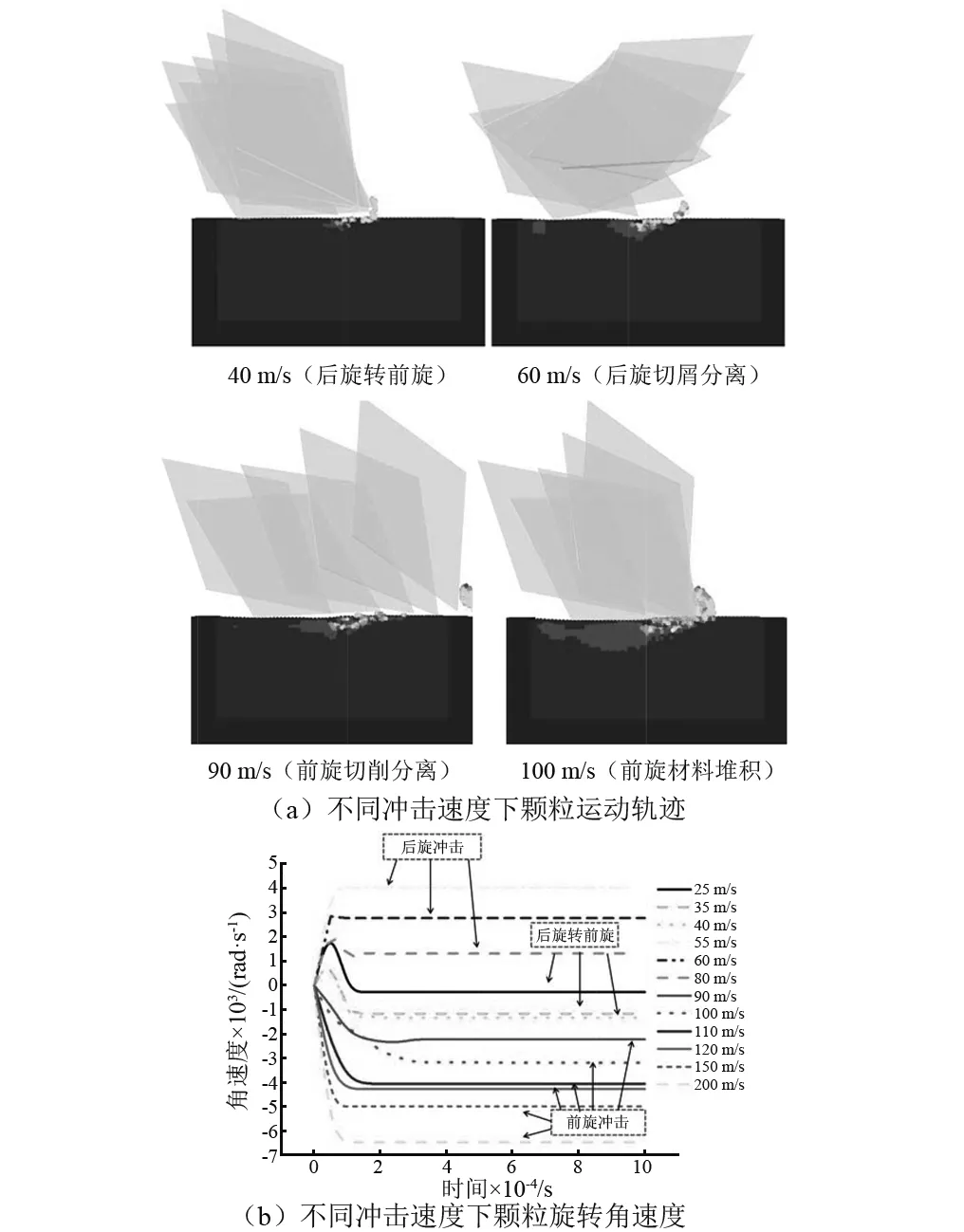
图9 冲击速度对后旋旋转(αi=60°，θi=50°) 颗粒运动行为的影响Fig.9 Effect of impact velocity on kinematicbehavior of particle whenbackward rotating(αi=60°，θi=50°)

图10 冲击速度对后旋(αi=50°，θi=50°) 颗粒运动行为的影响Fig.10 Effect of impact velocity on kinematicbehavior of particle whenbackward rotating(αi=50°，θi=50°)

图11 冲击速度对临界冲击(αi=40°，θi=50°) 颗粒运动行为的影响Fig.11 Effect of impact velocity on kinematicbehavior of particle when critical impact(αi=40°，θi=50°)

3.3 冲击速度对凹坑轮廓的影响

研究表明[25]，前旋旋转的颗粒对延性材料表面产生“犁耕”作用，材料堆积在凹坑表面。本文通过数值模拟对三种不同冲击角与方位角的组合进行研究，获得了冲击速度对前旋冲蚀过程产生的凹坑轮廓形态的影响程度，如图12所示。由图12可知，同一冲击角与方位角的组合下，凹坑的尺寸随着冲击速度的增长成比例增加，但凹坑的轮廓形态基本不变，这表明，随着冲击速度的增加，颗粒尖端对材料产生“犁耕”作用增强，凹坑发生塑性变形的程度更加严重，但冲蚀变形机制未发生改变，表明冲击速度不影响前旋颗粒的冲蚀运动行为。

图12 前旋冲击产生的凹坑轮廓Fig.12 Crater profile generated by forward impact

研究表明，“后旋”旋转的颗粒将导致延性材料“撬起”并切断剔除，但通过仿真可知，在不同的冲击速度范围内，颗粒冲击获得的凹坑轮廓形态各不相同。本文通过两种不同冲击角与方位角的组合，仿真获得了冲击速度对“后旋”冲蚀过程产生凹坑轮廓形态的影响程度，如图13所示。由图13可知，当颗粒的入射速度在0～55 m/s时，颗粒初始动能低，不足以将“撬起”的延性材料切断剔除，未切除的材料对颗粒尖端产生阻碍作用，颗粒运动行为由后旋向前旋转变；当颗粒的入射速度在55～80 m/s时，延性材料表面发生切屑分离，该过程中颗粒会出现标准后旋旋转行为，颗粒尖端将“挖掘撬起”的材料切断剔除，并在材料表面造成一个较浅但较长的凹坑，凹坑轮廓相对比较平滑，深度并不会随冲击速度的增加呈明显增长趋势；当入射速度在80～100 m/s时，延性材料表面发生切屑分离，颗粒尖端仍然能将“挖掘撬起”的材料切断剔除，但冲击后的颗粒发生前旋旋转，这是因为颗粒初始入射速度较大，法向方向嵌入较深，且颗粒尖端嵌入材料的同时不断向前堆挤材料，对延性材料表面产生“挖掘”和“微切削”的综合作用，最终被“挖掘”的材料沿工件表面滑移并切断，切断的材料对颗粒尖端产生阻碍作用，导致颗粒发生前旋旋转；当入射速度大于100 m/s时，颗粒尖端嵌入材料的同时不断向前堆挤材料，对延性材料表面产生“挖掘”和“微切削”的综合作用，但初始速度太大，颗粒法向嵌入太深，颗粒尖端的“挖掘力”小于材料抵抗力，被挖掘的材料无法切断剔除，在“微切削”的作用下产生细长切屑堆积在凹坑前面，导致颗粒发生前旋旋转。

图13 “后旋”冲击产生的凹坑轮廓Fig.13 Crater profile generated by ‘backward’ impact

临界冲击的颗粒理论上无前旋或后旋的旋转趋势，颗粒冲击后应按入射路径返回，但本文研究发现，临界冲击的颗粒运动行为和产生的凹坑轮廓受冲击角与方位角的组合以及冲击速度的影响较大，仿真证明，对于低冲击角和大方位角的临界冲击组合，不同冲击速度下颗粒运动行为和凹坑轮廓与“后旋”冲击产生的规律一致，如图14所示；对于高冲击角和小方位角的临界冲击组合，不同冲击速度下颗粒运动行为和凹坑轮廓与前旋冲击产生的规律一致。由前人的研究成果可知，临界冲击下颗粒的动能损失最为严重，颗粒旋转行为被大大抑制，但仍会对接近临界冲击的其它冲击角与方位角的组合存在记忆功能，因此会出现前旋或后旋的冲击行为。

图14 临界冲击(αi=40°,θi=50°)产生的凹坑轮廓Fig.14 Crater profile generated by critical impact (αi=40°,θi=50°)

颗粒多次冲击现象是冲蚀磨损过程中一个特殊的现象，颗粒前旋旋转和后旋旋转皆会产生多次冲击，由前期的研究成果可知，在非垂直冲击和负方位角组合下，前旋颗粒会出现二次乃至三次冲击，且方位角绝对值越大，颗粒出现的冲击次数越多；对于颗粒后旋产生切屑分离的工况而言，在非垂直冲击和正方位角组合下，颗粒至多出现二次冲击，且方位角越大，二次冲击效果越明显，如图13所示。

4 结 论

(1) 针对菱形颗粒的冲蚀磨损过程建立了基于拉格朗日法的FEM-SPH耦合数值计算模型，通过该模型重现其他研究学者的冲击实验，最终实验测量结果与仿真预测结果吻合度较高，颗粒运动轨迹及反弹参数高度一致，验证了该耦合模型的准确性。

(2) 冲击角和方位角是决定颗粒旋转的关键因素，但会受冲击速度的影响发生变化。冲击速度对前旋颗粒运动参数的量值影响较大，但对冲击诱导的颗粒旋转行为影响较小，不同冲击速度下导致的凹坑轮廓形状基本不变，“犁耕”的材料堆积在凹坑表面，符合前旋颗粒冲蚀磨损规律。

(3) 冲击速度对“后旋”旋转的颗粒影响较大，当vi在55～100 m/s范围内时，延性材料表面发生切屑分离，颗粒出现标准后旋旋转，当vi小于或大于该范围，只发生材料堆积，均无切屑分离现象发生，低速冲击产生的材料堆积是由于颗粒初始动能不足无法将“挖掘”的材料切断剔除，高速冲击产生的材料堆积是由于颗粒法向嵌入太深，颗粒尖端的“挖掘力”小于材料抵抗力，被挖掘的材料无法切断剔除。

(4) 临界冲击下颗粒的动能损失最为严重，颗粒旋转行为被大大抑制，但仍会对接近临界冲击的其它冲击角与方位角的组合存在记忆功能，因此会出现前旋或后旋的冲击行为。