弹性高超声速飞行器输入饱和抑制backstepping控制

路 遥 ， 孙 友， 路坤锋

(北京航天自动控制研究所，北京 100854)

高超声速飞行器是指飞行马赫数大于5的飞行器[1]。它具有机动灵活、隐身性高、突防能力强等特点，可以作为战略突袭武器的发射平台，因而受到了各个航天强国的广泛关注。其中，乘波体构形的吸气式高超声速飞行器(Air-breathing Hypersonic Vehicle, AHV)因具有较高的升阻比，被认为是高超声速飞行器最好的气动外形[2]，具有广阔的应用前景。

飞行控制系统是高超声速飞行器实现安全飞行的关键因素。高超声速飞行器模型普遍具有高度非线性、参数不确定的特点，为其设计控制器已是不易；而AHV动力学模型中存在非最小相位特性，且AHV通常采用轻质材料的细长体设计，因此其弹性振动效应较为显著，这些特点使得为AHV设计控制器更加困难。

在设计AHV的总体几何构型时，通常控制俯仰通道姿态的执行机构只安装升降舵[3]；然而，AHV的升降舵对升力的影响较一般飞行器更为显著，使得飞行器纵向通道的轨迹控制与姿态控制之前存在强烈的耦合，这给飞行器控制系统的设计造成很大困难。针对这一问题，目前研究者通常采用增加鸭翼的方式予以解决[4-6]。但是，增加额外的控制舵面会为飞行器带来一些不利的影响。文献[7]指出，增加鸭翼会影响高超声速飞行器热量保护系统的设计，而且鸭式布局还会降低飞行器的隐身性能。因此，是否可以在AHV仅安装升降舵的情况下，同时考虑机体弹性模态的影响，为其设计纵向通道的控制器，是一个值得研究的问题。在目前的研究中，文献[8]考虑了机体的弹性模态，证明了所提出的控制器不会引起弹性模态发散；但其控制器中并未对弹性模态影响进行补偿，因此其闭环系统的动态特性较差，在控制的初始阶段存在明显的震荡。文献[9]将弹性模态项视为一类系统干扰项，并设计干扰观测器对其进行估计，在控制器设计中予以补偿，取得了良好的控制效果；其对机体中弹性模态的处理方式值得借鉴，但其仍采用增加鸭翼舵的方式抵消升降舵对升力的影响。文献[10]与文献[9]类似，同样将弹性模态项视为干扰项，并进一步考虑了控制输入量的限制，但在控制器设计过程中未考虑对控制量进行抑制，因此仍存在控制量达到饱和的现象。文献[11]也将弹性模态项视为系统的干扰项，但其弹性模态干扰项建模中存在控制量升降舵偏角，这影响其设计的干扰观测器的观测精度，进而影响非线性控制器的控制精度。文献[12]以无鸭翼AHV为研究对象，将机体的弹性模态视为干扰项，利用神经网络对其动态进行逼近，设计了预设性能非线性控制器，取得了一定的控制效果；然而文中在进行控制器设计时基于升降舵偏转角对升力的影响可忽略的假设，导致飞行器在小攻角飞行时控制精度不高。

本文研究弹性AHV纵向通道姿态跟踪控制问题，针对其中存在的弹性模态扰动影响、控制量易到达饱和的问题，在飞行器仅安装升降舵的情况下，基于backstepping方法设计非线性控制器。将飞行器的弹性模态视为系统的不确定干扰项，设计干扰观测器对其进行估计，并在控制器中进行补偿。引入非线性增益函数，采用动态的非线性增益函数代替传统的固定增益策略，提高控制执行机构的饱和抑制能力。

1 问题描述

本文以文献[12]中AHV纵向通道姿态动力学模型作为研究对象，可描述为：

(1)

(2)

(3)

(4)

式中：α,Q分别表示飞行器的攻角和俯仰角速度；V,γ,m,Iyy,g分别表示飞行器的速度、航迹角、质量、俯仰方向转动惯量和重力加速度；T,L,M分别表示发动机推力、升力和俯仰力矩；ηi,i=1,2表示第i阶弹性模态；ψi表示耦合系数，ki=1+ψi/Iyy；ξi,ωi分别表示弹性模态ηi的阻尼系数和自然频率；Ni表示广义力。L、M和Ni可近似描述成如下形式：

(5)

(6)

(7)

(8)

(9)

(10)

控制器的设计目标为使飞行器的攻角跟踪给定的参考指令αref，同时闭环系统中的所有信号有界稳定。本文在设计控制器时基于以下合理假设：

假设1[12]αref信号及其一阶微分已知且连续有界。

假设2[3]式(1)中Tsinα远小于L，可忽略不计。

2 Backstepping控制器设计

2.1 基于Backstepping的非线性控制器设计

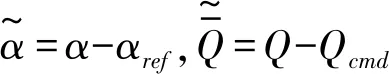
(11)

(12)

式中，

(13)

(14)

g2=

(15)

(16)

式中：Δ为弹性模态项。已有研究表明，当弹性模态ηi的阻尼系数满足0<ξi<1，自然频率满足ωi>0，且攻角有界时，ηi的动态过程是渐近稳定的[3,13]；因此，可以将Δ视为干扰项，通过设计干扰观测器对其进行估计，在backstepping控制器中进行补偿。

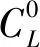
注2 与文献[12]中的弹性干扰项相比，式(16)中的干扰项Δ中不包含控制量δe的相关项，这有利于对Δ进行精确估计。若Δ中含有δe的相关项，则Δ的实际值只有在δe确定后才能确定；而δe的设计又依赖于对Δ的估计，这意味着对Δ进行估计的工作需要在δe确定前完成；这种情况下容易导致Δ的估计值与实际值之间出现较大的偏差。

由于式(11)和式(12)中均包含控制量δe，因此传统的适用于严格反馈控制系统的backstepping方法不再适用。为此，令

u=Q+g1δe

(17)

此时式(11)可改写为

(18)

以u为虚拟控制量，设计如下控制律

(19)

式中:k3>0为控制增益。由式(17)可知，ucmd由Qcmd和g1δe两部分组成，即：

ucmd=Qcmd+g1δe

(20)

而δe在组成ucmd的同时也需要控制状态Q趋近于虚拟控制量Qcmd。基于式(12)，若Qcmd已确定，设计如下控制律：

(21)

(22)

式中:ς为滤波器系数，通常取0.01≤ς≤0.05，Δt为控制周期。由文献[14]中定理1的证明过程可知在假设1的条件下，∃B1,B2>0使得下式满足：

(23)

(24)

这样，通过联立式(20)、式(22)和式(24)组成方程组，即可得到δe的实际值。

2.2 基于干扰观测器的弹性模态扰动项补偿策略

引理1[15]对于如下系统：

(25)

式中:z1∈R,z2∈R若式(25)的解满足z1(t)→0,z2(t)→0(t→∞)，则对于任意有界可积输入信号v(t)和R>0，下式

(26)

以下基于引理1设计非线性干扰观测器。首先给出以下定理：

定理1 对于如下系统：

(27)

其中R>0，ϑ(x)的形式如下：

(28)

当常数a>0时，系统(27)的解满足z1(t)→0,z2(t)→0(t→∞)。

(29)

由LaSalle不变性原理[16]可知系统式(27)的解满足z1(t)→0,z2(t)→0 (t→∞)。

证毕.

在定理1的基础上可设计如下形式的干扰观测器：

(30)

2.3 基于非线性增益函数的执行机构饱和抑制策略

针对机体弹性模态(干扰项补偿误差)可能引起的控制量超出限制的问题，本节对式(19)和式(24)中的误差项进行进一步优化处理，设计动态的非线性增益函数代替传统的固定增益策略。非线性增益函数设计如下：

(31)

式中:sgn(·)表示符号函数，b>0为调节参数，μ>0为误差阈值项。取μ=0.1，当b=2和b=4时，G(x,b,μ)的曲线如图1所示。

图1 时曲线图Fig.1 The curve ofwhen

由函数形式易知G(x,b,μ)连续可导，表达式为：

(32)

且G(x,b,μ)对于x严格单调递增。定义

(33)

由G(x,b,μ)的单调性和式(32)易知H(x,b,μ)也对于x单调递增。引入非线性增益策略，将式(19)和式(24)的控制律更新为：

(34)

(35)

式中ζ为鲁棒项，表达式为：

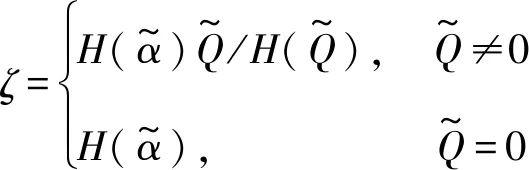
(36)

注意到当|x|>μ时|G(x,b,μ)|<|x|且0μ。由此可知，若x表示闭环系统的跟踪误差，当其幅值在阈值μ之内时，非线性增益策略的作用与传统的固定增益策略相同；但当闭环系统因扰动出现较大的跟踪误差时，非线性增益策略能够对控制量起到一定的抑制作用，防止其达到饱和。调节参数b和阈值μ可根据实际被控对象的气动特性以及控制执行机构的控制能力进行设置。

3 稳定性分析

(37)

对其求导得：

(38)

(39)

(40)

4 仿真分析

图2 攻角跟踪结果Fig.2 Tacking result of angle of attack

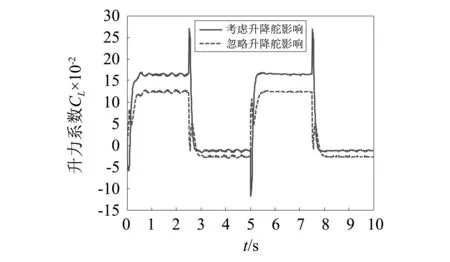
图3 升力系数CL比较曲线Fig.3 Comparative curve of lift coefficient CL

图4 干扰观测器估计结果Fig.4 Estimated results of disturbance observer

接下来验证2.3节提出的非线性增益函数的执行机构饱和抑制策略的效果。为对比本文方法的控制效果，同时采用不含非线性增益函数执行机构饱和抑制策略的方法(即式(19)和式(24)所示的控制律)进行仿真，对比仿真结果如图5～图6所示。

图5 升降舵偏角比较结果Fig.5 Comparative result of the elevator deflection angle

图6 俯仰角速度误差曲线Fig.6 Curves of the error of pitch angle angular

图5为两种策略下控制量升降舵偏角的比较结果，结合图2和式(9)可知，图2中考虑升降舵影响与不考虑升降舵影响的差异的大小与图5中升降舵偏角的实际大小和正负号在数量上是对应的，这进一步佐证了注1中提到的“δe对升力的影响是不能忽略的”。图6为本文算法下俯仰角速度误差曲线。可以看出，当俯仰角速度误差较大时，本文算法提出的基于非线性增益函数的执行机构饱和抑制策略能够有效抑制控制量的大小，防止其达到饱和状态；而不含有饱和抑制策略的控制方法将出现控制量饱和的问题。这是由于非线性增益函数参数设置中μ2取值的意义为当俯仰角速度误差超过2.5时，执行机构饱和抑制策略开始起作用，通过降低控制器增益降低控制量的大小，进而达到防止控制量出现饱和情况的目的。

图7为状态量俯仰角速度的仿真结果曲线，可以看出该状态量是稳定的。

图7 俯仰角速度曲线Fig.7 Curves of pitch angular velocity

5 结 论

(2) 在弹性模态扰动项的建模中剥离了控制量相关项，并设计了非线性干扰观测器对扰动项进行估计，在控制器中予以补偿，提高了控制器的控制性能。

(3) 引入非线性增益函数代替传统的固定增益策略，提高了系统控制输入量的饱和抑制能力。

(4) 在飞行器俯仰通道控制执行机构只有升降舵的情况下，不能忽略升降舵偏转对升力的影响。