基于光纤Bragg光栅传感的轴向柱塞泵非介入式振动测量方法

何祯鑫， 张正义， 李洪才， 刘春桐， 冯永保

(1.火箭军工程大学 导弹工程学院，西安 710025；2.高新技术研究所，山东 青州 262500)

非介入式检测技术是目前的研究热点之一，国内外科研单位对其开展了长期深入的研究[1]。在液压设备的非介入检测方面，振动信号测量是经常被采用的方法之一，但传统电磁类振动传感器不能适应强电磁干扰、温湿度等复杂特殊环境下的测量要求。与传统传感方式相比，光纤传感器具有以下优点：①由于光纤传感是通过光波长的变化敏感外界物理量作用的，因此光纤传感器的灵敏度和线性度好；②因光纤传感器利用光波传输信息，而光纤又是电绝缘、耐腐蚀的传输媒介，使其具有抗电磁干扰、抗腐蚀、耐高压高温、防爆、本质安全、稳定性好等特点，能在恶劣环境下进行非接触式、非介入式、非破坏性以及远距离测量，可以方便有效地用于强电磁干扰、易燃易爆、核辐射区等场合；③由于被测信号以光波为载体，信息容量大，同一光纤可传输多路信号，且便于与计算机相连，易实现智能化、分布式、远距离监控。④可以对多个参量进行测量，如温度、压力、振动、流量、浓度等，满足多样需求。基于光纤传感器具有的上述优点，已经被广泛应用于石油化工、电力系统、医学、结构动力学等多个特殊要求的领域，近年来也逐渐成为状态监测及故障诊断的新型传感技术之一[2-4]。

Berkoff等[5]研制了一种基于嵌入式结构的加速度传感器，将FBG嵌入到位于质量块与刚性基座间的橡胶材料中。振动时，质量块将使弹性体出现横向变形，产生FBG应变，引起中心波长的改变，但易被横向振动干扰，导致横向交叉灵敏度较大。Basumallick等[6]先将普通悬臂梁表面添加一层聚酰亚胺层，然后把光纤光栅粘贴在聚酰亚胺层，在其固有频率未减小的前提下，将其灵敏度增加了一倍。Karabacak等[7]设计了一种FBG振动高速监测系统，能够在多种恶劣环境下实现振动测量。张东生等[8]设计了一种基于钢管的FBG加速度传感器，能够测量高频信号。张晓蕾等[9]研制了一种紧凑的硅凝胶材料的双半圆型FBG振动传感器，该传感器有着良好的线性度，同时环境温度与横向交叉灵敏度的影响能够被较好地避免。徐胜明等[10]研制了一种石油管道安全监测的振动传感器，能够对管道上的各种信号进行有效区分。通过查阅相关文献，目前尚未发现利用光纤传感技术对液压泵进行非介入式振动测量，为液压系统故障诊断提供数据支撑。

因此本文在分析光纤光栅振动传感原理的基础上，充分利用光纤光栅传感独特的技术优势，并结合振动频率高精度、抗干扰检测的实际需要，相比较普通悬臂梁，双等强度悬臂梁具有频带范围更宽，加速度灵敏度更高，设计的传感器横向抗干扰能力更强的优点，研制了一种双等强度悬臂梁式光纤光栅振动传感器；对斜盘式轴向柱塞泵模态分析，优化传感器布点，利用设计的FBG传感器对斜盘式轴向柱塞泵振动测量，通过仿真与试验验证了振动传感器的测量精度和可靠性，对于液压系统状态监测与故障诊断具有重要意义。

1 FBG振动传感模型

由光纤光栅耦合模理论，布拉格方程可表示为

λB=2neffΛ

(1)

式中：λB为FBG中心波长，neff为有效折射率，Λ表示光栅周期。可知，光栅周期Λ以及有效折射率neff的数值会受到FBG所处外界环境的影响，导致中心波长λB产生漂移。在FBG受到应力时，会被压缩或拉伸，然后使光栅周期Λ发生变化；同样，根据光纤弹光效应，FBG有效折射率neff受到应力时也会改变[11]。

对式(1)进行微分后，FBG中心波长漂移可认为是由应力引成的

ΔλB=2neffΔΛ+2ΔneffΛ

(2)

式中：ΔλB为中心波长变化量，Δneff表示FBG处于应力作用时的有效折射率变化量，ΔΛ表示FBG由于应力作用导致的弹性变形量。通常在传感系统中利用FBG对轴向上应变的感应特性完成传感检测。

温度恒定情况下，FBG只受到轴向应力作用，进一步可以得到

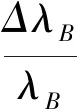
(3)

式中：ε为外界振动信号作用下光纤光栅的动态应变，Pε为有效弹光系数，Kε为应变灵敏度系数。在一根FBG中，有效弹光系数是常数，在周围环境温度保持不变的时候，Kε也是常数，表明FBG中心波长的偏移量和轴向应变的线性度很好。

在光纤光栅振动传感器受到外界振动信号时，传感器可以把实测振动参量转变为光栅轴向的动态应变量，即光纤光栅反射谱会出现和振动信号频率相同的周期性变化漂移。因此，只要能够检测到光纤光栅中心波长的周期性漂移情况，就能够实现振动信号传感。

在忽略应变与温度交叉敏感的前提下，根据式(3)可以得到，波长漂移量可表示成

ΔλB=λB(1-Pe)ε

(4)

由式(4)可得，波长变化量ΔλB和轴向应变ε属于线性关系，先测中心波长变化规律，通过振动传感器响应函数，完成振动信号传感。也就是说，在振动传感的过程中，采集光纤光栅中心波长变化数据，经过傅里叶变换后，所反映的振动频率值即为待测频率值。

2 双等强度悬臂梁式FBG振动传感器设计

2.1 FBG振动传感器的设计原理

在传统单悬臂梁式的基础上，本传感器的设计采取双等强度悬臂梁式结构，等效截面厚度等于同样尺寸单等强度悬臂梁的2倍，提高固有频率的同时，拓宽了工作频带，传感器采集的振动信号更为丰富。

当力F作用在等强度悬臂梁顶端的时候，位于悬臂梁上下两表面的轴向应变ε均匀分布，可表示为

(5)

悬臂梁的等效弹簧刚度k为

(6)

式中：L表示梁的长度，h为梁的厚度，E表示梁的杨氏模量，B为梁的宽度。

悬臂梁式传感器的固有角频率可表示为

(7)

式中：m表示悬臂梁传感器的等效惯性质量。

FBG中心波长变化量和振动加速度关系可表示为

(8)

因此，FBG振动传感器灵敏度可表示为

(9)

2.2 FBG振动传感器的设计

(1)传感器关键指标要求

为了使光纤光栅振动传感器更好地测量轴向柱塞振动频率，并结合柱塞泵工况，设计的传感器关键指标要求如下：

① 测量精度≤3%；

② 灵敏度≥0.01 nm/(m·s-2)；

③ 线性度≥99%；

④ 测量范围为[10～230]Hz；

⑤ 环境温度为[20～70]℃。

另外，要求设计的传感器具有良好的频率响应特性以及横向抗干扰等性能等。

(2)传感器基本结构

双等强度悬臂梁基本的结构设计如图1所示，采取了对称结构，悬臂梁的一端固联质量块，另一端与振动体固定。使用AB胶把FBG粘贴至悬臂梁表面，将FBG严格粘贴放置于悬臂梁表面的中轴线上。

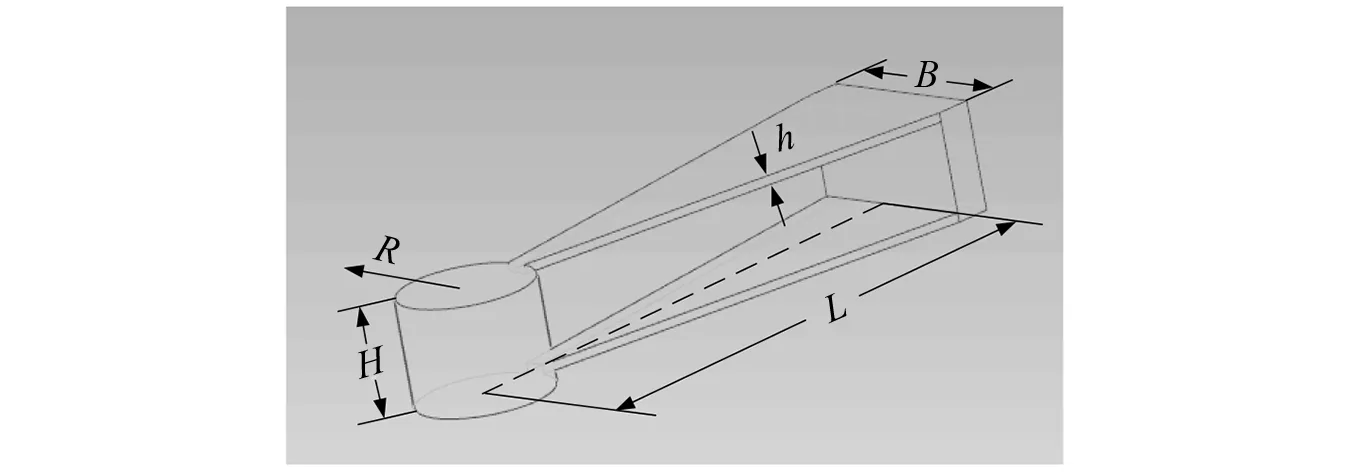
图1 传感器结构示意图Fig.1 Schematic diagram of sensor structure.

通过对比几种常见材料的性能属性及加工难易程度，传感器的材质选用304#不锈钢。

斜轴式轴向柱塞泵振动频率f同泵的柱塞数Z以及转速n有直接关系，函数关系为

(10)

在额定转速1 200 r/min下运转的泵振动频率为140 Hz。因此，将所设计的振动传感器的固有频率大约设置为185 Hz，由此设计该振动传感器的结构尺寸，具体结构参数，如表1所示。

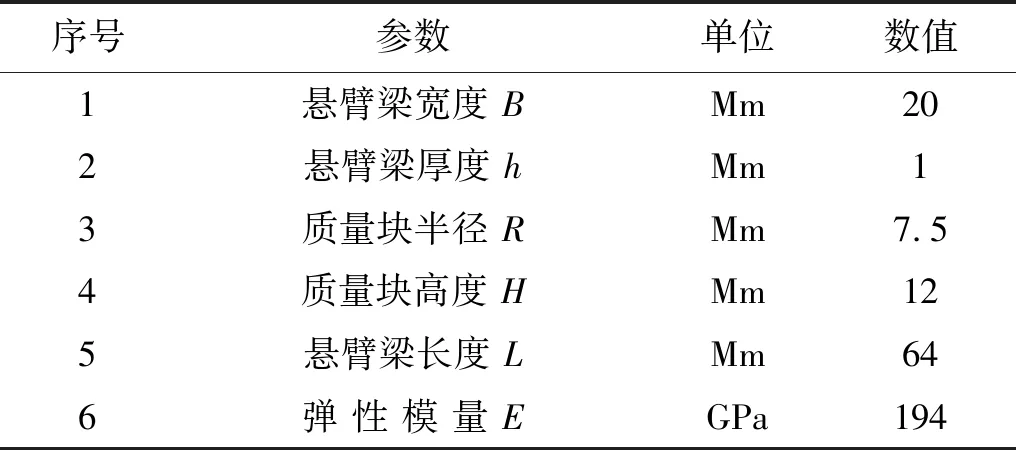
表1 传感器结构参数Tab.1 Structure parameters of the sensor

(3)FBG振动传感器性能仿真

利用有限元分析方法对设计的双等强度悬臂梁式FBG振动传感器进行仿真分析，验证其理论参数的准确性和加速度力学模型的可靠性。固有频率为振动传感器重要参数之一[12]。根据式(7)可得，悬臂梁结构固有频率与其刚度和等效惯性质量是紧密联系的。

建立双等强度悬臂梁式FBG振动传感器仿真模型，将固定约束施加于悬臂梁的底座，并将一个1 N的力添加于悬臂梁自由端的z轴正向上，分析处理得到悬臂梁的自由端的位移是0.040 895 mm，如图2，3所示。

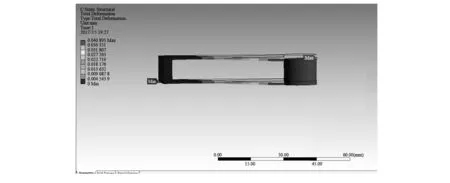
图2 悬臂梁自由端z轴纵向位移Fig.2 Longitudinal displacement of cantilever beam free end z-axis

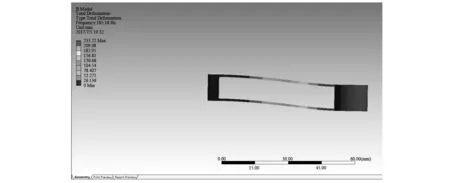
图3 悬臂梁的固有频率仿真Fig.3 Natural frequency simulation of cantilever beam

通过式(6)能够得到，该悬臂梁结构刚度的理论计算结果是25.431 31×103N/m，仿真分析结果是24.452 87×103N/m，误差仅为4.0%，验证了传感器模型具有可靠性。

在传感器的底座添加一个固定约束，通过模态分析得到悬臂梁结构固有频率是185.18 Hz。通常将悬臂梁传感器的等效惯性质量替代为其自由端的质量块的质量，然而得出的固有频率值与仿真结果差别较大。因此，当悬臂梁传感器质量块较轻且尺寸较小时，就必须考虑梁的质量，根据机械振动原理[13]，等强度悬臂梁等效惯性质量是

m=mK+0.24mL

(11)

式中：mK为质量块质量，mL为悬臂梁质量。根据式(7)能够得到，所设计的悬臂梁振动传感器固有频率是183.97 Hz，同仿真结果之间的误差是0.66%。

由于传感器的自重，再加上基座、质量块和悬臂梁连接等一系列实际情况的存在，梁上产生的应变也并非全都一致。一般将光栅固定在梁中轴线位置，以确保FBG受到的应变尽可能大，同时做到均匀变化，避免FBG反射谱产生啁啾现象，影响系统的解调性能。

通过有限元软件中静力学分析模块，添加一个固定约束于悬臂梁传感器的基座位置，然后添加1 N的力于z轴的正方向上，同时在梁中轴线位置处建立分析路径，再添加其各位置的应变计算，得到如图4所示的分析结果。

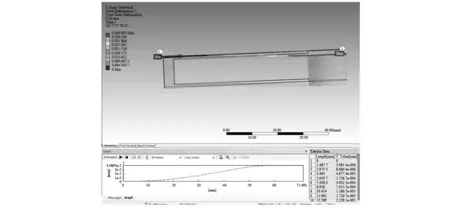
图4 自由端1 N载荷下等强度梁中轴线上应变分布情况Fig.4 The strain distribution on the central axis of the beam with 1 N load of free end

图4中，1位置表示悬臂梁固定端的端点，2位置表示悬臂梁自由端的端点。根据图中下方曲线的分析路径方向上的应变曲线，说明该悬臂梁在35～45 mm位置的应变比较大，同时均匀变化，所以应将光栅固定在该区域内，以此来确保传感器达到最佳的性能。

3 轴向柱塞泵模态分析与采样点位优化

3.1 模型建立与模态分析

按照轴向柱塞泵实际结构和参数，构建斜轴式轴向柱塞泵壳体立体简化模型，导入至仿真软件几何分析模块中，将简化模型给予网格划分处理，选取四面体网格划分方式，建立轴向柱塞泵有限元分析模型。

泵的安装采取与电机以及钟形罩相互连接固定的方式，所以把固支约束设置在泵壳的前端(即右端面)，对泵体模型进行模态分析。泵前4阶模态固有频率分别为162.41 Hz，212.73 Hz，545.67 Hz，589.74 Hz。根据振动模态的有关理论，结构振动中低阶模态发挥着重要作用，文中仅分析前4阶模态，结果如图5所示。

由此可见，泵体振动较剧烈区域为柱塞泵左侧泵体；泵体总体振动呈现对称分布，这与柱塞泵结构的对称性一致；泵壳的前端(即右端面)振动最小。

3.2 采样点位的优化选择

轴向柱塞泵的活塞通常在泵体的轴向上往复运动，仿真得出轴向柱塞泵左侧泵体的振动最强烈。在柱塞泵出现异常故障时，振动频率发生变化，左侧泵体位置更有利于对异常故障的敏感，能更好地进行故障诊断，因此把设计的FBG振动传感器固定在柱塞泵左侧泵体侧面中心位置处以及左侧泵体端面边缘处。

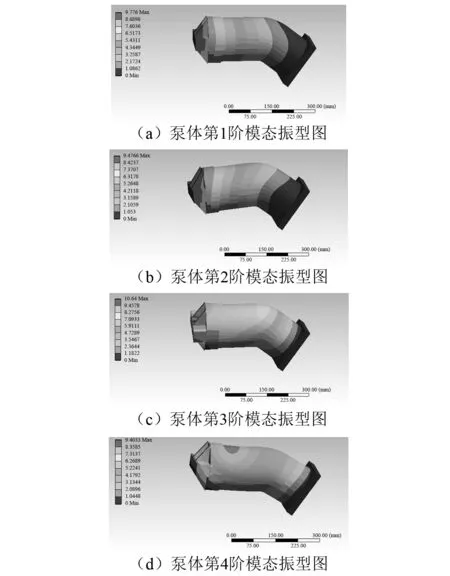
图5 泵体前4阶模态振型图Fig.5 The first 4-step vibration mode of pump body

4 振动频率试验与分析

4.1 传感解调系统

传感解调系统结构示意如图6所示，一定波段的光由宽带光源射出，而后光波进入光纤光栅振动传感器，携带被测振动信号的反射光进入可调谐F-P滤波器解调模块，从而得到振动传感器中心波长的偏移信号。解调模块经USB接口总线把解调信号传递到上位机，经过上位机数据分析与处理，得到系统待测物理量数值大小。

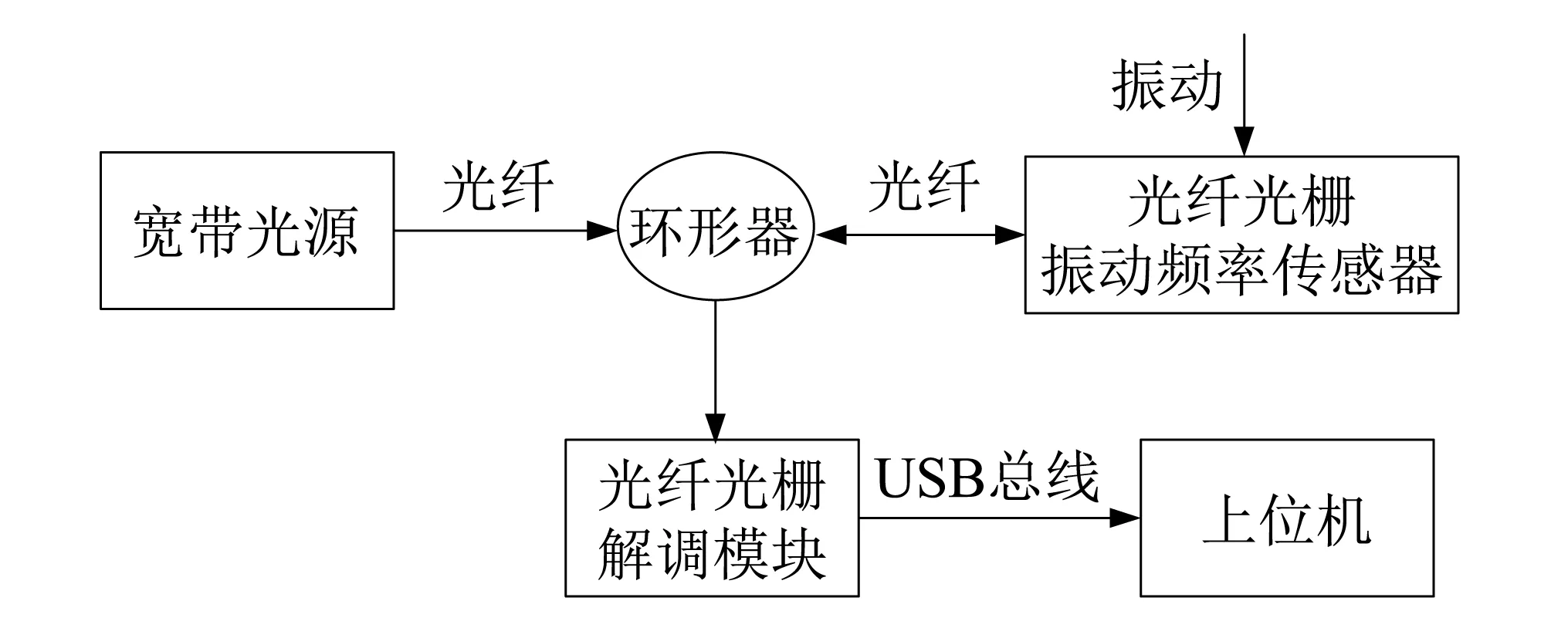
图6 传感解调系统Fig.6 Sensor demodulation system

为更好地实现系统解调要求，F-P腔的选择必须考虑解调精度和解调范围。由于可调谐F-P滤波器性能的设计要求，应该采用BaySpec 公司生产的WaveCapture 系列的高速光纤光栅解调模块。解调系统中的光源选择SLD光源，体积小，可靠性好，同时光功率较高，且带宽较大。解调仪的分辨率达到1 pm。

4.2 振动台试验与分析

振动传感器的灵敏度和固有频率是振动传感器的关键参数，为此主要进行传感器频率测量精度、灵敏度特性分析、线性度分析和频率响应特性分析。

(1)振动台振动频率测试实验

将设计的光纤光栅振动传感器固定于振动台表面，同时保证梁表面和振动方向为相互垂直关系，将传感器连接头连接至解调设备，如图7所示。

图7 振动台振动频率测试实验Fig.7 Vibration frequency experiment using vibration table

调节振动台的输出频率由10 Hz一直增加至230 Hz，并步长为20 Hz，读取对应的FBG振动频率传感器测量的频率值，如表2所示，fZ表示振动台频率值，fG表示FBG振动频率传感器测量频率值。

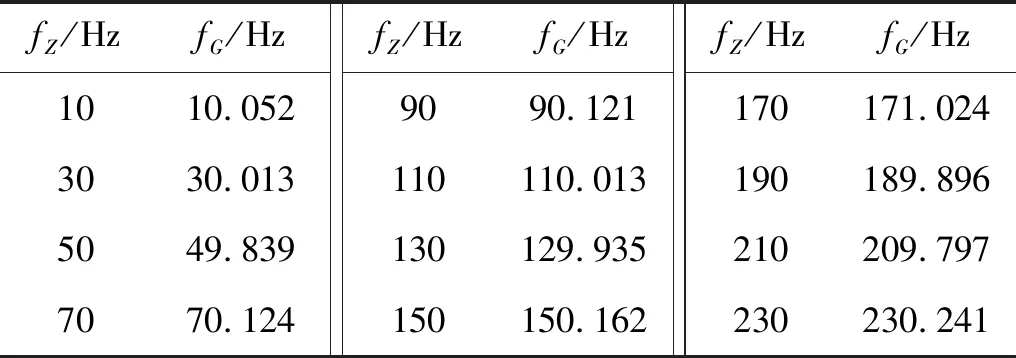
表2 振动台振动频率测量数据Tab.2 Vibration frequency data using vibration table

由此可见，双等强度悬臂梁式FBG振动传感器的振动测量平均误差约为0.21%，其中在传感器最佳测量频率段的平均误差达到0.031%，结果与振动台设置频率较好吻合，说明传感器具有较高精度，能够达到高精度测量振动频率的要求。

(2)灵敏度特性分析实验

调节振动台的输出频率保持15 Hz，并利用加速度传感器ADIS 16405均匀地调节振动台的振动加速度值由1.0 m/s2增加至10.0 m/s2，步长大约为1.0 m/s2；使用解调设备监测记录各振动加速度对应的FBG振动传感器的波长输出信号，得到在振动频率恒定下，不同振动加速度对应的振动传感器FBG中心波长的漂移量，即得出振动加速度和FBG中心波长的漂移量间的变化规律，对实验数据进行拟合，获得FBG振动传感器在15 Hz振动频率时的灵敏度特性，如图8所示。

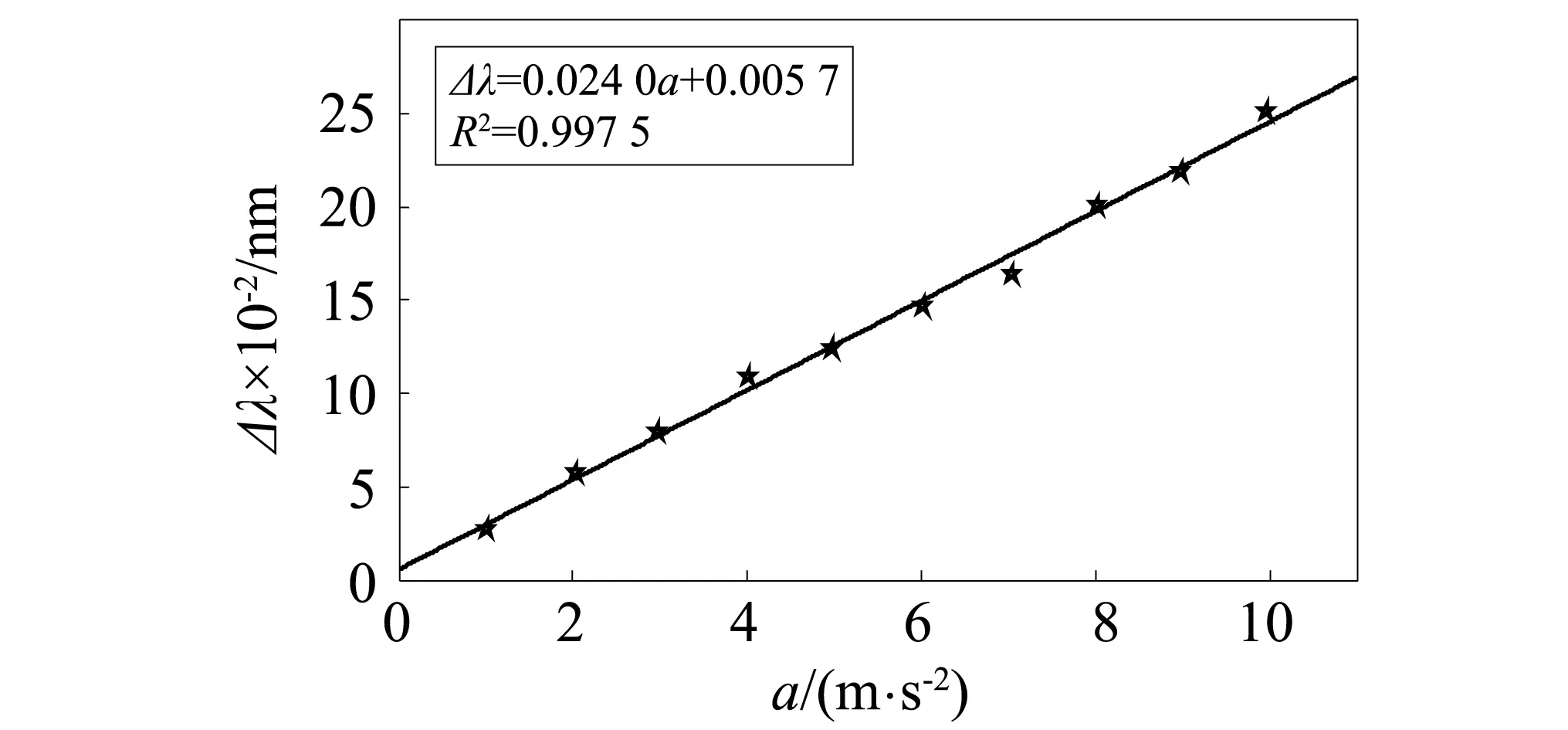
图8 15 Hz对应的传感器灵敏度线性拟合曲线Fig.8 Linear fitting curve of sensor sensitivity under 15 Hz

由式(8)可得，FBG中心波长变化量和加速度存在线性关系，与测量数据结果吻合。通过最小二乘法线性拟合测量数据，得出FBG中心波长的偏移量Δλ与加速度a的函数关系是

Δλ=0.024 0a+0.005 7

(12)

该拟合结果的线性拟合度是0.997 5，说明该振动传感器灵敏度是0.024 0 nm/(m·s-2)，同时数据拟合度较好，所研制的FBG振动传感器有着良好的灵敏度。

(3)线性度分析实验

相同方法和步骤，加速度信号频率分别为25 Hz、35 Hz情况下，测量传感器在加速度大小由1.0 m/s2、以大约1.0 m/s2的步长增加至10.0 m/s2时对应的中心波长漂移量，对波长数据拟合得到图9和图10。

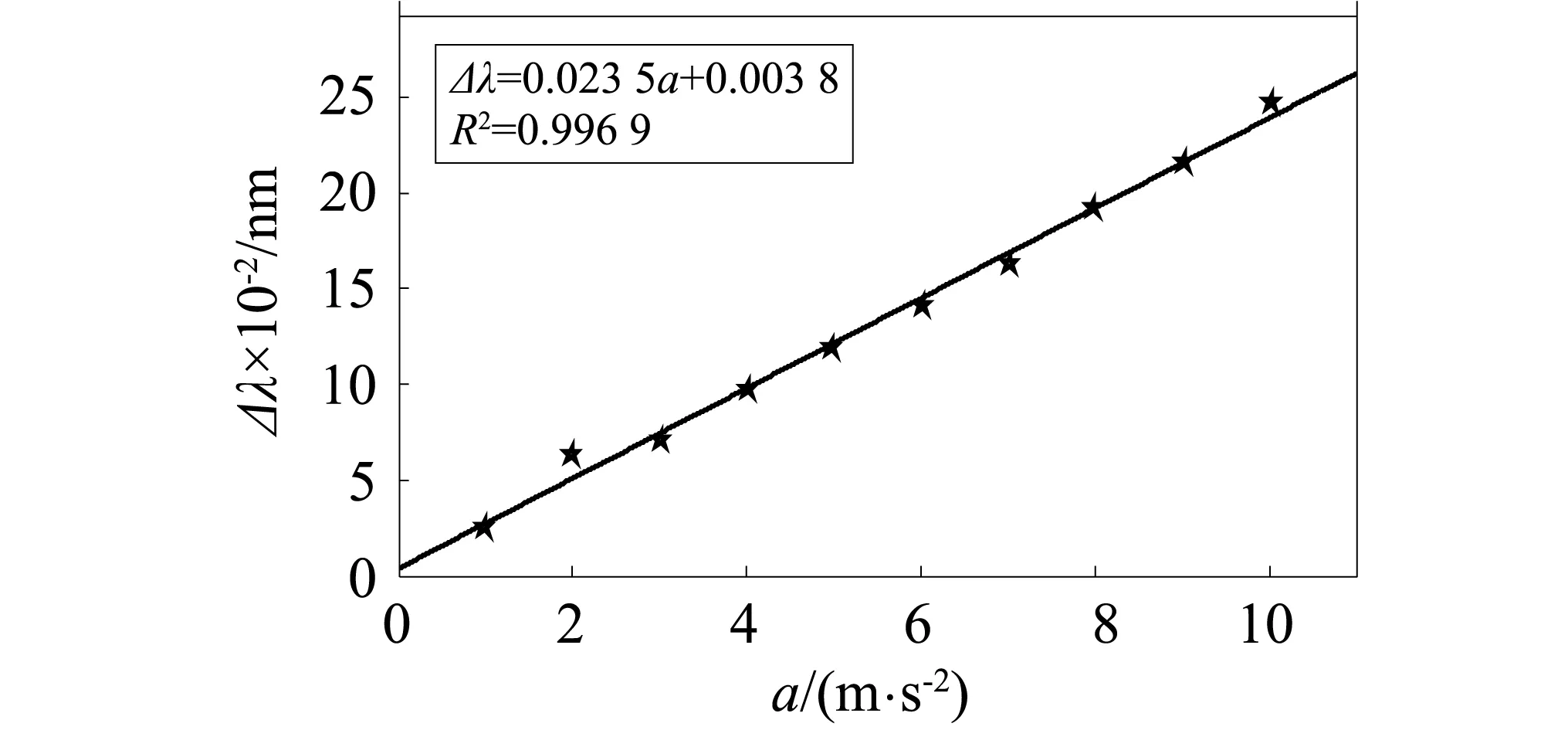
图9 25 Hz对应的传感器灵敏度线性拟合曲线Fig.9 Linear fitting curve of sensor sensitivity under 25 Hz

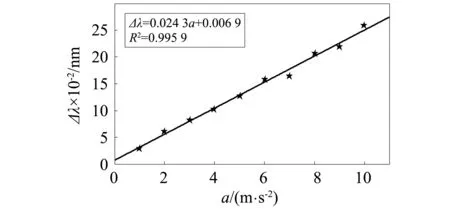
图10 35 Hz对应的传感器灵敏度线性拟合曲线Fig.10 Linear fitting curve of sensor sensitivity under 35 Hz

由上可得，频率为15 Hz、25 Hz和35 Hz时，传感器灵敏度分别是0.024 0 nm/(m·s-2)、0.023 5 nm/(m·s-2)和0.024 3 nm/(m·s-2)，且其线性拟合度分别是0.997 5、0.996 9和0.995 9，灵敏度平均值是0.024 0 nm/(m·s-2)，灵敏度误差在2%左右，表明此传感器的线性度较好。

(4)频率响应特性分析实验

将振动台振动加速度设置成5 m/s2，且控制振动台输出频率以20 Hz步长由5 Hz均匀增加至305 Hz。同时为进一步精确地测量传感器固有频率，在185 Hz位置附近，选取多个频率点进行测量，得出不同频率下的FBG中心波长漂移量，对测量数据拟合曲线如图11所示。

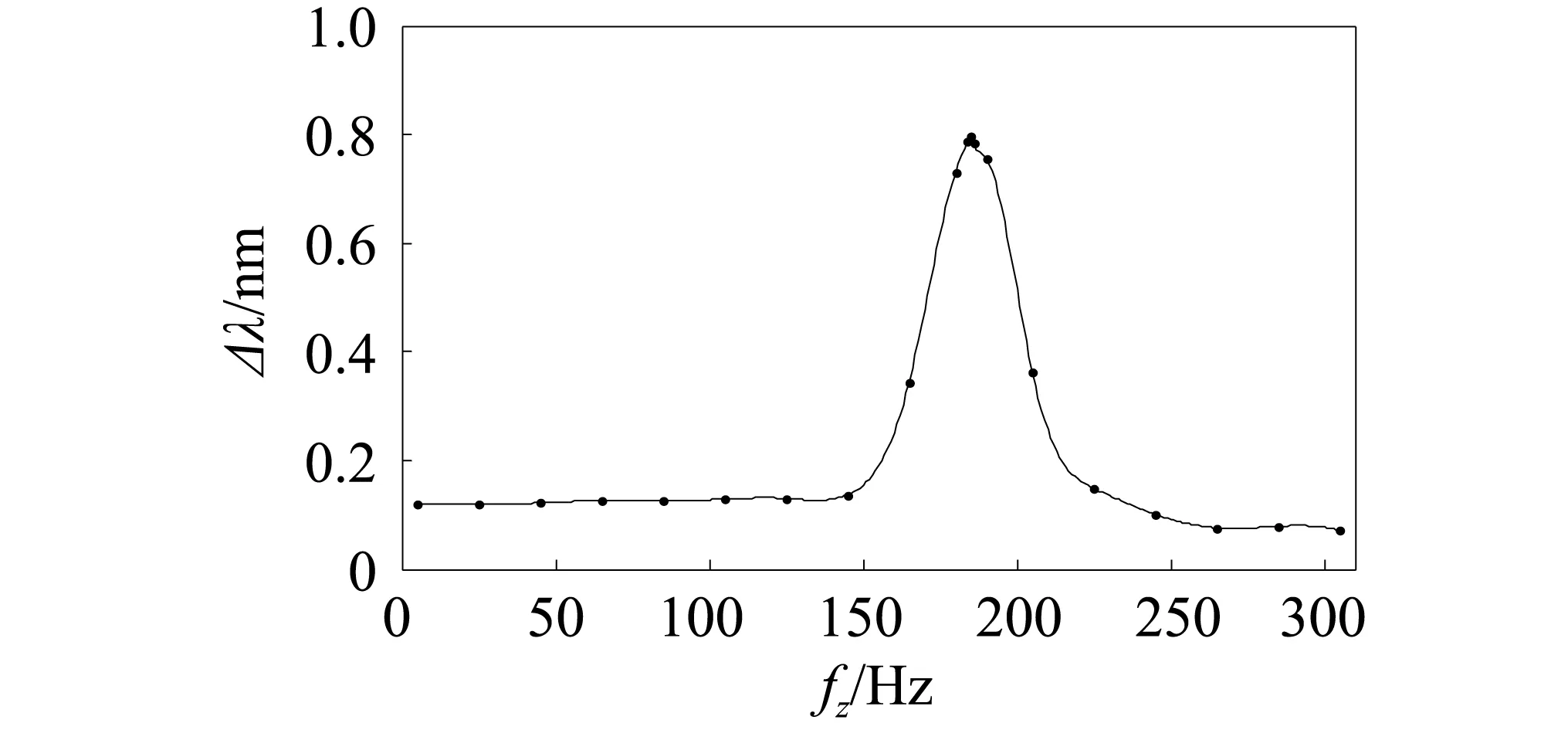
图11 传感器频率响应拟合曲线Fig.11 The sensor frequency response fitting curve

由图可得，在频率为150 Hz左右时，振动传感器中心波长的偏移量有增大的趋势；达到165 Hz左右的时候，其偏移量突然骤增；在185 Hz左右时，偏移量达到最大，说明此时FBG振动传感器出现共振效应，所以能够得到该传感器固有频率大约是18 Hz，与传感器的固有频率仿真分析结果是185.18 Hz，进一步验证了该传感器的结构设计的可靠性。

(5)FBG振动频率传感器横向抗干扰性实验

因为在载荷的作用下，以往单等强度悬臂梁将出现转角以及挠度，同时其抗扭能力比较差，所以传感器性能在很大程度上得到了限制。而双等强度悬臂梁式传感器能够很好地克服以往单梁结构的不足增强其抗干扰能力。在实验过程中，分别施加5 m/s2的加速度在传感器水平振动方向与工作振动方向，实验测试时，控制振动台的振动频率由10 Hz以10 Hz的步长持续增加至100 Hz，并记录下传感器的中心波长漂移量。

以在不同方向上测振时，传感器的中心波长漂移量为纵坐标；以振动台的振动频率为横坐标，利用试验数据在相同的坐标系内分别作出与之对应的拟合曲线，如图12所示。

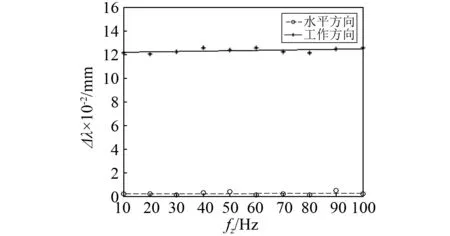
图12 传感器横向抗干扰性试验曲线Fig.12 Horizontal anti-interference curve of the sensor

从图12能够得到，在工作振动方向上，FBG振动频率传感器的中心波长漂移量大约在0.121～0.126 nm范围内；但在水平振动方向上，FBG振动频率传感器的中心波长漂移量非常小，基本为0.001～0.005 nm。因此，本文设计的FBG振动频率传感器有着很好的横向抗干扰性。

4.3 轴向柱塞泵振动频率测量实验与分析

自行搭建斜轴式轴向柱塞泵频率测量系统，将FBG振动频率传感器粘贴于柱塞泵左侧泵体侧面中心位置处，并将其接入解调设备，如图13所示。设置油液压力14 MPa，控制电机转速为1 500 r/min。

图13 左侧泵体侧面中心位置频率测量实验Fig.13 Experiment on the center position frequency measurement of the left side pump body.

时域曲线经过傅里叶变化及巴特沃斯滤波求得的频率值大小，如图14所示。

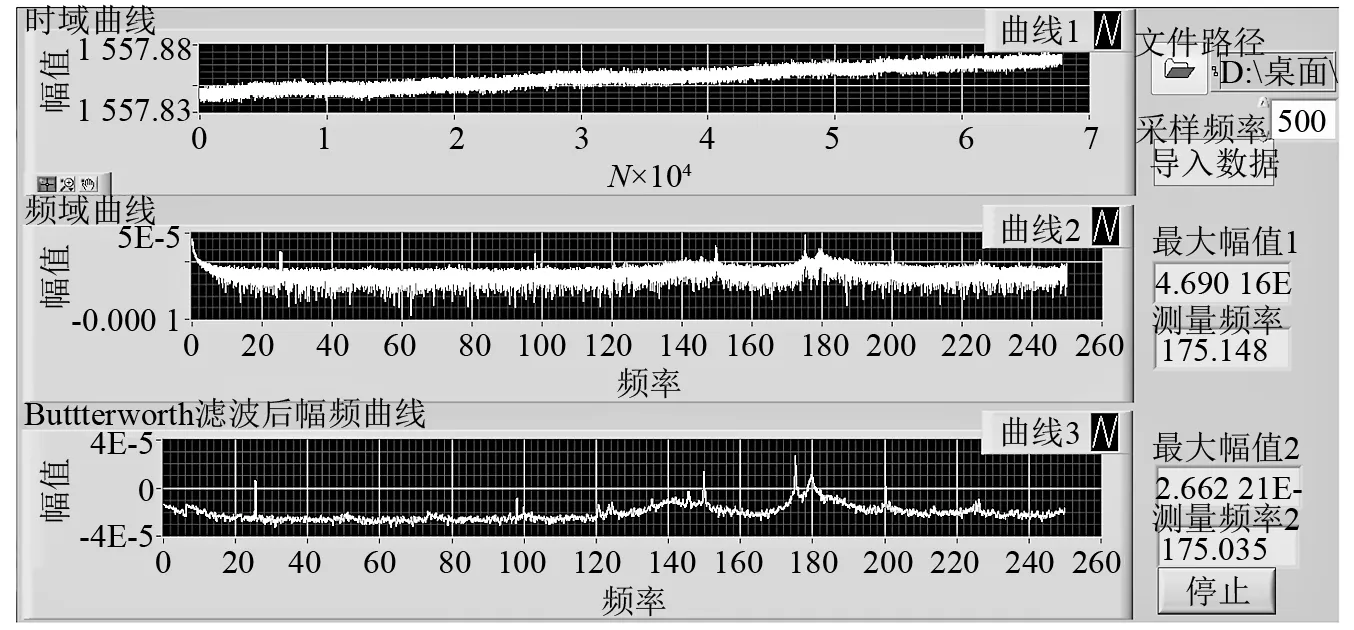
图14 左侧泵体侧面中心位置频率测量结果Fig.14 Frequency measurement of the center position of the left side pump body

从图14可知，柱塞泵以1 500 r/min的转速工作时，振动频率为175.035 Hz。从时域曲线中，可以看出，FBG中心波长随时间而略微增大，这是由于随着柱塞泵的运转，泵体侧面区域温度有所升高，由于FBG的温度传感特性，致使FBG中心波长略微增大，但这并不影响时域曲线携带的频率特性。

由光纤传感理论可知温度会对光纤光栅应变结果具有交叉耦合，但由于振动量是由中心波长量经傅里叶变化获得的，因此温度对振动测量的影响忽略不计。为进一步说明温度对振动测量的影响作用，开展试验研究。液压系统中液压油正常工作温度范围通常为[20℃～70℃]，本文主要考虑此温度范围内对振动测量结果。液压系统压力及转速等条件不变的情况下，不同时间段进行柱塞泵振动频率测量，液压油温度会升高，可测得不同油温条件下振动频率值。图15和图16分别给出了油温为23℃和55℃情况下的振动频率值。

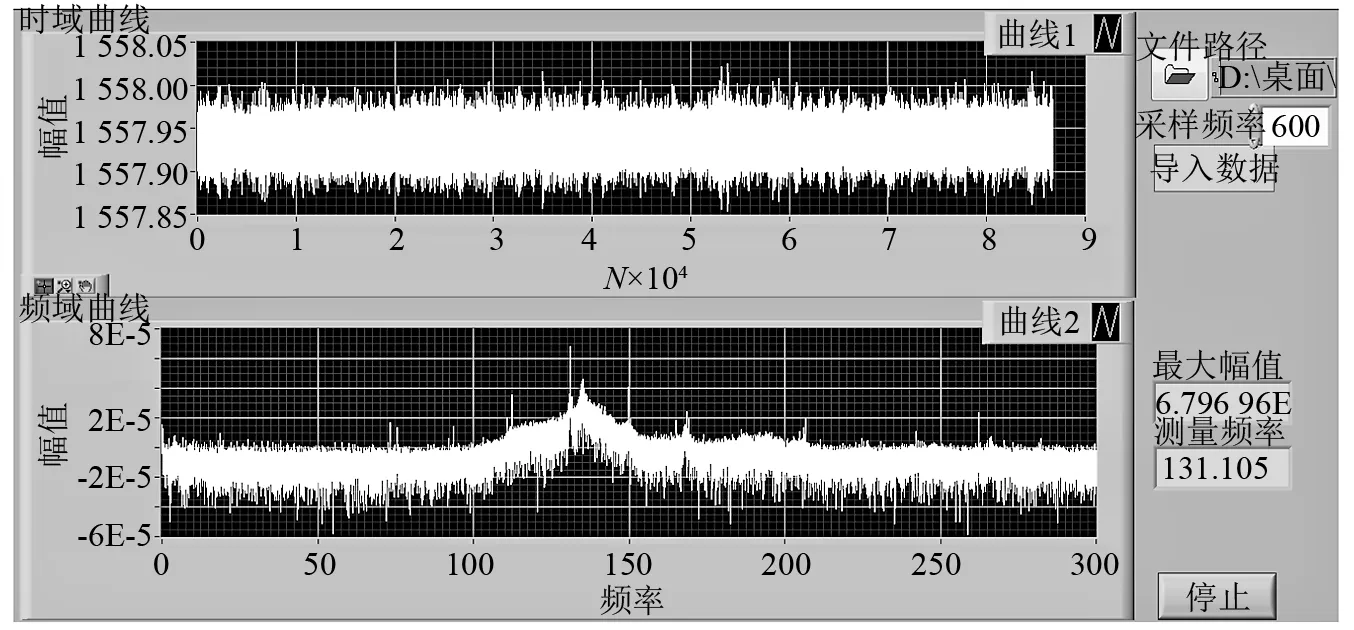
图15 油温为23℃下的振动频率Fig.15 Vibration frequency under oil temperature at 23℃

图16 油温为55℃下的振动频率Fig.16 Vibration frequency under oil temperature at 55℃

对比图15和图16可知，不同温度下(23℃与55℃)的柱塞泵振动频率，时域曲线出现上下移动，且温度越高光纤光栅中心波长变化越大，但频域曲线并没有发生变化，进一步说明了温度的变化基本不影响频率特性的测量结果。

改变电机转速，分别记录在1 500 r/min、1 200 r/min、900 r/min和600 r/min转速状态下，不同点位三次采样时，FBG振动频率传感器测量频率值，如表3所示，f1表示FBG振动频率传感器在柱塞泵左侧泵体侧面中心位置时的三次频率测量平均值，f2表示FBG振动频率传感器在柱塞泵左侧泵体端面边缘位置时的三次频率测量平均值。

表3 频率理论值与实测值数据Tab.3 Theoretical and measured data of frequency

从表3能够得到，待测频率理论值同实验测试结果吻合度较好。说明解调系统能够高精度求解双等强度悬臂梁式FBG振动频率传感器所感应的待测振动信号，并通过分析计算，很好地显示了频率测量结果，重复性较好，测量可靠性较高。

5 结 论

本文首次将FBG传感技术引入到轴向柱塞泵的非介入式振动信号测量中，为液压系统状态监测与故障振动打下基础。在振动传感器设计的基础上，通过仿真与试验的方法均验证了传感器设计和传感系统的可靠性，优点如下：

(1)利用光纤传感技术测量机械设备的振动，较传统振动传感器可以有效避免电磁干扰，可靠性与灵敏度高、易表面粘贴，实现非介入式测量；

(2)在传感器设计方面，采用了双等强度悬臂梁式结构，提高固有频率和抗干扰能力的同时，工作频带也得到了拓宽，振动传感器能够采集更丰富的振动信号。