磁流变阻尼器对火炮后坐炮膛时期阻尼特性分析

张 广， 汪辉兴， 王 炅

(南京理工大学 机械工程学院， 南京 210094)

磁流变胶(MRG)是磁流变智能材料的一种，由微米或亚微米软磁材料颗粒(纯铁、羰基铁、镍等)按一定比例均匀分散在高分子(如聚氨酯、硅树脂等)无磁性基体中形成的一种具有如下流变特性的多态智能材料：无外加磁场下具有较好的流动性，材料力学特性表现为均匀的各项同性；一旦施加磁场，其内部结构发生快速、连续变化，颗粒沿磁场方向排列成链柱状或网状，材料力学特性表现出明显的各向异性，具有一定的屈服强度，撤离磁场后又恢复原来的状态[1-6]。其基体为三维网络结构的高分子材料，因此，MRG具有比MRF更好的抗沉降性和抗聚集性；另外，由于基体黏度比硅油大，因此，以MRG为介质的器件密封结构简单。基于以上性质，又由于其具有耗能低、适应温度范围广、低污染、易控制等特点[7-8]，可广泛应用于各种悬架减振系统、光学球面透镜抛光、触觉传感、直升机起落架减振等[9-12]。

传统火炮的反后坐装置的流液阻尼通道面积通常为常数或者是缓冲行程的函数，难以根据外部射击条件以实时改变自身阻尼变化规律，无法满足现代战争中应用环境多变性对火炮技术性能提出的要求[13-16]。基于磁流变智能材料具有良好的机电耦合特性，逐渐在抗振冲控制中取得良好的效果，也为复杂条件下的机电系统的冲击缓冲控制设计提供了可能[17]。其中，王炅等[18]较早提出将磁流变阻尼器应用到火炮反后坐中；建立了磁流变阻尼器的动力学模型，并讨论了磁流变阻尼器在火炮反后坐装置上的应用。随后，该团队又针对火炮炮膛合力冲击下磁流变减振器的动态特性展开研究[19]；王炅等[20-22]针对磁流变阻尼器用于火炮反后坐装置的结构设计及控制方面取得了丰硕的成果。李赵春等[23]针对某型号火炮设计了反后坐用磁流变阻尼器，并进行了5种不同电流下的动态测试，验证了该阻尼器对反后坐控制的可行性。朱超等[24]针对某型号火炮建立动力学模型和电磁模型，并设计了磁流变后坐系统，提出了PID和模糊控制算法。Ahmadian等[25]设计了适合高速用的火炮反后坐磁流变阻尼器，建立了反后坐过程动力学模型并对其进行高剪切试验，印证了磁流变阻尼器运用于火炮反后坐可能性； Bajkowski等[26-27]研究了磁流变缓冲器用于AKMS卡宾枪的后坐减振系统中的缓冲性能； Singh等[28]以火炮开火时后坐载荷最小化和火力最大化为控制目标，提出了一种多目标优化问题，考虑弹簧在内的后坐磁流变减振器的力学模型，通过评估压力来预测阻尼器反冲力; Akiwate等[29]设计了用于火炮反后坐磁流变阻尼器，测试了其力学性能，并将其与传统被动制退机为基础的火炮减振装置进行输出力学性能的比较。

以上学者针对以磁流变液为动力传递介质研制的阻尼器应用于火炮反后坐的可能性、力学特性、阻尼输出性能等展开研究，宏观上反映阻尼器运用在武器系统的可行性，而没有对可控的微观机理展开进一步分析。基于磁流变材料的微观流变特性对阻尼器的宏观输出阻尼性能具有非常重要的影响；因此，为了得到磁控微观流变力学特性如何调控阻尼器宏观输出阻尼的机理，进一步深入了解它们之间的本质关系，本文以火炮后坐过程炮膛时期炮膛合力冲击作用为分析背景，建立后坐过程中阻尼通道的平行板模型，针对该模型在混合流动模式(阻尼器实际工作状态)下，理论分析MRG微观力学性能与阻尼器宏观阻尼输出的关系，最后利用MRG-70力学参数对阻尼器应用在火炮反后坐炮膛时期的可控性展开初步分析。

1 实验样品制备与模型参数识别

1.1 硅树脂基磁流变胶制备

1.1.1 材料

改性环氧硅树脂的合成分为三个步骤[30-31]:首先，如表格1所示的材料通过缩聚反应生成含有羟基或乙氧基的有机硅低聚物(中间体)；其次，在催化剂的作用下，将第一步所得的有机硅中间体与环氧树脂在溶剂中进行缩合反应生成改性环氧硅树脂，其材料的具体参数如表2所示。最后，将羰基铁粉末 (型号: JCF2-2, 吉林吉恩镍业有限公司，中国，平均直径为5 μm)作为磁性颗粒与硅树脂基质均匀混合。

1.1.2 试样制备

硅树脂基磁流变胶(MRG)的制备流程示意如图1所示。制备过程分为三步：分别是有机硅低聚物(中间体)的制备、改性环氧硅树脂的制备(成品)和硅树脂基的磁流变胶的制备。

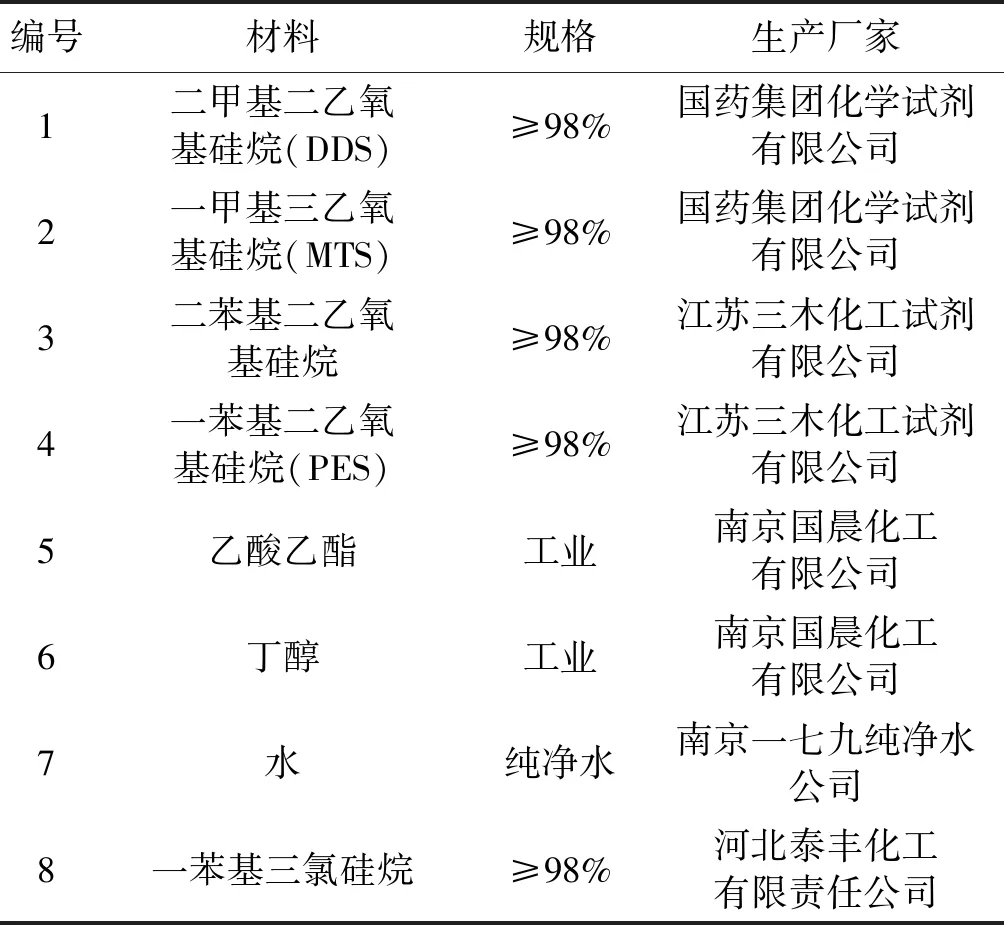
表1 缩聚产生有机硅低聚物所需材料Tab.1 Materials was used to produce organic silicon oligomer

表2 聚合产生改性环氧硅树脂所需材料Tab.2 Materials was applied to prepare a modified epoxy silicone resin

根据羰基铁粉质量分数将该MRG命名为MRG-70。并对制备后的MRG-70进行电镜扫描，观察内部碳基铁粉分布均匀性，结果如图2所示。

图1 硅树脂基磁流变胶制备流程Fig.1 Preparation process of silicone-based MRG

图2 MRG-70电镜扫描Fig.2 Scanning electron microscopeof MRG-70

由图2可知，羰基铁粉(球体)的直径分布在200 nm～3 μm之间，自制MRG-70中的羰基铁粉均匀分布在硅树脂基质中。

1.2 Bingham model参数识别

通过商用流变仪(型号：Anton Paar MCR physica 301)在室温下(25℃)分别测量了MRG-70在磁感应强度为B=[0,131,264,528,1 056]mT的流动曲线，其中剪切速率的变化范围为：0～100 s-1，结果如图3所示。

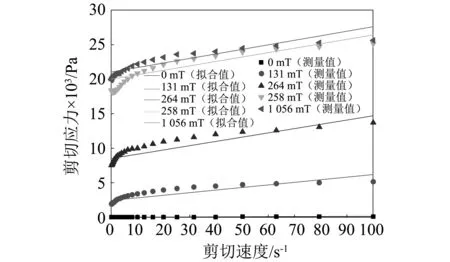
图3 不同磁场下MRG-70的流动曲线Fig.3 Flow curves at different magnetic induction intensity for MRG-70

由图3可知，对于不同磁场下，MRG-70屈服后的剪切应力与剪切速率的关系近似满足线性变化。剪切应力(剪切速率接近0时对应的剪切应力)随着磁场的增强而增大。基于以上分析，MRG-70为非牛顿流体，其本构特性可以用简单的Bingham模型[32-34]描述:

(1)

图3也给出了Bingham模型拟合结果，不同磁场下模型参数识别，如表3所示。

表3 不同磁场下Bingham模型参数识别结果Tab.3 Each parameter value of Bingham model at different magnetic induction intensity

2 磁流变火炮反后坐缓冲系统动力学分析

火炮发射时，引起火炮后坐运动的主要动力是火药气体作用下的炮膛合力，该作用力时间短暂，大约为几十毫秒，但对炮身的作用是非常复杂的，为了便于分析，将炮膛合力分为两个阶段：炮膛时期(研究对象)和火药后效期，图4为某型号固定式火炮炮膛合力随时间变化曲线[35]。

该炮膛合力时间特性曲线中的炮膛时期炮膛合力Fpt1通过以下式子表示[36-38]：

(2)

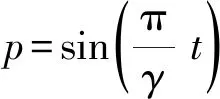
图4 某型号固定式火炮炮膛合力随时间变化曲线Fig.4 The curve of time of bore resultant force of a certain type of fixed artillery

由图4曲线可以看出，该型号火炮发射时炮膛时期具有作用时间短、变化剧烈、峰值高等特点，因此，需要通过反后坐装置将冲击能量在后坐过程中有规律耗散。图5为自行设计的磁流变缓冲器应用在该型号火炮后坐部分受力示意图。

图5所示，发射时后坐部分所受的主动力为炮膛合力Fpt1和后坐部分重力mhg，它们分别作用在炮膛轴线和后坐部分质心上。此外，约束反力包括磁流变缓冲器阻力FMR，复进机力Ff和它们密封装置的摩檫力F，以及摇架导轨的法向力FN1,FN2和相应的摩檫力FT1,FT2。摇架导轨上的总摩檫力为：

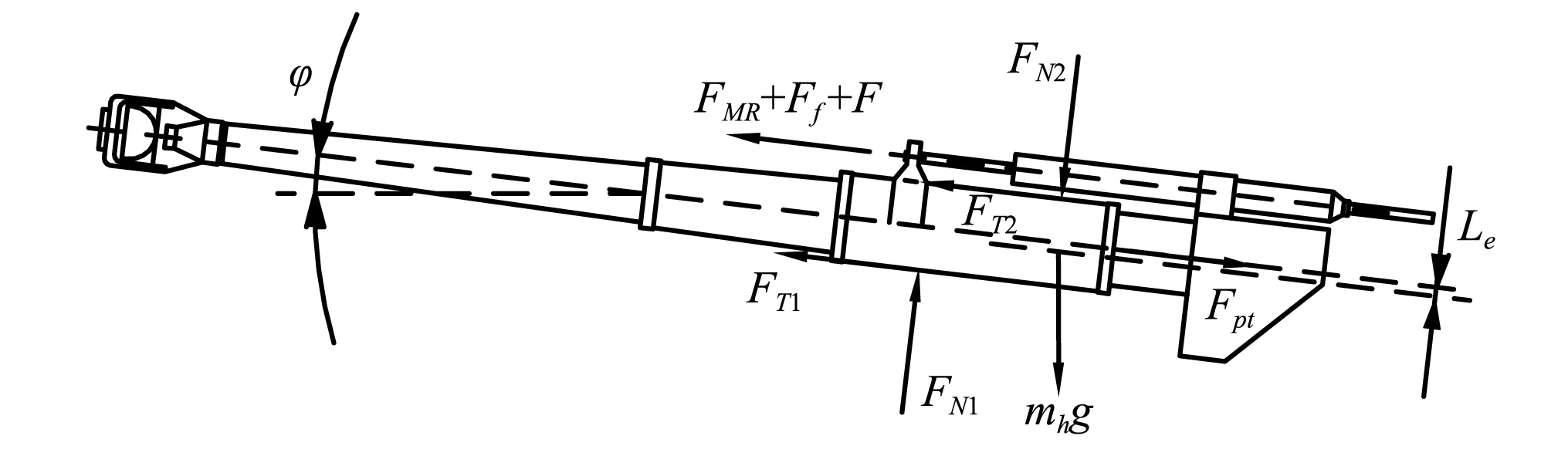
图5 磁流变缓冲器火炮后坐部分受力示意图Fig.5Schematic diagram of force of recoil part of artillery of magneto rheological damper

(3)

式中：f为摇架导轨的摩擦因数。

根据质点的达朗贝尔原理，作用于后坐部分的主动力、约束力和惯性力组成一平衡力系，故火炮后坐运动微分方程可以表达为：

(4)

式中：X为后坐行程，φ为火炮高低射角。

由于火炮反后坐过程十分复杂，耦合磁流变阻尼器后又增加了研究的复杂性，因此，在磁流变反后坐模型中不考虑火炮后坐时复进过程[22]，图6给出磁流变火炮反后坐运动单自由度动力学模型。

图6 磁流变火炮反后坐单自由度动力学模型Fig.6 The dynamic model of a single degree of freedom for anti-recoil of MR artillery

由于人们对火炮后坐过程中炮膛时期炮膛合力的研究的理论较为深入，而对后效期炮膛合力的理论还是基于各种假设以及实践应用中还是靠经验公式计算。因此，以下主要针对火炮后坐运动炮膛时期磁流变阻尼器的阻尼特性展开分析。根据图6，磁流变火炮反后坐动力学微分方程可描述如下[39]：

(5)

炮膛时期火炮后坐由静止开始运动，因此边界条件如下：

(6)

式中：CBm为磁流变阻尼器有效阻尼系数，与磁场强度有关。

在图4所示的炮膛时期炮膛合力变化规律作用下对式(5)进行积分并代入边界条件得到后坐炮膛时期运动位移随时间解析式如下：

(7)

对于特定型号火炮在特定发射状态，其质量mh，高低射角φ都是已知的，炮膛时期的炮膛合力Fpt在前面已经求得，唯一不知道的是磁流变阻尼器有效阻尼系数CBm。又由于火炮后坐炮膛时期，其后坐合力大、作用时间非常短且变化剧烈，因此在以下部分主要分析在条件Δp≫v(强磁场下或大屈服应力下)的情况下，磁流变阻尼器阻尼系数CBm。

3 火炮反后坐磁流变阻尼器阻尼系数分析

建立阻尼器工作下阻尼通道内部的平行板模型，针对平行板模型工作在库埃特(Couette)剪切流动和泊肃叶(Poiseuille)压力流动组成的混合流动模式(阻尼器实际工作状态)的情况，分析了Bingham本构模型下阻尼器的阻尼效果，并求得了阻尼器阻尼系数CBm。表4给出Bingham流体在混合模式下的边界条件，其中各符合代表意思将在以下分析中说明。

表4 阻尼器平行板混合流动模型边界条件Tab.4 Boundary conditions for a mixed flow model of a damper parallel plate

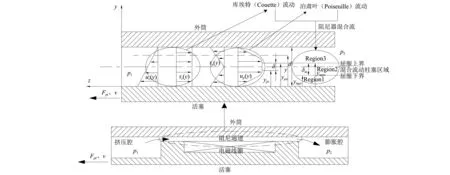
图7 阻尼通道内Bingham本构流体混合流动平行板模型Fig.7 A parallel plate model of Bingham constitutive fluid flow in the damping channel

以活塞左端为原点、活塞运动方向为轴建立如图7所示直角坐标系。阻尼器受外力Fpt以速度v运动，流体在阻尼通道内部的流动非常复杂，该模型描述的是连续发展的准稳态流动，包括Couette剪切流动和Poiseuille压力流动(以下简称剪切流动和压力流动)。在混合流动平行板模型中具体描述为：剪切流动是在不存在压力差的情况下，由于一个极板(活塞)运动而带动流体运动，其运动方向与极板运动方向相同；压力流动是由于平行极板出入口存在压力差引起的运动；在阻尼器中与活塞运动方向相反。因此，阻尼器中阻尼通道的流体流动为剪切流动和压力流动的混合流动。另外，值得注意的是:在实际阻尼器中由于活塞产生运动，流体不断从挤压腔流向膨胀腔，因此，在分析过程中可以认为阻尼通道流体流动方式主要以压力流动为主，而剪切流动对其阻尼通道的特点区域有着不可忽略的影响。

图7为Bingham本构流体在阻尼通道压力流动的平行板模型，该状态下的本构方程可以描述如下[32]：

(8)

在图7中可知，Bingham本构流体在阻尼通道混合流动下，其柱塞流区域分布与纯压力流动下不一样，由于活塞本身的运动引起的额外剪切应力导致Region1内流动发生变化，进而改变ympi处的边界条件(如表4所示)。对Region2柱塞流的影响可以描述如下：在压力流动的基础上施加了活塞运动引起的剪切应力；在MRG-70的剪切屈服应力、外部压力差以及阻尼器结构尺寸不改变的情况下，与纯压力流相比，ympo的位置及ympo处的边界条件不发生变化。基于以上分析，Region3的流动情况与在纯压力流的情况一致。具体分析如下:

Region1:

此区域为屈服后区域，平行板模型下该区域的流速为纯剪切流动和纯压力流动时阻尼通道流速分布的矢量和，由于它们的流速方向都是轴向方向，在其余的方向不发生流动，因此该区域的流速可描述如下：

(9)

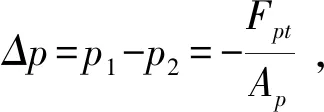
(10)

Region2:

由于外力作用形式以及阻尼器几何形状不变，因此Bingham本构模型下的平行板间应力分布情况与Newtonian流体一致：

(11)

将表4所列边界条件代入式(11)并整理得出屈服前柱塞流动y轴方向宽度δm：

(12)

通过之前分析得出混合流动柱塞区屈服上界与压力流动一致，而剪切流动主要影响屈服下界位置以及Region1流动特性；因此，混合流动中柱塞流边界关系：

(13)

联立方程式(12)和式(13)得：

(14)

对式(14)进行无量纲化处理得：

(15)

Region3:

根据式(9)分离出Bingham流体在平行板间的压力流动流速分布方程：

(16)

将表4所列边界条件代入式(16)得到Bingham流体在阻尼通道混合流动的平行板模型中Region3中流速分布方程：

(17)

将式(14)分别代入式(10)和式(17)得平行板模型中各区域的流速方程：

(18)

将式(18)代入式(8)得出平行板模型各区域剪切应力分布方程：

(19)

(20)

对比式(20)和式(8)(结构一致)，得出Bingham系数Bi的表达式如下：

(21)

根据式(12)得出剪切屈服应力表达式：

(22)

将式(22)代入式(21)得出平行板模型中Bingham流体下炮膛合力引起的活塞运动速度的表达式：

(23)

活塞在炮膛合力Fpt的作用下运动，受到的阻尼力为CBmv，其中CBm为Bingham流体工作在混合流动模式下阻尼器的阻尼系数；则从动力学方面考虑，得出力与速度的关系为：

Fpt=CBmv

(24)

将式(23)代入式(24)得出混合流动模式下阻尼器的有效阻尼系数表达式：

(25)

混合流动模式下阻尼通道平行板模型中各区域流量为：

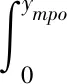
(26)

式中：W=2πR1；阻尼通道平行板模型中流量之和为QBm=QBm1+QBm2+QBm3，则：

(27)

由于活塞运动时其有效面积挤压压缩腔引起的流量与阻尼通道平行板模型中流量之和QBm相等，方程表达如下[39]：

QBm=Apv=QBm

(28)

当Δp≫v(强磁场下或大屈服应力下)时，式(28)可以简化为：

(29)

将式(23)和式(29)代入式(28)得出Bingham系数Bi：

(30)

式中：Ad=Wd为阻尼通道截面积。

综述以上分析，表5给出平行板模型中混合流动模式下Bingham本构流体在阻尼通道流动产生的阻尼器的阻尼系数。

表5 混合流动模式下Bingham本构流体阻尼通道流动产生的阻尼器的阻尼系数Tab.5 The damping coefficient of the damper in Bingham constitutive fluid damping channel flows under mixed flow mode

4 磁流变阻尼器对火炮后坐炮膛时期位移可控理论仿真分析

由于Bingham本构模型流体工作在混合模式下最接近阻尼器实际工况，因此以下针对不同磁场下MRG-70在阻尼通道中的混合流动产生的阻尼器有效阻尼对火炮后坐位移运动的可控性展开初步探索性分析。所设计的磁流变阻尼器基本机构及尺寸，分别如图8和表6所示。

表6 阻尼器基本尺寸Tab.6 The basic size of the damper

图8 阻尼器基本结构Fig.8 The basic structure of the damper

图9给出磁感应强度分别在0，131，264，528，1 056 mT时，火炮高低射角为60°情况下后坐炮膛时期位移运动情况。

图9 不同磁场下火炮后坐炮膛时期位移运动情况Fig.9 The displacement of the artillery recoilduring bore period under different magnetic fields

从图9可知，当火炮后坐受炮膛合力的作用下，后坐装置发生位移，位移方向与炮膛合力方向同向。在不加磁场控制的情况下，由于炮膛合力引起的后坐位移随时间变化剧烈，仅仅在炮膛时期(大约为10 ms)就从0迅速增长到95 mm；随着引入磁场控制，在外加磁感应强度为131 mT时,后坐受炮膛时期的炮膛合力作用下仅仅移动了3.5 mm,可控性为91.5 mm(定义可控性为磁场引起的位移变化)；而继续增强磁感应强度，后坐位移变化不明显，从131mT增强到1 056 mT后，后坐位移从3.5 mm下降到了2.5 mm，可控性为1 mm。图9中阴影部分代表可控区域。为了便于观察，图9中小窗口给出了磁感应强度在131mT后阻尼器对后坐位移的控制曲线。通过以上分析，说明利用磁流变阻尼器来控制火炮后坐过程的可行性，并且能力消耗非常小(大部分阴影面积在磁感应强度为0～131 mT曲线之间)。

值得一提的是：在图9中，还观察到不加磁场控制情况下，由于在炮膛时期刚开始的瞬间由于弹丸对炮膛内壁的摩擦作用带动后坐前倾，因此刚开始位移为负数，这个后坐前倾作用严重影响了火炮发射的精度；而加入磁场控制后，由于MRG-70具有剪切屈服应力，因此能够起到抗前倾的作用，具体控制机理有待展开深入研究。

5 结 论

研制了MRG-70，并对其流动特性展开测试，以火炮后坐过程为研究背景，理论分析了阻尼器的阻尼特性；最后将MRG-70的流动特性参数代入理论分析结果中对磁流变阻尼器应用在火炮反后坐的可控性展开初步分析，结果如下：

(1)对于不同磁场下，所研制的MRG-70的本构特性可以用Bingham模型描述；

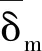
(3)MRG-70磁流变阻尼器对火炮后坐炮膛时期具有可控性，且在能量输入非常小(0～131 mT)的情况下能达到较宽的可控范围。