主动谋变,变中求通——对一道教材课后习题变式拓展的思考

江苏省苏州市吴中区迎春中学(215128)凌勤霞

一、前言

书本上的习题是数学教材的重要组成部分,是通过专家们精心构思,反复斟酌推敲设计出来的,具有不容置疑的典型性、示范性和探索性.课后习题一方面能使学生巩固所学的新知识,学会运用新知识解决实际问题,另一方面它有助于学生掌握和运用数学思想、方法、发展学生的数学思维,从而促进学生数学核心素养的提高.因此,如何恰当地运用课本习题,如何充分地挖掘和深化这些习题,使其发挥内在潜能,以培养高素质的学生,是教师面临的一个新课题.

结合笔者十多年的一线数学教学实践,对教材中习题的拓展和开发作了一些尝试,旨在让学生通过“主动谋变”实现“变中求通”,提高学习数学的能力.

二、教材原题

(苏科版九年级下册59 页第3 题)

如图1,在正方形ABCD中,E是AD中点,点F在CD上,且CF=3FD.△ABE 与△DEF相似吗? 为什么?

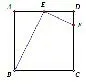
图1

解读这是教材中“探索三角形相似的条件”这一小节中的一道课后习题,考查了“两组对应边的比相等且夹角对应相等的两个三角形相似”这一判定方法,也考查了正方形的性质,属于基础题,学生很容易证得结论.

发现这道习题本身很容易解决,但其中蕴含了一个很重要的数学基本图形“K字型”(如图2).近年来,许多中考题围绕此基本图形进行命题.因此我们可以这道习题为蓝本,对它作进一步的挖掘、引申和探索,找出新的生长点,这对提高课堂效率、提高学生的数学素养、发展学生的学习能力能起到事半功倍的效果.

图2

三、变式拓展

3.1 直接变式,感知模型

例1(1)如图3,在正方形ABCD中,E是AD上任意一点,点F在CD上,且BE⊥EF,△ABE 与△DEF 相似吗? 为什么?

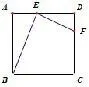
图3

(2)如图3,如图,E是正方形ABCD的边AD上的动点,EF⊥BE 交CD于点F.若正方形的边长为4,AE=x,DF=y.则y与x的函数关系式为_____.

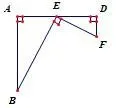
图3.1

说明例1(1)对原题作了条件上的变化,图形不变,考察学生用定理“两角分别相等的两个三角形相似”证明相似,以此巩固新知.例1(2)在(1)的基础上将其中点E设置为动点,加入函数元素.要求y与x的函数关系,实际上只要证明两个直角三角形相似,由相似三角形对应边成比例即可求得结果.解题完毕后可以让学生观察图中两个直角三角形的摆放位置,引导其发现将它们拼在一起后构成了第三个直角,让学生感知“K字型”的基本模型：

条件：A、E、D 三点共线,∠A=∠D=∠BEF=90°;结论：△ABE～△DEF.

3.2 改变背景,巩固模型

例2已知C、D是一段圆弧上的两点,它们都在直线l的同侧,过这两点分别作直线l的垂线,垂足分别为A、B.E是BC上一动点,连结DE、CE、CD,∠CED=90°.

(1)如图4①,若AD=6,AE=4,BE=12,求CD的长.

(2)如图4②,若点E恰为这段圆弧的圆心,则线段AB、BC、AD之间有怎样的等量关系? 请写出你的结论并予以证明.

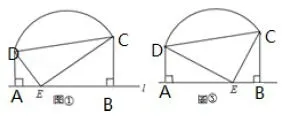
图4

说明本题增设了圆的背景,将基本图形与圆、动点巧妙地结合在一起.(1)中根据基本图形证得相似,利用相似三角形对应边成比例即可求出线段长.本题在几何计算中比较常见,具有典型性.(2)中将E 点设置为圆弧的圆心,便可挖掘出CE=DE这个重要条件,基本图形加上这个条件,便可碰撞出新的火花——两个直角三角形全等.这是“K字型”的特例.

例3如图5,平面直角坐标系中有一个矩形纸片OBCA,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.

(1)如图5①,当∠BOP=30°时,求点P的坐标;

(2)如图5②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,求m(用含有t的式子表示).

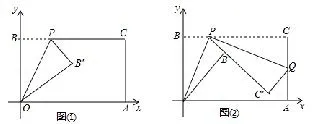
图5

说明本题将原来的正方形问题改变成了平面直角坐标系中的矩形纸片折叠问题.引导学生发现,第二小题中通过两次折叠纸片,构造出了“K字型”的数学模型,这样就找到了△OBP与△PCQ这对三角形相似.再结合折叠性质、矩形性质、勾股定理等知识来解决问题,增加了题目的综合性,巩固了数学模型.

3.3 类比迁移,推广模型

在掌握了前面归纳的出现三个直角构成的“K 字型”后,继续拓展演变,可将其中的“三个直角”条件变为“三个角相等”,由两个直角三角形相似迁移为两个普通三角形相似.

例4如图6,等边三角形ABC的边长为4,点P为BC边上一点,且BP=1,点D为AC边上一点.APD=60°,求CD的长.

例5如图7,等腰直角△ABC 的直角边长为4,P为斜边BC上一点,且BP=1,D为AC上一点,若∠APD=45°,求CD的长.

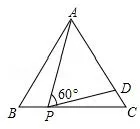
图6

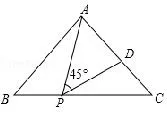
图7

说明上述两个例题是将“三个直角”条件分别改变为“三个60°角”、“三个45°”这样的特殊角,解决这两题的关键是要推出△BAP～△CPD.如何证相似,则可与前面归纳得到的“K字型”进行类比,利用等边三角形性质、等腰直角三角形和三角形外角性质,找出它们的相同点与不同点,从而将“K 字型”进行推广,提高学生类比猜想能力.

例6 如图8,在平面直角坐标中,四边形OABC是等腰梯形,CB//OA,OA=7,BC=1,AB=5,点P为x轴上的一个动点,点P不与点O、点A重合.连接CP,过点P作PD交AB于点D.

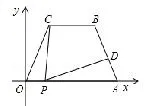
图8

(1)直接写出点B的坐标.

(2)当点P在线段OA上运动时,使得∠CPD=∠OAB,且,求点P的坐标.

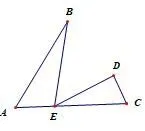
图8.1

说明本题结合了坐标与图形性质、等腰三角形的性质、等腰梯形的性质、相似三角形的判定与性质,具有一定的综合性.其中第二小题,需要证明△OCP～△APD,再根据相似性质求出AP,OP的值.如何证明△0CP与△APD相似? 可引导学生发现本题中也有三个角相等：“∠CPD=∠0AB=∠POC”,虽然它们的度数未知,但是同样可类比前面的方法证明出相似,从而使学生认识到“K字型”的推广模型：

条件：A、E、C 三点共线,∠A=∠BED=∠C=a; 结论：△ABE～△CED.

通过这一系列变式拓展、类比迁移,学生经历了从特殊到一般的思考过程,体验了寻找题目本质的过程,感受到了这些题目不同的仅仅是非本质特征,而本质是一样的.这样的过程锻炼了学生的思维,有效的提高了学生的学习能力,加强了学生数学核心素养的提升.

3.4 充分挖掘,活用模型

数学课程标准》在几何方面要求学生“能从较复杂的图形中分解出基本的图形,并能分析其中的基本元素及其关系,利用直观来进行思考”.要将基本图形从复杂图形中一个个分解出来,需要对基本图形的本质有清晰的认知,能根据某些隐藏的不完整的图形,通过添加辅助线构造出基本图形.

例7如图9,已知点A(-2,1),点B 在直线y=-2x+3上运动,若∠AOB=90°,求此时点B的坐标.

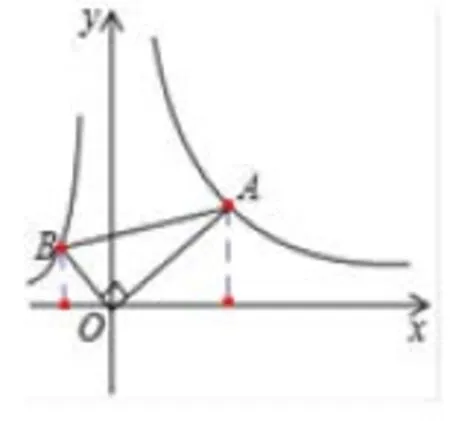
图9

说明本题将问题放在了平面直角坐标系的一次函数和反比例函数中,学生看不到现成的基本图形.要求B 点坐标,需过点B向x 轴作垂线,再引导学生抓住关键条件“∠AOB=90°”,这样便发现了两个直角.已知了A点坐标,要用这个条件就需过点A也作x轴的垂线,于是就出现了第三个直角.随着这三个重要直角的出现,基本图形“K(图9)字型”也就在不知不觉中构造出来了.由前面直接利用基本图形到现在通过添辅助线挖掘出隐含的基本图形,学生对图形的感知得到了发展,进一步提高了数学学习能力.

例8已知抛物线L : y=x2+bx+c 与x轴交于点A和点B(-3,0),与y轴交于点c(0,3),

(1)求抛物线L的顶点坐标和A点坐标.

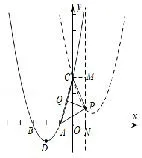
图10

(2)如何平移抛物线L得到抛物线L1,使得平移后的抛物线L1的顶点与抛物线L的顶点关于原点对称?

(3)将抛物线L平移,使其经过点C得到抛物线L2,点P(m,n)(m＞0)是抛物线L2上的一点,是否存在点P,使得△PAC 为等腰直角三角形? 若存在,请直接写出抛物线L2的表达式;若不存在,请说明理由.

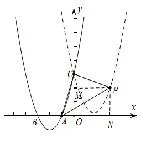
图10.1

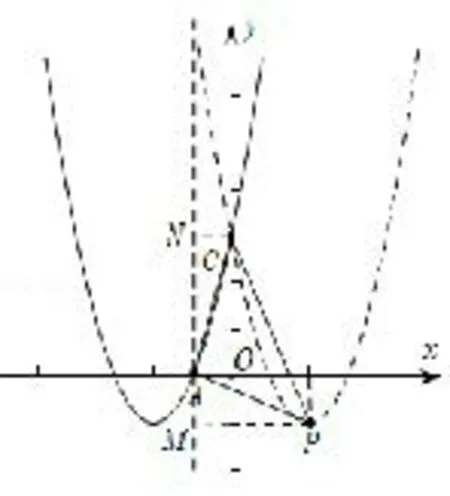
图10.2

说明本题是以二次函数抛物线问题为背景的综合题,问题3是否存在P 使△PAC 为等腰直角三角形并求抛物线L2的解析式,学生对于这类综合题往往找不到抓手,通常会束手无策.教师要引导学生分解图形,抓住本质条件“直角”,分别通过A、C、P作x轴或y轴的垂线段,便可巧妙地构造出“K字型”,然后运用基本图形的知识和方法,为解题思路的探求提供思维方向,灵活地解决相关问题.

四、以变求通

通过对教材课后习题进行变式拓展、巧妙编排,可以达到“做一题,解一类”的目的,可以有效地避免“题海战术”,减轻学生负担,基本打破了“谁作业做的少,谁的成绩就低”的局面,班中部分基础较好的同学成绩反而呈现稳中有升现象.

在平时数学教学中,经常一节课研究一个问题,对其进行一系列的变化,在一次次的变式拓展中,明显感受到学生兴趣较以前增强了.他们会有种新鲜感,会期待着老师还能把这题作怎样的改变,还能结合哪个知识点.学生讨论问题的氛围也形成了,课上没研究完的题目课后会继续探讨,在课堂内及课堂的延续中学生积极参与思考,主动获得解题的思想和方法.

其实,问题一直在变,但不管怎么变,都没有离开一个基本方法或结构.让学生通过学习认识到这种基本方法或结构的存在,主动谋变,变中求通,打开解题思路,从而提升自己的观察问题、思考问题和解决问题的能力.

五、结束语

对一道教材课后习题变式拓展的思考,目的是希望学生从中获得的不仅仅是解答这题本身,而是通过这道题展开了数学“悟”的过程,是一个主动、深度的学习过程.在平时的教学中,作为教师的我们需在遵循《数学课程标准》的前提下,对教学大纲、教材进行深入的研究和分析,多挖掘这种有生长性的习题内涵,抓住习题中的本质因素,拓展其外延.主动谋变,变中求通,在“直接变式,感知模型”中提升自主建构能力;在“改变背景,巩固模型”中提升多元表征能力;在“类比迁移,推广模型”中提升类比推理能力;在“充分挖掘,活用模型”中提升数学运用分析能力,有效地提升数学核心素养.