全等三角形证明中角的转化

湖北省武汉市华中科技大学同济附中(430030)王凯旋

全等三角形的证明和应用是平面几何证明的一个重要开端,线段的转化和角的转化是两个重要的方向,相比较线段转化的明确性,角的转化具有一定的隐蔽性,一些全等三角形的证明中,对应角的相等关系的证明却颇费周折,往往因为不能说明对应角相等而导致不能完成全等三角形的证明.因此,我们需要发掘角的转化的方法,以利于我们更好的完成全等的证明.笔者通过归纳总结,得到如下的几种转化途径.

一、互余转化

利用直角三角形中的两锐角互余或者两个角的和为90°,进行转化,构建角的相等关系.

例1如图1,△ABC中,∠BAC=90°,AB=AC,AN是过点A的一条直线,且BM ⊥AN于点M,CN ⊥AN于点N,求证：AM=CN.

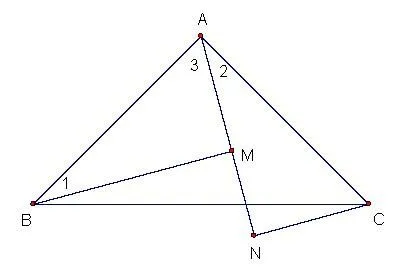
图1

证：因为BM ⊥AN,CN ⊥AN,所以∠AMB=∠CNA=90°,又因为∠BAC=90°,所以∠1+∠3=90°,∠2 + ∠3=90°,所以∠1=∠2.在△AMB和△CNA中,,所以△AMB～=△CNA,所以AM=CN.

二、和差转化

利用几个角的和差运算进行转化,构建角的相等关系.

例2如图2,AD是△ABC的中线,点E在BC的延长线上,CE=AB,∠BAC=∠BCA,求证：AE=2AD.

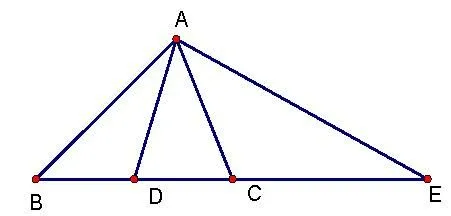
图2

证：如图3,延长AD到F,使AF=2AD,连接CF.在△ABD和△FCD中,

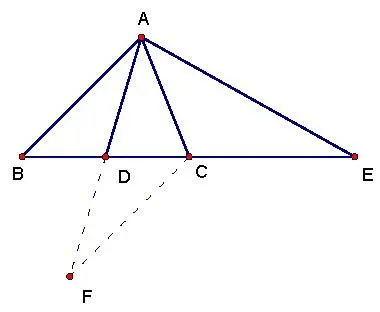
图3

所以△ABD～=△FCD.

所以CF=AB,∠FCD=∠B.

因为∠BAC=∠BCA,∠ACF=∠FCD+∠ACB,∠ACE=∠BAC+∠B,所以∠ACF=∠ACE,因为CE=AB,所以CF=CE.在△ACF和△ACE中,

所以△ACF～=△ACE.所以AE=AF,所以AE=2AD.

三、特殊角转化

利用特殊角之间的和差运算进行转化,构建角的相等关系(可以看做和差转化的特例).

例3已知,如图4,在△ABC中,∠A,∠B的角平分线交于点O,若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60°,求证：OE=OF.

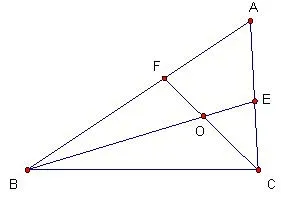
图4

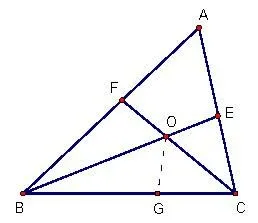
图5

证：如图5,在边上截取BG=BF,连接OG.因为∠A=60°,∠A,∠B,的角平分线交于点O,所以∠BOF=∠COE=60°,∠BOC=120°.因为OB平分∠ABC,所以∠FBO=∠GBO.在△BFO和△BGO中,,所以△BFO～=△BGO.所以OF=OG,∠BOF=∠BOG=60°,所以∠COG=∠COE=60°.因为OC平分∠ACB,所以∠GCO=∠ECO.在△CGO和△CEO中,所以△CGO～=△CEO.所以OG=OE,所以OE=OF.

四、平行转化

利用平行线同位角相等,内错角相等,同旁内角互补,进行转化,构建角的相等关系.

例4如图6,∠ACB=120°,以AC,BC为边向外作正三角形△ACF,△BCE,点P,M,N分 别 为AB,CF,CE的中点.求证：PM=PN.

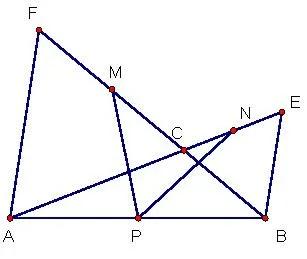
图6

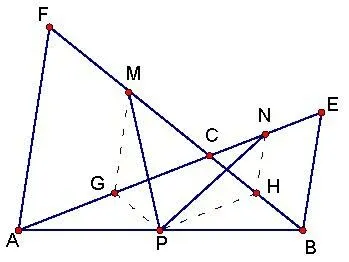
图7

证：如图7,取CB,CA的中点G,H,连接GM,GP,HN,HP.因为三角形△ACF,△BCE是正三角形,所以AC=FC,BC=EC.因为点P,M,N分别为AB,CF,CE的中点,所以所以∠MGC=∠CAF=60°.因为∠ACB=120°,所以所以∠PGC=180° -∠ACB=60°,所以∠MGP=∠MGC+ ∠PGC=120°.同理：,∠NHP=120°,所以MG=PH,PG=NH,∠MGP=∠NHP.在△MGP和△PHN中,,所以△MGP～=△NHP,所以PM=PN.

五、内角和转化

利用多边形的内角和以及三角形外角和内角之间的关系,构建角的相等关系.

例6如阁8，已知＜ BAE 与＜ BCD互为补角，AB=AE,CB=CD，连接ED，点P 为ED 的中点，若点A，B，C不在同一直线上，求证AP ⊥CP.

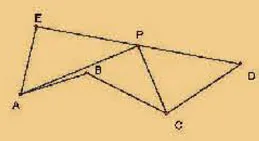
图8

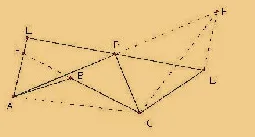
图9

证：如图9，延长AP 到F，使PF=AP，延长CB 交AE 于G，连接AC，DF，CF，在LAEP 和LFDP 中，所以△AEP≌△FDP，所以AE ＝FD，＜E=＜FDP.因为AB=AE，所以AB=FD.设＜ E＜FDP ＝x，＜CDP ＝y，＜BAE＝z，则＜BCD=180°一z .所以＜ CDF=＜CDP+ ＜ FDP=x + y，所以＜EGC=360°- (x + y)- (180°- z)=180° + z 一(x+y)，＜EGC=180°一＜ ABC +z 所以＜ABC=x + y，所以＜ ABC=＜FDC .在△ABC 和△FDC 中，所以△ABC≌△FDC,所以CA=CF，所以AP⊥ CP.

六、综合转化

在一个问题中角的转化的方式不是单一的，而是以上多种方式结合进行角的转化，构建角的相等关系.

例7如图10，AB=AE,AB⊥AE,AD=AC,AD ⊥AC，点M 为BC 的中点，求证：DE 2AM.

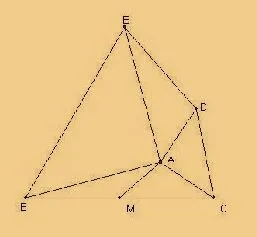
图10

证:如图11，延长AM 到点N，使MN=AM，连接BN，因为点M 为BC的中点，所以BM=CM，在△AMC 和△NMB 中，

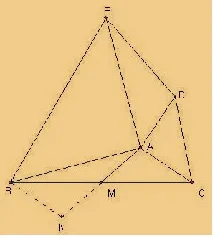
图11

所以△AMC ≌△NMB，所以AC=NB,＜ACM=＜NBM.因为AD＝AC，所以NB＝DE.因为AB⊥ AE,AD ⊥ AC，所以＜ BAE ＝＜ CAD＝90°，所以＜ DAE＝180°－ ＜BAC.因为＜NBA＝＜ABM +＜NBM ＝＜ABM + ＜ACM＝180°－＜BAC，所以＜DAE＝＜NBA.在△NBA 和△DAE中，，所以△NBA ≌△DAE，所以DE=2AM.

在全等三角形判定的证明中角的转化是一个难点.对于部分几何问题，角的转化相比线段的转化都有一定的隐蔽性，对于学生而言，知难而上，克服困难，才能取得进步，而如何克服困难，需要依赖一定的方法通过学习过程中的归纳总结，不失一种好的途径.