联袂解题，魅力无比

甘肃省武威第十中学(733000)张秀丽 陈国玉

将中心投影知识与其他知识融合在同一道题中,是近几年中考的热点考题.这类题不仅提高了试题的趣味性的综合性,而且让试题增添了无穷的魅力.

一、与函数结合判图象

例1如图1,夜晚,小亮从点A 经过路灯C 的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )

图1

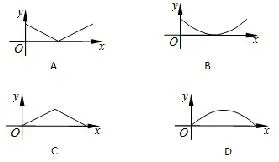
分析等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.利用相似求出y与x之间的函数式,进而结合图象即可找出答案.

解：设小亮身高GE=h ,CF=m ,AF=a,当x ≤ a时,在△OEG 和△OFC中,∠GOE=∠COF(公共角),∠AEG=∠AFC=90°,所以△OEG～△OFC,所以解得,

图2

因为h,m,a都是固定的常数,所以自变量x的系数是固定值,所以这个函数图象肯定是一次函数图象,即是直线;因为影长将随着离灯光越来越近而越来越短,到灯下的时候,将是一个点,进而随着离灯光的越来越远而影长将变大.故选A.

点评本题综合考查了中心投影的特点和规律,解题的关键是利用相似三角形求出y与x之间的函数式.

二、与平面镜联手找光源

例2如图3所示,与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花CD和一棵树AB.晚上,幕墙反射路灯灯光形成了那盆花的影子DF,树影BE是路灯灯光形成的.请你确定此时路灯光源P的位置.

图3

分析由中心投影概念知点光源、物体顶端,物体影子顶端在同一直线上,并结合光的反射定律：反射角等于入射角,可确定出点P的位置.

解：作法如下：如图4所示,

(1)连接FC并延长交玻璃幕于点O;

(2)过点O作直线OG垂直于玻璃幕墙;

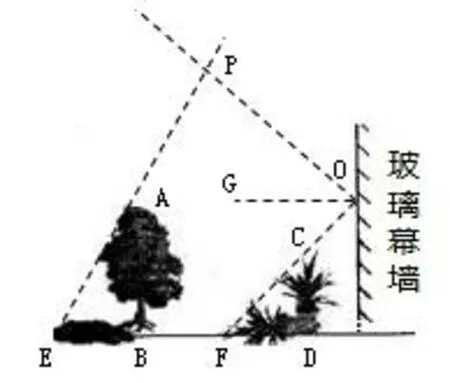
图4

(3)在OG另一侧作∠POG=∠FOG 且交EA的延长线于点P.

所以点P即为此时路灯光源的位置.

点评本题考查平行投影和中心投影的作图,难度不大,体现了学数学要注重基础知识的新课标理念.解题的关键是要知道：连接物体和它影子的顶端所形成的直线必定经过点光源.

三、与相似合作探规律

图5

例3学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图5,在同一时间,身高为1.6m 的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.

(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;

(2)求路灯灯泡的垂直高度GH;

(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长;当小明继续走剩下路程的到B2处时,求其影子B2C2的长;当小明继续走剩下路程的到B3处,…按此规律继续走下去,当小明走剩下路程的到Bn处时,其影子BnCn的长为___m.(直接用n的代数式表示)

分析(1)确定灯泡的位置,可逆用光线画出;

(2)要求垂直高度GH 可以把这个问题转化成相似三角形的问题,利用相似三角形的对应成比例可以求出GH;

(3)和(2)一样也是利用三角形相似,利用对应成比相等可以求出,然后找出规律,得出结论.

图6

解：(1)如图6,作直线AC和EH,两直线的交点为路灯灯泡所在的位置G,直线GC是形成影子BC的光线.(2)由题意得△ABC～△GHC,所以即解得GH=4.8(m).即路灯灯泡距离地面的高度GH为4.8m.(3)连接GA1,并延长交BC所在直线于C1,因为△A1B1C1～△GHC1,所以则解得,同理可得解得B2C2=1(m),同 理可得….探究规律：由此可得

点评本题是把实际问题抽象到相似三角形中，利用相似三角形对应边成比例的性质解题，本题也是将相似三角形性质的运用与找规律相结合的一道题，解题时要注意从特殊到一般，仔细观察，认真探求规律.

四、与方程携手求灯高

例3如图7,花丛中有一路灯杆AB,在灯光下,小明在D点处的影长DE=3 米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5 米.如果小明的身高为1.7 米,求路灯杆AB的高度(精确到0.1 米).

图7

分析在本题中,小明的身高(CD、FG)与灯高AB的比值是固定不变的,即,利用△ECD～△EAB 和△HFG～△HAB 及上面的“中间比”,代换出;再利用方程可求BD的长,进而求出AB的长.

解：因为∠CDE=∠ABE=90°,∠CED=∠AEB,所以△ECD～△EAB,所以同理得又因为CD=FG,所以.设BD=x,则BE=3 +x,BH=10 +x,所以,解得x=7.5.把BD=7.5 代入中得解得AB=5.95≈6.答：路灯AB 的高约为6 米.

点评解这道题关键是将实际问题转化为数学问题,只要把实际问题抽象到相似三角形中,利用相似比建立方程即可求解.

五、与圆相融求面积

例5如图8,在一间黑屋里用一只白炽灯照射一个球.

(1)球在地面上的阴影是什么形状？

(2)当把白炽灯向上移时,阴影的大小会怎样变化？

图8

(3)若白炽灯到球心距离为1 米,到地面的距离是3 米,球的半径是0.2 米,求球在地面上阴影的面积是多少？

分析(1)球在灯光的正下方,所以阴影是圆形;

(2)根据中心投影的特点可知：在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以白炽灯向上移时,阴影会逐渐变小;

(3)应先根据题意画出示意图,再由直角三角形、圆的切线的性质以及相似三角形的知识求出影子的半径,从而求出其面积.

图9

解：(1)影子是圆;(2)阴影会逐渐变小;(3)如图9,设点O为灯泡,点E为球心,过O作球两侧的切线,点A、B分别为切点,OA、OB分别交地面于C、D两点,连接AB、CD,则CD为球在地面上影子的直径.连接OE并延长与CD交于点F,则OF⊥CD,OE=1m,OF=3m.连接AE,因为OC切圆的半径EA于点A,所以AE⊥OC,且AE=0.2m.在Rt△OAE 中,因为∠OAE=∠OFC=90°,∠AOE=∠FOC(公共角),所以△OAE～△OFC,所以解得所以即球在地面上的影子的面积是

点评本题综合考查了中心投影的特点和规律、直角三角形以及圆的切线性质的运用.解题的关键是利用相似三角形的对应边的比相等,求出所需要的阴影的半径,从而求出其面积.