以“退”为“进” 步步为“赢”——对2019年济南市中考数学第26题的探究

山东省济南槐荫中学 (邮编：250118)

华罗庚先生说过：“退到最原始而不失去重要性的地方，把简单的、特殊的问题搞清楚了，并从这些简单问题的解决中，或者获得解题思路，或者提示解题方向，或者发现一般问题的结论，或者得到化归为简单问题的途经，从而再进到一般性问题上来”.“最原始而不失去重要性的地方”，无非是指最基本的公式、定理、数学模型、常用方法、已知结论等.尤其是面对图形复杂、直观感觉难度很大的几何探究题无从下手时，采取“退”的策略，方能达到“进”的目的.本文以2019济南中考数学第26题为例加以阐述.

1 真题呈现

小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.

1.1 猜测探究

在△ABC中，AB=AC，M是平面内任意一点，将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度，得到线段AN，连接NB.

图1

(1)如图1，若M是线段BC上的任意一点，请直接写出∠NAB与∠MAC的数量关系是，NB与MC的数量关系是；

图2

(2)如图2，点E是AB延长线上一点，若M是∠CBE内部射线BD上任意一点，连接MC，(1)中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由.

1.2 拓展应用

图3

(3)如图3，在△A1B1C1中，A1B1=8，∠A1B1C1=60°，∠B1A1C1=75°，P是B1C1上的任意一点，连接A1P，将A1P绕点A1按顺时针方向旋转75°，得到线段A1Q，连接B1Q.求线段B1Q长度的最小值.

分析该题将几何图形与动态变换相结合，考查了等腰三角形、三角形相似(全等)、图形旋转、线段最值等初中数学核心知识.问题的探究经历了从特殊到一般、再从一般到特殊的过程；问题解决过程中体现了类比、转化、特殊与一般等数学思想方法.全面考查了学生的图形识别能力、问题探究能力、逻辑推理能力等.

2 解题思路

2.1 老生常谈“手拉手”、旋转相似必成对

图4

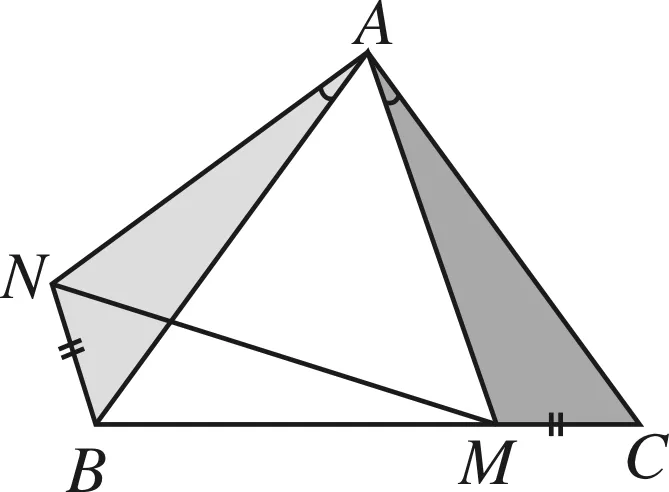
图5

对于第(1)问，如图4，连接MN，虽然点M在BC边上运动，但由题意可知△AMN始终是大小改变但形状不变的等腰三角形，又因为△ABC也是等腰三角形，这就“退”回到老生常谈的“等腰三角形‘手拉手’模型”.其常用结论为：△ABC∽△ANM；△ABN≌△ACM(旋转相似必成对，如图4、图5)，于是该问得到解决；

分析该问中，“手拉手”基本模型的出现，使问题切入点低，有章可循.该问考查了学生识别基本图形，运用基础知识与基本技能解决问题的能力.

2.2 等腰不变方法同、“退”一小步见分晓

图6

图7

对于第(2)问，与第(1)问相比动点M的位置发生了变化，由“在线段上运动”变为“在二维空间内运动”，这是“由特殊到一般”的过程.但无论点M如何运动，“△AMN是大小改变但形状不变的等腰三角形”这个事实始终没变，于是可以“退”到第(1)问的分析思路得到结论：△ABC与△ANM依然能够构成“等腰三角形‘手拉手’模型”，依然有“△ABC∽△ANM和△ABN≌△ACM”的结论，如图6、图7，所以(1)中结论仍然成立；

分析第(2)问与第(1)问相比，基本方法不变，意在考查学生用类比思想研究问题能力.该问图形稍变复杂有可能会使学生思路受阻，考查了学生的在复杂图形中识别基本模型的能力与逻辑推理能力；

通过(1)(2)问的解决我们获得的“经验”是：两个形状相同的等腰三角形，顶角顶点重合会构造出一对全等三角形.这是“手拉手”基本模型的特征，也是解答该题的“规律”；

不过第(2)问留了一个“悬念”：为什么要指明“点M是∠CBE内部射线BD上任意一点”？若“点M是∠ABC内部任意一点”或者“点M是平面内异于点C的任意一点”结论不应该都成立吗？这个“悬念”其实为第(3)问的解决埋下了伏笔.

2.3 巧破“悬念”方法找、“截长”“补短”法相通

对于第(3)问，通过审题发现，与前两问相比，旋转的方式没有变，A1P依然绕点A1按顺时针方向旋转与∠B1A1C1相等的度数，即△A1PQ依然是等腰三角形；但背景△A1B1C1的形状发生了变化，不再是等腰三角形，而是含有60°和45°特殊角的三角形.此时再“退”回到前两问，前两问的背景均为“等腰三角形‘手拉手’模型”，若能通过条件“构造”出该模型，则可延续前两问的解题思路.目前“显性”等腰三角形只有一个，即△A1PQ，怎么才能“构造”出第二个等腰三角形呢？方法有两个，“截长”或“补短”！

2.3.1 “截长”法构造等腰三角形求解

图8

图9

2.3.2 “补短”法构造等腰三角形求解

图10

分析该问通过“截长”、“补短”两种方法构造等腰三角形，从而构造“手拉手”模型，出现一对全等三角形.“截长”法应用“全等三角形对应边相等”实现线段转化，类比前面的思路，体现了转化思想；“补短”法应用“全等三角形对应角相等”通过角不变证明动点的“直线型运动路径”，运用“垂线段最短”解决问题.这两种方法均体现了模型构造的妙用；其实2.3.2的方法也可这样理解：由题意可知，点Q是由点P绕点A1按顺时针方向旋转75°得到，即每个点P对应一个点Q.因为P是B1C1上的任意一点，所以点P的运动路径是线段B1C1，于是点Q的运动路径也是一条线段，该线段由线段B1C1绕点A1按顺时针方向旋转75°得到.由“两点确定一条直线”可知，我们只需在线段B1C1上任取两点，将其分别绕点A1按顺时针方向旋转75°便可确定点Q的运动路径.为简便起见我们锁定线段B1C1的两个端点B1和C1，如图11，旋转之后的对应点分别为B′、C′，连接B′C′，线段B′C′即为点Q的运动路径.此时作B1M⊥B′Q于点M，则B1M即为B1Q的最小值.

图11

3 解后反思

3.1 以“退”为“进”、练就“慧眼识珠”

回顾本题的解决过程，第(1)问是动点在线段上运动，第(2)问是动点在二维空间内运动，这是“由特殊到一般”的过程，一般问题“退”到特殊模型方能找到问题突破口；第(3)问求动点运动过程中线段的最小值，这是“由一般到特殊”的过程，特殊结论要“退”到一般方法方能寻找.从这种意义上讲，“退”即为“进”；

如果把“手拉手”模型的应用分三个层次，第一层次应该是能证明其结论；第二层次则是能识别模型并应用其结论；第三层次则是能利用现有条件构造模型，这是模型应用的最高境界.该题前两问是对第一、二层次的考查，通过前两问我们探寻到了解决问题的一般“规律”，即利用“手拉手”基本模型解决；第(3)问则考查了模型的构造，将前两问已有的结果进行应用并推广.解决问题过程中，体现着学生知识掌握的广度与深度，练就“慧眼”，方能“识珠”.

3.2 注重联系、方能“步步为‘赢’”

在数学教学中，要关注知识间的前后联系，借助有效类比、适时转化把知识关联起来，使其系统化，增强教学的整体性；帮助学生建构良好的认知结构，并逐步内化为解决问题的能力[1].在一系列图形变化中，学生体会到“特殊与一般”、“类比”等方法的具体操作和应用，感受到解题思路的探索历程，既完善了知识体系，也发现了数学独有的变化之美[1]；

当一个题目设置多个问题时，尤其是看似复杂的几何探究性问题，问题之间往往是前后联系、相辅相成的，当然这种关联需要有扎实的数学基本功和良好的观察意识才能发现，从而可以利用前面已经求出的结果或者已经证明的结论求解后面的问题，实现“步步为‘赢’”！