北师大版高中数学必修2教材中例题解答对学生的误导分析
——以2019年高考数学全国卷I理科第18题(1)为例
安徽省淮北市第一中学 (邮编:235000)
1 问题提出
一年一度的高考在紧张的氛围中落下了帷幕,2019年的高考题也随之解开了神秘的面纱.2019年的高考卷在能力立意上有了新的高度,在核心素养的考查上有了更明确的要求,让会思考、善于动脑筋的同学得到了很好地展示,让那些死学硬背、机械记忆不求甚解的学生受到了很大的打击.
我们在关注试卷创新的同时,更应该注意到对基础知识和基本技能的考查,学生普遍反映概率题难度大做不出来,常规题型是不是都做得很好呢?为此,在高考结束后,我及时的整理了全套试卷,对高二年级的学生进行了测试(我校高二年级现已经完成了整个高中阶段的新课内容的学习,本次参加测试人数737人).
通过测试发现三角函数与解三角形、立体几何等常规题型做得也不尽如人意,特别是立体几何证明问题,学生在说理上思路不清晰,说理不充分,说理步骤不规范等导致扣分现象严重.逻辑推理能力作为六大核心素养之一,是学生获取数学结论.构建数学知识体系的重要思维方式.因此在高中数学教学中,应借助立体几何来锻炼好学生逻辑推理的严谨性和说理的充分性.
为了更好的培养学生的逻辑推理能力,我整理了本题常见的错误类型,并从学生、教材以及教学方面进行了针对性的分析,查找原因,以期能以本题为点来带动学生对整个空间几何中逻辑推理问题有更深入的认识,也为后面的复习提供可借鉴的方法和思路.
2 真题再现

图1
(2019年高考理科数学全国卷I第18题)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E、M、N分别是BC、BB1、A1D的中点.
(1)证明:MN∥平面C1DE;(2)略
参考答案:(1)连接B1C、ME,因为M、E分别为BB1、BC的中点,故ME又因为N为A1D的中点,所以
由ABCD-A1B1C1D1为直四棱柱,知A1B1AB,DCAB,故A1B1DC,则四边形A1B1CD为平行四边形,故B1CA1D,所以MEND,因此四边形MNDE为平行四边形,得MN∥ED,又MN⊄平面C1DE,ED⊆平面C1DE,故MN∥平面C1DE.
3 典型错误与分析
第(1)问分数设置为6分,参加考试的737名学生第(1)问整体平均得分3.52分,其中得6分学生有156人,占21.17%;得4—5分学生有203人,占27.54%;得2—3分学生有258人,占35%;得0—1分学生有120人,占16.28%.
面对第(1)问这样的得分情况,我心中很是担忧,也感受到了一轮复习担子之重.一个简单的直线与平面平行的证明问题,按理说不应该出现这么大面积的错误和如此低的得分情况.为此我系统的整理了得分在0—4分之间学生的答题情况,并进行了分析,对常见的错误类型进行了整理和归类,通过整理和分析发现学生错误的原因主要是思路不清晰、说理不充分、步骤不规范等,下面略选几例典型错误加以分析.
典型错误1 连接AN,通过证明平面AMN∥平面C1DE,来证明MN∥平面C1DE.
典型错误2 过点N作平面ABCD的垂线,交直线AD于P点,连接PB,则NP又MB故MBNP,所以MN∥PB,又PB∥DE,故MN∥ED,则MN∥平面C1DE.
典型错误3 连接ME,由ABCD-A1B1C1D1为直四棱柱,可得MN∥DE,又MN⊄平面C1DE,ED⊆平面C1DE,故MN∥平面C1DE.
典型错误4 连接B1C,ME,由ABCD-A1B1C1D1为直四棱柱,可得B1CA1D,又因为N为A1D的中点,所以分别为BB1、BC的中点,故ME故MEND,因此四边形MNDE为平行四边形,得MN∥ED,故MN∥平面C1DE.
对于典型错误1 是一类对证明模糊,不理解几何证明的本质,而且对空间中的几何关系判断不准确,空间观察能力不足导致的错误.对于这类学生,应强化空间图形基本关系的认识,加强学生的动手能力,通过实物观察、模型操作、动手画图来培养他们的空间观察能力和空间想象能力.
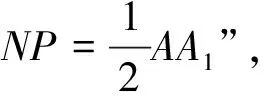
对于典型错误3和典型错误4,说理不严谨,推理过程太随意.说理上没有明确逻辑推理的基础在哪里?应该从哪里开始说理?推理证明的逻辑起点在哪?
比如典型错误3 由“ABCD-A1B1C1D1为直四棱柱”能不能得到“MN∥DE”?对于典型错误4 由“ABCD-A1B1C1D1为直四棱柱”能不能得到“B1CA1D”?四棱柱有这样的性质吗?直接由“MN∥ED”得“故MN∥平面C1DE”是不是缺少必要的直线在面内“ED⊆平面C1DE”,直线在面外“MN⊄平面C1DE”的说明?
书本上对棱柱的定义是“两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫做棱柱”“我们把侧棱垂直于底面的棱柱叫做直棱柱”.由此可以看出直棱柱有以下性质:①棱柱的侧棱互相平行;②棱柱的上下底面互相平行;③直棱柱的侧棱垂直于上下底面等.我们从书本的定义中不能直接得到诸如“MN∥DE”“B1CA1D”这样的结论啊!这种说理很大程度上取决于学生的主观臆断,看图是什么就说成什么,而没有形成很好的逻辑推理能力,不知道题目给出的信息隐含哪些已知条件,应该从何处入手进行逻辑证明?
对于典型错误3和典型错误4 犯错人数约402人占54.55%.在试卷讲评课上,我通过让学生自己分析做题思路,并讲述做题过程,然后全班同学分小组讨论集思广益,并给出不同的证明方法,来培养学生的逻辑推理能力.但是通过小组合作讨论,发现学生对于典型错误4仍然不能自主得出错误的原因.课下我找了部分同学谈谈他们对典型错误4的看法,学生给出的答案也是莫衷一是,其中有位同学说“书本上的证明就是这样说的呀!”
于是,我又翻阅了书本(北京师范大学出版社普通高中课程标准实验教科书 数学2 必修),当我细细研究书本的时候,发现了书本上的例题在逻辑推理上确实也存在着和学生一样的问题.
4 追根溯源回归课本
《北京师范大学出版社普通高中课程标准实验教科书 数学2 必修》(2014年7月第7版)(以下简称北师大版)第31面例题3题目及证明的步骤选摘如下

图2
例3 已知正方体ABCD-A1B1C1D1,求证:平面AB1D1∥平面C1BD.
证明如图2所示,ABCD-A1B1C1D1是正方体,所以BD∥B1D1.
又B1D1平面AB1D1,从而BD∥平面AB1D1.
同理可证BC1∥平面AB1D1.
又直线BD与直线BC1交于点B,因此平面C1BD∥平面AB1D1.
对于上述证明过程我们有如下的几点疑问:
(1)由“ABCD-A1B1C1D1是正方体”能不能直接得到面对角线平行,即“所以BD∥B1D1”?
(2)由“B1D1∥BD,又B1D1平面AB1D1”从而得“BD∥平面AB1D1”,是否缺少“BD平面AB1D1”的条件?
(3)由“BD∥平面AB1D1,同理BC1∥平面AB1D1,又直线BD与直线BC1交于点B”得到“平面C1BD∥平面AB1D1”,是否缺少“BD平面C1BD,BC1平面C1BD”的条件?
为此,我又翻阅了《人民教育出版社普通高中课程标准实验教科书数学2必修》(2007年2月第3版,2015年5月安徽第17次印刷)(以下简称人教A版)的相关内容,这两个版本的教材都不约而同的选择了这个题目作为例题来讲述平行关系的判定方法.现将人教A版第57面例题2题目及证明的步骤选摘如下:

图3
例2 已知正方体ABCD-A1B1C1D1(图3),求证:平面AB1D1∥平面C1BD.
证明如图2所示,ABCD-A1B1C1D1是正方体,所以D1C1∥A1B1,D1C1=A1B1.
又AB∥A1B1,AB=A1B1,
所以D1C1∥AB,D1C1=AB,
所以D1C1BA为平行四边形.
所以D1A∥C1B.
又D1A⊄平面C1BD,C1B⊂平面C1BD,
由直线与平面平行的判定定理得D1A∥C1BD,
同理D1B1∥平面C1BD,
又D1A∩D1B1=D1,
所以平面AB1D1∥平面C1BD.
通过比较可以发现:
(1)对于面对角线平行,即“D1A∥C1B”的证明,人教A版就没有像北师大版教材那么“简略”而是详细说明了由“ABCD-A1B1C1D1是正方体”得到“D1A∥C1B”的原因,人教A版教材在这个证明的过程中就很好地利用了正方体的性质,从已知条件出发来证明“D1A∥C1B”,减少了很多主观随意的成分.并且很好地体现了解决空间几何问题的基本思想——降维转化的思想.将空间正方体中的“D1A∥C1B”问题有效地转化为正方体的表面ABB1A1及A1B1C1D1中(平面中)的平行问题来处理.我们认为这也是空间几何证明问题的逻辑起点,即初中所学的平面几何中的各种线面关系,它们都可以作为立体几何中已知的结论来证明立体几何问题,但是空间几何体中除了空间几何体性质之外的点、线、面位置关系都应该进行逻辑证明,不可以凭主观判断来得到.
(2)人教A版在判定直线D1A与平面C1BD平行的时候说明了三个条件:①D1A∥C1B;②D1A⊄平面C1BD;③C1B⊂平面C1BD.这对于学生学习和掌握直线与平面平行的判定定理有很大的好处,毕竟书本上特别强调“三个条件缺一不可”,在本例题之前学生刚刚学习了直线与平面平行的判定,在紧跟的例题中应该把这种“三个条件缺一不可”体现出来.可能有人会说“表示直线C1B的两个点都在表示平面C1BD的点里面,因此这一条可以省略”,这种说法也是可以的,但是我们要注意到本节内容《平行关系的判定》是学生学习空间几何后,开始严格逻辑证明的起始课,如果在书写的步骤规范上就省略的话,学生很容易犯文章开始那样的大面积错误——说理太随意、主观因素太多、说理步骤不规范不完整,甚至说理不充分.
(3)人教A版在判定平面AB1D1∥平面C1BD时,也没有说明“D1A⊂平面AB1D1,D1B1⊂平面AB1D1”,我们认为这点应该补充一下,理由同上(2)的解释,对于平面与平面平行的判定定理“五个条件一个结论”的认识有很好的强化作用,对规范学生答题也有很好的示范作用.
5 结束语
我们认为,教材作为学生模仿的对象,应该在各个方面都起到示范作用.不应该出现让学生误导的的内容和不规范的答题步骤.
再如,北师大版教材在用符号语言表述平面与平面平行的判定定理时是如下表述的“若直线a平面β,直线b平面β,a平面α、bα,a∩b=A,并且a∥β,b∥β,则α∥β”对于上面的语言表述我们有下列疑问:①前面说“直线a”“直线b”“平面α”“平面β”,后面又直接说“a、b、α、β”,这是为什么呢?②“直线a平面β,直线b平面β”这两一条件真的需要说明吗?这种语言表述是不是有啰嗦和不规范的嫌疑呢?
我们建议,平面与平面的平行判定定理的符号语言可以这样来表述:a、b是两条不同的直线,α、β是两个不同的平面,“aα,bα,a∩b=A,a∥β,b∥β⟹α∥β”.
在平时的教学中,教师要充分理解课标,也要有自己的主见,以教材为纲不等于唯教材论,要深层挖掘教材,创造性的使用教材.对教材存在的问题要敢于提出质疑,只有这样不断的反思,才能够让学生有更大的收获.教学中要精选例题,要关注经典模型(正方体、长方体、四面体等)在教学中的作用,注重答题规范,给学生起好带头示范作用,只有这样才能使学生在答题过程中有正确的模仿对象,进而减少说理的随意性和不充分性.
由于教材编写者的逻辑语言缺乏规范性,进而给了学生一个错误的示范和导向.笔者写此文,以期引起教材编写者的注意,在教材的语言表述上要精雕细琢,慎之又慎.
说明北师大版教材和人教A版教材在直线与平面位置关系的符号表示上略有区别,直线l在平面α内,北师大版表示为“lα”,人教A版表示为“l⊂α”;直线l不在平面α内,北师大版表示为“lα”,人教A版表示为“l⊄α”,本文在引用这两本教材时不加改变地分别保留了它们各自的表示方式.

