激活知识串讲方法提升素养——对一道高三模拟题的多解与教学思考

江苏省太仓高级中学 (邮编：215411)

安徽省马鞍山市第二中学 卢建军 (邮编：243000)

近日，笔者对一道市级高三模拟考试题展开解法探究与教学思考，以期对高三习题教学有所启发．

试题(2019年马鞍山市高三模拟考理科第16题)在△ABC中，∠BAC=60°，点D在线段BC上，且BC=3BD，AD=2，则△ABC面积的最大值为．

这是一个三角形面积的最值问题，试题平和朴实、内涵深刻，给人以“题在书外，根在书内”的感觉，并自然地将等与不等、消元思想、数形结合思想等融为一体，考查学生综合运用解三角形的相关知识和方法，以及平面向量、不等式、平面几何的相关知识和分析问题、解决问题的能力，较好地检测考生的数学素养与学习潜能．

1 解法探究

图1

①

②

评析该解法属解三角形问题的通性通法，激活余弦定理和基本不等式的相关知识，教学中关键要引导学生“由已知看可知，再由未知看需知”．针对多变量代数式的处理体现了消元的思想，解法自然，学生易于想到.最后关注取等条件，同时激活了角平分线定理等知识．

9AD2=4AB2+AC2+4AB·ACcos60°≥4AB·AC+2AB·AC，即6AB·AC≤36，即bc≤6. 下同解法一．

由2S△ABD=S△ACD可得，

③

④

解析该解法激活了三角函数的相关知识，用角α来表示边b,c，最终将面积表示成关于α的三角函数式，进而求出最值，体现了利用函数思想求最值.

解法四由斯特瓦尔特定理可知，AB2·CD+AC2·BD-AD2·BC=BC·CD·BD，

解析该解法激活了平面几何等相关知识，其本质同解法一，只不过建立三边关系式的途径不同而已.

图2

解析从本质上看解三角形也是平面几何的知识，我们知道像这一类动态三角形的问题都有着几何背景，通过平面几何知识将该问题转化为一个基本问题：已知三角形中的一边及其对角，求面积的最大值. 巧用外接圆，妙解三角形. 体现了化归与转化的思想，让学生感受到任何一道难题都可以转化为我们曾经熟悉的问题．

2 问题推广

对试题进行一般化的推广探究，是学习解题的重要法宝之一.通过一般化探究，去除问题中非本质属性，执问题的牛耳.

当且仅当AD为∠BAC(或其外角)平分线时取得最大值．

图3

当λ<0或λ>1时，

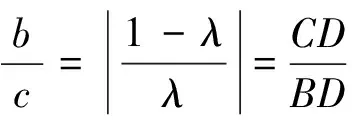
3 变式训练

题1 (2014年高考全国1卷理科第16题)已知a、b、c分别为△ABC的三个内角A、B、C的对边，a=2，且(2+b)(sinA-sinB)=(c-b)sinC，则△ABC面积的最大值为.

题2 (2018年高考江苏卷第13题)在△ABC中，角A、B、C所对的边分别为a、b、c，∠ABC=120°，∠ABC的平分线交AC与点D，且BD=1，则4a+c的最小值为．

题3 在△ABC中，∠BAC=30°，点D在线段BC上，且BC=3CD，BC=3，则AD的最大值为．

题4 在△ABC中，角A、B、C所对的边分别为a、b、c，若a2+2b2+3c2=1，求△ABC面积的最大值.

4 教学思考

上述三点可以看作是习题教学中教师备课的内容，从典型例题的选择，到解法的探究与推广，再到后期提供给学生的变式训练，经历了“选题——讲题——练题”三步曲．

作为教师，我们在试题研究中做到以上几点，对锤炼自身内功是大有裨益的，而且唯有课前深入备课，方能课中精彩演绎．一题多解就是在挖掘每个数学问题的“营养价值”，不能“入宝山而空返”，看似在讲解一道题，殊不知以及丰富联想、激活串讲了多个知识点，如此达到“以少胜多”、“举一反三”、“融会贯通”的功效，学生的能力素养在潜移默化中得到提升．

我们也经常听到这样的质疑声：课堂上如果这样玩一题多解，会不会耽误教学进度，有的解法需要教给学生吗，需要给学生讲授一般化推广吗？这些思考与质疑不无道理，如果我们抛开学生，孤芳自赏，展示解法，那就好比“一个壮汉在秀肌肉”，其教学效果可见一斑．但我们也不能“因噎废食”，诚然，不是所有的题目都适合一题多解，也不是所有学生都适合一题多解，最根本的是要因材施教，以学定教，多关注学生的表现和感受，讲解习题时做到“关注学情、充满激情”．

不同学生，不同时期，我们所教的知识侧重点应有所区别，尤其在高三后期的习题教学中，学生在已经掌握通性通法的阶段，我们要尽可能多地传递解题思路、渗透思想方法、揭示问题本质．让我们的课堂“少一点套路，多一些理性”，让我们的学生拥有更多的问题视角，突破思维定势，从容自如地应对各种新问题，成为一个善于思考、独具个性的学习者，而不是知识的容器，这就是教育成功的最大收获．