圆锥曲线弦的一个“两定”命题——由皖江名校联考试题引发的深入探究

安徽省蚌埠第三中学 (邮编：233000)

1 试题呈现及分析

已知P是圆F1:(x+1)2+y2=16上任意一点，F2(1,0)，线段PF2的垂直平分线与半径PF1交于点Q，当点P在圆F1上运动时，记点Q的轨迹为曲线C.

(Ⅰ)求曲线C的方程；

(Ⅱ)记曲线C与x轴交于A、B两点，M是直线x=1上任意一点，直线MA、MB与曲线C的另一个交点分别为D、E，求证：直线DE过定点H(4,0).

此题是皖江名校2019届高三5月联考理科试题，考查圆锥曲线方程和直线过定点问题.试题表述简洁，问题设计层次分明，难易梯度合理，内涵丰富.第(Ⅰ)问属于封闭性问题，考查单圆法生成椭圆图形，强调椭圆定义和基本方法的运用；第(Ⅱ)问体现探究问题特征，强化探究运算思路，选择运算方法，彰显数学运算与逻辑推理.对于本题的第(Ⅱ)问，笔者进一步深入的探究，得到圆锥曲线一条弦过定点的更一般性命题.

2 探究过程

本题第(2)问是整个题目命制的亮点，对它的引申推广是探究的主要过程.笔者运用几何画板思考探究，得到以下探究命题.

2.1 纵向探究：特殊到一般的探究

探究1 试题中，已知条件中指出点所在的定直线和椭圆是具体的，若点所在的定直线及椭圆是一般性的，直线DE是否依然过定点？

证明依题意知A(-a,0)，B(a,0)，且直线MA、MB的斜率存在，设点M(m,n)，则直线

所以直线DE的直线方程为

化简整理得

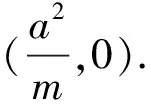
2.2 逆向探究：原命题到逆命题的探究

探究2 若椭圆上的两点D、E连线过点(m,0)，那么直线DA、EB的交点的轨迹是怎样？交点是否在定直线上？经过探究，得到如下命题.

证明由条件可得直线DE的斜率存在，设直线DE:y=k(x-m)(k≠0)，联立方程

消去y化简得(b2+a2k2)x2-2a2k2mx+a2(k2m2-b2)=0有两个不等的实根，△=4a2b2(a2k2-m2k2+b2)>0.

设D(x1,y1),E(x2,y2),M(x3,y3)，则

上两式相比得：

又结合(*)式得

第一阶段：建立一个融合标准，第一部分由所有民用要素构成，第二部分由军有民无的要素构成。这样既保证了民用要素分类与代码构成不发生变动，又包含了所有需要考虑的军用要素。

2.3 横向探究：椭圆到双曲线的探究

探究3 以上对于椭圆，那么对于双曲线，情况是怎样的？

对于双曲线有以下命题：

所以直线DE的直线方程为

化简整理得

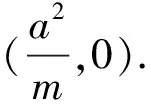
同理，双曲线也有逆命题存在，类似有以下命题：

3 背景探寻

一道试题背景的探寻，可使我们“登高望远”，抓住问题的本质，确定解题方向，寻找简捷的解题途径.

借助极点与极线知识可以深刻揭示该试题的命题思路与背景，极点与极线是高等几何中的基本概念，虽然中学数学没有介绍，但以此为背景命制的高考试题经常出现，掌握极点与极线的初步知识，才能识破题目的神秘面纱，解析试题的内在背景，并最终掌握命题规律.

以下以椭圆为例，探寻试题的内在背景.

为了问题说明的方便，给出下面引理：

引理[1]两点连线的极点是此二点极线的交点，两直线交点的极线是此二直线极点的连线.

图1

如图1，点M是直线x=m上任一点，直线AM,BM与椭圆分别交于点D、E，直线DE交x轴于点H，由极点极线的几何定义知，点M的极线为直线M′H.

下面运用同一法说明点H为直线MN的极点.

图2

极点与极线是几何中一条非常重要的性质，它在圆锥曲线问题的探究中有十分重要的应用，本文对圆锥曲线的这一“两定”问题的探究从侧面佐证了这一判断.