350 km/h高速铁路有砟轨道基床结构的技术条件分析
田地,罗强,谢宏伟
(西南交通大学 土木工程学院;高速铁路线路工程教育部重点实验室,成都 610031)
世界已经进入高铁时代,而无砟轨道凭借着高稳定性、高平顺性等特点成为中国高铁的主要结构型式,也被广泛运用于世界范围内。但有砟轨道并未就此退出历史舞台,法国高铁仍以其作为主要轨道结构型式。事实证明,有砟轨道具有满足高速列车运行的能力。相较于混凝土轨道板,有砟道床具有弹性好、维修方便、运行噪音小等特点。尤其在高寒、地震带等特殊区域,有砟轨道是一种能满足技术性及经济性的合理选择。中国正在建设世界第一条运营速度为350 km/h的有砟铁路—京张高铁,其设计经验尚属空白[1]。当前,针对高铁有砟结构的研究主要集中在轨道技术标准及飞砟治理问题,而路基基床的稳定是保证线路整体质量的前提,研究其设计技术条件是必要的,且具有现实意义。
列车运行产生的轮轨作用力传递至路基是路基基床结构设计的先决条件。轮轨作用力通常采用拟静力法得出,即以表征动力作用程度的动力影响系数φi乘以列车静荷载。各国基于不同因素的考虑选取对应的φi值,如德国综合考虑了曲线、轨道状态、运行速度、线路类型的影响[2];日本仅考虑列车速度及钢轨有无接缝的影响[3];中国学者参考研究资料,提出了列车荷载下路基面动应力经验公式,并考虑速度的影响。在轮轨作用力下,基床结构一般以强度和变形作为控制指标进行设计,如美国、法国铁路的强度控制法,即基床填料承受的动应力不大于其允许动强度;日本铁路则通过控制路基面动变形不超过2.5 mm来保障列车高速运行的安全及平稳[4]。随着列车速度的不断增加,基床承受的荷载增大、频率加快,其长期稳定性成为设计的主要考虑因素。张千里[4]提出以临界体积应变作为控制指标,以保证填料在长期荷载下不发生累积变形效应;刘晓红等[5]、周文权等[6]分别研究了红黏土以及粗粒土在长期循环荷载下的累积变形规律。综上所述,学者们对基床结构设计进行了大量研究分析,且中国现有规范也从结构受力、级配选择、压实度等方面给出了相应分析及标准。但应对今后更高速度的铁路线建设,仍存在部分问题急需解决,例如,φi的选取未能体现车辆与轨道间相互作用及轨道结构型式的影响;设计采用的单轮载作用模式不能反映路基中存在的荷载叠加效应;基床结构设计指标多以半理论、半经验公式为支撑,造成技术条件标准单一化,经济性欠佳。
基于上述问题,针对350 km/h高铁有砟轨道,建立车辆-轨道-路基垂向动力学模型;采用德国低干扰轨道谱进行仿真计算,分析列车不同速度下的路基动力响应及φi分布特征规律;根据典型高速动车组车辆的轴间距参数特点,对比了单、双轴荷载模式下路基承受列车荷载的分布情况,明确列车荷载作用模式;讨论了循环荷载下粗粒土填料累积变形状态阈值与荷载水平的关系,并阐明了不同等级铁路路基各结构层对应累积变形状态的设计控制要求;以填料动强度、长期动力稳定性及循环变形为设计三原则,K30为主要设计参数,提出适于350 km/h有砟基床双层结构型式的技术条件标准建议。
1 路基承受列车荷载作用效应
1.1 路基承受列车动力效应类别
采用动力影响系数φi表征列车动力效应,如式(1)所示。
Pd=Ps·φi
(1)
式中:Pd为动轮载力;Ps为静轮载力。
大量研究显示,φi自钢轨沿深度不断衰减。考虑一定的安全储备且方便计算传递至路基的轮轨作用力大小,遂假定路基面以下φi保持不变,并根据基床结构不同功能需求将路基承受的列车动力效应分为两类:反映路基结构可能承受的最大动荷载pdj,对应极限动力影响系数φ1;反映路基结构长期工作中承受频率最大的常遇动荷载pdc,对应常遇动力影响系数φ2。
1.2 车辆-轨道-路基耦合动力效应
文献[7]将列车在轨道上的运动描述为各系统间相互的动力学作用过程,与轨道结构型式、车辆、轨道状态等因素有关。因此,建立车辆-轨道-路基垂向耦合动力学模型进行分析,结构简图如图1所示[8]。

图1 车辆-轨道-路基耦合动力学垂向模型Fig.1 Vertical model of vehicle-track-subgrade coupling
1)车辆参数 基于CRH380A型车,整车为以悬挂弹簧-阻尼元件连接的各质量块组成(车体-转向架-轮对)的整车两系悬挂模型,参数见表1。

表1 CRH380A型车辆参数Table 1 CRH380A vehicle parameters
2)有砟轨道-路基参数 将钢轨看作连续弹性点支承的无限长梁,轨下各结构以轨枕支点为单位沿纵向被离散。支承单元以质量元件、弹簧-阻尼元件作为反映不同部分的作用关系。通过引入剪切刚度和剪切阻尼,考虑道床内部嵌挤与剪切作用。有砟轨道及路基参数见表2。

表2 有砟轨道-路基参数Table 2 Tracks-subgrade parameters
3)轨道不平顺谱 路基动力响应主要受轨道高低不平顺影响,采用德国低干扰轨道谱的高低不平顺功率谱密度函数Sv(Ω)作为轨道不平顺系统激励,如式(2)所示。
(2)
式中:Av为粗糙度常数;Ωc、Ωr为截断频率,具体参数见表3。

表3 德国低干扰轨道谱功率谱密度函数参数Table 3 German low-interference vertical profile PSD function parameters
根据式(2)计算频谱幅值,采用MC方法生成随机相位,基于傅里叶逆变换得出对应的时域模拟样本,如图2所示。

图2 轨道高低不平顺模拟结果Fig.2 Vertical profile irregularity
采用MATLAB平台,结合上述模型仿真模拟车辆在德国低干扰高低不平顺谱下运行。当轨道长度大于100 m后,计算结果几乎不受运行距离的影响[8],因此,综合考虑计算时间及统计样本量因素,取轨道长度为160 m,除去两边各30 m的边界长度及车辆前轮与后轮轴间距约20 m后,实际模拟车辆直线运行为80 m;轨枕扣件节点134个;截取波长为0.5~200 nm;钢轨截取前333阶模态;整个系统自由度为1 675。模拟车辆以不同速度v运行,得到各扣件节点正下方路基面承受的最大动力荷载,单扣件节点传递至路基面受力面积按道床压力35°扩散计算,则路基面承受动应力如表4所示,其结果随着速度增大而增大。

表4 路基面动应力统计参数Table 4 Subgrade surface dynamic stress statistical parameters
以速度0 km/h为基准,计算不同速度v下路基承受列车荷载动力影响系数φi。v=350 km/h时,沿线路纵向的路基φi统计分布情况如图3所示。

图3 350 km/h下路基面φi统计结果Fig.3 350 km/h subgrade surfaceφi statistical
通过SPSS软件进行K-S检验,v=350 km/h时的φi服从对数正态分布,即ln(φi)~N(0.347,0.1742),K-S检验结果如表5所示。基于对列车动力效应类别的区分,取单侧(右截断)保证率50%的均值μ作为常遇动力系数,即φ2=1.41;取单侧(右截断)保证率为97%的分位值φ1=1.96作为极限动力系数。仿真计算结果更能体现不同列车速度对路基承受动力作用的影响,较现行规范单一冲击系数的规定,其结果更具经济性。

表5 K-S检验结果Table 5 K-S test results
1.3 列车荷载模式
列车荷载下路基动力效应分布特征与轴重、轴间距、轴数有关[9]。CRH380A型车转向架轴距为2.5 m,而前后车相邻轮轴轴距约6 m。因此,仅需考虑同一转向架两轮载的相互作用对路基动力响应的影响。
通常假设路基为半空间弹性体,并采用Boussinesq公式计算路基承受的列车荷载。由于路基填料为松散碎石土,变形模量差异不大,可不考虑厚度当量代换,且结果更为安全。计算时选择从轨枕底部开始,单轮载力作用于轨枕正上方时,基于Gauss函数法[9]得到5根轨枕分担的比值。多个单轮载作用效应的代数叠加即为多轮载作用效应。
将轴距由2 500 mm缩减至2 400 mm,与4倍匹配轨枕间距(600 mm)相匹配,这样方便计算,且路基面应力计算结果对于设计偏于安全,误差在2%以内[10],将此命名为“动车组2Z2400荷载模式”,如图4所示。

图4 动车组2Z2400荷载模式
由此计算350 km/h时单轴荷载模式与2Z2400荷载模式下路基承受荷载沿深度变化情况,结果如图5所示。

图5 路基承受动力效应沿深度分布Fig.5 The embankment bears dynamic effects along
计算表明,相较于单轴模式,考虑双轴叠加的2Z2400荷载模式下路基承受荷载沿深度方向明显增大。因此,采用2Z2400荷载模式计算路基荷载分布更为安全可靠。
2 粗粒土累积变形状态阈值参数
2.1 累积变形状态分类
研究表明,循环荷载下基床填料承受动荷载大于某临界动荷载时,填料累积变形逐渐累积且不收敛,直至最终破坏。为了研究高速铁路粗粒土填料的累积变形演化状态特征,刘钢等[11]进行了室内单元模型试验。试验表明,可由负幂函数拟合填料累积变形,速率v(N)与荷载作用次数N的关系式,如式(3)所示。
v(N)=C·N-λ
(3)
式中:λ为变形速率幂指数;C为常数。
逐级增加动荷载p,直至填料破坏,进而得到λ-p曲线,如图6所示(压实系数Kh=1.0)。根据负幂函数性质,以λ为指标划分粗粒土累积变形状态,即快速稳定状态(λ≥2)、缓慢稳定状态(1≤λ<2)、缓慢破坏状态(0<λ<1)、快速破坏状态(λ≤0),状态阈值分别为快速稳定荷载阈值p1(λ=2)、缓慢稳定荷载阈值p2(λ=1)、快速破坏荷载阈值p3(λ=0)。p=p3时,填料出现明显的破坏特征,即认为p3为粗粒土填料动极限承载力pd。为表征缓慢稳定状态下累积变形演化快慢,可将缓慢稳定状态等分为3种亚状态,即轻微时间效应变形状态(1.67<λ<2)、微弱时间效应变形状态(1.33<λ<1.67)、中等时间效应变形状态(1<λ<1.33),对应的荷载阈值分别为pl1(λ=1.67)和pl2(λ=1.33)。
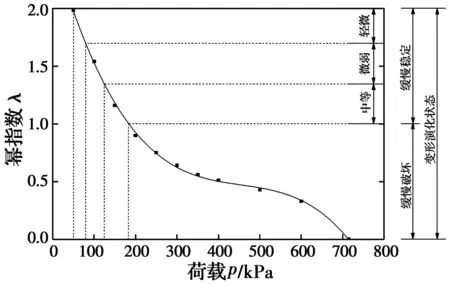
图6 粗粒土λ-p关系曲线Fig.6 Coarse soil λ-p relationship
2.2 累积变形状态与荷载水平阈值的关系
熊勇等[12]提出以荷载水平划分压实填料的累积变形状态,定义荷载水平α为施加动荷载p与动极限承载力pd的比值如式(4)所示。
α=p/pd
(4)
由文献[9]中经验式(5)和式(6)推算压实填料在模型试验实测K30=380 MPa/m时,动极限承载力p′d=2[pd]=834 kPa,模型试验测得动极限承载力p″d=715 kPa,相对误差仅为16.6%,故可取p′d与p″d的平均值作为pd的真实值,即pd=775 kPa。
[p0](kPa)=2.4K30(MPa/m)+15
(5)
[pd]=0.45[p0]
(6)
式中:[p0]为填料静允许承载力;[pd]为填料动允许承载力。
由此得到典型粗颗粒土填料荷载水平阈值分别为:快速稳定荷载水平阈值α1=6.13%、轻微时间效应荷载水平阈值αl1=10.65%、微弱时间效应荷载水平阈值αl2=16.36%、中等时间效应荷载水平阈值α2=23.70%及快速破坏荷载水平阈值α3=100%,λ-α变化关系如图7所示。

图7 粗粒土λ-α关系曲线Fig.7 Coarse soil λ-α relationship
由式(4)~式(6)及荷载水平阈值αi可得压实填料的荷载阈值pi(kPa)与K30(MPa/m)的关系,如式(7)所示。
pi=αi(2.16K30+13.5)
(7)
3 基床结构设计方法
3.1 确定基床厚度
基床实质是列车循环荷载作用下路基显著的累积变形效应区,其厚度与基床以下填料性质密切相关。熊勇等[12]认为,快速稳定状态即对应完全弹性状态,即无时间效应变形状态。因此,针对高速铁路,基床以下填料承受的pdc小于其快速稳定阈值p1,如式(8)所示。
pdc≤p1
(8)
3.2 基床结构设计准则
1)强度准则 首先,基床各结构层填料需承受列车运行时产生的动应力幅值,则填料承受的极限动荷载pdj小于其[pd],如式(9)所示。
pdj≤[pd]/K
(9)
式中:K为安全系数,参考《铁路路基极限状态设计暂行规范》[13],高速有砟铁路可取1.4。
2)长期稳定性准则 为保证基床填料在列车循环荷载作用下累积变形速率逐渐收敛,累积变形逐渐趋于稳定,且处于正常工作状态,则填料承受的pdc小于累积变形处于稳定状态所对应的荷载阈值。
基床填料控制状态的选取应符合铁路结构特点及服役要求,区别于普速铁路和无砟轨道高铁,应控制高速有砟铁路基床填料工作状态处于微弱时间效应稳定区,由式(10)检算。
pdc≤pl2
(10)
3)循环变形准则 在列车运行条件下,为保证列车平稳性,路基面不能产生过大的循环变形S,如式(11)所示。
S≤[S]
(11)
式中:[S]为动变形限制值,对于有砟轨道取1 mm[13];S由基床填料循环变形及基床以下填料循环变形构成,并假设基床填料循环变形占S的90%。
3.3 循环变形模量
1)剪切模量-剪应变的关系 Hardin-Drnevich[14]黏弹性双曲线模型能较好地描述粗粒土动应力-动应变关系,骨架曲线可采用剪切模量与剪应变的关系表示,如式(12)、式(13)所示。
G/G0=1/(1+γh)
(12)
γh=(1+ae-bγx/γΓ)γx/γΓ
(13)
式中:G为骨干曲线的割线模量;G0为初始模量;γh为修正应变;γx为循环应变;γΓ为参考应变;a、b均为由试验确定的参数。
Vucetic[15]认为,在循环荷载模式下,当土体超过临界体积应变阈值后,土骨架发生改变并发生累积变形,对大量土体试验数据分析显示,临界体积应变阈值平均对应的土体剪切模量比为0.65。对于粗粒土填料,可认为其塑性指数Ip=0,利用式(12)、式(13)对Vucetic的对应数据进行拟合,得到γΓ=357.4 με,a=0.65,b=1.05。
对于高铁有砟轨道,基床循环变形限值为1 mm,循环变形区近似取3 m,则ε1=0.033 3%。
2)K30与循环动模量的关系 基于弹性假设,K30试验的荷载p与变形s的关系曲线可用式(14)表示。
s=0.79(1-μ2)d·p/E0
(14)
式中:d为圆形承载板直径,m;μ为土的泊松比,一般取0.21;s=1.25 mm时,板底接触压力与竖向变形之比p/s即为K30值;E0为填料弹性模量。
由式(14)可得,E0与K30的关系式(15)。
E0=0.227K30
(15)
K30试验中,承载力沿深度影响区域约为2倍板径,可认为区域内填料变形限值为1.25 mm,占总变形的90%,故K30试验填料的平均压缩应变ε2约为0.187 5%。
由于二次变形模量Ev2测定的加载方式较K30试验更接近基床填料承受的循环荷载作用方式,参考德国铁路Ev2设计标准:对于基床表层Ev2/Ev1≤2.3,底层填料Ev2/Ev1≤2.5。故可以认为循环修正K30变形模量Ed0是弹性模量E0的2倍。则填料循环修正K30变形模量Ed0与K30的关系,如式(16)所示。
Ed0=2E0=0.454K30
(16)
在一维弹性变形状态下,即认为土体侧向位移为零时,土体侧压力系数K=μ/(1-μ),并认为土的泊松比μ不变,此时,按照广义胡克定律,土体内最大剪切应变与竖向压缩应变在数值上相等,即γmax=ε。
因此,基床填料在循环变形限值1 mm下的最大剪切应变γ1=333 με,K30试验下的最大剪切应变γ2=1 875 με,其对应的剪切模量比分别为0.463 1与0.159 7。基床填料在循环变形限值1 mm下的循环变形模量Ed为循环修正K30变形模量Ed0的2.9倍,如式(17)所示。
Ed=2.9Ed0=1.32K30
(17)
3.4 基床设计步骤
综上所述,基床结构设计步骤如图8所示。
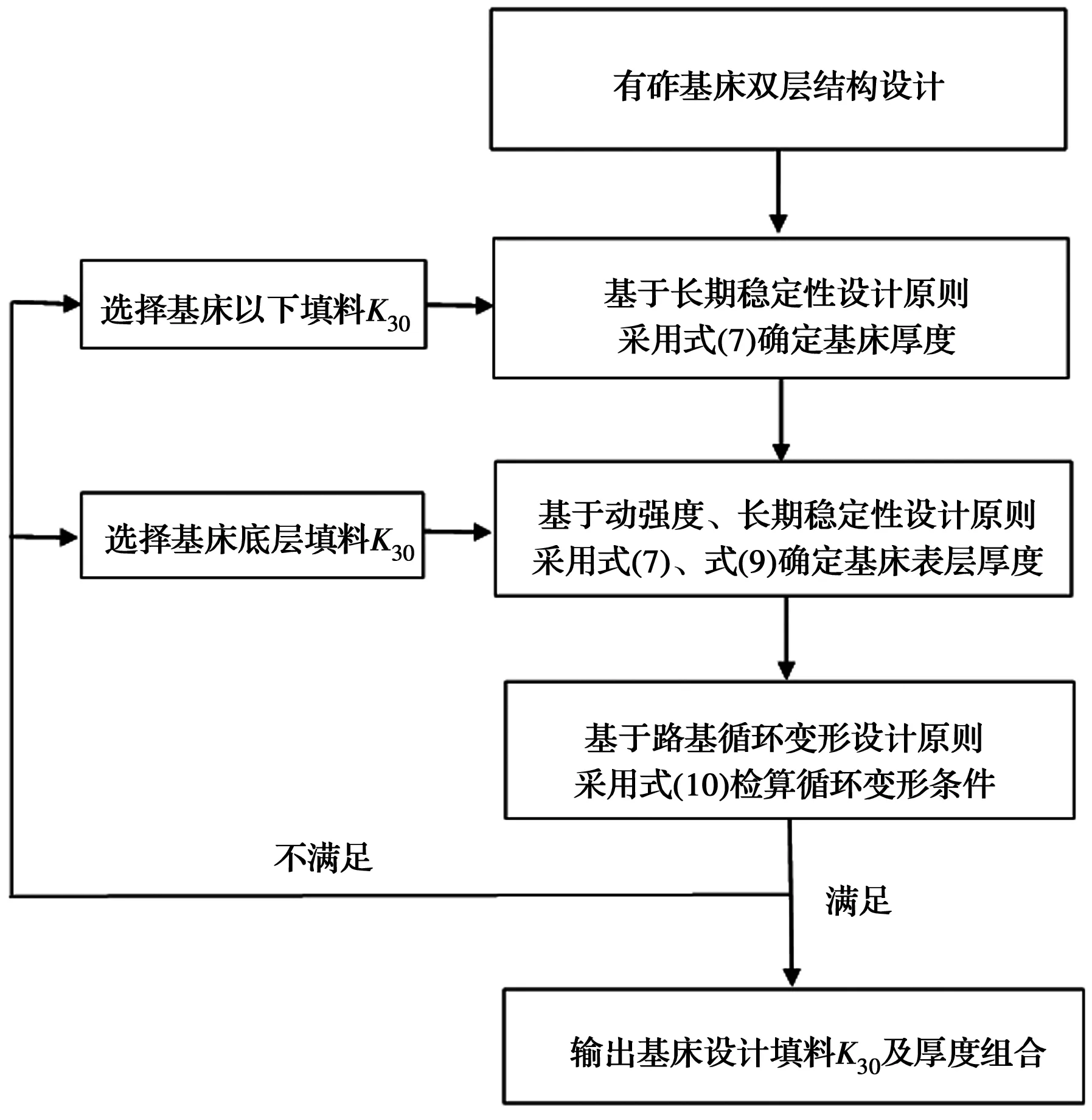
图8 基床结构设计步骤Fig.8 Subgrade structure design
4 计算示例
4.1 计算参数
采用高速铁路有砟轨道2Z2400荷载模式计算路基承担动荷载作用,如图4所示。设计速度350 km/h,动力影响系数取φ1=1.96,φ2=1.41。
采用60.64 kg/m的CHN60钢轨、长2.6 m的Ⅲ型枕;轨枕间距0.6 m,有效支承长度le=2.18 m,高弹性扣件,重0.171 kN/套;单线道床顶部宽3.6 m,容重17.5 kN/m3,碎石道床厚度0.35 m。
基床采用表层强化的双层结构,其中,级配碎石基床表层压实系数K≥0.97,K30取190 MPa/m;基床底层A、B组填料压实系数K≥0.95,K30取90~150 MPa/m;基床以下A、B、C组填料压实系数取K≥0.92,K30取70~130 MPa/m。
4.2 基床动荷载分布
列车运行时轮载正下方基床承受动荷载最大,采用Boussinesq公式计算,该截面沿深度方向路基动荷载如表6所示。

表6 不同深度下路基承受动荷载Table 6 The dynamic load of subgrade in different depths
4.3 计算结果分析
基于上述设计参数,将K30作为设计主要参数,以动强度、长期动力稳定性及循环变形为设计原则进行350 km/h有砟基床双层结构设计,结果如表7所示。

表7 基床结构设计组合Table 7 Design combination of subgrade bed
计算表明,长期稳定性始终是设计主控原则,以此保证基床以下填料处于无时间变形效应状态(λ≥2)、基床填料处于微弱时间变形效应状态(1.33≤λ≤1.67)。基床厚度与基床以下填料性质密切相关,基床以下路基填料K30由70 MPa/m提高到130 MPa/m 时,基床厚度随之由3.8 m降至2.15 m,当K30=110 MPa/m时,计算基床厚度为2.6 m。基床底层填料性质决定基床表层厚度,当基床底层填料K30在90~150 MPa/m范围变化时,基床表层厚度标准相应在0.85~0.30 m变化,K30=130 MPa/m时,基床表层厚度取0.45 m。在路基各结构层填料K30标准相同时,基床结构层设计厚度较现行规范要求更具经济性,并有一定的安全储备。
5 结论
基于车辆-轨道-路基耦合动力学原理,分析高铁有砟轨道路基面承受列车荷载的特征,以满足填料结构动强度、长期稳定性及路基面循环变形为设计原则,K30为主要设计参数,开展了350 km/h有砟高速铁路基床结构技术条件研究,得出以下结论:
1)考虑有砟轨道高低不平顺的随机影响,表征路基承受列车荷载作用的动力影响系数φki沿纵向服从正态分布规律。计算表明,列车以350 km/h运行时,ln(φi)~N(0.347,0.1742),其中,极限动力影响系数φ1=1.96和常遇动力影响系数φ2=1.41可用于反映路基服役期内承受的典型动力效应。
2)在列车荷载作用下,以保证路基产生的累积变形效应区不超过基床厚度范围为技术原则,提出基床以下路基填料的技术条件。设计计算表明,路基累积变形效应区与填料性质密切相关,基床以下填料K30≥110 MPa/m时,基床厚度为2.6 m。
3)针对高铁有砟轨道可周期性维修的技术特点,以列车荷载作用下基床填料累积变形处于微弱时间效应状态为控制目标,提出了适用于350 km/h有砟高速铁路双层基床结构的技术标准建议:基床厚度取2.6 m,基床表层采用0.45 m厚级配碎石进行强化,K30≥190 MPa/m,基床底层采用2.15 m厚A、B组填料,K30≥130 MPa/m。

