倾斜基岩条件下轨道交通振动衰减规律研究

杨金川，丁选明，瞿立明，崔春义，李铮，巫崇荣

(1.重庆大学 山城城镇建设与新技术教育部重点实验室；库区环境地质灾害防治国家地方联合工程研究中心，重庆 400045；2.大连海事大学 土木工程系，辽宁 大连 116026；3.重庆市城市建设投资(集团)有限公司，重庆 400023)

轨道列车在高架段运行时，由于轨道不平顺、车辆不圆度和列车轴重等激励下引起轨道结构振动[1]，振动通过桥梁传到桥墩，再通过桩基础传到土体中，从而引起地表振动。这些振动会造成周围建筑物沉降、结构强度降低，引起墙体开裂等问题；当人体处于振动环境中时，振动会引起头晕、精神难以集中等不适症状；当振源附近存在其他精密仪器时，仪器的正常使用将受到影响[2-3]。因此，轨道交通引起的环境振动问题不容小视。

据统计，山城重庆城市轨道交通中，高架部分占51.5%[4]，由高架列车引起的环境振动问题也越发突出。许多学者对高架轨道交通列车引起的环境振动进行了大量的研究。何鉴辞等[5]研究了列车通过高架桥直线段和曲线段时各自的衰减规律及其频谱特性；李丹等[6]基于动力学理论，获得了不同桥梁跨度、不同列车速度下产生的振动波及其在层状土体中的衰减规律；李小珍等[7]通过实测研究和理论分析得出了高架车站不同区域的环境振动规律。高广运等[8]采用半解析数值法建立高架桥线路地面振动模型,研究了桩直径、桩长、桩间距和轨道不平顺对地面振动的影响；Feng等[9]通过现场测试对比分析了高铁通过路堤、涵洞、高架和过渡段时地表振动特性。Connolly等[10]通过现场试验比较了路堑、路堤和路基面3种路基形式下轨道产生的振动水平，研究发现，路堤形式下产生的振动水平最低，路堑最高；Degrande等[11]研究了列车速度在256～314 km/h的情况下，振动强度随振源距离的分布规律，发现地面振动在距线路20～40 m的范围处存在一个反弹增大区。Kouroussis等[12]对布鲁塞尔和巴黎/伦敦之间典型场地中由HST引起的振动进行了现场测量，研究了火车特性和土壤分层对地面振动的影响。

以上研究在振动衰减规律、振动对周围环境影响和振动响应特性等方面取得许多有意义的成果，但大都是通过建立在均质的、无限大水平的土体中得到，地形对轨道交通振动衰减规律的影响研究尚少。考虑到山区地形的特殊性，轨道交通路线不可避免地穿越复杂地形，因此，研究地形对轨道交通振动衰减规律的影响具有重要意义。

本文通过模型槽试验与有限元模拟研究了倾斜基岩条件下轨道交通振动的衰减规律，并分析了基岩倾斜角度、加载频率、桩长对轨道振动衰减规律的影响。

1 模型试验

试验采用的土工模型槽系统主要包括模型槽、反力架系统、动力加载系统、测量系统4部分。模型槽尺寸长×宽×高为2.5 m×2 m×3 m，位于地表以下，上部设有反力架系统。试验所用填土为粉质砂土，天然含水率为14.01%，最大干密度为1.64 g/cm3，最小干密度为1.17 g/cm3。试验采用刚性钢板模拟倾斜基岩地层，基岩倾角β=26.6°。采用预制钢筋混凝土桩，桩长1.2 m，直径106 mm。试验使用东华测试DH5921型数据采集仪，自带64通道，数据处理采用配套的DHDAS动态信号采集分析系统，土体表面使用东华测试研制的2D001V型速度传感器。

1.1 试验方案

试验采用单桩模型，将正弦波荷载作用于桩顶，输入荷载时程函数N=2.4+0.8 sin(2π·13t)。其中，t为时间，单位为s，荷载单位为kN。目前，许多关于轨道交通的研究均以竖向振动为主[13-14]，因此，本试验采用测量竖向振动的速度传感器，下文振动测试数据均为竖向振动数据。

如图1所示，将刚性钢板倾斜放入模型槽中固定，然后填土，并分层夯实，填土高度达到70 cm时，在槽中心处放桩固定，继续分层填土夯实至180 cm，桩头露出表面10 cm以便加载。平整土体表面后，将速度传感器沿桩呈放射状布置，各方向每30 cm布置1个，其中1#测点距离桩侧8 cm，考虑距离桩侧较近的与桩同心圆上地表各处的振动响应差异很小，因此，将1#测点作为所有方向的公共测点。土体表面共布置14个速度传感器，其平面布置图与现场布置图分别如图2、图3所示。其中，传感器沿桩径向在α=0°、45°、90°、135°、180° 5个辐射方向布置；2#～6#、7#～11#、12#～14#测点分别在r=38、68、98 cm的圆上，r为距桩边的距离。

实验通过动力加载系统模拟正弦荷载，并将加载板作用于桩头，试验每次加载5 min，静置15 min后进行下一次加载。

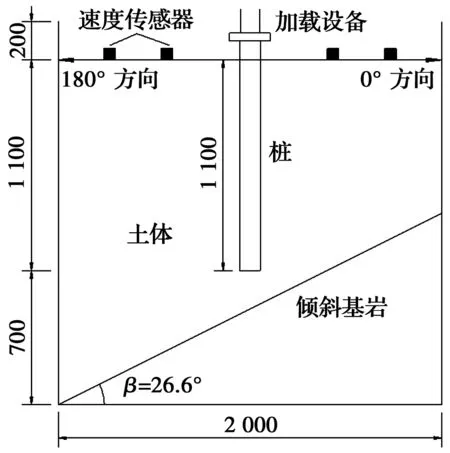
图1 模型布置剖面图Fig.1 Sectional view of the

图2 模型布置平面图Fig.2 Plan layout of the

图3 速度传感器布置现场图Fig.3 Arrangement of speed sensors in

1.2 试验结果分析

为研究倾斜基岩条件下地面振动的衰减规律，分别进行倾斜基岩和水平基岩条件下的模拟试验，并对比两者差异。测得倾斜基岩工况下地表45°方向5#、10#、14#测点振动时程曲线，如图4所示。通过傅里叶变换得到频域分析图，如图5所示。

图4 45°方向测点振动时程曲线Fig.4 Time history of measuring points in 45°

图5 45°方向测点振动频谱曲线Fig.5 Fourier’s spectrum of measuring points in 45°

图6 倾斜基岩条件下地面峰值速度衰减规律Fig.6 Attenuation of ground peak velocity for the

图7 水平基岩条件下地面峰值速度衰减规律Fig.7 Attenuation of ground peak velocity for the

图4表明，地面振动响应在一定距离范围内随着距离增加而减小；图5表明，在45°方向各测点的频谱曲线中，3个测点的频率分布一致，优势频率为13 Hz，与输入荷载频率相同，且距桩越近速度幅值越大。

图6、图7分别表示倾斜基岩与水平基岩条件下地表速度峰值衰减规律，两种工况下，振动总体衰减趋势较为一致，呈现出先快后慢的规律。在水平基岩工况下，地表振动沿各方向衰减规律大致相同；但在倾斜基岩工况下，振动沿桩径向衰减快慢则呈现明显的方向性差异，振动沿0°方向衰减最为迅速，沿180°方向衰减最慢，且从0°方向到180°方向衰减速率逐渐变小。该现象可能是由于波沿倾斜基岩面反射而向倾斜面下方聚集造成。图8为与桩边等距离处地面峰值速度变化规律，水平基岩下，在距桩边等距离各点上的速度响应较为一致，而在倾斜基岩条件下，距桩边等距离各点的峰值速度从0°到180°方向逐渐增大，且两种工况的峰值速度差从0°到180°方向呈现逐渐增大的趋势。值得注意的是，在实验中，当荷载频率较大时，荷载加载瞬间地表速度响应突然增大，根据Dowding[15]的解释，这种地面振动的增加可达到4倍，并且，当荷载频率瞬间通过产生最大地面振动的频率时就会发生。本文中所取的速度峰值均为稳态值。

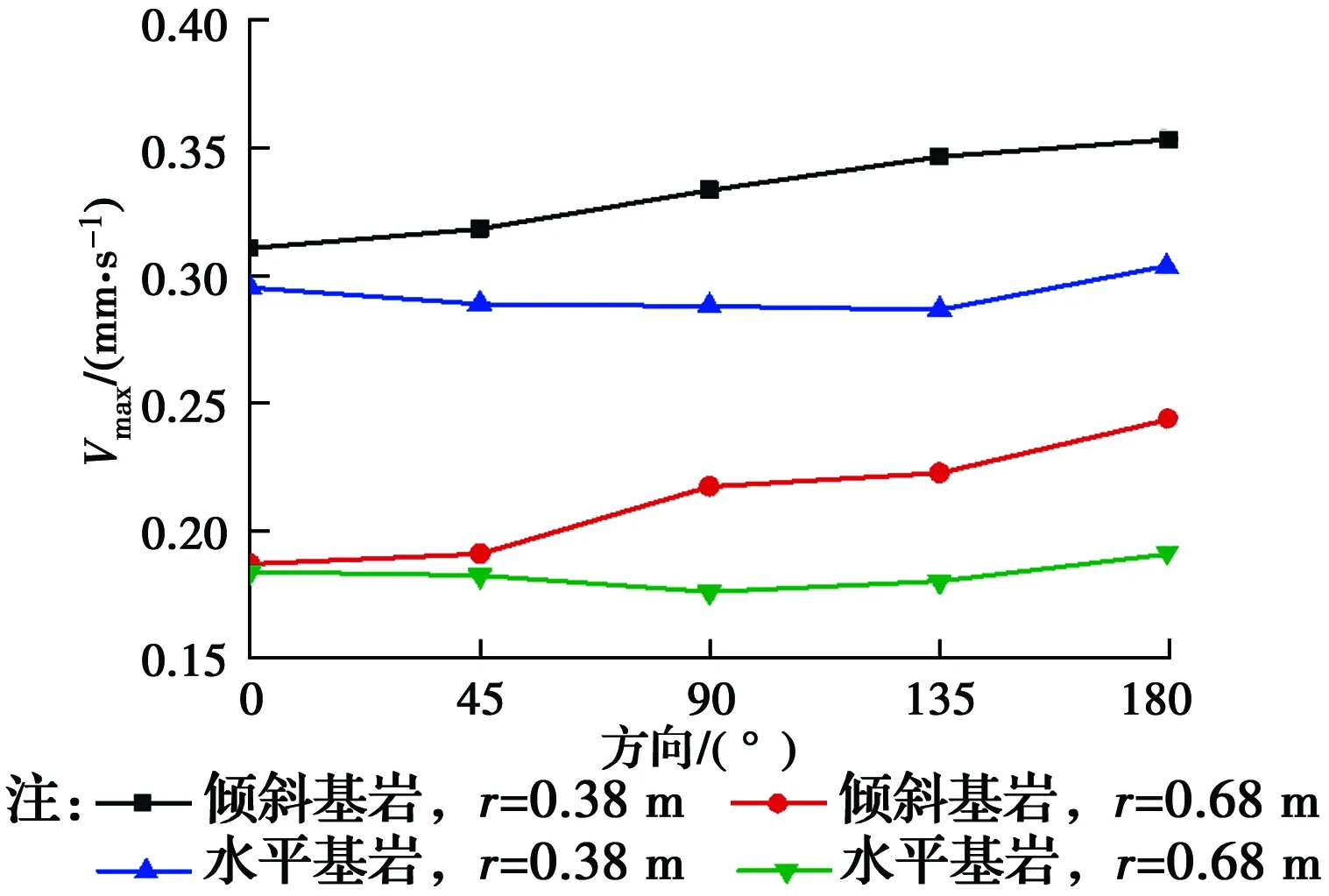
图8 与桩等距离处地面峰值速度变化规律Fig.8 Variation of ground peak velocity at different radial

2 试验数值验证

2.1 数值模型建立

采用ABAQUS有限元软件，进行三维数值模拟研究。数值模型几何尺寸与试验相同，土体水平面长×宽为2.5 m×2 m，土层最厚处为1.8 m，基岩倾斜角为26.6°，土体采用各向同性线弹性模型，模型应力应变表达式为

(1)

式中：土体弹性模量E=30 MPa，泊松比v=0.25；混凝土桩长1.2 m，直径0.106 m，弹性模量E=30 GPa，泊松比v=0.17。

在有限元动力分析中，结构阻尼通常采用表示为质量阻尼与刚度阻尼线性之和的瑞利阻尼形式，即

[C]=α1[M]+β1[K]

(2)

通常α1、β1的值采用振型阻尼比ξi计算得出。如果ωi是第i阶模态的固有频率，根据振型正交条件，α1和β1与振型阻尼比之间应满足式(3)。

(3)

在动力分析中，由于结构前几阶振型起主要作用，通常分析中根据第一振型确定阻尼，即

(4)

式中：阻尼比为0.05，模型一阶振型频率为22.09 Hz。

模型网格划分采用六面体单元，在靠近桩土接触面的位置，利用种子偏置功能进行加密，土体采用扫掠网格划分技术，模型网格如图11所示，土体四周采用固定边界，底部也采用固定边界模拟倾斜基岩。

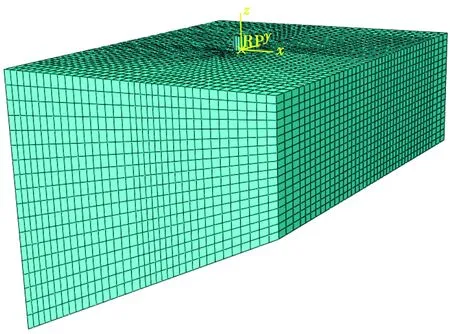
图9 三维有限元网格Fig.9 Three-dimensional finite element

2.2 试验数值验证

为验证数值模型的合理性，选取土体表面具有代表性的45°方向、135°方向数值计算结果与试验进行对比，下面分别对比了数值与试验的振动衰减曲线和时程曲线。

图10(a)、(b)表明，数值模拟结果较试验值先衰减快后衰减慢，在距桩较近测点上误差较大，其他距离处则对应得较好，数值结果的整体变化规律与试验结果较为一致，地表振动沿各方向衰减呈现方向差异化，从45°方向到135°方向衰减速度逐渐变慢；在距桩等距离的各方向上，峰值速度也从45°到135°方向逐渐增大。图10(c)、(d)分别对比了2个方向的时程曲线，数值与试验结果吻合度较好，二者时程曲线规律一致。考虑到试验误差，数值结果具有较高的可靠性。

图10 试验与数值结果对比Fig.10 Comparison of test and numerical

3 参数影响分析

前文对比了试验数值结果，验证了数值模型的合理性，下面将通过数值模型来研究基岩倾斜角度、加载频率、桩长等单一变量对地表振动衰减规律的影响，各参数取值见表1。

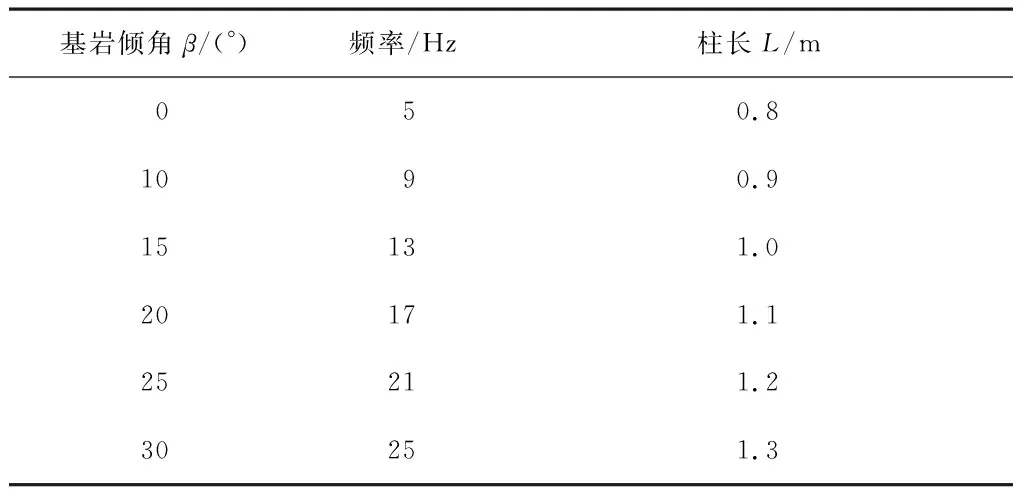
表1 各参数取值表Table 1 Parameter list

为了描述各变量对振动沿各方向衰减差异性的影响，引入归一化值N，N为与桩同心圆上各点速度响应峰值除以圆上0°方向速度峰值归一化得到，即

(5)

式中：Ri为同心圆上各点处速度峰值；R0为同心圆上0°方向速度峰值，再引入归一化值N1，表示桩径向上各点峰值速度除以桩边第1个点峰值速度归一化得到。

3.1 基岩倾斜角度的影响

为研究基岩层倾斜角度对振动衰减的影响规律，数值模拟中控制倾斜角度β在10°～30°之间变化，并与水平基岩层(β=0°)工况进行对比，输出数值计算结果如图11～图13所示。

图11 地面振动响应随基岩倾角变化规律Fig.11 Variation of ground dynamic responses withbedrock

图12 0°方向衰减曲线随基岩倾角变化Fig.12 Variation of attenuation curve with bedrock dip in direction of

图13 180°方向衰减曲线随基岩倾角变化Fig.13 Variation of attenuation curve with bedrock dip in direction of

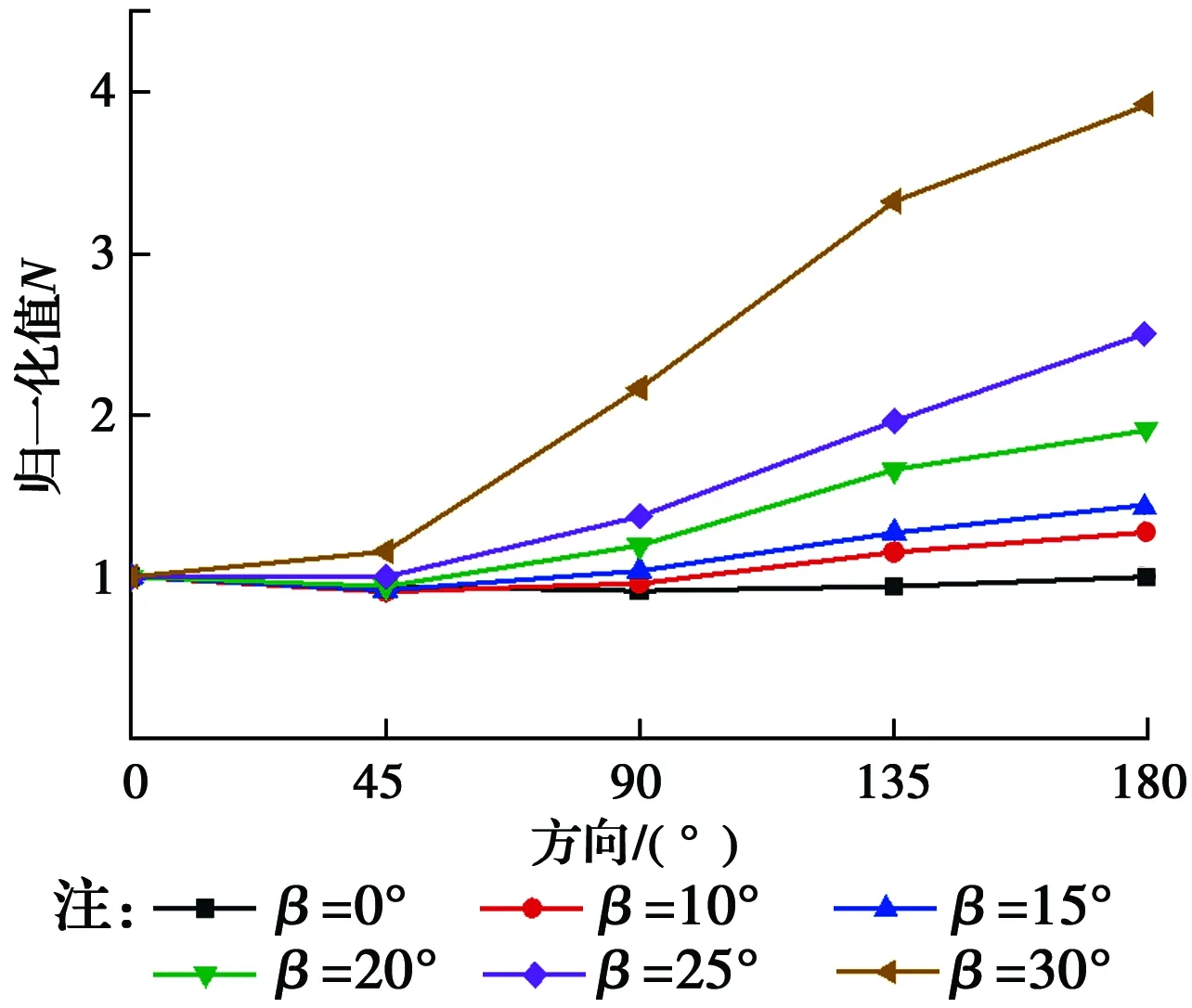
图14 r=68 cm环线上速度响应随基岩倾角变化Fig.14 Variation of velocity response with bedrock dip for the case of r=68

如图11所示，基岩倾斜角度越大，地面振动响应越小，且对各方向的影响呈现出差异化。在0°方向上，地面振动速度峰值随角度增加呈线性减小，且各距离上减小速率一致；在180°方向上，速度峰值随角度增加则是无规律减小，且减小速率明显低于0°方向。图12、图13分别表示基岩倾斜角度对0°、180°方向振动衰减的影响规律，从图中可以得出，基岩倾斜角度变化对地表振动衰减规律也呈现差异化影响。在0°方向上，随着基岩层倾斜角度增大，地面振动衰减速率逐渐增快，且随倾角呈线性增加；在180°方向上，各倾斜角度下，该方向的振动衰减曲线几乎重合，因此，该方向振动衰减规律不受基岩倾角变化的影响；在倾斜基岩的情况下，两个方向的振动衰减速度均明显快于水平基岩工况，可见倾斜地层对振动衰减的影响较为显著。图14表示地表与桩等距离处(r=68 cm)各测点振动响应差异随基岩倾角的变化规律。当基岩倾角较小时，与桩等距离圆上各方向的振动响应差异较小，且水平基岩工况下各方向振动较为一致，差异最小；随着倾角的增大，各方向的速度峰值差异显著增大。从图中看到，当倾角β=30°时，180°方向的峰值速度约为0°方向速度峰值的4倍。同时注意到，当基岩倾斜角度较小时，各方向的峰值速度最小值出现在45°方向上，随着倾斜角度的增大，最小值则开始出现在0°方向上。

3.2 频率的影响

保持其他参数不变，控制单一变量荷载频率在5～25 Hz之间变化，分析荷载频率对地表振动响应以及与桩等距离各处响应差异的影响。地表振动和各方向响应差异随频率变化如图15～图17所示。

图15 地面振动响应随频率变化规律Fig.15 Variation of ground dynamic response with

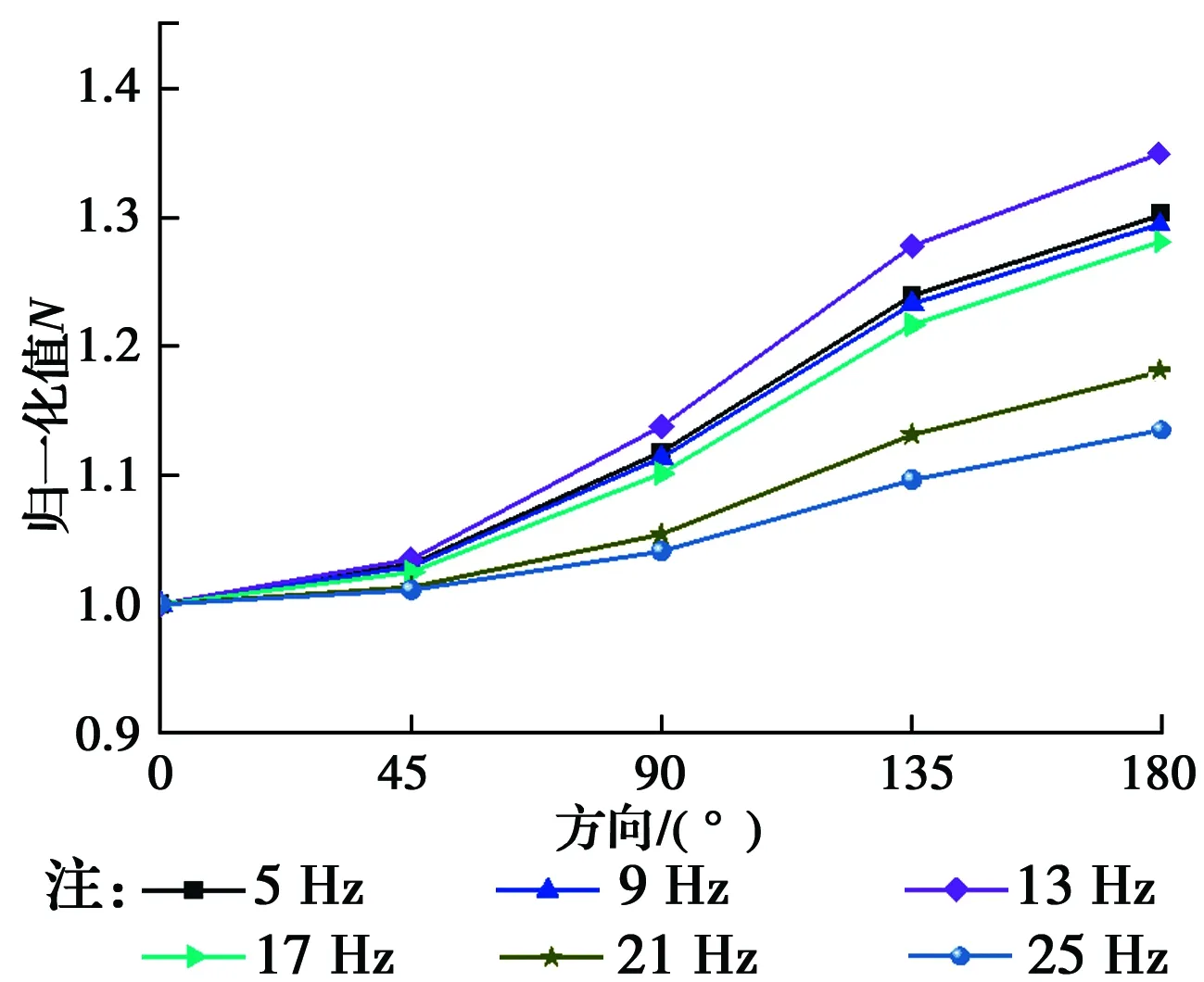
图16 r=38 cm环线上速度响应随频率变化Fig.16 Variation of velocity response with frequency for the case of r=38

图15表示地面距桩不同距离处速度峰值随荷载频率的变化规律。随着荷载频率增大，地面振动响应逐渐增大，且距桩越近速度峰值随频率增加越快，在距桩较远处，随荷载频率增加地面振动响应变化不大。当荷载频率在17 Hz以下时，振动速度峰值随频率呈线性增加；当频率大于17 Hz时，地表响应速度峰值增速逐渐变缓。

图16、图17给出了与桩等距离圆上各方向振动响应差异随频率的变化规律。当频率在13 Hz附近时，各方向的振动差异最为明显，之后，随着频率增加各方向的差异性逐渐减小，在距离较远处与桩同心圆上的各方向差异性显著大于较近处的响应差异。值得注意的是，随着频率的增加，在距离桩较远处与桩同心圆上振动响应最小值开始出现在45°方向上，即45°方向衰减速率开始变得最快。

3.3 桩长的影响

地面振动响应和与桩等距离各方向地表振动响应差异随桩长L变化规律分别如图18、图19所示。

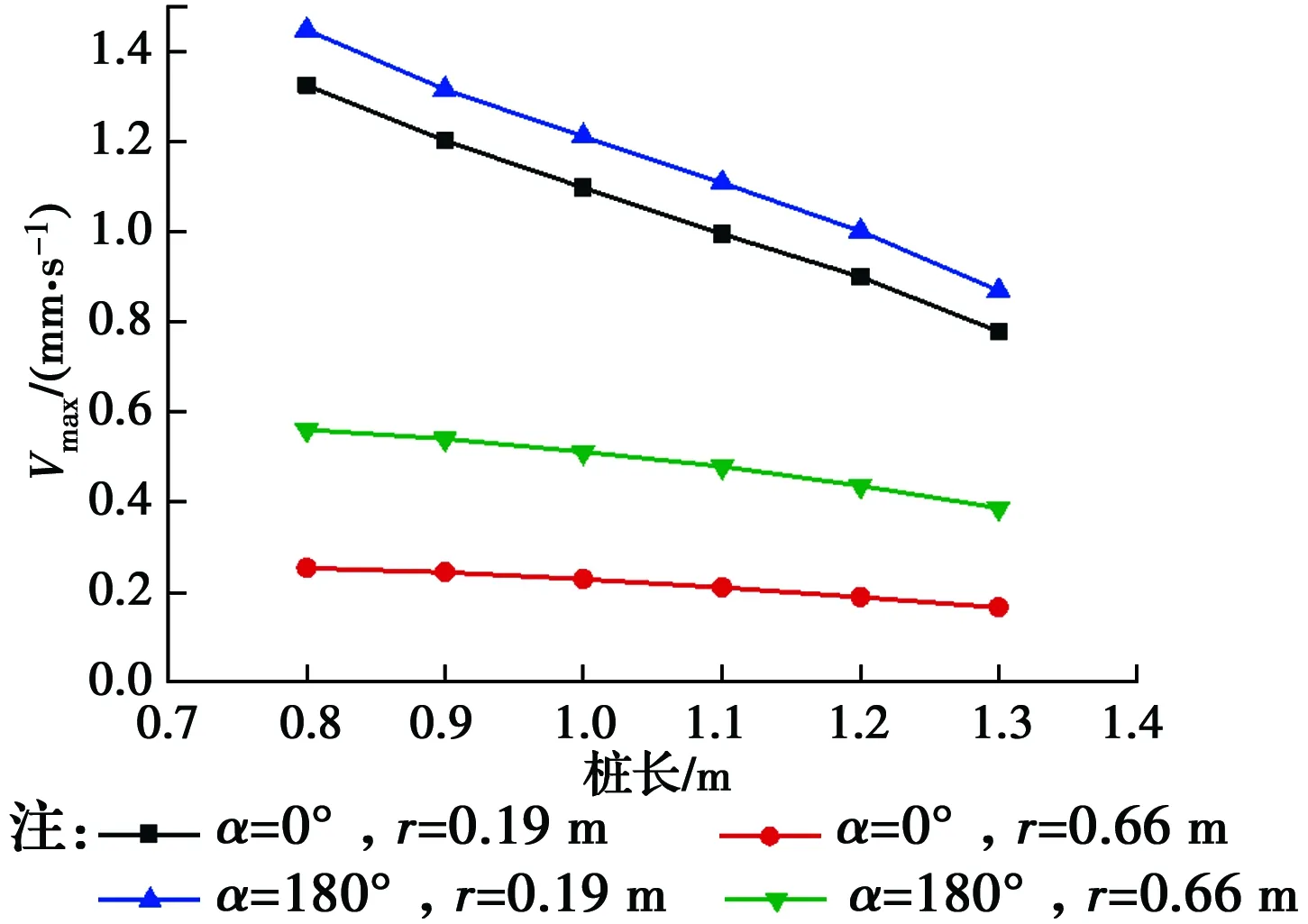
图18 地面振动响应随桩长变化规律Fig.18 Variation of ground vibration response with pile

从图18可以看出，地表振动响应随着桩长的增加呈线性减小，距桩较近处地表振动响应比远处减小更快，且在等距离的0°和180°方向减小速率较为一致，距离较远处0°和180°方向的速度峰值差异较大；图19给出了与桩等距离处(r=68 cm)各方向振动响应差异随桩长的变化规律。随着桩长的增加，各方向的速度响应差异逐渐增大，但影响并不明显；0°和45°的速度响应差异较小，从45°到180°方向速度响应差异开始急剧增大。

以上分析了基岩倾斜角度、荷载频率、桩长等参数对地表振动衰减的影响。由分析可知，基岩倾斜角度越大或桩长越长时，地面振动响应越小。在实际工程设计中，可以考虑通过增加桩长和合理选择地形位置来达到减小地面振动的效果。

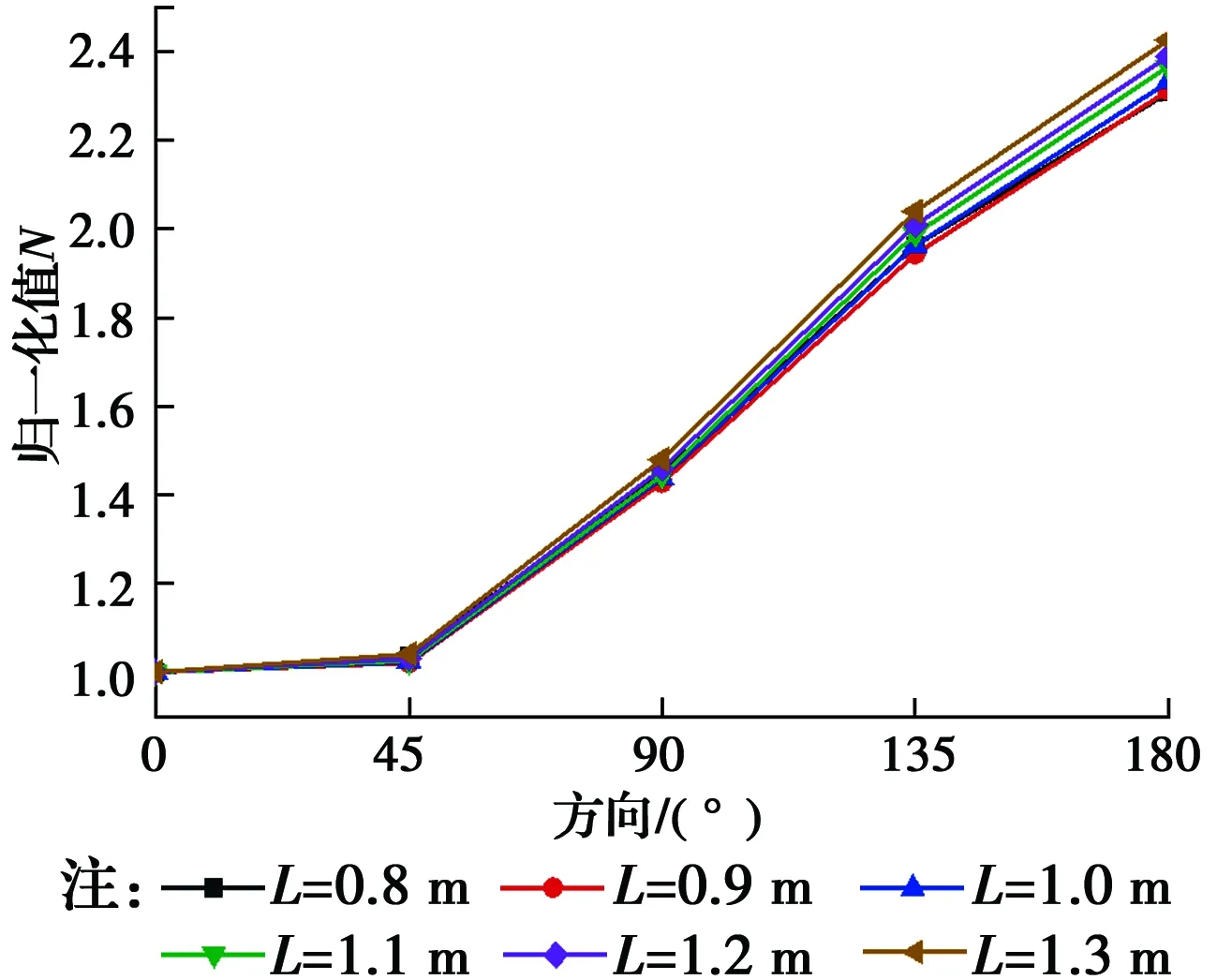
图19 r=68 cm环线上速度响应随桩长变化Fig.19 Variation of velocity response with pile length for the case of r=68

4 结论

通过模型槽试验与数值模拟相结合的方法，分析了倾斜基岩层地形条件下轨道交通引起地表振动的衰减规律，可以得到以下结论：

1)倾斜基岩条件下，地表振动响应呈现出方向差异化，一般沿基岩正下方衰减最慢，沿基岩正上方衰减最快，并从正下方到正上方衰减逐渐变快。

2)在地表与桩同心圆上，各方向速度响应存在差异性，且距离越远处差异性越大，从基岩正上方向到基岩下方向各点的速度响应峰值逐渐增大，但当基岩倾斜角度较小或荷载频率较大时，在距离桩较远处，同心圆上速度响应最小值会出现在与基岩正上方呈45°的方向上，这是受到频率、桩长、基底倾斜角度等因素的影响所致。

3)基岩倾角越大，地面振动响应越小，倾角变化对地表振动衰减规律也呈现方向差异化影响，在基岩正上方向，地面振动衰减随基岩倾角增大逐渐增快；在基岩正下方向，振动衰减规律不受角度变化影响。基岩倾角变化对与桩同心圆上各方向的振动响应差异化影响较为显著。

4)随着荷载频率的增加，地表响应速度先呈线性增大，然后增速变缓。频率对与桩等距离的圆上各方向速度响应差异性影响较为显著，当荷载频率为13 Hz时，各方向响应差异最大，然后随着频率增大，差异性逐渐减小。

5)地表速度响应随桩长增加呈线性减小，且距桩越近，速度响应减小越快，桩长变化对与桩等距离圆上各方向速度响应差异化影响并不明显。