基于中面模型和三维模型的气辅注射成型数值模拟及物理实验研究＊

任清海，王子剑，耿 铁

1.安阳职业技术学院机电工程系（河南安阳 455000）2.河南工业大学机电工程学院（河南郑州 450007）

1 引言

气体辅助注射成型（Gas-Assisted Injection Molding，简称GAIM）技术是在传统的注射成型和结构发泡成型基础上发展起来的一种被认为是注射成型技术史上的一次革命的新型注射成型技术[1～2]。在气体辅助注射成型过程中，由于塑料熔体流动本身就属于非牛顿流体在非等温条件下具有自由移动边界的流动问题，再加上气体注入型腔，发生气体和熔体两种性质完全不同物质的动力学相互作用，使得成型过程变得非常复杂，这使得人们有必要借助数值模拟技术来预测成型过程中各种缺陷、洞察缺陷的产生机理，实现虚拟试模和虚拟成型，从而指导、优化气辅模具设计和成型生产，提高模具上机成功率和生产效率。气体辅助注射成型数值模拟技术同传统的注射成型数值模拟技术一脉相承，都是在连续介质力学的理论基础上进行合理假设和简化来实现成型过程的数值模拟的，所以气体辅助注射成型数值模拟技术同样包括中面模型技术、双面流模型技术和三维模型技术，其中中面模型和双面流模型属于2.5维模型。

2 2.5维模型

最早的注射成型数值模拟技术是中面模型[3]，用户首先要将薄壁塑件抽象成近似的二维中间层，然后在这些中间层上生成二维平面三角网格，利用这些二维平面三角网格进行有限元计算，并将最终的分析结果在中间层上显示，如图1所示。实践表明，基于中面模型的注射成型数值模拟具有很大的局限性，其原因如下：其一，根据产品几何模型构造中面模型的操作起来非常困难，往往要花费大量的时间；其二，由于塑件的CAD模型和CAE分析模型不一致，这就需要把CAD模型导入CAE后进行再次建模。由此可见，基于中面模型的注射成型数值模拟技术在描述注射成型过程上真实性差，对实际的成型设计和控制的指导性较低，从而制约了注射成型数值模拟技术的发展。

图1 采用中面模型的模拟结果

双面流模型是一种产生于20世纪90年代后期的注射成型数值模拟技术，所谓双面流模型是指将塑件分成两部分，在塑件的表面划分有限元网格，在塑件的厚度方向上的有限差分。可见，双面流模型与中面模型本质上没有区别，双面流模型仅仅增加了一系列算法把中面模型的单一熔体流动扩展成沿着模型上下表面并实现一定协同的熔体流动[4～5]。由于几何模型结构的不规则性，将模型离散后，不能保证上下表面上的网格的形状、大小、节点位置等全部对称和一一对应，所以双面流模型也就存在一些先天性缺点：基于双面流模型的注射成型过程模拟中虽然计算了流动前沿厚度方向上的物理量，但并没有详细保存，从而造成分析数据不完整。另外，熔体的流动在厚度方向上未作任何操作，仅仅是沿着模型表面进行流动，这与实际情况不符，模拟结果缺乏真实感，如图2所示。

图2 采用双面流模型的模拟结果

中面模型和双面流模型的理论基础都是广义Hele-shaw薄壁流动假设，将三维流动问题分解为流动方向的二维和厚度方向的一维的所谓2.5维问题。广义Hele-shaw薄壁流动的控制方程如式1、2所示，其式中b为型腔半厚，u、v分别为x和y方向的平均流速。

熔体流动控制方程：

3 三维模型

在三维模型中，熔体在厚度方向的速度分量不再被忽略，熔体的压力、温度等参数沿厚度方向变化。因此，以三维模型为基础的流动模拟成为当今注射成型模拟领域中的研究方向和热点。在基于三维模型的分析计算中，采用三维控制体积追踪塑料熔体的流动前沿，并且考虑物理量在各个方向的影响，应用速度和压力同次插值的方法[6]，使得三维流动分析不仅能获得塑件表面的流动数据，还能获得塑件内部的流动数据，从而能准确地预测其充填行为，同时分析结果可以直接在三维塑件上或三维透明的模具型腔内显示，得到更加真实生动效果，如图3所示。

图3 采用三维模型的模拟结果

由于三维模型考虑了壁厚方向的影响，因此压力场、温度场等参数的求解都是三维的，在考虑粘性流体本构方程和合理假设的基础上对连续方程、动量守恒方程和能量守恒方程进行推导，得出用于熔体充填三维模拟的控制方程如式3所示[7]。

三维模型控制方程：

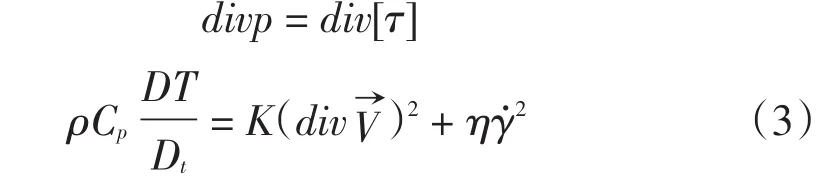
4 基于中面模型、三维模型的气体辅助注射成型数值模拟结果与实验结果的比较

基于前面对中面模型和三维模型的研究，作者采用MoldFlow模拟分析软件就同一气辅塑件分别进行了基于中面模型和三维模型的气体辅助注射成型数值模拟，并进行了物理实验研究，获得了基于中面模型和三维模型的气体辅助注射成型数值模拟结果以及实验结果。

为了便于比较两种不同模型的模拟计算结果，在模拟计算过程中，采用相同的气辅塑件结构、相同的成型工艺参数、相同的塑料材质和相同的网格尺寸。即工艺参数为：85%的熔体预注射量为，240℃的熔体温度，40℃的模具温度，1.5s的气体延迟时间，3MPa的气体压力，10s气体注射时间。塑料采用SK Corporation生产的牌号为Yuplene R370Y的PP塑料。中面模型采用边长为2mm的三角形单元离散气辅塑件的几何本体，并且采用一维管单元离散气辅塑件的气道部分，将其等效为圆形截面的气道，离散后的网格数量为6,420个；三维模型采用边长为2mm的四面体单元离散气辅塑件的整个几何体，离散后的网格数量为119,702个。

基于中面模型、三维模型的数值模拟和实验的气体穿透情况分别如图4、图5、图6所示。通过数值分析发现，三维模型的分析时间是5,245s，而中面模型仅需301s，可见采用三维模型模拟需要的时间较长，这是因为三维模型的四面体网格较中面模型的三角形网格的计算量多造成的，这也是目前采用三维模型所要解决的问题。

图4 中面模型的模拟结果

图5 熔体预注射量为85%的三维模型模拟结果

图6 熔体预注射量为85%的实验结果

将数值模拟结果与实验结果进行比较，熔体预注射量为85%时，采用中面模型的模拟结果显示熔体没有充满模具型腔，如图4a所示。将熔体预注射量提高到95%时，熔体才充满模具型腔，但是气指缺陷非常严重，如图4b所示。这都与图6所示的实验结果存在较大的差距。这是因为中面模型先天性缺陷造成的，也就是其在采用中面模型简化时忽略厚度方向的物理量计算造成的，从而造成模拟结果得到了较高的熔体预注射量，并且夸大了气指缺陷的程度，造成模拟结果与实际结果的偏差。

而图5所示的采用三维模型的气体穿透情况及气指缺陷情况都与图6所示的实验结果吻合的较好，也就是说采用三维模型的数值模拟结果能够比较真实、可靠的预测气体辅助注射成型效果。

5 结论

综上所述，通过物理实验，对模拟结果进行了验证，表明三维模型所用的时间较长，但模拟结果比中面模型的模拟结果更符合实验结果，可以提供比较真实、可靠的参考，不但可以提供定性的而且可以在一定程度上的提供定量指导作用。从分析结果和实验结果上来看，由于实际成型过程的影响因素很多，并不能一一在数值模拟计算中加以考虑，所以模拟分析结果与实验结果不能完全吻合，但是，基于三维模型的气辅成型数值模拟在很大程度上预测了塑件的成型过程，满足了优化模具设计、指导生产的需求。