自我追问:从被动接受到主动学习
——基于儿童视角的教材追问和学法转变
于正军
(扬州市江都区实验小学,江苏 扬州 225200)
儿童视角的课堂教学,需要创设“思起于疑,疑形于问”的学习情境,学生在课堂上的数学学习才会在疑问中思考、质疑中追问。如此教学,方能引领学生自主追问教材,释然心中疑惑。让“追问”成为数学概念建构的“助跑器”和思维症结的“溶解器”,促进学生的学习由被动接受走向主动思考,自然实现儿童视角的学法转变。
因此,教师对教材内容的把握和编排意图的理解,要基于儿童视角的追问,而不是一味地“尊重”教材的编排结构和内容,机械地服从和执行。教师在理解教材意图时,需要从儿童视角出发,从学生学习现实出发,对教材进行儿童视角的追问,这样才能有助教师把握教材知识的生长点,掌握学生的学习起点。笔者以苏教版四年级下册“用数对确定位置”教学为例,对教材展开儿童视角的自我追问,实现基于儿童现实的学习方法的自我转变和应然回归,促进学生从被动接受走向主动学习。
一、经验到重构:儿童数学表达的自我融合
追问一:为什么用“列和行”表示?
现实生活中物体的位置会因其所处的现实情境而用相应的描述方式给予确定。学生会根据自身的生活经验和认知水平选择合适的方位量词描述物体的位置,而不会机械地选用“列和行”的方式直接描述现实生活中物体的位置。因为用“列和行”描述位置关系适合在平面二维方向上确定位置,两个方向维度相互依存,缺一不可。
所以,教师在教学时如果强求学生用“列和行”的方式表示教室里学生的座位,既不符合学生的生活经验,也违背了学生的认知特点。学生会开展自我追问:为什么用“列和行”表示?此时,需要教师从儿童的认知经验和物体所处的现实情境出发,引导学生认知从生活现实走向生活情境,从现实生活中物体位置走向情境图中物体位置,继而引导学生的数学认知从生活表达走向情境表达,开展认知经验的必要重构,实现数学表达的自我融合。
如图1,教材主题图呈现的是教室座位的场景。在学生的认知经验里,描述座位时习惯用“第几组第几个、第几排第几个”等方式表达。在学生充分表达的基础上教师顺势引出:其实同学们所说的“第几组第几个、第几排第几个”都是在现实的教室里描述座位的位置,而回到例题情景图上,都可以直接用“在图上第几列第几行”的方式表示。这样学生对物体位置的确定就会自然从现实的座位场景中回归到情境图上来进行观察,如此学生就会产生用“列和行”表示情景图中小军位置的需求,实现了用“列和行”的方式描述小军位置的自我融合。这既遵循了学生的认知经验,又重构了学生的数学表达,迎合了学生的认知意愿,提升了学生的认知技能。

图1
二、习惯到认同:儿童数学经验的自我积累
追问二:为什么要“列在前、行在后”?
数学知识源于生活,又回归生活,凸显了数学与生活的紧密联系。故而,生活中的一切元素诸如人的认知方式、阅读习惯等都会影响着数学知识概念的自然建构。因此,教师在教学时要从学生的认知习惯和知识结构的特点出发,引领学生探索知识的形成过程,促进数学概念在学生的认知习惯中自然生成。否则,课堂上仍旧存在把知识的结论强加给学生,忽略知识形成的过程,抑制学生对知识主动求取的意识,学生丧失了对知识应用价值的深刻体会。
当学生在课堂上出现数“列数”和“行数”的顺序以及“列和行”的前后顺序不一致时,教师不能强迫要求学生:“在数列数时,一般从左往右,数行数时一般从前往后”,在用“列数”和“行数”表示位置时规定“列在前、行在后”。如此强加概念于学生进行教学,学生不但对知识的形成过程无法经历,而且会对本节课所学知识的价值无法体会,只会在教师的灌输下被动接受知识。
教学时理应从平面图形的特点和人的观察习惯出发,引领学生主动经历知识概念的形成过程。观察例题主题图时需要引导学生思考:从哪边开始观察?因为“从左往右”观察符合学生阅读时的习惯,因而学生在课堂上异口同声说“从左往右数”。教师顺势追问:在数“列数”时一般是从左往右数,在数“行数”时是从哪边开始数呢?由于学生平时在教室里已经形成“从前往后”观察座位的习惯,这一认知习惯促使学生一致认可从前往后(即图中从下往上)数“行数”。这样,数“列数”和“行数”方向的一致性就会在学生的观察习惯和认知经验里得到自然建构,并且在认知心理上形成了高度的情感认同。
学生统一了数“列数”和“行数”的观察方向后,教师围绕例题主题图继续引导:无论是“从左往右”还是“从前往后”数,在观察时都是从哪个点出发的?此时学生直观发现“列数和行数”的起点均始于座位图左下角的“0”起点,使平面图形中“横轴与竖轴”上的数在学生脑海里得到初步建立,加深理解平面图中“列数”与“行数”的对应关系。
三、情境到模型:儿童数学思想的自我感悟
追问三:为什么例题主题图从座位情境图变成圆点图?
学数学本质是培养思维。数学思维的培养方式离不开引导学生推理、抽象、模型。教师在引领学生探究新知的过程中,既要让学生经历知识概念的形成过程,更要让学生探寻数学现象的规律和模型,在感受数学应用的普遍性和必要性过程中,感悟数学基本思想,掌握数学思想方法。
因此,教学时,教师不能机械地直接出示例题圆点图(参见图2):“现在用圆点表示学生的座位,你能找到小军的位置吗?”如此唐突地直接出示圆点图,学生既无法感受到数学符号的模型意义,也无法体会到用“列与行”的方式确定物体位置的广泛性和抽象性,同时心中还会生疑:为什么要变成圆点图表示座位图呢?
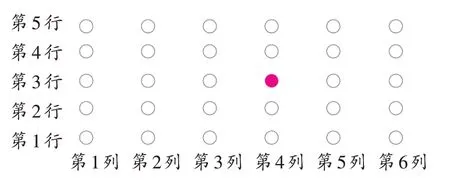
图2
由此,教师需要从数学知识的应用价值和学生的认知经验出发,引导学生围绕例题主题图讨论交流:像这样用“列和行”来确定位置时有什么好处呢?促使学生发现:从列和行两个方向能准确地确定学生的座位位置。继而引导拓展:这样确定位置的方法还可以用在什么地方?学生交流后得出:体育课队形、合唱社团队形、围棋棋子的位置。还有学生插话:“只要有‘列和行’的地方都可以……”在学生回答的基础上,教师顺势引出圆点图:“是的,现在老师就用这样一个圆点图来表示大家所说的生活中有‘列和行’的地方。”学生在交流过程中,自然体会圆点平面图的模型意义,以及用“列和行”的方式来描述平面图中点的位置的广泛性和抽象性。如此从情境到具体、从具体到抽象、从抽象到模型的知识建构过程,符合了儿童的认知情感和数学概念的知识结构,为进一步激发学生用数学的方式表示平面图中点的位置提供了思维支撑。
四、形式到内容:儿童数学方法的自我建构
追问四:为什么要用(4,3)这样的形式表示?
数学概念的“内容”与“形式”是一对相互依存的统一体。“内容”发生变化时,对“内容”进行数学表达的“形式”,也会发生相应的变化。当学生经历了从现实的生活场景到例题情境图,再到抽象的圆点平面示意图,学生确定物体位置的表达方式经历了“多元化→规范化、具象化→抽象化、文字化→数字化”三次“数学化”过程。因此教学时,教师要善于引导学生根据确定位置的具体“内容”探索合适的“形式”,体会与感悟“内容”决定“形式”、“形式”服务于“内容”的数学哲学思想。
课堂上观察发现,学生确立了用“列和行”表示位置方法后,自然地用纯数字的方法替代了用文字表示的“第几列第几行”。这一认知需求符合学生的认知特点和年龄特征,喜欢追寻简单而方便的表示方法。此时亟需教师启迪学生回顾反思:用什么样的方式来表示物体的位置,需要根据物体的具体“内容”确定。在描述例题主题图中小军的位置时,可以说成“在图中第几列第几行”,而在这样一个圆点示意图上,怎样才能简洁而又准确地表示出这个平面示意图中点的位置呢?
引导学生进一步思考:(1)要确定平面图中点的位置,观察一个方向行吗?为什么?(2)列和行的位置可以怎么表示?你怎么想到的?(引导学生观察图中横轴与竖轴上的数)(3)用这两个方向上的数来确定图上点的位置,你觉得可以怎样把这两个数组合在一起?(4)你能给这个“组合”起个名称吗?在学生经历了如此的认识与交流后,教师顺势引出“数对”的规范表达方式,并引导学生直观体会其意义:平面图上点的位置的确定既要知道“列数”也要知道“行数”,两者缺一不可,需要用一个小括号让“列数”和“行数”合为一个整体,并在中间用逗号隔开。如此引导学生自主建构“数对”的概念含义,学生对用“(4,3)”形式表示小军位置的符号意义的“内容”与“形式”理解深刻,应用自然。
五、知识到能力:儿童数学认知的自我加工
追问五:为什么横轴上的数表示“列数”,竖轴上的数表示“行数”?
学生在掌握数学知识的同时,如果相应的思维能力未能得到同时发展,说明课堂教学的“知识”与“能力”目标未能同时有效达成。因此,教师在预设教学内容的背后,要思考学生在掌握知识的过程中,支撑知识理解的思维能力能否形成。如果教师只是单一完成“知识目标”,而不关注“能力目标”,学生对所学知识的理解只是表层的、短暂的,缺乏深入与持久。只有关注知识概念背后的思维元素,教学才能促进学生主动学习,学生的思维缺口才能得到及时弥补,知识与能力方能同步发展。
在教师引出用“数对”表示平面图中点的位置后,学生脑海里的“列”的概念特征是竖轴、观察的方向是上下观察,“行”的概念特征是横轴、观察的方向是水平观察。而平面图中横轴上的“数”却表示“列数”,竖轴上的“数”却表示“行数”。即先看横轴上的“数”,再看竖轴上的“数”,这与“数对”强调的“列在前、行在后”确定位置的方法在“数学视觉”上产生了冲突,此时留在学生头脑中的“列与行”的认知思维开始模糊与茫然。
所以,教师不必在课堂上要求学生强行记忆“列在前、行在后”的数学概念,只需要引导学生在确定平面图中点的位置时掌握观察的方向和应有的习惯,让学生对认知思维进行自我加工和调控。从学生认知思维的现实特点出发,引导学生思考:在确定格点图中点的位置时,依然先左右方向观察,横轴上看到的“数”就是“列数”,然后再上下方向观察,竖轴上的“数”就是行数。这样学生对于“列与行”思维认知就会得到自我加工与调控,形成统一的数学认知:用“数对”确定平面图上点的位置,与平时的自我认知习惯是一致的,先左右观察后上下观察,继而感受到与“数对”中“列在前、行在后”的确定位置方法的一致性。如此设计,就会实现从教师机械强调“列在前、行在后”的直接“灌输”到学生认知思维的自我加工的应然转变,有效促进学生对知识概念的意义建构和思维能力的同步发展。
综上所述,数学概念的教学,只有坚持儿童视角的教材追问,才能使“学习现实”“教学现实”“教材现实”在教学中得以自然融合,凸显“儿童主人”地位的课堂才能真正实现,传统的被动接受的课堂模式才会被自主学习型的新时代课堂所替代,学生的核心素养和必备能力才能在数学课堂上得到永恒的培养与提升。▲

