跨越断层建构模型

孔荷红 孔忠伟

2014年9月开始，人民教育出版社新增修订小学数学三至六年级教材，其中对解决问题版块有较大幅度的改进，每一册教材都新增了相应的解决问题内容。不管从教材习题的编排，习题本身以及习题教学要求，都与老版教材有较大的改动。纵观整册小学数学新修订版教材，四年级解决问题不管从习题内容，还是习题数量，都明显少于其他年级。但四年级又非常重要，它不仅是学生整数运算学习的重要阶段，同时也为五年级的方程解决问题打下基础。而现在的教材编排，从某种角度来说，四年级的解决问题教材有一定的断层，而且也缺少典型类型的学习与提炼。本文主要研究四年级两积之和的解决问题，通过化零为整，帮助学生跨越断层;注重数形结合，促进学生建构模型，从而帮助学生提升解决问题的能力，为今后数学学习打下基础。

一、四年级解决问题教材分析

（一）内容断层

从整体上来看，三年级有关解决问题教学的内容很多，同时它的定位也比较清晰，有归一问题、归总问题，连乘或连除等。这些模型的教学，可以帮助学生更好地理解与迁移，也有利于教师教学。但四年级的解决问题教学，只有两个常用的模型，运用单价、数量和总价以及速度、时间和路程，而且计算也都只需一步。五年级的解决问题教学，以方程的解决问题教学为主，而方程的主要结构，也以两积之和ax+bx=c的结构为主。

断层一：解决问题难度，提升不明显

三年级的解决问题以两步计算为主，比如三年级上册的归一、归总问题，三年级下册的连乘与连除问题等。但到了四年级的解决问题例题，只有简单一步关系的运用，比如单价、数量和总价或者速度、路程和时间等，缺少复杂问题的练习。而到了五年级，学生对于方程问题又需要三步计算，因此四年级对于解决问题的编排，不管是习题类型，还是解决难度，都有一定的断层，没有给学生合适的基础来适应五年级解决问题。

断层二：解决问题模型，没有相应支持

五年级的几个方程常用模型，都需要建立在两积之和的基础之上，但四年级解决问题的教材中，并没有两积之和的专题解决问题的教学。反而在各单元零散会出现一些习题。这样的习题教学，肯定不利于学生去提煉和学习，学生如果对这种结构不熟练，肯定会影响其后续两积之和方程的学习。

（二）分布零散

仔细分析四年级数学解决问题的一些习题，发现两册教材中也有一些零散的两积之和结构的例题或习题。但由于习题分散，而且不同的单元都有自己的教学任务，不利于学生去提炼和感悟两积之和的结构。

比如，人教版四年级教材第四单元《三位数乘两位数》P50。

学校要为图书馆增添两种新书，每种买3套。一共要花多少钱？

在该习题中，虽然有着两积之和的模型，但由于教材是需要各买3套，教师比较容易会把解决问题的重点放在运算定律的讨论，而弱化了其中两积之和的结构。而且仅有一道习题的练习，肯定不利于学生整体感悟结构。

二、有效的策略

面对以上这些现象，笔者认为教师一定要善于整合教材，基于数形结合，多角度、多形式来帮助学生跨越断层，建构模型，从而帮助学生不断提升解决问题的能力，为五六年级的数学解决问题学习打下扎实基础。

（一）化零为整，跨越断层

化零为整，跨越断层，主要是教师要整体呈现结构相同的习题，通过比一比，解一解，编一编等多种形式来帮助学生掌握解决问题的方法，提升解决问题的能力。

1.化散为整，整体呈现

在四年级人教版教材或其他练习中，有着大量结构相同的习题，其中也有两积之和的习题。化散为整需要教师精心选择习题，并把结构相似的习题进行整体呈现，引导学生在解答、比较与归纳中感悟两积之和的模型。

例如，上面的四道习题（如图一），来源于配套习题，并适当进行了修改。这些习题都需要利用两积之和的结构来解决问题。通过让学生集中练习，有利于学生提炼与感悟模型。

2.化解为变，整体改编

学生解决问题能力的提升需要建立在大量的习题练习之上，但数学学习的时间非常有限，因此有效提升解决问题的能力，就需要把一类题型或一种题型练得更透。“化解为变”就是以其中一道题目为素材，通过条件或问题的不断变化，在变与不变中展开练习，从而提升解决问题的能力。

例如，在上题中，当我们解决了一题习题后，要求学生把其中一个信息改成问题，编出一道题目。学生通过编一编，算一算，由于计算不成问题，学生可以较快解决所有问题。因而就给了学生更多练习的机会，提升了解决问题的能力。

3.化变为联，整体迁移

建构主义理论认为：知识的学习需要建立在学习者已有经验的基础之上，因此，教师需要不断帮助学生把新知与旧知结合起来，形成新的知识链。而化变为联就是帮助学生在不断变化中联系旧知，从而帮助学生更好地融合知识，提升解决问题的能力。

通过变式，教师引出了上题（如图），其中最大的变化就是去掉了两种水果的数量，改成了两种水果的数量之和。这样的变式主要是为了帮助学生感受到两积之和的问题与鸡兔同笼问题之间的联系，从而帮助学生深入感悟模型，提升解决问题的能力。

（二）数形结合，构建模型

数学模型的建立需要经历多个阶段，笔者认为一般需要经历初步感悟、提炼模型、深入感悟、运用模型等环节。在这些环节中，数形结合使学生从模糊到清晰，从陌生到熟练，从学习到迁移。借助数形结合，可以更好地帮助学生构建模型，提升解决问题的效率。

1.情境创设融入数与形，初步感悟

在情境创设引入新课时，设计数形结合的习题，不仅可以调动学生的学习兴趣，同时也为学生初步建立数与形之间的联系埋下伏笔。学生借助图的直观，可以初步感悟两积之和模型。

例如，图一的四道习题，教师就呈现了不同类型的习题，其中就有纯文字和纯图形的习题。这样数形结合的情境，可以让学生更好地开展对比与交流，可以帮助学生更好地初步感悟模型。

2.思维关键求联数与形，提炼模型

数学模型的提炼需要学生不断通过比较，在不同的情境中寻找相同的关系。借助图形的直观，教师需要引导学生去沟通形与数之间的关系，从而使学生发现数中的关系与形的数量是一样的，都是利用相同的结构，从而逐渐提炼两积之和的模型。

例如，在上题的情境中（如上图），当让学生来寻找习题的相同点时，大多数学生都会先找到数与形之间的联系，既大长方形的面积等于苹果的总价，小长方形的面积等于梨的总价。教师还可以追问：“明明是面积，为什么会等于总价呢？”通过引导学生思考与比较，学生就会发现大长方形的长和宽与苹果的单价和数量之间的联系，从而帮助学生深入理解两积之和结构。

3.思路变化凸显数与形，深入感悟

为了让学生更好地理解模型，运用模型，教师还需要不断变式习题，从变与不变中去帮助学生深入感悟模型。而借助数与形的变式，则可以更直观呈现不同变式下的相同点，帮助学生深刻理解模型。

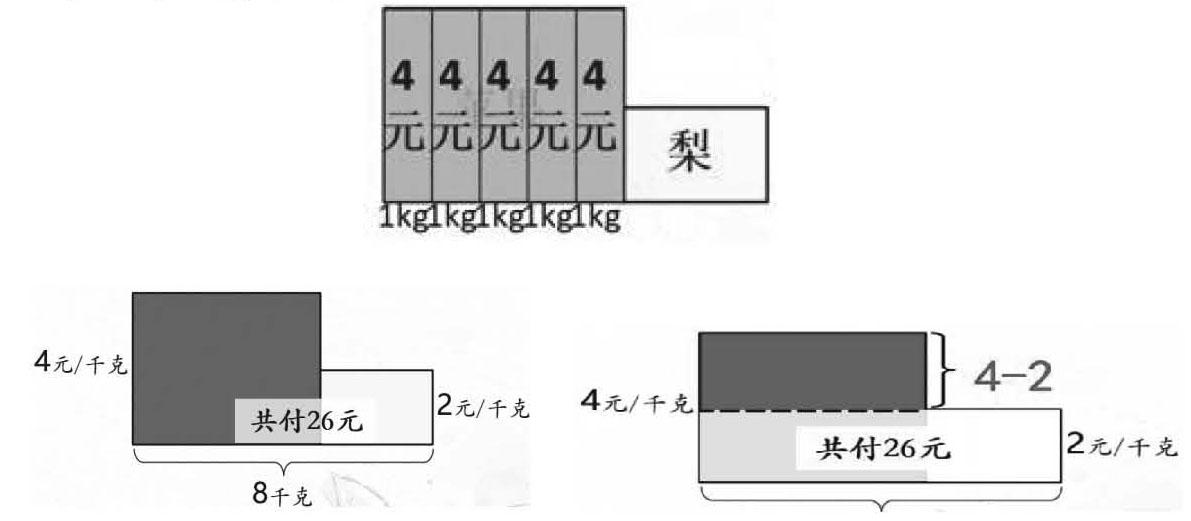
例如，在两积之和的最后环节（如上图），我们设计了变式练习，把习题改成了“李红买苹果和梨共付26元，蘋果每千克4元，梨每千克2元，两种水果共买了8千克。买了几千克苹果和几千克梨？”为了帮助学生理解，可以把8千克全部看成2元，上面黑色的长方形就是10元，利用10元去除以两种水果的单价，就可以算出大长方形的长是5千克，那么剩下的小长方形的宽就是3千克。这样直观呈现假设的图形，可以帮助学生理解其中的方法，突破难点。

关注习题的研究，教师需要更深入了解习题练习的目的，不断通过整合、对比、建模等帮助学生深入学习解决问题，感悟其中的本质，提升解决问题的能力。相信，通过不断研究一定能较好地促进学生解决问题能力的发展。

作者单位  浙江省杭州市萧山区渔浦小学  浙江省杭州市滨文小学