比色法测定猪饲料中亚硝酸盐含量的不确定度评定

魏桂云，林艳秋，李郁，黄铭辉，刘芳，刘华丰

（福建省产品质量检验研究院，福建 福州 350002）

测量不确定度是一个合理表征测量结果分散性的参数，报告测量不确定度就是对测量结果质量的定量表征。测量不确定度的大小往往影响着科研试验的水平，因此需要对测量结果的不确定度进行评定。JJF 1059.1-2012《测量不确定度评定与表示》中规定，完整的测量结果应报告被测量的估计值及其测量不确定度以及有关的信息[1]。试验依据GB/T 13085-2018 《饲料中亚硝酸盐的测定 比色法》[2]的测定原理和方法，建立相应的数学模型，运用测量不确定度评定的基本方法，对模型中各影响因素的不确定度进行计算和评定[3]。

1 材料与方法

1.1 试剂

硫酸锌(120 g/L)、氢氧化钠溶液(20 g/L)、乙酸溶液（60%）、氯化铵缓冲溶液（量取500 mL水于1 L容量瓶，加入20mL盐酸，混匀，加入50mL氨水，用水定容至刻度，调节pH至9.6～9.7）、对氨基苯磺酸溶液(5g/L)、盐酸萘乙二胺溶液(1gL)、显色剂(临用前将对氨基苯磺酸溶液和盐酸萘乙二胺溶液等体积混合)。

1.2 仪器

紫外可见分光光度计（UV-2700）：日本岛津公司(KYOTO)；

电子天平（感量0.0001g）：德国赛多利斯科学仪器（北京）有限公司。

1.3 标准溶液的配制

精确称取250.0 mg经(115±5)℃烘至恒重的亚硝酸钠，加水溶解，转移至500 mL容量瓶中，加100 mL氯化铵缓冲液，加水稀释至刻度，混匀，临用前，移取1.00 mL上述溶液于100 mL容量瓶中，用水稀释至刻度，混匀。

1.4 样品处理

称取约5 g试样(精确到0.001 g)，置于200 mL锥形瓶中，加70 mL水和1.2 mL氢氧化钠溶液，混匀，用氢氧化钠溶液调节pH至8～9，加入10 mL硫酸锌溶液，混匀，置于60 ℃水浴中加热10 min，取出后冷却至室温，全部转移至200 mL容量瓶中，加水至刻度，混匀。放置30 min，过滤，弃去初滤液约20 mL，收集剩余滤液为试液。分别移取2份10.0 mL试液于25 mL容量瓶a和b中，在容量瓶a中加入4.5 mL氯化铵缓冲溶液、2.5 mL乙酸溶液后用水定容至刻度，混匀；在容量瓶b中加入4.5 mL氯化铵缓冲溶液，2.5 mL乙酸溶液后立即加入5.0 mL显色剂，用水定容至刻度，混匀，避光放置25 min后在波长538 nm处，以容量瓶a溶液为试样参比，测定容量瓶b溶液的吸光度值。

1.5 亚硝酸盐标准曲线的制备

分别准确移取0、0.4、0.8、1.2、1.6、2.0 mL亚硝酸钠标准工作液于25 mL容量瓶，各加入4.5 mL氯化铵缓冲液，2.5 mL乙酸溶液后，立即加入5.0 mL显色剂，定容摇匀，避光静置25 min，测定吸光度。

2 数学模型的建立与不确定度来源分析

2.1 建立数学模型

根据亚硝酸盐（以亚硝酸钠计）含量的计算公式建立数学模型，如下：

式中：

X为样品中亚硝酸盐的含量，mg/kg；

m1为试样质量，g；

m2为测定用试液中亚硝酸盐的含量，μg；

V1为样品处理后试液的总体积，mL；

V2为测定用试液的体积，mL；

1000为单位换算系数。

2.2 识别和分析不确定来源

通过测量过程及数学模型分析，猪饲料中亚硝酸盐含量测定的不确定度来源主要包括样品质量的不确定度、测定用试液中亚硝酸盐含量的不确定度、样品定容体积不确定度、测定用试液体积的不确定度及重复性引起的不确定度。

3 不确定度分量的评定

3.1 样品称量的不确定度urel(m1)

样品称量质量为5 g，天平鉴定证书给出的质量允许误差为±0.15 mg，为B类评定，假设在区间内为均匀分布，则：

相对标准不确定度

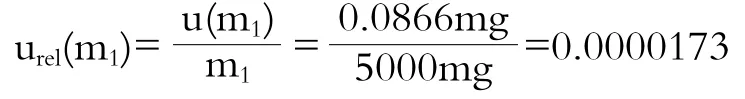
3.2 测定用试液中亚硝酸盐的含量的不确定度urel(m2)

3.2.1 亚硝酸钠纯度引起的不确定度urel1(m2)

分析纯亚硝酸钠含量(≥99.0%)引起的不确定度，允许误差为1%，按照矩阵分布处理，包含因子

相对标准不确定度

3.2.2 标准使用液配制带来的不确定度urel2(m2)

标准使用液配制带来的不确定度包括标准物质称量带来的不确定度、定容所用容量瓶不确定度及稀释过程移液管带来的不确定度。

3.2.2.1 标准物质称量不确定度urel2.1(m2)

标准物质称取量为250.0 mg，天平鉴定证书给出的质量允许误差为±0.15 mg，为B类评定，假设在区间内为均匀分布，则:

相对标准不确定度

3.2.2.2 定容用500 mL容量瓶体积带来的不确定度urel2.2(m2)

⑴根据JJG 196-2006《常用玻璃量器检定规程》[4]的规定，A级500 mL容量瓶的容量允差为±0.25 mL，假设按照三角形分布处理，则：

容量瓶体积带来的不确定度

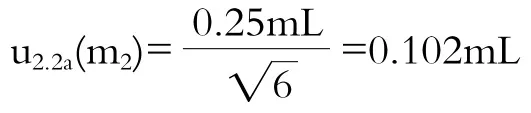
⑵温度引起体积变动的不确定度u2.2b(m2)：使用容量瓶校准是在20℃条件下，而实验室的温度在±4 ℃之间变动，该影响引起的不确定度可通过估算该温度范围和体积膨胀系数来进行计算。液体的体积膨胀明显大于容量瓶的体积膨胀，因此只需要考虑前者即可。水的体积膨胀系数为2.1×10-4/℃，产生的体积变化量为：

体积×膨胀系数×ΔＴ=500×2.1×10-4×4=0.420 mL

假设温度变化是矩形分布，则

⑶定容至刻度的变异性引起的不确定度u2.2c(m2)：通过对典型的500 mL容量瓶充满10次并称量（表1），得出标准偏差为0.0328 mL，由此引入的不确定度分量u2.2c(m2)=0.0328 mL。

所以500 mL容量瓶带来的不确定度：

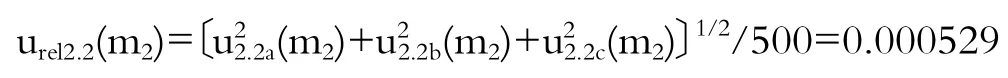
表1 500 mL容量瓶定容重复性数据

3.2.2.3 定容用100 mL容量瓶体积带来的不确定度urel2.3(m2)

⑴根据JJG 196-2006《常用玻璃量器检定规程》[4]的规定，A级100 mL容量瓶的容量允差为±0.10 mL，假设按照三角形分布处理则：

容量瓶体积带来的不确定度

⑵温度引起体积变动的不确定度u2.3b(m2)

使用容量瓶校准是在20 ℃条件下，而实验室的温度在±4 ℃之间变动，该影响引起的不确定度可通过估算该温度范围和体积膨胀系数来进行计算。液体的体积膨胀明显大于容量瓶的体积膨胀，因此只需要考虑前者即可。水的体积膨胀系数为2.1×10-4/℃，产生的体积变化量为：

体积×膨胀系数×ΔＴ=100×2.1×10-4×4=0.0840 mL

假设温度变化是矩形分布，则

⑶定容至刻度的变异性引起的不确定度u2.3c(m2)

通过对典型的100 mL容量瓶充满10次并称量（表2），得出标准偏差为0.0443 mL，由此引入的不确定度分量u2.2c(m2)=0.0443mL。

所以100mL容量瓶带来的不确定度:

表2 100 mL容量瓶定容重复性数据

3.2.2.4 稀释过程移液管带来的不确定度urel2.4(m2)

⑴根据JJG 196-2006 《常用玻璃量器检定规程》[4]的规定，A级1 mL移液管的容量允差为±0.007 mL，假设按照三角形分布处理则：

⑵温度引起体积变动的不确定度u2.4b(m2)

移液管校准是在20 ℃条件下，而实验室的温度在±4 ℃之间变动，该影响引起的不确定度可通过估算该温度范围和体积膨胀系数来进行计算。液体的体积膨胀明显大于容器的体积膨胀，因此只需要考虑前者即可。水的体积膨胀系数为2.1×10-4/℃，产生的体积变化量为:

体积×膨胀系数×ΔＴ=1×2.1×10-4×4=0.000840 mL

假设温度变化是矩形分布，则

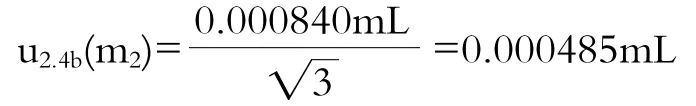
则1mL移液管带来的不确定度:

标准溶液配制带来的不确定度

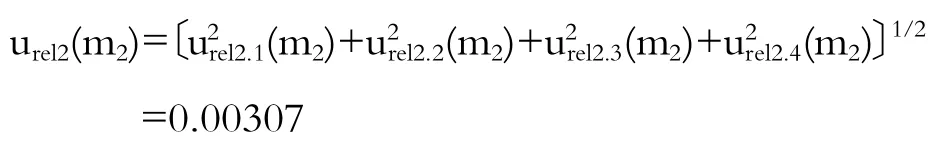
3.2.3 绘制标准曲线带来的不确定度urel3(m2)

3.2.3.1 移液管使用带来的不确定度urel3.1(m2)

⑴根据JJG 196-2006《常用玻璃量器检定规程》[4]的规定，A级2 mL移液管的容量允差为±0.010 mL，假设按照三角形分布处理则：

⑵温度引起体积变动的不确定度u3.1b(m2)

实验室的温度变化±4 ℃，水的体积膨胀系数为2.1×10-4/℃，产生的体积变化量为

体积×膨胀系数×ΔＴ=2×2.1×10-4×4＝0.00168mL

假设温度变化是矩形分布，则

则2 mL移液管带来的不确定度

3.2.3.2 标准曲线拟合引入的不确定度urel3.2(m2)，B类不确定度

⑴按试验方法测得标准系列的吸光度（表3）。

表3 标准系列及对应吸光度

由表3得曲线回归方程：

y=0.0178x-0.0003，曲线斜率b=0.0178，曲线截距a=-0.0003

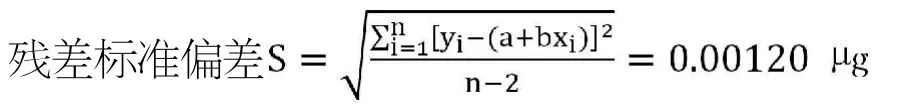
对测定用样液进行2次测量，即p=2，测得样液中亚硝酸盐含量c0=1.76 μg。

标准不确定度

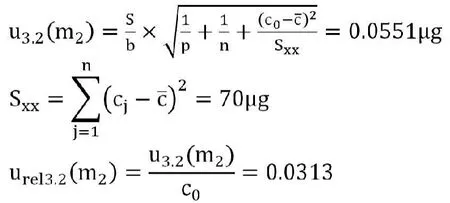
由此绘制标准曲线带来的不确定度urel3(m2)

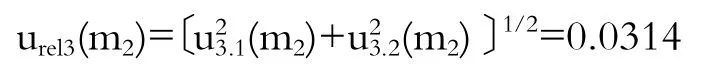
根据上述各影响因素的不确定度求得试液中亚硝酸盐的含量的不确定度urel(m2)

3.3 样品定容体积不确定度urel(V1)

3.3.1 根据JJG 196-2006《常用玻璃量器检定规程》[4]的规定，B级200 mL容量瓶的容量允差为±0.30 mL，假设按照三角形分布处理则：

容量瓶体积带来的不确定度

3.3.2 温度引起体积变动的不确定度u2(V1)

使用容量瓶校准是在20 ℃条件下，而实验室的温度在±4 ℃之间变动，该影响引起的不确定度可通过估算该温度范围和体积膨胀系数来进行计算。液体的体积膨胀明显大于容量瓶的体积膨胀，因此只需要考虑前者即可。水的体积膨胀系数为2.1×10-4/℃，产生的体积变化量为：

体积×膨胀系数×ΔＴ=200×2.1×10-4×4＝0.168 mL

假设温度变化是矩形分布，则

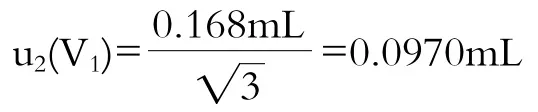
3.3.3 定容至刻度的变异性引起的不确定度u3(V1)

通过对典型的200 mL容量瓶充满10次并称量，（见表3）得出标准偏差为0.0387 mL，由此引入的不确定度分量u3(V1)=0.0387 mL。

所以200mL容量瓶带来的不确定度:

表3 200 mL容量瓶定容重复性数据

3.4 测定用试液体积的不确定度urel(V2)

3.4.1 根据JJG 196-2006《常用玻璃量器检定规程》[4]的规定，A级10 mL移液管的容量允差为±0.020 mL，假设按照三角形分布处理则

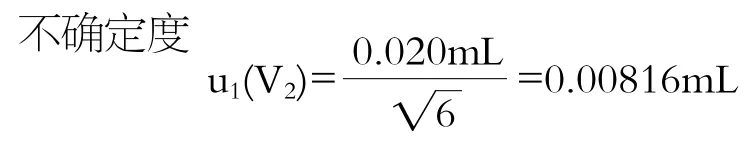
3.4.2 温度引起体积变动的不确定度u2(V2)

移液管校准是在20 ℃条件下，而实验室的温度在±4 ℃之间变动，该影响引起的不确定度可通过估算该温度范围和体积膨胀系数来进行计算。液体的体积膨胀明显大于容器的体积膨胀，因此只需要考虑前者即可。水的体积膨胀系数为2.1×10-4/℃，产生的体积变化量为：

体积×膨胀系数×ΔＴ=10×2.1×10-4×4＝0.00840 mL

假设温度变化是矩形分布，则

测定用试液体积的不确定度urel(V2)

3.5 检测方法重复性引入的不确定度urel(X)

在重复性条件下，独立测试猪饲料样品T=6次，结果分别为6.43、6.50、 6.60 、6.79 、6.88、6.68 mg/kg，其算术平均值为X=6.65 mg/kg。

以极差法求其不确定度，极差R=0.45 mg/kg,极差系数C=2.53，则

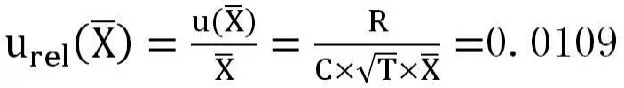
3.6 合成标准不确定度u(X)

根据各分量的相对不确定度，合成标准不确定度

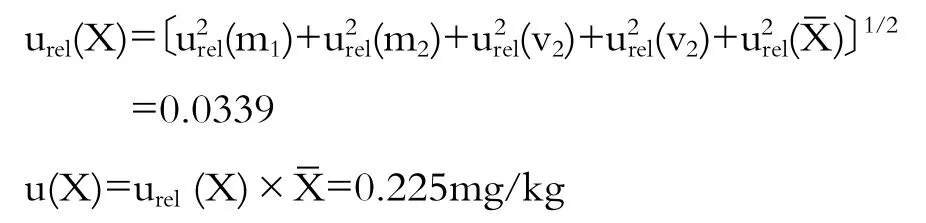
4 结果的报告

取置信概率95%，包含因子k=2，评定扩展不确定度

猪饲料中亚硝酸盐（以亚硝酸钠计）含量检测结果：（6.65±0.45）mg/kg

5 讨论

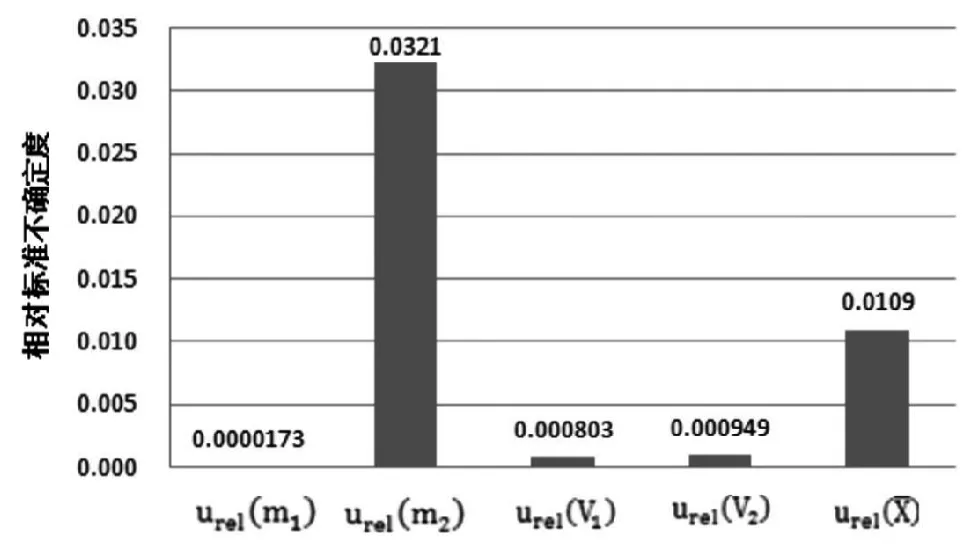
图1 urel(X)合成不确定度分量

图2 urel(m2)试液中亚硝酸盐含量的不确定度分量

猪饲料中亚硝酸盐含量为6.65 mg/kg时，扩展不确定度U(X)=0.45 mg/kg，包含因子k=2。通过对各不确定度分量的识别、分析和量化，可以知道测定用试液中亚硝酸盐含量的不确定度占比最大（图1），在urel(m2)中又以绘制标准曲线带来的不确定度为最(图2)，因此在试验过程中要严格控制好标准曲线绘制，从而得到更精准的试验结果。