两个竞赛试题的推广

魏国祥

（四川职业技术学院 应用数学与经济系，四川 遂宁 629000）

试题1（第二届陈省身杯全国高中数学奥林匹克试题）对任意不全为零的实数x,y,z，求证：

试题2（2016 年福建省高中数学竞赛试题）当x,y,z 为正数时的最大值为______.

文[1]运用球面形式的三角代换求解了上面两个题目，但过程较为繁杂.

其实，试题1 的一般情形为：设p,q 是两个正常数,对任意不全为零的实数x,y,z，求的最大值.

由均值不等式可知，对任意正数k，恒有

仅当y = z 且kx2=( y + z)2时等号成立.即知

试题2 的一般情形为：设p,q 是两个正常数,对任意不全为零的实数x,y,z，求的最大值.

由均值不等式可知

我们将上面两种情形的问题一般化成下面问题.

问题设p,q,r 是不全为零的三个非负数，对任意不全为零的实数x,y,z，求的最大值.

我们发现这个问题很难运用文[1]的球面形式的三角代换方法来求解，也很难用均值不等式来解决.但从这个问题的结构这让我们想起了被称为母不等式的嵌入不等式.

嵌入不等式对三角形ABC 与实数x,y,z，恒有

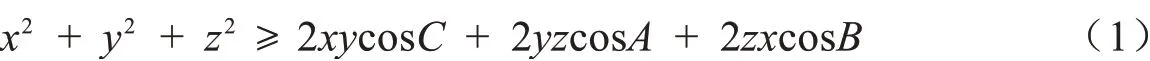
（1）式等价于显然成立的不等式( ycosC + zcosB - x)2+ ( ysinC - zsinB)2≥0，

当且仅当x:y:z = sinA:sinB:sinC 时（1）式等号成立.

由（1）式可知

由于sinA = sin( B + C ) = sinBcosC + cosBsinC，

即sinA - sinBcosC - sinCcosB = 0，依此理我们可得

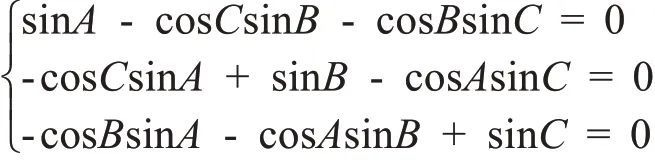
这是一个关于sinA,sinB,sinC 的三元一次齐次方程组，它有非零解的充要条件为

即

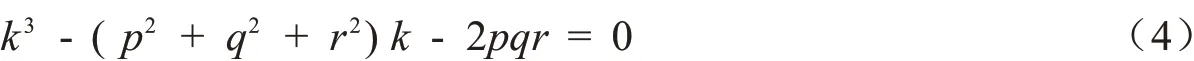
这是一个关于k 的一元三次方程，它存在唯一的正根，理由为：设三个根为k1,k2,k3，若pqr = 0，则；若pqr ≠0，由根与系数的关系可知，k1+ k2+ k3=0,k1k2k3= 2pqr ＞0，若三个根全为实根，则必须一正两负，若三个根为两共轭虚根k1,k2与一个实根k3，则k1k2＞0，故k3＞0.那么这个正数k 是存在的.故时取最大值k.

综合以上情形，我们得出下面结论.

定理1设p,q,r 是不全为零的三个非负数，k 是一元三次方程k3- ( p2+ q2+ r2)k - 2pqr = 0 的正根，则对任意不全为零的实数x,y,z，恒有x2+ y2+ z2≥(2pyz + 2qxz + 2rxy)，仅 当x:y:z =时等号成立.

特例1当p ＞0,q = r = 0 时，可知k = p，仅当x:y:z = 0:1:1 时取最大值p.

特例2当p,q ＞0,r = 0 时，可知k =，仅当x:y:z = q:p:时取最大值为

特例3当p ＞0,q = r ＞0 时，方程k3- ( p2+ q2+ r2)k - 2pqr = 0 变为k3-( p2+ 2q2)k -2pq2=0，即(k + p)(k2- pk - 2q2) = 0，其唯一正根为，故仅当x:y:z =:1:1 时取最大值

特例4当p = 7,q = 19,r = 25 时，方程k3- ( p2+ q2+ r2)k - 2pqr = 0 为k3- 1035k - 6650=0，解得k = 35，即知当的最大值为35.

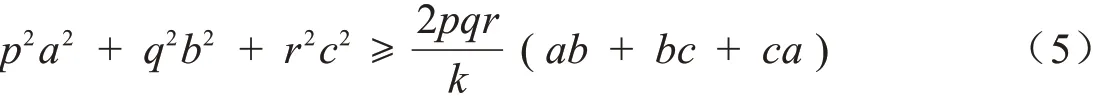
对三角形ABC，我们在（4）式中令a = cotA,b = cotB,c = cotC，由于cotAcotB + cotBcotC +cotCcotA = 1，即可得一个三角不等式.

定理2 若p,q,r 均大于零，k 是一元三次方程k3- ( p2+ q2+ r2)k - 2pqr = 0 的正根.则对任意三角形ABC，恒成立