基于NND-PCASVDD的多模态工业过程故障检测
刘文静, 谢彦红, 李 元
(1.沈阳化工大学 信息工程学院, 辽宁 沈阳 110142; 2.沈阳化工大学 数理系, 辽宁 沈阳 110142)
多变量统计过程控制已被广泛应用于过程监控领域[1-5].以上的拓展和改进算法相对传统的监控方法提高了故障检测效果,但都只考虑工业过程的线性和非线性情况,或是高斯和非高斯情况.现代工业生产是一个复杂的过程,实际的工业过程不仅存在线性和非线性,还存在高斯和非高斯混合的问题.
Tax等人提出支持向量数据描述(SVDD)方法[6],该方法是建立在支持向量机(SVM)思想的基础上,有非常强的单类数据处理能力.该算法可以很好地处理过程混合信息且不受非高斯和非线性的限制.随着研究的深入,学者们逐渐将该方法应用于过程监控领域[7-11].虽然SVDD方法有许多优点,但是从SVDD的算法可以看出,SVDD是一个最优规划的问题,在求解过程中需用核函数来进行数据计算.随着样本个数的增加,算法的计算量会呈现指数增长.如此,当需要计算的数据很庞大时就会产生维数灾难.为克服这一缺点,可以考虑降低样本集样本数或维数.Lin[12]等提出简化SVM的算法,但该算法对单分类的SVDD算法不太实用.Kim[13]等提出基于K值聚类局部支持向量的SVDD学习模型,但是K值的选择有待进一步讨论.近年来基于PCA降维的SVDD方法逐渐发展起来.戚元华[14]等将PCASVDD方法应用于天然气管道泄漏的检测中,实现对天然气管道泄漏的可靠检测.李冠男[15]等将PCASVDD方法应用于冷水机组的故障检测中,获得较高的冷水机组故障检测效率.Wang[16]等将PCASVDD方法应用于多级间歇故障监测过程,避免硬划分和分类错误的问题.PCASVDD算法对以上单模态过程故障检测取得了较好的检测结果.但是,随着市场经济的发展,为了增加企业的竞争优势、改变产品策略、提高质量,生产过程运行多种模态.通常情况下,PCASVDD故障检测算法是前期利用Z-SCORE 方法处理数据,然后在主元空间应用SVDD算法进行故障检测.由于Z-SCORE算法的影响,前期数据处理阶段不能剔除数据的多模态结构,导致主元空间数据仍然保持多模态结构.当故障发生在模态之间时,故障检测结果并不理想.为了解决这一问题,本文提出一种名为NND-PCASVDD的多模态过程故障的检测方法.该方法在前期数据处理阶段即可剔除多模态结构,保证过程变量服从单峰分布,为后面SVDD进行故障检测提供良好的数据基础.
1 主元分析
主元分析[17]将多变量数据从高维空间投影到反映数据变化方向的各个方差方向上,取其中方差较大部分作为主元部分,舍去较小部分以达到降维目的,它能够用较少的变量来表征原始数据多变量特征信息.其工作原理如下:
X∈Rn×m代表原始数据,n个样本,m个变量.通常情况下需要先对X作Z-SCORE标准化处理,之后对X作正交变换,将X分解为主元重构子空间和残差子空间.
(1)
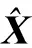
2 支持向量数据描述
支持数据向量描述[6-7](Support Vector data description,SVDD)的基本思想是数据集X={xi,i=1,2,…,N},通过某种非线性函数Φ:X→F将原始空间的数据投射到高维特征空间{Φ(xi),i=1,…,N},在高维征空间中找到一个几乎包含所有数据样本的最小体积超球体.a是超球体的球心,R1是超球体的半径.考虑到测量误差或者噪音等干扰引起的离群点影响,引入松弛变量ζi;C是惩罚参数.此问题可描述为:
s.t.‖Φ(xi)-a‖2≤
R12+ζi,ζi≥0
(2)
上述问题可转化为解决相应的对偶问题:
(3)
其中α是拉格朗日因子.
用核函数K(xi,xj)代替内积〈Φ(xi)·Φ(xj)〉可以将低维空间的数据向高维空间进行投射:
(4)
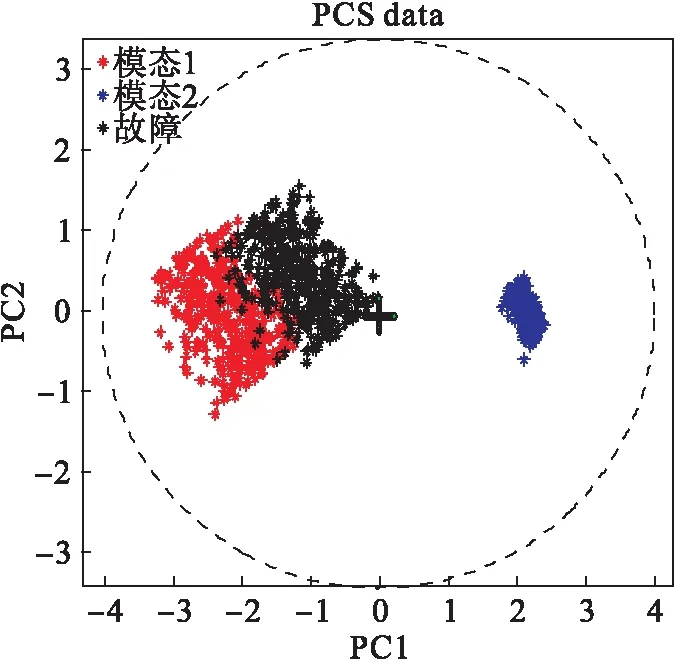
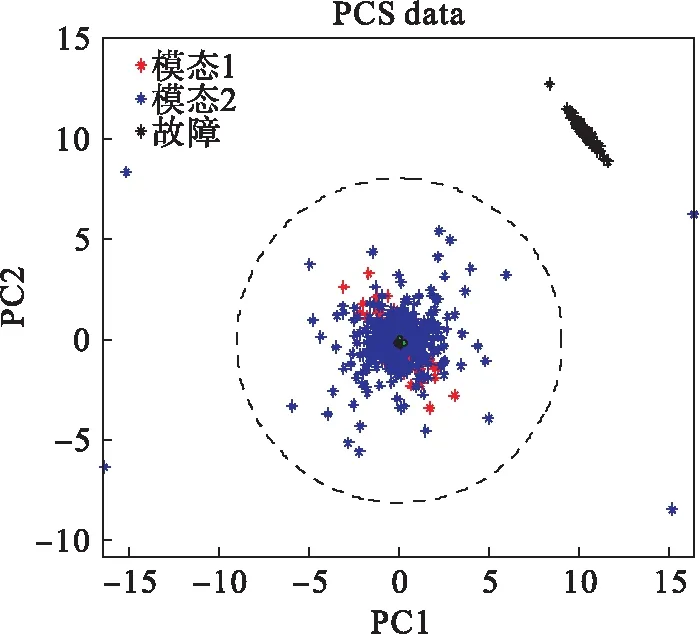
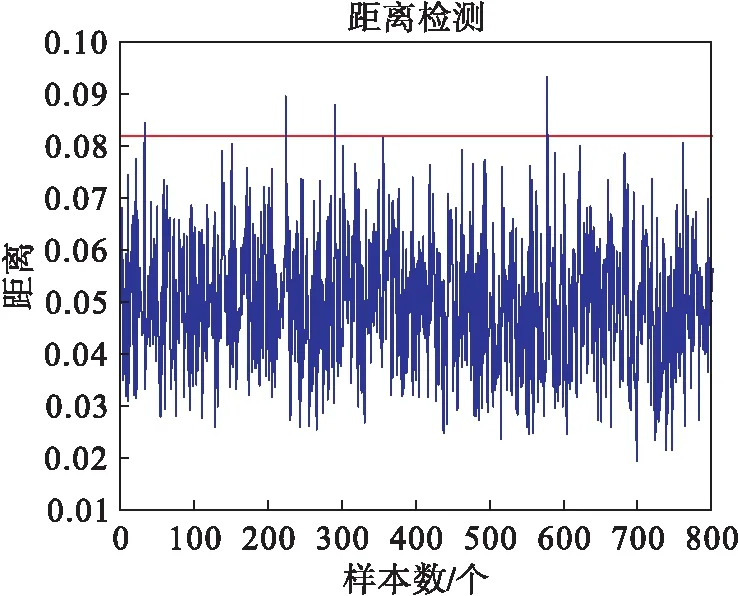
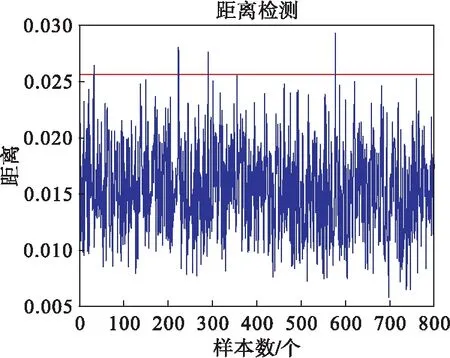
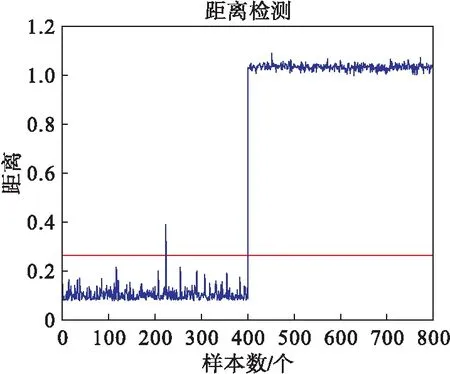
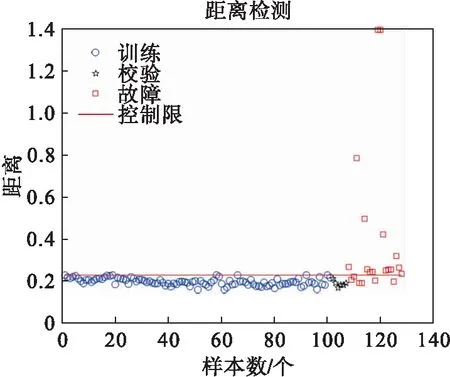
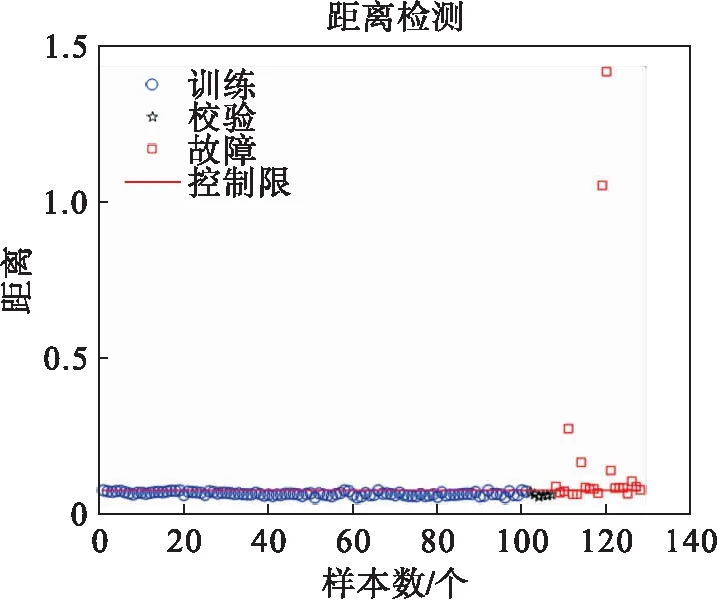
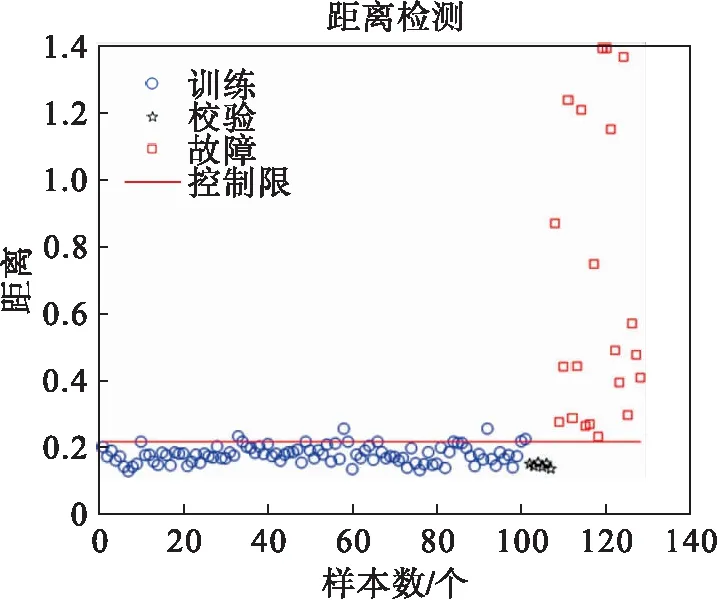
利用规划问题求解可以求出αi,如果0<αi (5) 对于新的样本xnew,其到超球体球心的距离可表示为: (6) 如果Dnew (7) 算法的检测流程如图1所示. 图1 算法流程Fig.1 Modeling and testing flow chart (3) 在差分集中应用PCA进行数据降维; (4) 对降维之后的差分样本集通过公式(5)计算超球半径R1. 对于一个新的测试样本xnew: Ge[19]等提出了一个典型的多模态模型,很多学者用此模型检测算法对复杂数据的有效性.为证明NND-PCASVDD方法的有效性,本文采用此模型来检测NND-PCASVDD算法的效果,模型结构如公式(8)所示. (8) 模型包括5个变量x1、x2、x3、x4和x5.s1和s2是潜在变量;e1、e2、e3、e4和e5是5个相互独立的噪声,均服从均值为0、标准差为0.01的高斯分布.两个设计的模态如公式(9)所示. 模态1s1uniform(-10,7) s2N(-15,1) 模态2s1uniform(2,5) s2N(7,1) (9) 两种模态下分别产生400个样本组成正常训练样本集.两个测试样本集由公式(9)产生.设定以下故障:系统运行在模态1下,T=401时刻起给x5加一个幅值为4的阶跃信号. 选取前2个变量方向作为主元方向.Z-SCORE标准化多模态数据不能剔除主元空间数据的多模态结构,而NND方法能够剔除主元空间数据的多模态结构. 图2、 图3展示了这两种算法的处理效果(PC1为第一主元,PC2为第二主元,虚线表示圆).图4、图5、图6为3种方法对故障的检测结果. 通过检测图可以看出当阶跃故障发生在两个模态之间时,SVDD方法及PCASVDD几乎不能检测出故障.这是因为SVDD及PCASVDD前期都是利用Z-SCORE方法处理数据,由图2可以清楚地看出当故障发生在两个模态之间时,Z-SCORE方法不能剔除主元空间数据多模态结构,导致SVDD在检测故障时将故障数据当做正常数据包在球内.NND剔除多模态同时将正常数据与故障数据分离,SVDD前期能够利用正常数据建立适当的模型,后期进行有效地故障检测. 图2 Z-SCORE处理后主元空间Fig.2 Principal component space after Z-SCORE processing 图3 NND差分后主元空间数据Fig.3 Principal component space after NND difference 图4 SVDD检测结果Fig.4 SVDD detection results 图5 PCASVDD检测结果Fig.5 PCASVDD detection results 图6 NND-PCASVDD检测结果Fig.6 NND-PCASVDD detection results 本文所应用的半导体数据[20-21]来源于美国德州仪器公司的半导体生产过程实际数据.选取17个过程变量用于故障检测方法对比的仿真实验.选取101个正常批次来建模,其中正常校验批次为6个,故障批次为21个.每个批次是不等长的,持续时间在95~112 s之间变化. 解决间歇过程批次不等长问题,传统的统计分析方法通常都是采用最短长度法.这种方法简单,但使数据轨迹的过程信息大量丢失,并且使点对点数据的相关性降低,导致此数据的可靠性降低.为了提高不等长间歇过程故障诊断的性能,本文采用统计模量分析算法对多模态数据进行预处理[22],所有的统计特征将会组合成一个(1×2m)维的特征向量,然后对统计模量进行差分运算. 图7、图8、图9为3种方法对27批数据的检测结果(6批检验,21批故障),可以看出SVDD及PCASVDD并没有将所有的故障检测出来.这是因为利用Z-SCORE没能剔除数据的多模态结构,无法保证SVDD建立适当的模型.因此,不能继续利用Z-SCORE处理多模态数据. 图7 SVDD检测结果Fig.7 SVDD detection results 图8 PCASVDD检测结果Fig.8 PCASVDD detection results 图9 NND-PCSVDD检测结果Fig.9 NND-PCASVDD detection results 针对PCASVDD方法对工业过程运行的多模态故障检测效果不理想的问题,本文分析了正常数据与故障数据的空间分布,提出基于NND-PCASVDD的多模态工业过程故障检测方法.运用近邻差分方法对数据进行预处理,剔除由于中心不同而存在的多模态形式.应用PCA方法对差分后的单模态数据进行特征提取,解决大样本情况下的计算复杂度问题.通过仿真实验证明了NND-PCASVDD方法的有效性及可行性.本方法继承了PCASVDD降低计算复杂度的优点;同时通过NND预处理技术解决了传统SVDD及PCASVDD对多模态过程故障检测效果不佳的问题,提高生产过程的可靠性.3 最近邻差分主元分析支持向量数据描述算法(NND-PCASVDD)
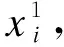
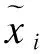
4 NND-PCASVDD算法多模态故障检测
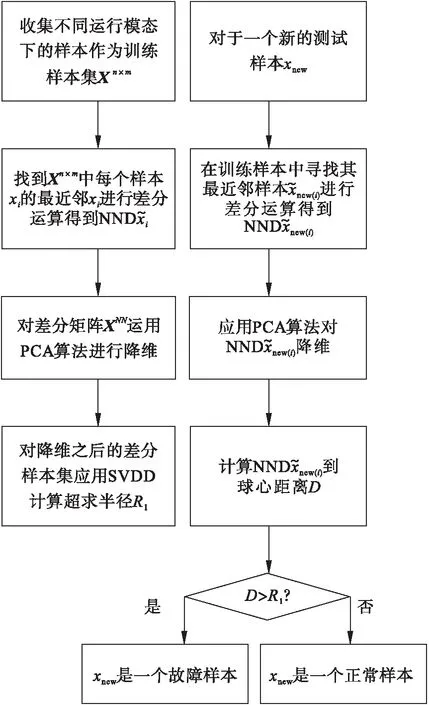
4.1 建模阶段
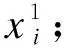
4.2 故障检测
5 仿真研究
5.1 数值例子
5.2 半导体生产过程
6 结 论

