基于小波分析-最小二乘支持向量机的转子碰摩故障诊断

金志浩， 于宝刚， 杨铮鑫， 王 雷

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

转子碰摩故障作为严重威胁旋转机械的常见故障，国内外学者对其进行了深入研究.Sinha等[1]发现转子叶轮受到冲击载荷时转轴会受到扭矩和轴向力的影响，转子系统失稳，从而发生碰摩.Ahmad[2]认为碰摩现象高度非线性，并发现混沌现象中含有包括碰摩信息在内的重要故障信息.He等[3]利用波束形成法和小波包能量法对碰摩声发射信号进行分析，可以准确判断转子碰摩位置.郑近德等[4]提出自适应部分经验模态分解法对碰摩信号进行分析，能够有效识别碰摩故障.当前主要有两大类方法应用于转子系统碰摩故障诊断：一类是基于故障理论模型的诊断方法;一类是基于故障信号的诊断方法[5].

基于信号的诊断方法具有快速性、实时性和高准确性等优点.相对于振动检测，声发射技术对旋转机械早期损伤更为敏感[6-7].对于碰摩声发射信号的研究主要集中在时频分析、神经网络等方面[8-10].小波分析可以同时使时间窗和频率窗发生改变，同傅里叶变换相比，其可以同时在时域和频域对信号进行分析，具有良好的时频分析特性[11].最小二乘支持向量机是标准向量机的一种扩展，在降低计算复杂性、加快算法收敛速度的同时[12-13]，较好地解决了小样本、非线性、高维数和局部极小点等实际问题，克服了在神经网络方法中无法避免的局部极值、过度学习等问题，具有很强的泛化能力[14-15].

FV520B 作为一种马氏体沉淀硬化不锈钢，其耐腐蚀性好、强度高、硬度高并且焊接性能良好，能够较好地满足转子系统对材料的要求，广泛应用于大型旋转机械的转轴和叶轮的生产中[16]，但是少有人对它的碰摩声发射信号进行分析.本文提出一种小波分析和最小二乘支持向量机相结合的方法(WA-LSSVM)来进行FV520B转子多碰摩副碰摩故障诊断.

1 小波变换及最小二乘支持向量机基本原理

1.1 小波变换基本原理

在函数空间L2(R)中，若ψ(ω)∈L2(R)的连续，其小波函数的容许性条件为：

(1)

式中：Ψ(ω)为ψ(t)的傅里叶变换，则将ψ(t)称作基本小波.将ψ(t)经过伸缩与平移后，得到一组小波基函数ψa,b(t)：

a,b∈R,a≠0

(2)

式中：a为尺度因子；b为平移因子.

将下式定义为关于小波基ψ的连续小波函数：

(Wψf)(a,b)=〈f,Ψa,b〉=

(3)

令连续小波变换中的尺度因子参数a=2-j，平移因子b=k2-j，其中j∈Z，k∈Z，则离散小波的定义为：

Cj,k=〈f,ψj,k〉=

(4)

式中C为与信号无关的常数.

1.2 最小二乘支持向量机(LSSVM)基本原理

最小二乘支持向量机回归的算法[17]，如下：

(1) 设已知训练集T={(x1,y1),…，(xn,yn)}∈(X×Y)n，其中：xi∈X=Rn，yi∈Y=R，i=1,2,3，……，n；

(2) 选择适当的参数与适合的核函数；

(3) 构造并求下列问题：

(5)

s.t.yi=WTφ(xi)+b+ei，i=1,2,3,…，n

其中：φ(•)为空间映射函数；w为权矢量；ei为误差变量；b为偏差量；j(•)为损失函数；γ为误差惩罚参数.

可构造拉格朗日函数：

L(w,b,e,α)=J(w,e)-

(6)

式中：αi∈R为拉格朗日乘子.分别求(6)式对ei，αi，w，b的偏导，联立可得：

(7)

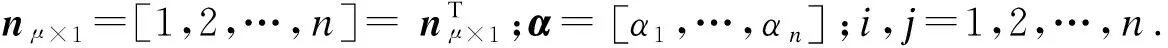
(4) 构造决策函数：

(8)

其中φ(x)Tφ(xi)为核函数部分.

2 小波分析和最小二乘支持向量机(WA-LSSVM)相结合的故障识别分类方法

利用小波分解进行声发射信号特征提取及应用LSSVM故障识别分类的模型如图1所示，具体步骤如下：

(1) 首先采用db10小波基对获取的声发射信号进行尺度为5的小波分解和细节重构.

(2) 对分解重构后的细节信号进行分析，假设原始信号中5个尺度层分别为1、2、3、4、5，则总信号S可以表示为：

S=S1+S2+S3+S4+S5

(9)

(3) 提取频带信号能量，设Si(i=1,2,3,4,5)对应的能量为Ei(i=1,2,3,4,5)，则有：

(10)

(4) 构造特征向量，以各尺度的能量为元素构造能量特征向量T，构造如下：

T=[E1，E2，E3，E4，E5]

(11)

当能量较大时，Ei(i=1,2,3,4,5)是一个较大的数值，不便于对数据进行处理，对此特征向量T进行归一化处理，令：

(12)

T′=[E1/E,E2/E,E3/E,E4/E,E5/E]

(13)

T′为归一化后的特征向量.

(5) 最小二乘支持向量机采用径向基函数作为核函数：

k(x,xi)=φ(x)Tφ(xi)=

exp[(-‖x-xi‖)/2σ2]

(14)

采用径向基核函数得到的最小二乘支持向量机的最优分类函数为：

(15)

从式(7)和式(14)可以看出：只有误差惩罚参数γ和径向基函数的宽度参数σ是待选的，本文采用交叉验证的方法选择误差惩罚参数γ和径向基函数的宽度参数σ.

(6) 分别取18组无碰摩、HT250定子与FV520B转子碰摩、15MnV定子与FV520B转子碰摩归一化后的特征向量作为LSSVM训练集，并且交叉验证，确定参数误差惩罚参数γ和径向基函数的宽度参数σ，再在上述工况分别取12组归一化后的特征向量作为LSSVM的测试集，进行不同材料的碰摩故障识别.

图1 声发射信号WA-LSSVM碰摩故障诊断模型Fig.1 Acoustic emission signal WA-LSSVM rubbing fault diagnosis model

3 实验研究

3.1 实验装置

实验采用转子试验台进行实验，利用碰摩试件和转盘碰摩来模拟旋转机械碰摩故障.该试验台用交流电机驱动，电机的转速由调速器进行控制.转子碰摩试验台如图2所示.图中1、2、3为基座，4为转轴，5为联轴器，6为转盘(材料为FV520B)，7为电机，在8、9、10位置分别安装1、2、3号传感器；声发射仪采用北京声华兴业公司的SDAEA声发射检测仪，传感器型号为SR150A；设采样频率为2 500 kHz、采样点数为2 048、采样时间为0.8 ms.

图2 转子碰摩试验台Fig.2 Rotor rubbing test bench

3.2 实验过程

HT250和15MnV是大型离心压缩机的常用壳体材料，因此研究FV520B转子与上述两种材料的碰摩极具现实意义.故实验过程中选取的碰摩试件材料为HT250和15MnV，碰摩试件的几何形状与尺寸完全相同.根据碰摩副的不同将实验分为A、B、C三组：A组为无碰摩故障实验；B组为HT250试件碰摩实验；C组为15MnV试件碰摩实验.实验过程中发现，在转速达到350 r/min、470 r/min、550 r/min、650 r/min、800 r/min和1 000 r/min时使试验台发生碰摩现象，能够听到明显的嗡鸣声.获得碰摩转速下各个工况的声发射信号，以350 r/min时C组碰摩实验为例，如图3所示.

图3 350 r/min时C组碰摩副碰摩的声发射信号Fig.3 Acoustic emission signals of group C rubbing pairs at 350 r/min

3.3 小波分析

选取上述实验过程中采集的无碰摩故障以及2种碰摩副在6种不同转速、工况下的声发射信号各30组.采用db10小波基对采集的540组声发射信号进行尺度为5的小波分解和细节重构，计算出各个尺度的能量比值.本文以转子转速为350 r/min时为例进行分析，如图4～图6所示.

图4 350 r/min摩多尺度能量百分比Fig.4 Multi-scale energy percentage without rubbing at 350 r/min

图5 350 r/min时HT250试件碰摩多尺度能量百分比Fig.5 Multi-scale energy percentage of HT250 specimen rubbing at 350 r/min

图6 350 r/min时15MnV试件碰摩多尺度能量百分比Fig.6 Multi-scale energy percentage of rubbing 15MnV specimen rubbing at 350 r/min

图4、图5、图6分别对应350 r/min时A组、B组、C组声发射信号小波分解后的各个尺度能量比值.由图4可知：在350 r/min的转速下，无碰摩时监测到的声发射信号所携带的能量主要集中在d3、d4、d5三个区域；图5和图6有碰摩试块时监测的信号所携带的能量主要集中在d2、d3两个区域.由多尺度能量百分比可以清楚分辨试件是否碰摩，但是对于何种材料碰摩，多尺度能量百分比仍不能准确判断，需做进一步研究.当转速为470 r/min、550 r/min、650 r/min、800 r/min和1 000 r/min时，分析情况与350 r/min类似，不再赘述.

3.4 最小二乘支持向量机碰摩故障诊断识别

LSSVM是处理二分类问题的方法，但在实际应用中需要解决多分类问题[18]，现在多类分类算法有一对一、一对多和有向决策树分类法等.本文需要对3种不同工况进行分类，应用一对多分类算法.将实验所采集的声发射信号经小波分解后得到的各尺度能量百分比作为LSSVM分类器的输入.以转子350 r/min时为例，将声发射信号在3种不同工况下小波分解的能量百分比各随机取18组作为训练样本，交叉验证，最后确定误差惩罚参数为0.1、径向基函数的宽度参数为100；剩余12组作为测试样本，应用LSSVM分类器进行碰摩故障识别分类.设无碰摩时分类器输出为1，HT250试件碰摩时分类器输出为2， 15MnV试件碰摩时分类器输出为3. 当转速为470 r/min、550 r/min、650 r/min、800 r/min和1 000 r/min时，分析步骤与350 r/min相同.分类结果如图7～图12所示.

由图7～图12和表1可知：FV520B转子声发射信号通过WA-LSSVM方法进行分析，可以高效的对碰摩故障进行诊断，并且能够识别不同的碰摩材料，准确率均达到83 %以上.因此，小波分析和最小二乘支持向量机相结合的方法能够快速有效地诊断转子碰摩故障，并且识别碰摩材料.

图7 350 r/min时故障诊断识别结果Fig.7 Fault diagnosis identification results at 350 r/min

图8 470 r/min时故障诊断识别结果Fig.8 Fault diagnosis identification results at 470 r/min

图9 550 r/min时故障诊断识别结果Fig.9 Fault diagnosis identification results at 550 r/min

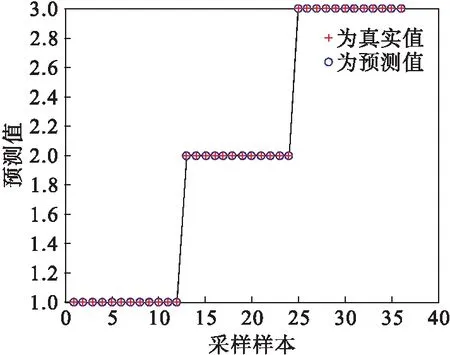
图10 650 r/min时故障诊断识别结果Fig.10 Fault diagnosis identification results at 650 r/min

图11 800 r/min时故障诊断识别结果Fig.11 Fault diagnosis identification results at 800 r/min

图12 1 000 r/min时故障诊断识别结果Fig.12 Fault diagnosis identification results at 1 000 r/min

表1 WA-LSSVM诊断模型对测试样本的识别正确率

4 结 论

利用小波多尺度分解获取FV520B转子声发射信号的各尺度能量百分比，并将能量百分比作为最小二乘支持向量机分类器的输入，得到以下结论：

(1) 转子声发射信号通过小波多尺度分解，发现无碰摩时，声发射信号能量主要集中在d3、d4、d5三个区域；发生碰摩时，能量主要集中在d2、d3两个区域.通过分析各尺度的能量百分比，可以直观有效的对转子碰摩故障进行诊断.

(2) 提出基于小波分析和最小二乘支持向量机的转子碰摩故障诊断方法，开展碰摩故障诊断测试实验，结果表明该方法能够快速高效的对FV520转子碰摩进行诊断，并且对碰摩材料进行识别，识别准确度均大于83 %.

(3) 实验采用了两种材料与FV520B转子碰摩，为实际工程中采用其他材料的碰摩故障诊断提供技术支持.