混合传感器网络在WSN栅栏覆盖的优化研究

王 军， 赵子君

(沈阳化工大学 计算机科学与技术学院， 辽宁 沈阳 110142)

随着科学技术的发展和无线传感器网络(wireless sensor networks,WSNs)的普及应用，无线传感器网络在我们的生活中扮演着越来越重要的角色[1].无线传感器网络栅栏覆盖技术不仅应用在海上监测、海洋污染、森林火灾等自然灾害方面，而且在军事、国防安全等方面具有广泛的应用价值[2]，能有效侦测入侵目标.通过在监测区域内投放大量的静态无线传感器节点可获取实时信息，但是由于节点投放的随机性导致监测区域的覆盖不均匀，无法形成有效的栅栏覆盖，因此，设计一种移动节点调度优化方案以提高栅栏覆盖质量至关重要.

目前，对传统无线传感器网络中的栅栏覆盖问题已经进行了很多研究.1992年，Gage等人定义了栅栏覆盖，并使移动目标穿越栅栏时不被发现的概率最低[3]；2007年Kumar等人对栅栏进行了强弱的区别，提出了强K重栅栏覆盖和弱K重栅栏覆盖，并且研究了其形成栅栏时所需的最少节点数和相关参数[4]；2009年，Saipulla等人研究了混合无线传感器网络通过节点移动判断存在栅栏覆盖的算法[5].

本文研究由固定节点和移动节点共同组成混合无线传感器网络栅栏覆盖，通过添加移动节点，实现目标区域的1-栅栏覆盖，优化无线传感器网络栅栏覆盖策略，有效地对移动目标进行检测.

1 相关问题

1.1 栅栏覆盖

栅栏覆盖(barrier coverage)是利用无线传感器网络节点布置在狭长区域形成,用于监测是否有入侵目标穿越覆盖区域的一种无线传感器网络覆盖问题[6].

Meguerdichian等人提出最好情形和最坏情形的栅栏覆盖控制算法[7-8]，算法依据Voronoi图与Delaunay三角网为理论基础.如图1所示，如果某入侵目标沿着Voronoi图的边穿越网络时，即沿着实线的SD路径入侵时，由于路径上的每个点所在的位置与最近节点所在位置的距离最大，因此，被监测到的概率最小，该路径被称为“最大突破路径(maximal breach path)”，由Voronoi 图中的线段组成.对于侦察的一方，这样的路径就是“最坏情形的路径”；如果路径上的每个点所在的位置与最近节点所在位置的距离最小，则称该路径为“最大支撑路径(maximal support path)”.即当目标沿着由Delaunay三角网中的线段穿越网络时，即沿着虚线SD路径入侵时，被检测到的概率最大，因此，对于监测方，这样的路径就是“最好情形路径”.

图1 最好情形和最坏情形的栅栏覆盖Fig.1 The best and worst case of the barrier coverage

1.2 蚁群算法

蚁群算法(Ant Colony Optimization,ACO)是在20世纪90年代初期，意大利学者Colorni，Dorigo和Maniezzo等人，从蚂蚁寻找食物的行为中受到启发，通过模拟蚂蚁寻找食物的方式得出了一种群智能算法[9].当蚂蚁寻找食物时会在路径上留下一种外激素的化学物质，又叫信息素(pheromone).通过识别信息素的浓度，蚂蚁可以找到回到巢穴的最优路径，而且不会迷路.蚂蚁选择信息素浓度较高的方向，从而形成了正反馈机制，使得该方法易于发现较好解.蚁群算法还有许多优点，它具有较强的鲁棒性，易于和其他算法结合，所以，在现实生活中诸多方面均有应用[10].

1.3 Delaunay图

Delaunay图即对于一组无线传感器固定节点，可以得到很多种不用的三角剖分，其中最优三角剖分就是Delaunay三角网[11].其最重要的两个性质体现在：唯一性，一组点无论如何构造都能得到同一个Delaunay三角网；不相交性，Delaunay三角网内各边都不相交.

1.4 Voronoi图

Voronoi 图亦称泰森多边形，与Delaunay三角剖分是对偶关系,是一组由连接两个相邻点的直线的垂直平分线组成的连续多边形，平面由节点集划分成多个多边形区域，而且每个区域只包括节点集中的一个节点[12].Voronoi 图可以应用于栅栏覆盖中.根据Voronoi 图可以直观地观察出栅栏覆盖的目标穿越路径，如图2所示.

图2 移动目标穿越路径Fig.2 Moving target traversing path

2 基于D-ACO的覆盖优化策略

2.1 覆盖空洞的判断

在狭长的栅栏覆盖区域中，通过对各传感器节点和它所在的Voronoi区域所有边之间的距离d和节点感知半径Rs的大小比较，判断是否存在覆盖空洞[13].根据Voronoi图的性质，该距离d等于两个相邻节点Oa、Ob距离的一半.已知每个传感器节点都能获取自身位置信息以及Voronoi图中相邻节点的位置信息.其中，传感器节点到Voronoi 多边形边的距离用d表示，O表示传感器节点，则有

(1)

当d>Rs时一定存在覆盖漏洞，当dRs时一定不存在覆盖漏洞.通过比较距离与节点感知半径的大小关系可知节点的通信范围和所在Voronoi多边形之间可能存在以下3种位置关系：

(1)节点的感知范围即通信半径可能和Voronoi多边形的边有一个交点或多个交点，如图3所示，可能和其中一个边相交，此时距离d等于感知半径Rs；也可能和其中多个边相交，此时距离d小于感知半径Rs.

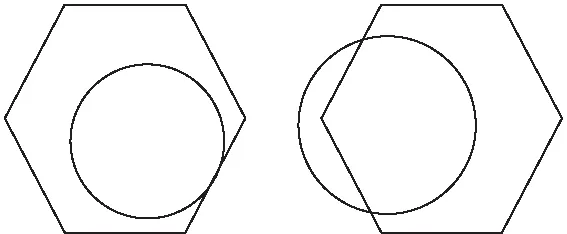
图3 一个或多个交点Fig.3 One or more intersection points

(2)Voronoi多边形可能完全包围节点的通信区域，此时距离d大于感知半径Rs；也可能完全被通信区域所覆盖，此时距离d小于感知半径Rs，如图4所示.

图4 包围或覆盖Fig.4 Enclosure or coverage

(3)当几个节点相邻时，传感器节点中心与Voronoi区域的边的距离d大于感知半径Rs时，则传感器节点之间一定存在覆盖空洞，如图5所示.

图5 一定存在覆盖空洞Fig.5 There must be an empty hole

2.2 蚁群算法的改进

在传统的蚁群算法中，蚂蚁在向着食物方向搜索的过程中会释放信息素，不过信息素的浓度是随着时间的增加而增加的，因此，蚂蚁在搜索初期的初始信息素匮乏，导致算法收敛速度慢，算法中后期，信息素浓度过高易陷入局部最优[14].

2.2.1 正向搜索

首先为蚁群设置搜索起点，即狭长区域最左侧的固定节点为搜索起点，相对于传统的蚁群算法，正向搜索是令蚁群从狭长区域的一端向另一端进行正向搜索，不可以反方向搜索.

2.2.2 根据Delaunay三角网最短边进行搜索

最初的蚁群算法是由于蚂蚁留下的信息素经过的时间越长剩余的就越少，蚂蚁在短路径上往返的时间较少，所以信息素还没挥发完，就有新的信息素产生.因此，短路径上的信息素浓度比长路径上的信息素浓度高，从而吸引更多蚂蚁选择短路径，然后又留下新的信息素，如此反复，整个蚁群最终聚集到最短路径上[15].而改进的蚁群算法是根据Delaunay三角网的最短边进行搜索，省去了很多选择路径的时间，提高了算法的搜索效率.由此根据Delaunay三角形边长判断是否需要填充移动节点，下面分3种情况进行讨论.

(1)当BC<2Rs时，即两个传感器节点的距离小于传感器节点的通信直径时(图6)，传感器节点间无覆盖空洞，不需要填充移动节点.

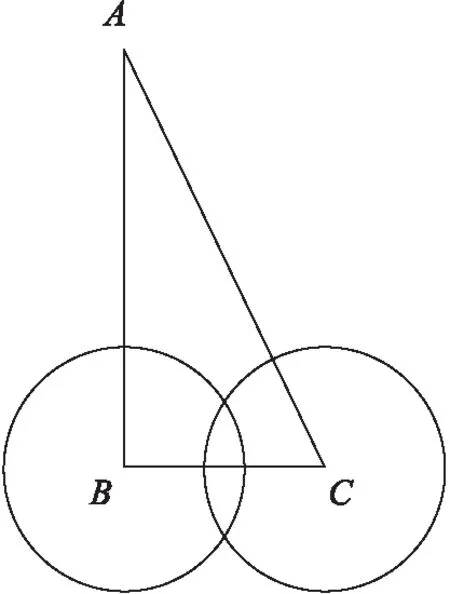
图6 BC<2RsFig.6 BC<2Rs

(2)当BC=2Rs时，即两个传感器节点的距离等于传感器节点的通信直径时(图7)，传感器节点间无覆盖空洞，不需要填充移动节点.

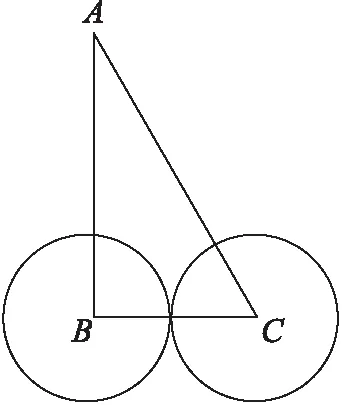
图7 BC=2RsFig.7 BC=2Rs

(3)当BC>2Rs时，即两个传感器节点的距离大于传感器节点的通信直径时(图8)，此时栅栏出现了覆盖漏洞，需要填充移动节点.

图8 BC>2RsFig.8 BC>2Rs

2.3 填充移动节点方法

根据改进的蚁群算法和Delaunay三角网的最短边进行正向搜索确定下来的栅栏覆盖路径，再利用蚁群算法以每2Rs为距离进行移动节点的填充，直到路径上没有未被覆盖的区域，最终形成栅栏覆盖.如图9所示.

图9 填充移动节点方法Fig.9 Filling mobile node method

2.4 算法执行过程

算法具体步骤如下：

步骤1：在目标区域A×B的狭长带状区域内随机部署固定节点，并且根据固定节点部署情况生成对应的Voronoi图.

步骤2：通过Voronoi图判断是否存在栅栏覆盖空洞，若存在，进行步骤3修复覆盖空洞；否则，此覆盖符合栅栏覆盖要求，退出算法.

步骤3：根据节点分布构建Delaunay三角网，再依据改进的蚁群算法，根据Delaunay三角网最短边进行正向搜索，得到的路径便是需要修复的栅栏覆盖路径.

步骤4：根据填充移动节点方法进行节点填充.

步骤5：再次构建Voronoi图判断是否存在栅栏覆盖空洞.若仍然存在，转到步骤3修复覆盖空洞，若不存在转到步骤6.

步骤6：记录移动节点的最终位置并生成最终的网络覆盖图.

3 仿 真

使用Matlab仿真软件进行仿真实验.构建网络模型为1 000 m×300 m的狭长带状仿真区域，初始条件下随机放置40个固定节点和两端固定位置的2个节点，左侧初始节点坐标为(0，150)，右侧最终节点坐标为(1 000，150)，生成对应的Voronoi图,如图10所示.经过Voronoi栅栏覆盖空洞检测后，运用本文算法，构建Delaunay三角网，利用蚁群算法修复栅栏覆盖漏洞，添加了11个移动节点，最终形成完整的1-栅栏覆盖，如图11所示.经过100组实验仿真分析，栅栏完全修复的误差低于10 %，证明算法可行.

图10 初始部署状态Fig.10 Initial deployment status

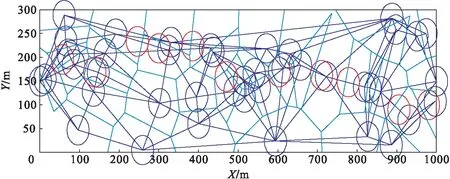
图11 优化后部署状态Fig.11 Optimized post deployment status

3.1 节点自身属性对算法的影响

当节点自身的属性变化时，会对移动节点添加数量产生影响.如图12所示，在一定大小的仿真区域内，节点的通信半径一定时，可以明显看出，固定节点数量越大，所需添加移动节点数量越少；当固定节点数量一定时，随着节点通信半径的增大，所需添加移动节点的个数逐渐变少.综上所述，随着固定节点数量的增加，当节点的通信半径增大时，所需添加移动节点个数逐渐变少，算法执行速度越快.

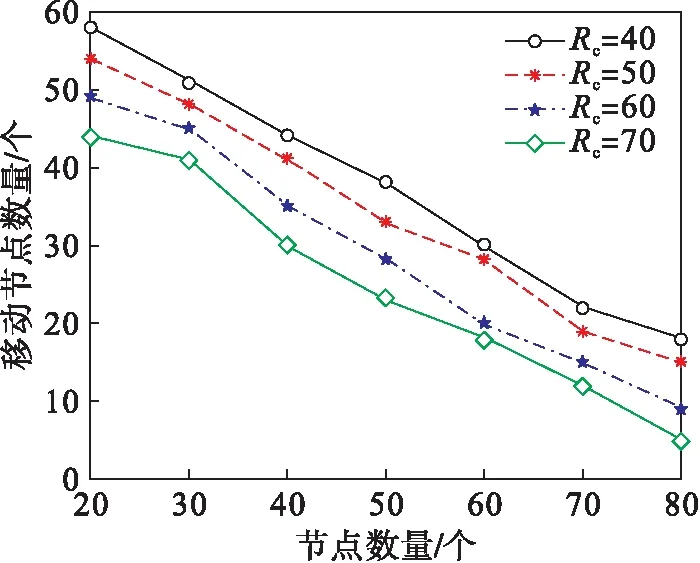
图12 节点数量和移动节点数量的关系Fig.12 The relationship between the number of nodes and the number of mobile nodes

3.2 不同算法的比较

为了更好地体现D-ACO算法的性能，现与其他的栅栏覆盖修复算法进行对比，分别是Voronoi算法[13]和CBGB算法[16].如图13所示，D-ACO算法执行速度和1-栅栏覆盖的形成效率明显优于Voronoi算法和CBGB算法.当节点数量是20时，Voronoi算法和CBGB算法所形成栅栏的长度均比D-ACO算法长；当节点数量为80时，3个算法形成的栅栏长度趋于相同.3个算法都是随着节点的增加，形成的栅栏长度越来越短，Voronoi算法和CBGB算法的优点在于固定节点冗余明显小于D-ACD算法.

图13 节点数量和栅栏长度的关系Fig.13 The relationship between the number of nodes and the length of the fence

4 结束语

栅栏覆盖问题是无线传感器网络中的基本问题.本文提出一种改进后的蚁群算法(D-ACO 算法)，用于混合无线传感器网络中指导移动节点的部署.通过仿真结果分析表明：D-ACO算法形成效率和栅栏长度明显优于其他算法，D-ACO算法优化了混合传感器网络的栅栏覆盖策略，能够有效地侦测入侵目标.本课题所研究的改进智能蚁群算法指导混合无线传感器网络中各个节点完成最初的规划部署位置后，移动节点需要改变自身位置，到达目标地点，在此过程中包括移动路径、节点能量消耗等问题.本课题组在对网络基本规划完成的基础上，需要进一步研究移动节点的路径寻优、能量分配方案等问题，完成传感器网络部署的整个过程.