EEMD与小波包在液压管道振动信号研究

张金萍， 王宇雁， 王婉莹

(沈阳化工大学 机械工程学院， 辽宁 沈阳 110142)

1998年美国工程院士Norden E.Huang提出一种谱分析方法即HHT变换[1-2]该方法主要由两部分构成：经验模态分解以及Hilbert谱.在液压系统故障诊断中EMD(经验模态分解)分解经常被用于非线性、非平稳信号的处理[3-4]，在实际的应用当中发现该方法具有很大的缺陷，尤其是存在模态混叠现象和端点效应.对分析结果有很大影响，直接影响最后结果的准确性，给故障的排查和分析增添许多麻烦[5-6].陈彦龙等[7]和臧怀刚等[8]分别采用DCT去噪和消除信号中噪声的方法然后再对信号进行EMD处理，得到的结果都是比单纯执行EMD效果更好.近年来针对EMD的改进方法有很多，例如时间序列模型处理、多项式的拟合以及EEMD等处理方式[9].这些方法都在一定程度上减小了模态混叠现象和端点效应，而小波变换在处理非平稳信号以及非周期信号方面有很好地应用，小波包是在傅里叶变换的基础上进行改进和提高，具有良好的时域局部化能力以及可以实现多分辨率等特点，非常适合用于非平稳信号的处理[10].但是小波包的小波基难以选择，近年来有学者提出将EEMD和Hilbert包络谱分析相结合的方法来对液压故障进行诊断[11-12].EEMD在对信号进行分解处理时会对IMF(本征模态函数)进行大量的迭代，而且各模态分量的频率也不是完全按照大小进行排列，所以会造成部分伪分量对最后的分析结果带来很大的影响.小波分析虽然提出时间较早，但其依然是应用数学领域的重要发展方向，在故障诊断领域中小波分析也取得了很好的效果.但其所具有的不足也依然凸出，最主要的一个因素就是人的因素,例如去噪时阀值的选择等因素[13].本文通过将小波包与Hilbert包络谱分析以及EEMD分解相结合的方式对信号进行分析，减小了仅用EEMD方法对信号进行分解时产生的模态混叠现象，通过实验分析证明该方法可以准确提取液压系统发生泄漏时的故障频率.

1 小波包分析

(1)

(1) 小波包分解算法

(2)

(2) 小波包重构算法

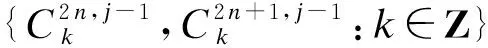
(3)

式中：{hk}k∈Z∈l2(Z)为低通滤波器系数；{gk}k∈Z∈l2(Z)为高通滤波器系数.

2 EEMD分解

EEMD方法的本质是添加高斯白噪声重复多次EMD分解[14].具体操作如下：

(1) 把将要处理的信号x(t)加入标准差为固定常数c、幅值为0的白噪声nq(t)，然后对信号进行归一处理得到xq(t).

(2) 将得到的信号xq(t)进行EMD分解.

(3) 多次重复上述两个步骤，每次都对信号加入随机生成的正态分布白噪声,得到本征模态函数IMF.

(4) 将(3)中所获得的众多IMF分量求平均值，将其作为x(t)固有的模态函数.

(4)

其中:q是分解时在原信号添加白噪声的次数;p表示信号为分解到第p阶的IMF分量.

3 相关性分析和Hilbert包络谱分析

3.1 相关性分析

在信号分析中经常需要对两个或两个以上信号之间的关系进行研究，常采用某一个量来表示出这些信号之间的相似程度.

(5)

该公式为互相关函数的定义式.

设两个信号x(t)、y(t)为能量信号，则x(t)、y(t)的互相关函数为:

(6)

如果两信号正交说明这两个信号没有关系.

3.2 Hilbert包络谱分析

设有信号x(t)经过Hilbert变换可以得到：

(7)

并求出x(t)的包络信号：

(8)

4 基于EEMD和小波包的方法

首先需要用小波包对原信号进行分解，去除干扰因素，将进行数据分析时所需要的信息进行保存.然后用EEMD将小波包重构之后的信号进行分解，引入数据相互关系数，以小波重构的信号作为参照，计算各阶IMF和小波包重构信号的相关系数，对相关性系数大的分量进行保留.将这些所保留的IMF进行组合得到新的分析信号，最后再对新的信号进行时频分析，从中筛选出故障频率特征.该方法的具体步骤为：

(1) 获得原始信号在确定小波基以及分解层数后，将原始信号利用小波包进行分解.

(2) 对小波包各个节点求方差和均值，以均值和方差之和为阀值，将绝对值小于阀值的分量设置为零，压缩小波系数.

(3) 重构信号把重新构造所得到的信号作为求互相关系系数的列向量.

(4) 用EEMD对已经重构的信号进行分解，将所得到的IMF分量作为第二个列向量，并求出IMF与重构信号之间的相关系数.

(5) 选择相关系数大的IMF进行Hilbert包络谱分析，筛选得到故障信息.

5 数据分析

引用的数据来自Case Western Reserve University Bearing Data Center提供的免费数据[15]，轴承类型为6205，内径25 mm，外径52 mm.数据采集频率48 000 Hz，故障频率162 Hz，选用Daubechies小波，并将原始信号分为8层，将原始信号分解完之后对小波包各个节点求取方差和均值后求和，并将信号进行重新构造，用EEMD对重构的信号进行分解，得到结果如图1所示，求出IMF与重构信号之间的相关系数如表1所示，其中IMF1、IMF2、 IMF5、IMF6这4个相关性比较大.最后选取这4个进行信号重组，对重组后的信号进行包络谱分析，其结果如图2所示.

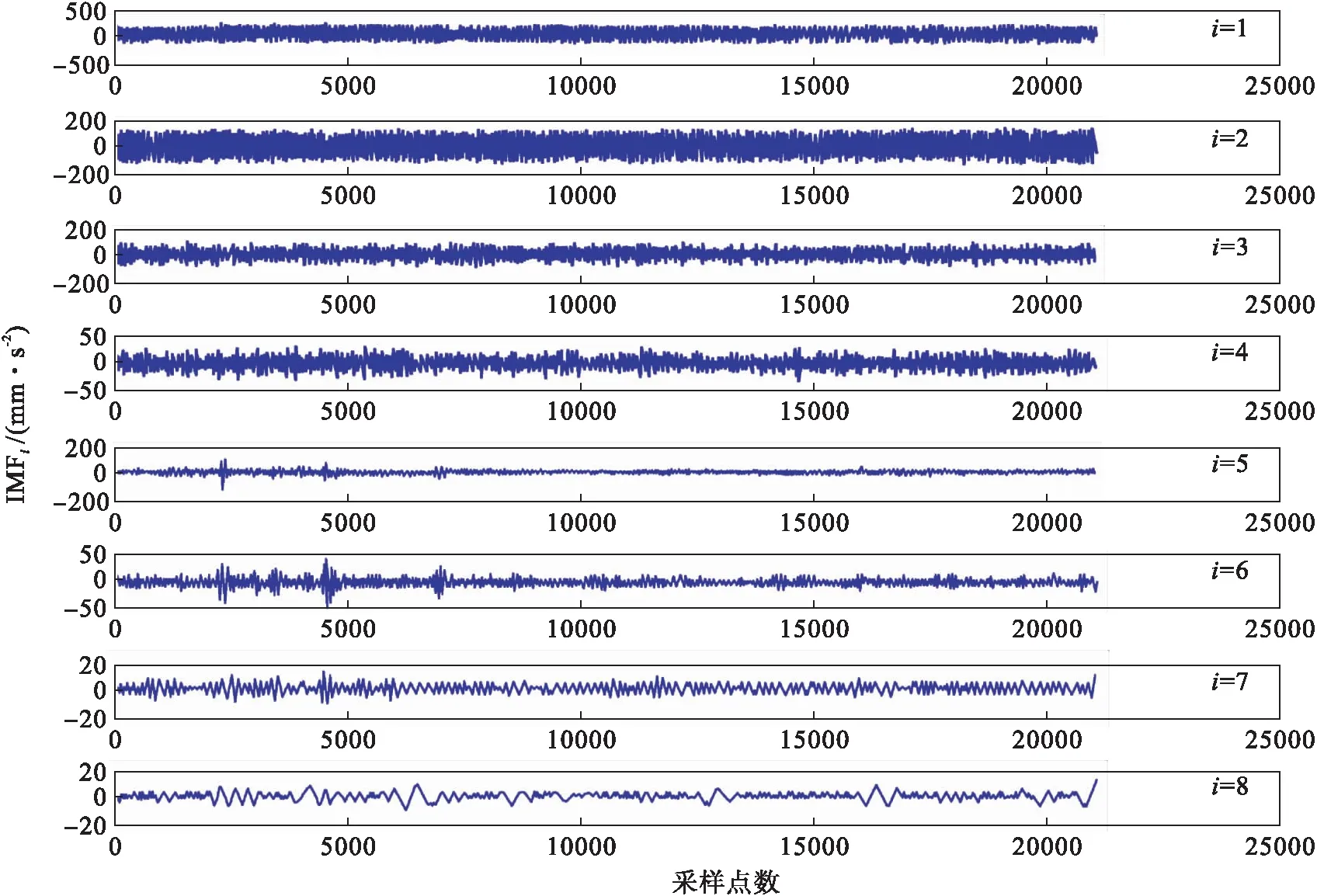
图1 轴承信号采样点数Fig.1 Sampling points of bearing signal

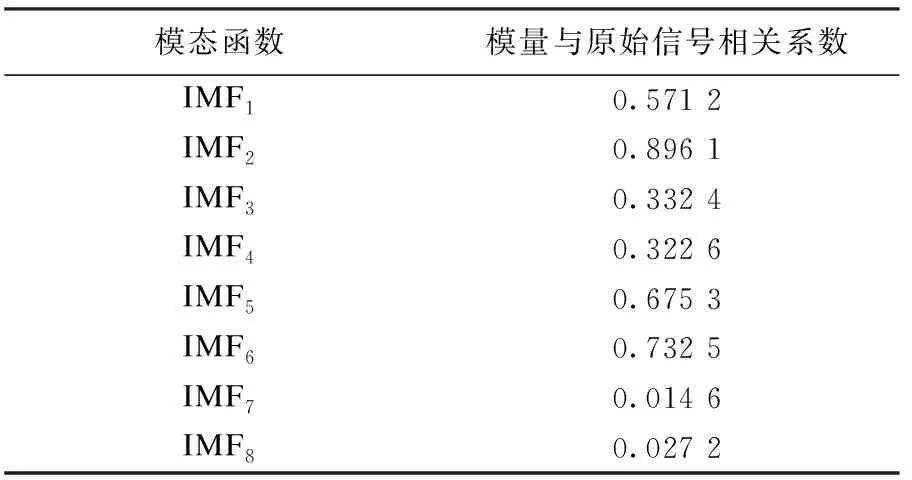
表1 轴承信号EEMD分量相关系数分析

图3是对原始信号直接进行EEMD分解之后选取前4个分量进行包络谱分析的结果.对比图2和图3可以发现：图2检测到故障信号频率在161.6 Hz，与真实故障频率的误差小于3 %，属于有效范围，图3检测到的故障频率在161.3 Hz，与真实故障频率的误差小于3 %，属于有效范围；图2当中干扰频率比较少，没有其他多余的频率，而图3当中有许多干扰频率；通过对比可知图2的诊断效果明显优于图3，表明该方法切实有效.

图2 轴承重组信号包络谱分析Fig.2 Envelope spectrum analysis of bearing recombination signal

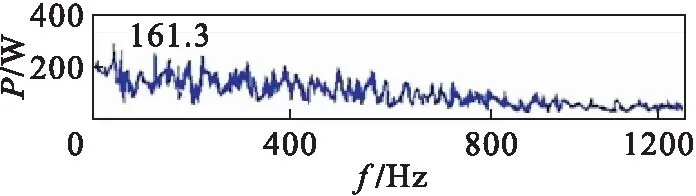
图3 轴承信号前4节之和包络谱分析Fig.3 Envelope spectrum analysis of the sum of the first four sections of bearing signal

6 实测数据分析

选取实际工况下管道振动信号进行实验分析.采集某压力机工作时液压管道发生泄漏的振动信号，采样频率为1 000 Hz，采样点数为6 700点.根据实际情况和经验可知管道故障频率为31.1 Hz，对原信号采用Daubechies小波进行分解降噪，将原始信号分为8层，分解完成之后用小波包各个节点求取方差和均值后求和，并将信号进行重新构造.用EEMD对重构的信号进行分解得到结果如图4所示，求出IMF与重构信号之间的相关系数如表2所示，其中IMF2、IMF3、IMF5和IMF6这4个本征模态函数的相关性系数较大，故选取IMF2、IMF3、 IMF5和IMF6相关系数大的分量进行信号重组，对重组后的信号进行包络谱分析，其结果如图5所示.

图4 液压信号采样点数Fig.4 Sampling points of hydraulic signal

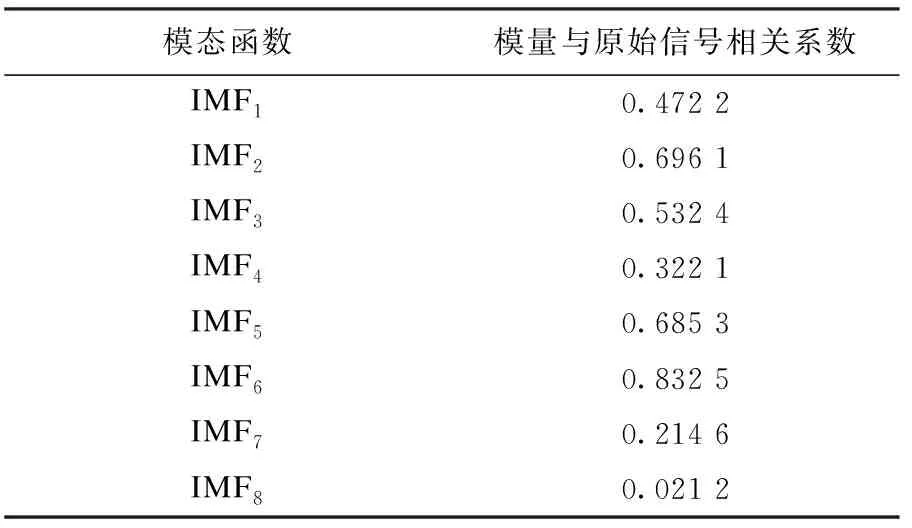
表2 液压信号EEMD分量相关系数分析

从图5可以看出:该压力机发生管道泄漏时的故障频率为30.2 Hz，与真实故障频率的误差小于3 %，属于有效范围，干扰频率较少，故障频率明显.

图5 液压重组信号包络谱分析Fig.5 Envelop spectrum analysis of hydraulic recombination signal

图6是对原始信号直接进行EEMD分解之后选取前 4 个分量进行包络谱分析的结果.其结果显示检测出故障频率为30.4 Hz，与真实故障频率的误差小于3 %，属于有效范围，在图中同时还包含其他干扰频率.对图5和图6进行对比可知：图5的诊断效果明显优于图6，表明该方法切实有效.

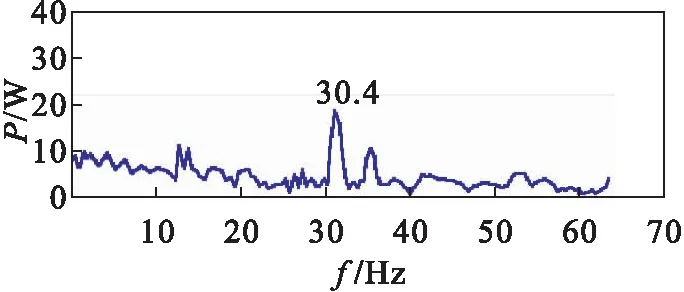
图6 液压信号EEMD分解前4节之和包络谱分析Fig.6 Envelope spectrum analysis of the sum of the first four sections of hydraulic signal

7 结 论

为得到更为准确的液压管道振动信号分别选取小波包分析与EEMD分解，并提出将两种方法与Hilbert包络谱分析相结合，用小波包对信号进行降噪并对信号进行重组，对液压系统的液压管道进行信号采集并对该信号进行分析.通过对液压管道持续信号的分析验证得出：采用小波包与EEMD相结合的方法可以准确得到故障频率并且干扰频率少，比直接采用EEMD分解效果好.