破片式ARM杀伤域分析及单发毁伤概率研究

张 毅，李 青，吴 鹏，周弘扬，殷 洁

(1.空军勤务学院， 江苏 徐州 221000； 2.中国人民解放军95903部队， 武汉 136200； 3.中国人民解放军94865部队， 杭州 310000)

空地反辐射导弹(Anti-Radiation Missile,ARM)作为压制防空系统的主要武器，是现代战争中压制和摧毁各类辐射源、夺取制电磁权和制空权的重要手段[1-2]。制导精度作为ARM的重要性能之一，直接影响导弹的杀伤概率。导弹的制导误差是影响制导精度的主要因素，分为系统误差和随机误差。系统误差是指实际弹道的平均弹道相对理想弹道的偏差，一般指导弹姿态误差、主子惯导对准误差、数据更新周期导致的误差等。随机误差是指实际弹道相对其平均弹道的偏差，一般用CEP描述随机误差[3-4]。

目前，进行破片式ARM单发毁伤概率分析时，对随机误差的研究较为成熟，例如，俞波通过建立随机误差数学模型，定量分析了其对激光末制导炮弹命中精度的影响[5]。对于系统误差影响研究，吴彤薇等通过分析系统误差合成、误差分配等方法对截获概率进行了仿真，王军等对导引头动态视场误差进行了分析，计算得到其捕获概率[6-7]。但对于系统误差影响单发毁伤概率的量化研究较少，而系统误差作为影响制导误差的重要环节，对导弹单发毁伤概率必然有着不可忽视的影响。本文针对此问题，通过建立破片式ARM单发毁伤概率计算模型，分析导弹无效杀伤区域，量化研究系统误差对破片式ARM单发毁伤概率的影响。

1 单发毁伤概率计算模型

1.1 参数与假设

为便于分析，本文在具体分析激光引信各项参数时，以PAC-2/3的制导雷达AN/MPQ-53为例进行具体分析，其参数为舱体长5 m、宽2.5 m、高2.6 m，雷达天线直径为2.4 m，馈源点高度为5 m。

在计算ARM单发毁伤概率时，假设使用“线阵推扫”方式进行探测；在激光引信探测区域内，导弹能够通过触发起爆或者近炸起爆的方式有效毁伤目标[8-11]。

对于ARM破片式战斗部，依据杀伤准则与目标易损特性[12]，可做出如下假设：每条随机弹道的导弹对目标的杀伤概率仅分为1和0两种情况，导弹直接命中天线板，杀伤概率为1；非直接命中天线板的情况下，若破片飞散中心命中天线板，杀伤概率为1，否则杀伤概率为0。

1.2 模型建立

在弹道平面内建立坐标系如图1所示，坐标原点O1为天线板几何中心在弹道平面上的投影，作为理想瞄准点，O2为实际瞄准点。

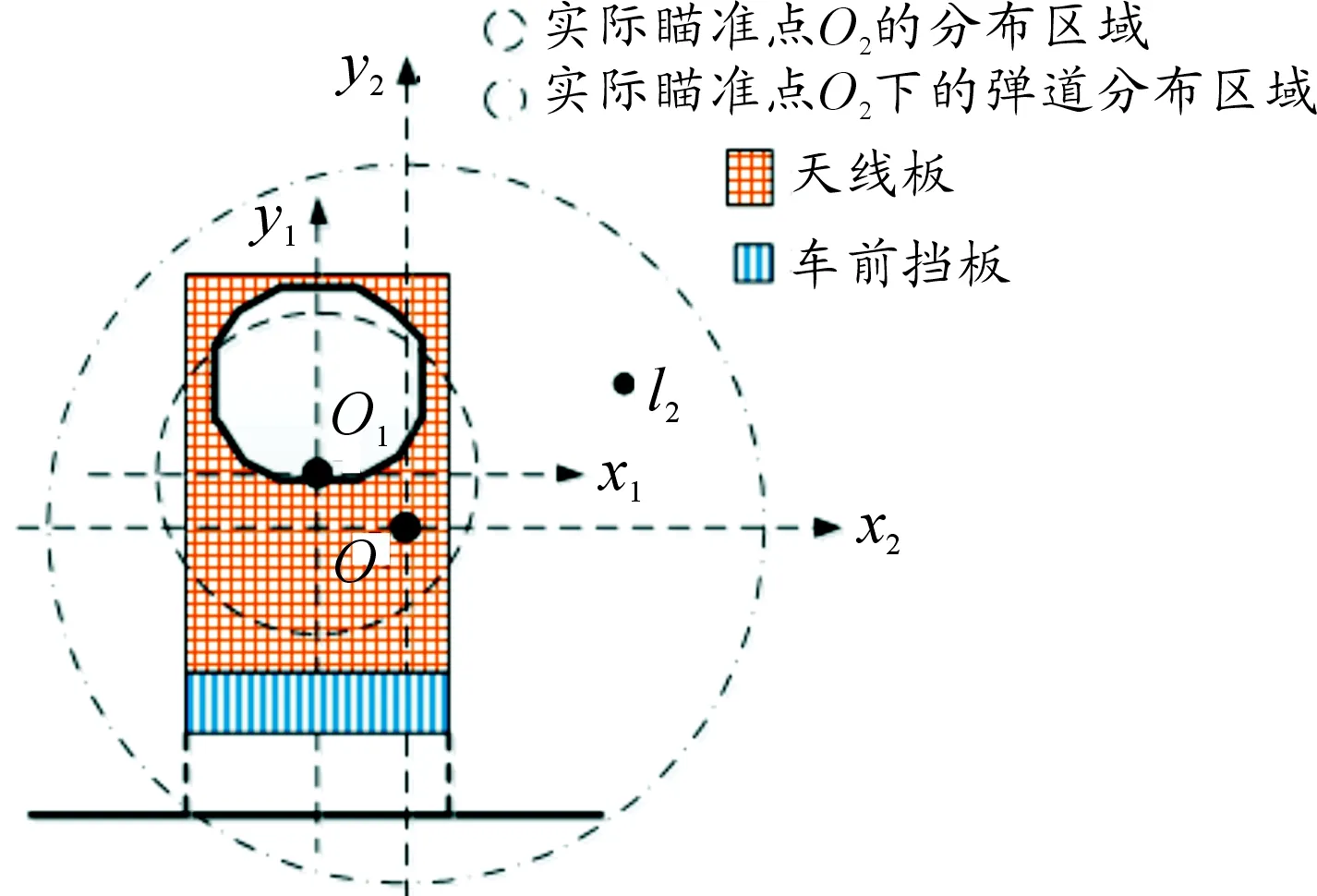
图1 随机弹道l2在弹道平面上的分布

在考虑瞄准点偏差的情况下，对于任意一条随机的实际弹道l2，其导弹对天线板的杀伤概率密度表示为：

f=f1·f2·f3

(1)

式(1)中，f1为任一实际瞄准点O2出现的概率密度。

f1表达式为：

(2)

式(2)中，O2(x1,y1)为任一实际瞄准点在O1x1y1坐标系中的坐标；σ1为以理想瞄准点O1为散布中心的实际瞄准点O2的散布精度，与系统误差的大小相关，σ1=K×N/2；K为瞄准点偏差系数。

f2为在实际瞄准点O2(x1,y1)确定的情况下，任一弹道l2出现的概率密度，表达式为：

(3)

式(3)中，l2(x2,y2)为弹道l2与弹道平面的交点在O2x2y2坐标系中的坐标；σ2为以实际瞄准点O2为散布中心的弹道l2的散布精度，σ2=CEP/1.177 4。

f3为沿弹道l2攻击目标的情况下导弹对天线板的杀伤概率密度。

由式(1)可得单发导弹对天线板的杀伤概率为：

(4)

式(4)中，U={-∞,+∞}；P(x1,y1)为瞄准点为O2(x1,y1)时单发导弹对天线板的杀伤概率，表达式为：

(5)

式(5)中，积分区域D为导弹弹道进入该区域时，f3=1，否则f3=0。

为方便计算，令单发导弹对天线板的无效杀伤概率为P0，即：

(6)

式(6)中，P0(x1,y1)为瞄准点为O2(x1,y1)时单发导弹对天线板无效杀伤的概率，表达式为：

(7)

式(7)中，积分区域E=CUD，导弹弹道进入该区域时，f3=0，即无论采取哪种起爆方式，进入该区域的导弹不能直接命中天线板，或动态破片中心不能击中天线板。因此，只要求积分区域E，即可求得P0(x1,y1)和P。

2 无效杀伤区域的求解

导弹直接命中目标时，在弹道平面上，弹道点分布在雷达天线板在弹道平面投影区域内；导弹近炸毁伤目标时，弹道点分布在目标区域周围，但导弹破片飞散中心形成的圆锥面在弹道平面的投影与雷达天线板在弹道平面的投影有交点。通过在弹道平面内分析弹道点、动态破片飞散中心形成的圆锥半径与天线板投影区域之间的几何关系，可以很方便地求解出有效、无效杀伤区域[13]。

目标在弹道平面上的投影见图2，为方便处理，在O2x2y2坐标系中进行讨论，即图3中的O2xy。设天线板几何中心O1在O2xy坐标系中坐标为(m,n)，弹道点l2坐标为(x,y)，天线板投影后尺寸为M×N，满足：

M=M1sin(α+ζ),N=N1

(8)

式(8)中，α为天线板倾斜角；ζ为弹道倾角。

无效杀伤区域E可归纳为Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域，见图2。

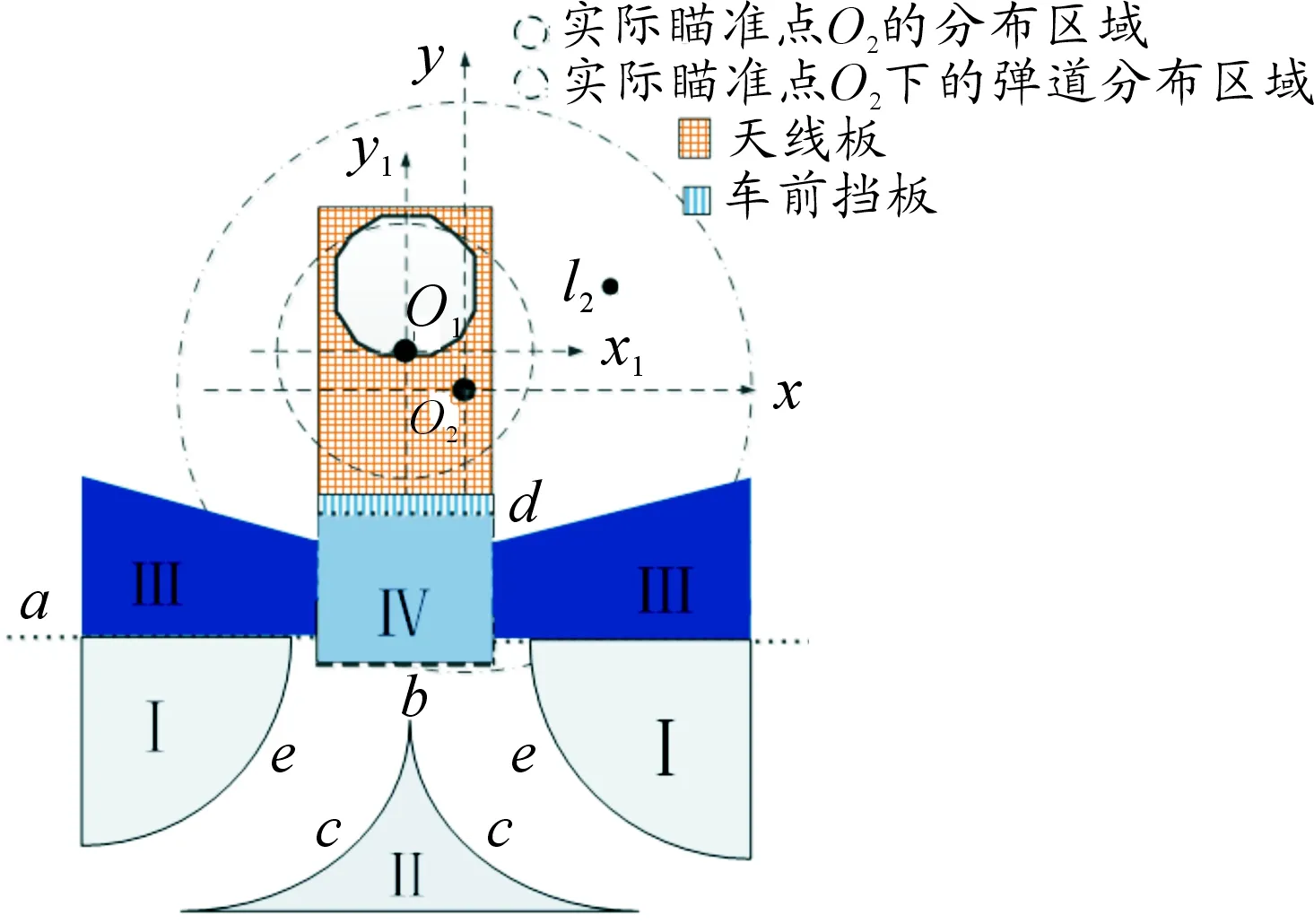
图2 无效杀伤区域在弹道平面上的分布

其中区域Ⅰ为破片中心圆锥面与天线板在弹道平面上的投影不相交，破片不能击中天线板的区域，e线对应破片飞散中心圆锥面与天线板在弹道平面上的投影恰好相交的情况。

区域Ⅱ为天线板在破片中心圆锥面的空腔内，导弹不能击中天线板的区域，c线为天线板恰在破片中心圆锥面空腔内的导弹落点边界线。

区域Ⅲ为导弹在车体侧前方起爆，破片中心圆锥面在天线板下方和探测盲区内，破片不能击中天线板的区域，a线为破片中心恰好击中雷达天线板下边缘的导弹落点边界线。

区域Ⅳ为导弹在车体正前方起爆，破片中心圆锥面被车前挡板挡住或者导弹落在车前挡板上，破片不能击中天线板的区域，b线为破片中心恰好经过挡板边缘命中天线板的导弹落点边界线，线为导弹落在车前挡板上起爆时破片飞散中心恰好击中天线板上边缘的分界线。

求解出图2中的几条分界线，即可求解出无效杀伤区域。

首先求解O1xy坐标系内弹道点坐标为y时动态破片飞散中心形成的圆锥半径R，如图3所示。

图3 动态破片飞散中心形成的圆锥半径

解得：

(9)

式(9)中，β为破片动态飞散角；L0为导弹战斗部中心至导弹前端的距离；H2为车前挡板的离地高度。

2.1 分界线a

分界线a在弹道平面的意义如图4所示。

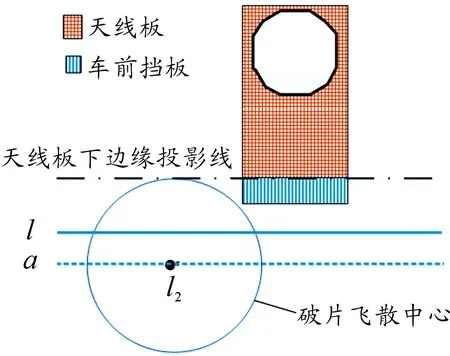
图4 弹道平面内的边界线a

满足：

R=ya-M/2

(10)

式(10)中，ya为弹道平面内直线a距离理想瞄准点O1的距离。解得：

(11)

式(11)中，

2.2 分界线b

分界线b在侧视图上的几何关系如图5所示。

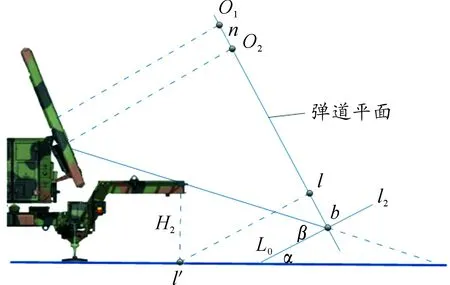
图5 边界线b在侧视图上的几何关系

根据图5所示几何关系，可求得b线距离理想瞄准点O1的距离yb为：

(12)

2.3 边界线c

天线板在破片飞散中心圆锥面空腔内的边界情况如图6所示。图6中当弹道l2经过D点时，破片飞散中心圆锥面与天线板的相交情况。圆弧c为随x变化临界点D形成的轨迹。

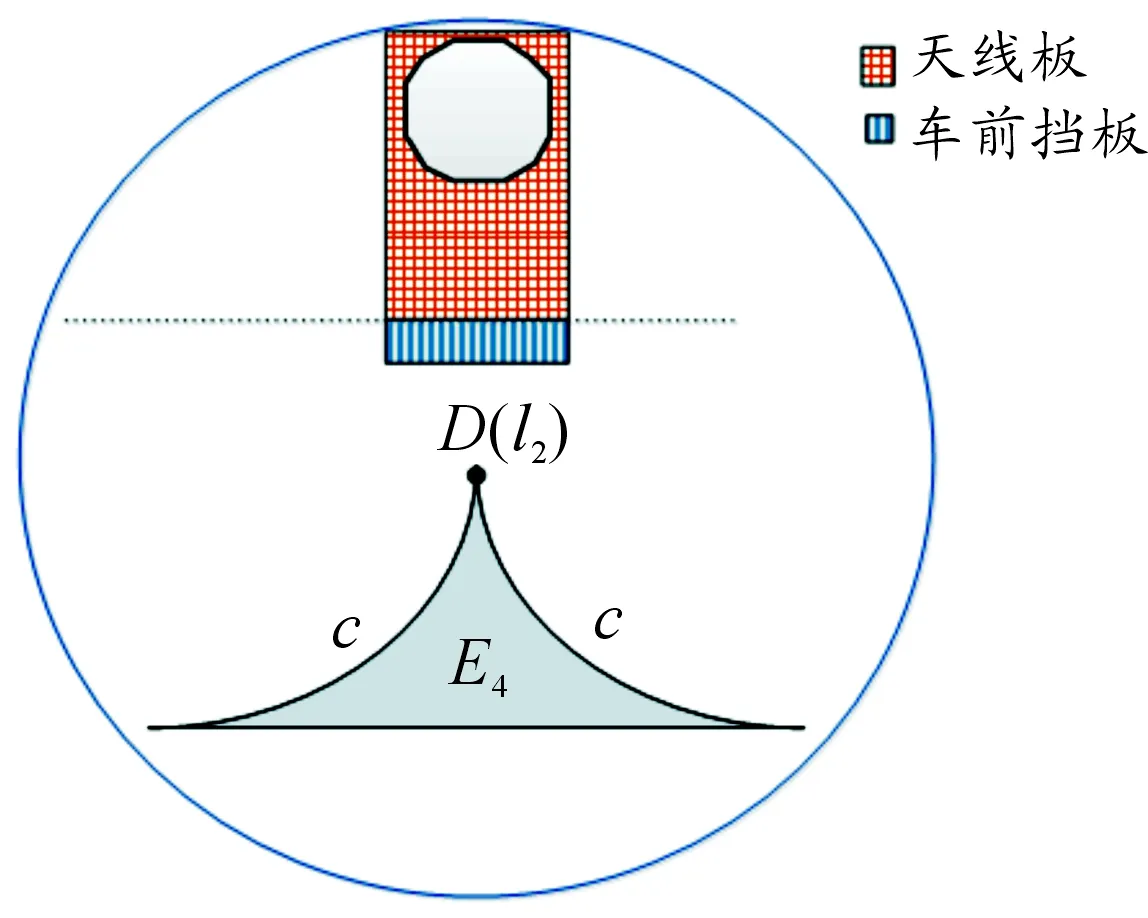
图6 破片飞散中心圆锥面空腔与天线板关系

(13)

式(13)中，

2.4 边界线d

导弹命中车前挡板边缘，若此时破片飞散中心能够击中天线板，则所有命中挡板的情况均能对天线板造成有效杀伤；若此情况下不能击中天线板，则需讨论击中天线板的边界情况，即讨论弹道面内直线d的分布。图7为侧向示意图，图7中d点对应图2中的d线。

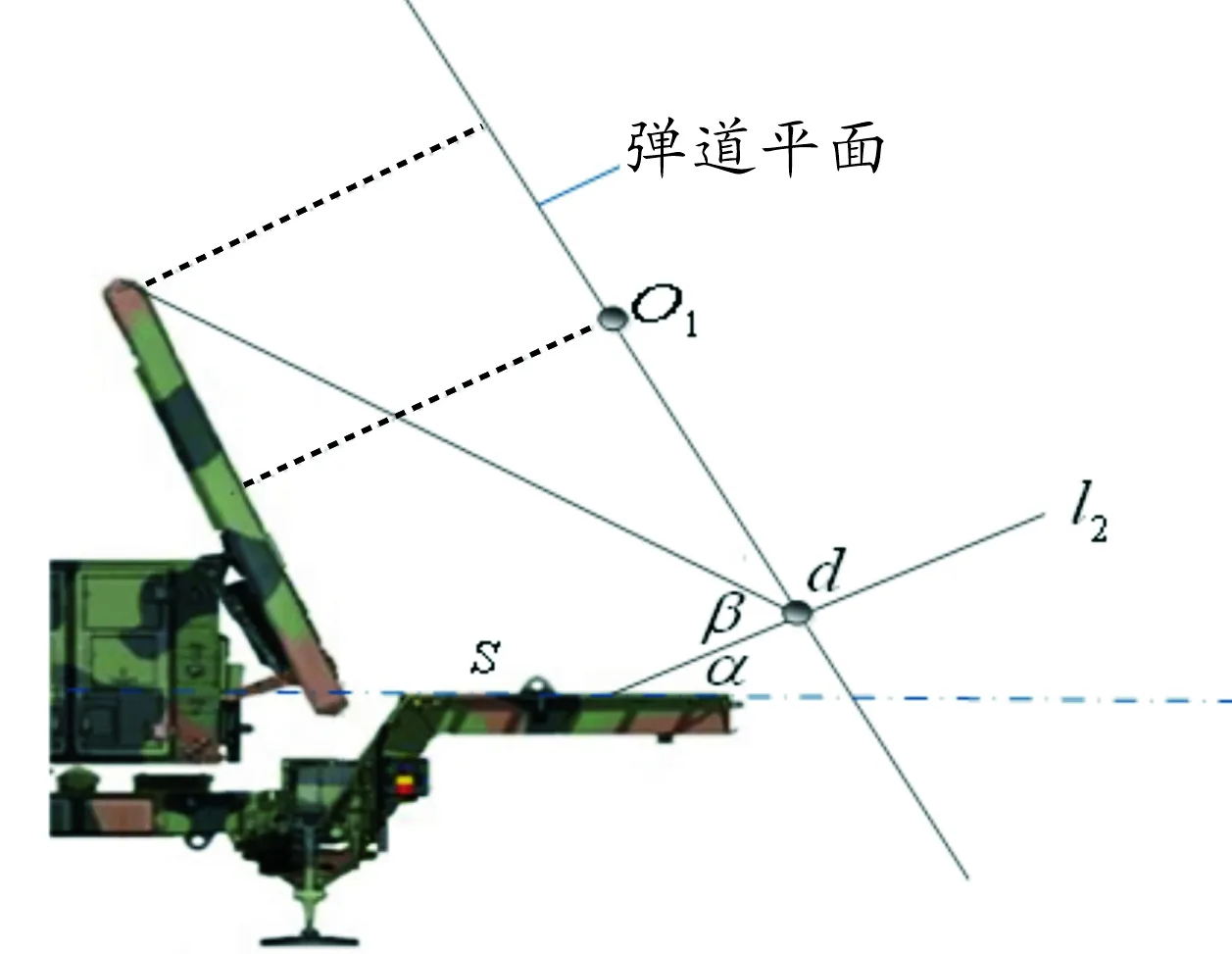
图7 导弹命中车前挡板侧向示意图

此时，d线距离理想瞄准点O1的距离yd为：

(14)

式(14)中，

2.5 边界线e

边界线e对应破片飞散中心圆锥面与天线板在弹道平面上的投影恰好相交的情况，如图8所示。当弹道坐标点纵坐标为y时，设有效毁伤区域的两个边界弹道l2、l2′的横坐标分别为x1和x2，弹道l2、l2′随y的变化所形成的轨迹为区域Ⅰ的弧形边界线。

图8 边界弹道l2、l2′的破片飞散中心圆锥面与天线板关系

(15)

2.6 无效杀伤区域

通过上述分析可得无效杀伤区域E：

E1区域为：

(x,y)∈{x≤x1∪x≥x2，y≤ya}

E2区域为：

(x,y)∈{x3≤x≤x4，y≤n-yc}

E3区域由两部分组成，分别为：

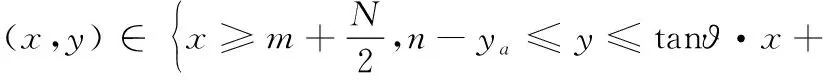
E4区域为：

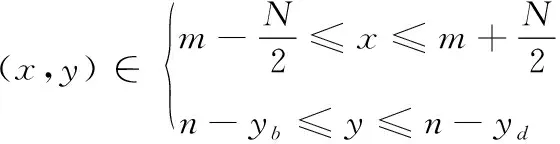
无效杀伤区域E确定后，用(x,y)替换(x2,y2)，依据式(7)可确定无效杀伤概率P0(x1,y1)，依据式(6)可确定单发毁伤概率P。

3 仿真计算

假设ARM攻击PAC-3的制导雷达，雷达车天线板倾角为67.5°，车前挡板长2.87 m，距离地面高度2.06 m，导弹CEP为5 m，导弹末段弹道近似认为直线，破片式战斗部破片初速度1 550 m/s，静态飞散角为68°。根据第1节制导雷达参数，利用Matlab软件对弹速为2Ma和弹道倾角为15°的情况进行仿真计算，限于篇幅，仅列出部分情况仿真结果以说明模型的有效性，结果见图9、图10。

图9 弹速为2Ma时单发毁伤概率随弹道倾角变化曲线

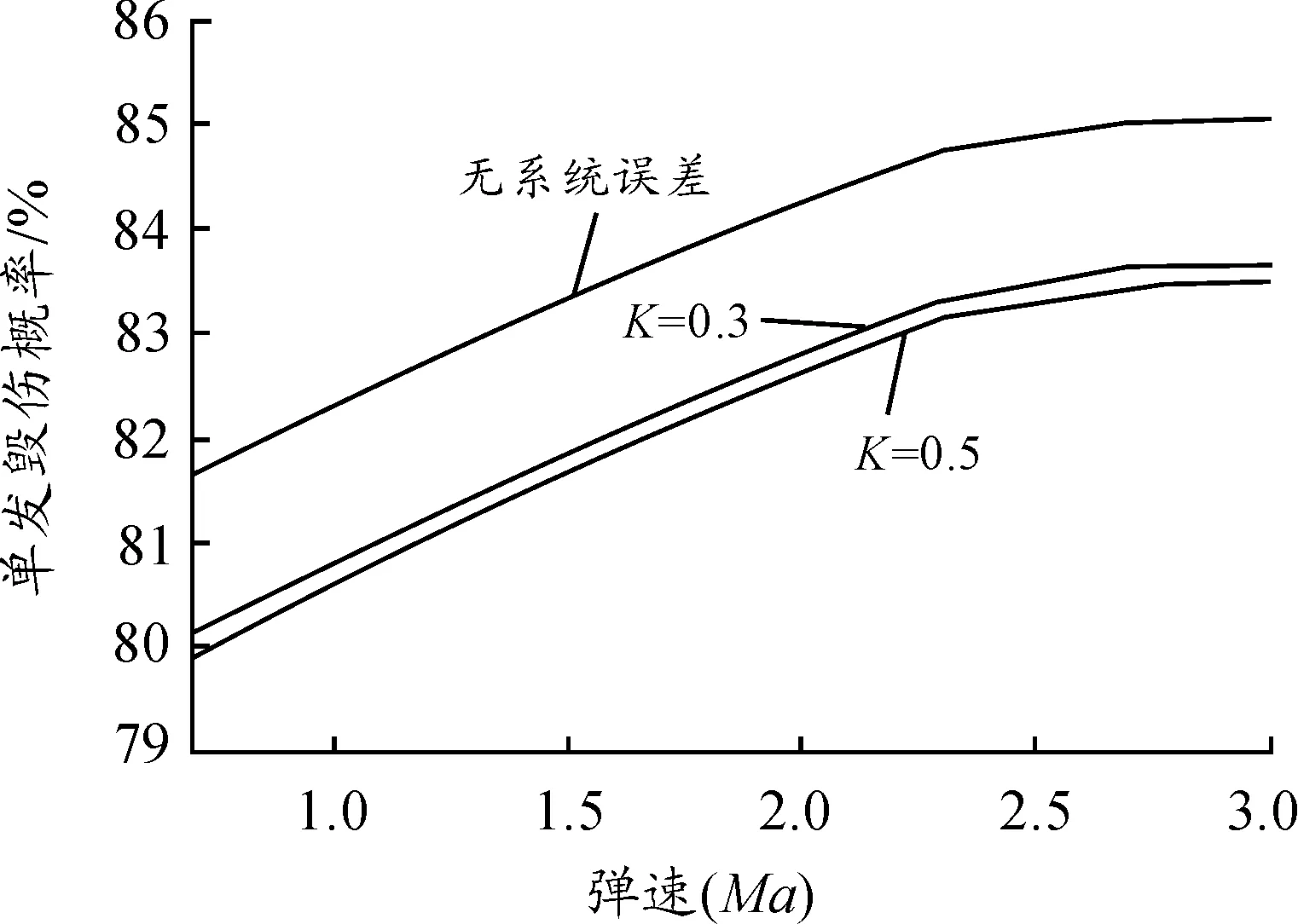
图10 弹道倾角为15°时单发毁伤概率(%)随弹速(Ma)变化曲线

从图9可以看出，弹道倾角越大，单发毁伤概率越大，这主要是因为小入射角攻击时，战斗部发射的破片群不能有效充分地对向目标；从图10可以看出，弹速越高，单发毁伤概率越高，这是因为弹速越高，破片的动态飞散角越小，目标前方的有效杀伤区域越大，这些特性论证了模型的有效性。

系统误差会降低破片式ARM的单发毁伤概率，偏差系数越大(即系统误差越大)，破片式ARM单发毁伤概率越小。

4 结论

本文针对系统误差对破片式ARM单发毁伤概率的影响问题，通过建立破片式ARM单发毁伤概率计算模型，计算导弹无效杀伤区域，量化分析了系统误差对破片式ARM单发毁伤概率的影响程度。通过仿真，验证了模型的有效性。本文的工作为量化研究破片式ARM的作战效能奠定了一定的基础，同时可为破片式ARM的作战使用提供相关理论依据。