结构参数对小长径比装药形成EFP的影响
赵飞扬,王志军,王雪飞
(中北大学 机电工程学院, 太原 030051)
主战坦克的防护能力正在与日俱增,车体和炮塔都是使用了特殊的材料制作而成的坚固壳体。目前的主战坦克车体和炮塔的前装甲最厚并且倾角较大,对于有些坦克的前装甲,弹药所需穿透的装甲厚度甚至达到了800 mm以上,可以有效地防御正面的火力威胁。目前各国的主战坦克基本都会在车体前方、侧面以及炮塔上披挂反应装甲,这进一步增加了破甲的难度。相对而言,车体顶部、后部、侧面及底部的装甲比较薄,而且坦克顶甲和底甲也较难装备反应装甲。针对坦克的这种结构,对坦克薄弱部分进行打击的武器应运而生,末敏弹就是这样一种武器[1]。在现代战争中,由于战场目标的多样化,根据目标特性,针对不同目标使用不同毁伤效果的战斗部可得到事半功倍的效果。
随着爆炸成型弹丸(EFP)战斗部侵彻能力与作用距离的不断提高,并且对于大长径比装药形成的EFP有了较为完善的研究[2-6],末敏弹这种灵巧弹药的研发水平已经成为了衡量各国反装甲作战能力的标准之一。EFP战斗部是末敏弹的重要组成部分,其作用距离和侵彻能力决定了末敏弹系统作战效能的优劣,近年来国内学者对末敏弹的研究取得了很多成果[7-11]。在末敏弹子弹药中,EFP战斗部是占据弹内空间最多的部分,故进一步提高EFP战斗部的紧凑程度和威力以及减小装药长径比已经成为了末敏弹系统相关技术中的一个研究重点。
通常而言,小长径比战斗部是指长径比小于0.8的战斗部结构。本文采用LS-DYNA软件对100 mm口径的小长径比EFP战斗部进行了数值模拟,研究了长径比、药型罩结构参数、药型罩的形状对于EFP成型的影响。
1 小长径比战斗部的计算模型
几何模型采用如图1所示的战斗部结构,其中计算装药为8701炸药,装药直径CD=100 mm,装药高度为80 mm。药型罩采用球缺形药型罩,材料为紫铜,药型罩直径为D=90 mm,并附有挡环。起爆方式为装药顶端中心点起爆。

图1 战斗部结构几何模型
本文运用Truegrid前处理软件进行网格划分,建立如图2所示的小装药长径比爆炸成型弹丸的有限元模型。由于该结构为轴对称结构,所以有限元模型采用1/4结构划分网格并添加对称约束的方式来以减少模型单元数目,节约计算时间。为简化计算,本文模型中不考虑壳体影响,仅考虑药型罩、炸药和挡环。选用Lagrange算法来模拟EFP的形成过程,网格单元选用solid164八节点六面体单元。药型罩和挡环采用*MAT_JOHNSON_COOK材料模型和GRUNEISEN状态方程,炸药采用*MAT_HIGH_ EXPLOSIVE_BURN材料模型、JWL状态方程。药型罩、炸药材料参数值见文献[12]。使用的单位制为:mm-ms-kg-GPa。
2 爆炸成形弹丸成型过程
为研究小长径比战斗部形成EFP的机理,对装药口径为CD=100 mm,战斗部长径比为0.8,曲率半径R=125 mm,药型罩壁厚为δ=4 mm的带挡环的装药结构进行数值模拟,起爆方式为装药顶端中心点起爆。

图2 战斗部有限元模型
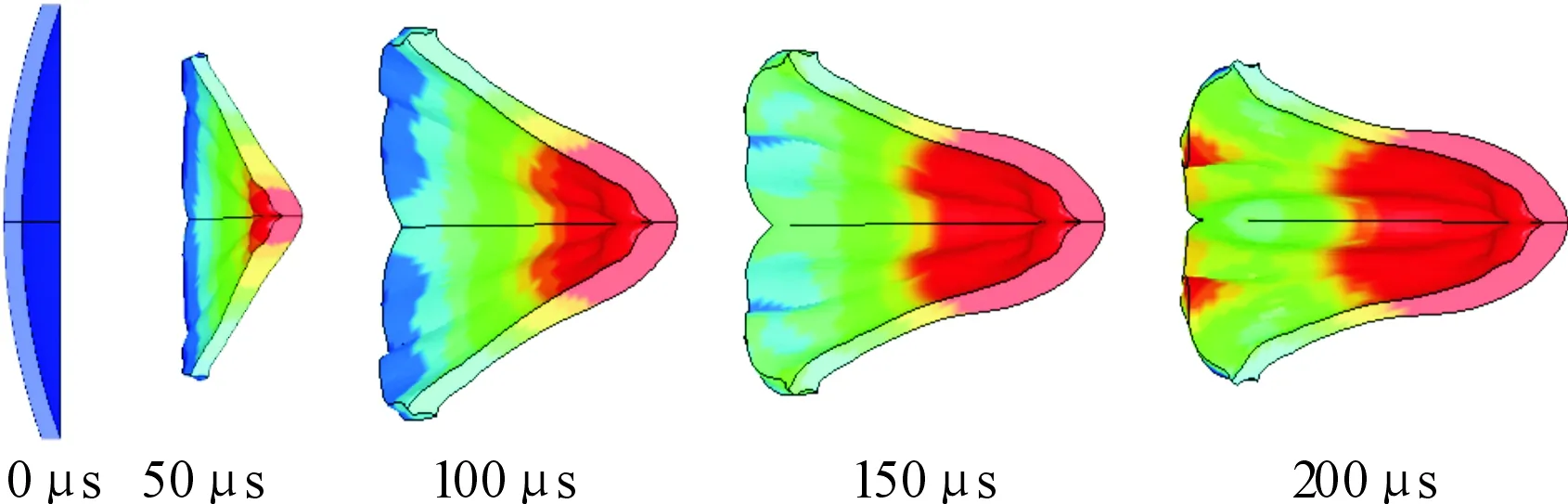
如图3所示,主装药起爆后大约8 μs,药型罩受到炸药爆轰压力和爆轰产物的冲击和推动作用,开始被压垮变形,在22 μs时,罩顶微元首先被压垮变形,药型罩了发生翻转,罩壁微元向对称中心集中,在对称中心发生堆积并且发生相互挤压、碰撞,药型罩被压合形成弹丸的形状向前高速运动。由于有速度梯度,EFP会在运动中被逐渐拉长。最终在t=200 μs时,侵彻体头尾速度趋于一致,速度差小于20 m/s,形成稳定的EFP。

图3 不同时刻形成侵彻体的外形
3 小长径比战斗部数值模拟结果分析
3.1 战斗部的药型罩形状对EFP成型的影响
为了研究小长径比战斗部的药型罩形状对EFP成型的影响,对锥角为150°的圆锥形药型罩与曲率半径R=125 mm的球缺形药形罩所形成EFP的形状进行了对比。药型罩均为等壁厚药型罩,厚度δ为4 mm。装药直径CD=100 mm,装药高度为80 mm,战斗部长径比为0.8。数值仿真计算结果如图4所示。
由计算结果可知:圆锥形药型罩的头部速度为1 754 m/s,球缺形药型罩的头部速度为1 363 m/s。速度相差391 m/s。圆锥形药型罩相比于球缺形药型罩,形成的EFP长度长,直径小,而球缺形药型罩所形成的EFP头尾速度差小,直径大,尾部由于药形罩向后翻转形成了四片尾翼状褶皱,具有优秀的空气动力学外形,可以使EFP长距离飞行而不失稳。
两种药形罩结构各有优势,鉴于球缺罩的成型较为容易观察。
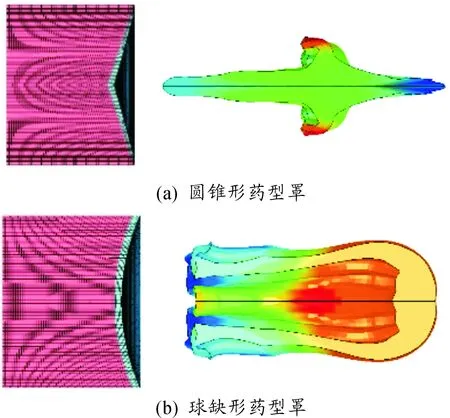
图4 200 μs时不同药型罩形成侵彻体的外形
3.2 曲率半径R对EFP成型的影响
在分析药型罩圆弧段曲率半径对EFP成型影响时,分别取R在100 mm,125 mm,150 mm,175 mm,200 mm,225 mm(间隔25 mm)时侵彻体性能的变化。数值模拟计算结果如图5、图6所示,由于篇幅所限,这里只给出了200 μs时EFP的形态。
由计算结果可知:随着曲率半径的增加,侵彻体长度逐渐变短,尾裙逐渐变大。形成各侵彻体的长径比逐渐减小,EFP速度相差在50 m/s以内。曲率半径在R<125 mm时形成具有较高头尾速度差和较大的长径比的EFP,气动性能较为优秀。曲率半径在R=125~225 mm头部逐渐变粗,侵彻体长径比减小。但EFP过小的长径比会使其质心前移,并受到更大的空气阻力,在爆炸成型弹丸难以旋转的条件下极易失稳,甚至在空气中发生翻转,进而失去对靶板的侵彻能力。
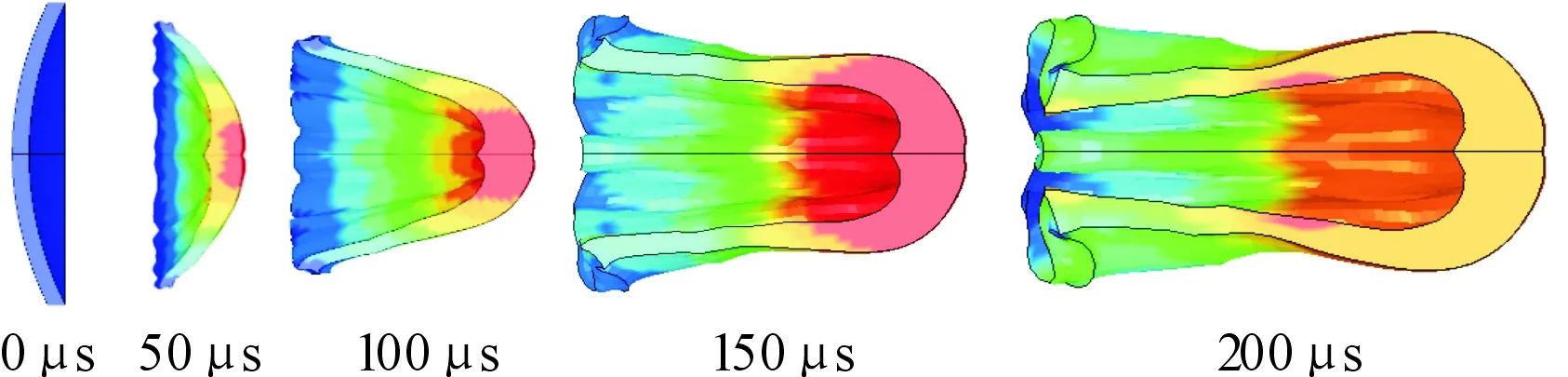
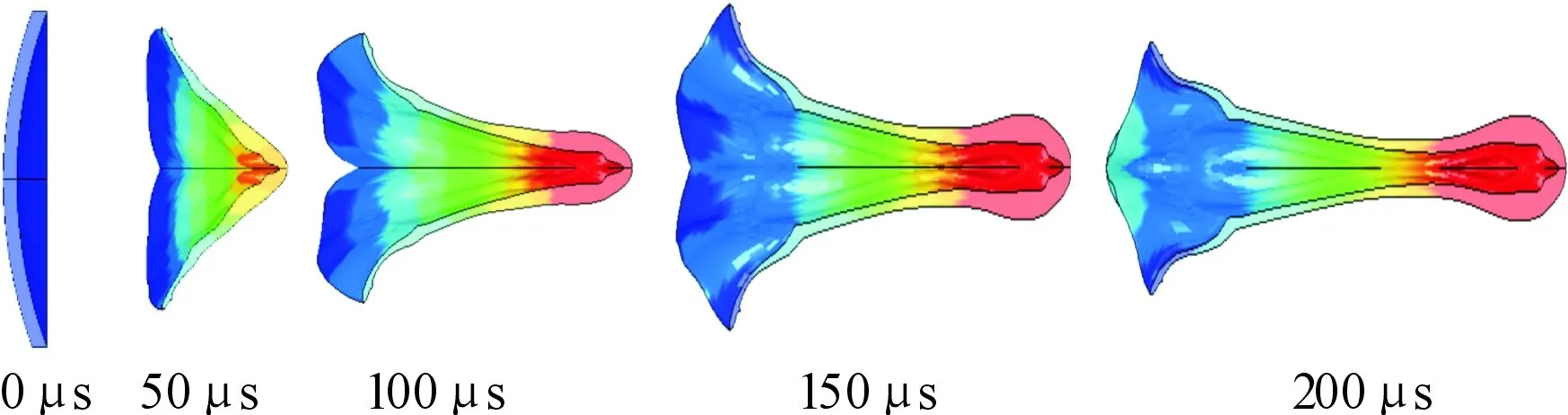
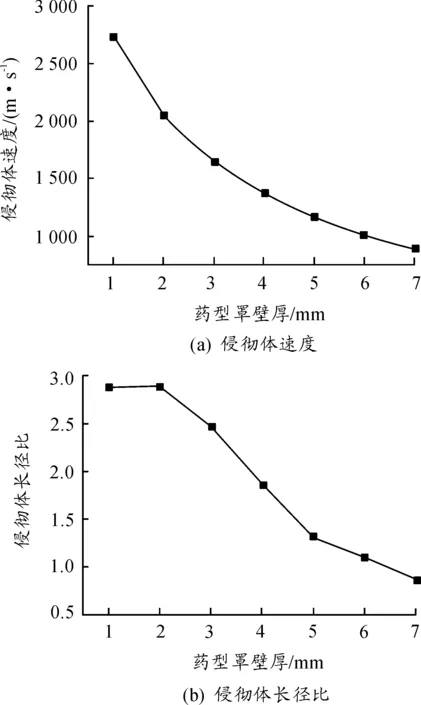
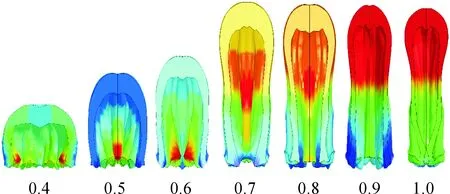
由图6可以看出:由于球缺形药型罩所形成的EFP长径比在125~175 mm这一阶段减小明显,大于175 mm,长径比小于1.2时的部分趋于稳定,EFP侵彻能力降低。故本文中拟认为曲率半径125 mm 图5 200μs时不同曲率半径R形成侵彻体的外形 图6 侵彻体参数随曲率半径的变化 为了分析起爆方式对于小长径比EFP成型的影响,分别讨论了药柱装药顶端中心点起爆、药柱顶端环形起爆、药柱底端逆序起爆3种起爆方式。取药型罩壁厚为4 mm,曲率半径R为125 mm。数值仿真结果如图7~图9所示。 图7 中心起爆时EFP的成型过程 图8 环形起爆时EFP的成型过程 图9 逆序起爆时EFP的成型过程 由计算结果可知:当使用逆序起爆时,形成的EFP长径比为1.27,但是速度偏低,头部只有1 000 m/s;当使用环状起爆时,形成的EFP速度高,头部可以达到1 896 m/s。EFP尾翼形状好,气动性能良好[13]。但是EFP被长径比为3.89,向杆式射流发展,头部出现颈缩,有可能会断裂,不利于EFP在空中进行长距离的飞行;中心起爆方式产生的EFP速度是1 363 m/s,介于逆序起爆与中心起爆之间。外形好,长径比为3.40,能产生气动外形良好的尾裙结构。 为分析药型罩厚度δ对EFP成型的影响。选取药型罩圆弧段曲率半径R=125 mm,壁厚δ分别取1 mm、2 mm、3 mm、4 mm、5 mm、6 mm、7 mm(间隔1 mm)。计算结果如图10、图11所示。 图10 200 μs时不同药型罩壁厚H成型效果图 图11 侵彻体参数随药型罩壁厚的变化 由计算结果可知:随着药型罩厚度的增加,形成侵彻体的头部质量逐渐增加,尾裙变大。形成侵彻体的头部速度、头尾速度差、长度和长径比都减小。药型罩壁厚较小时,罩材在受到爆轰波冲击变形后,速度梯度过大,EFP被拉得非常长,必然会引发断裂和失稳,不能形成稳定的EFP。随着壁厚的增加,EFP速度逐渐降低,长度变短。由于弹丸的动能与EFP速度的二次方成正比,与整体质量的一次方成正比,即速度对EFP的整体动能影响比质量的影响要大。所以弹丸的动能会随着壁厚的增加而减小,侵彻能力相对减弱。因此在一定的范围内,可以通过减小药型罩壁厚来提高其侵彻性能。厚度δ<4 mm 时,形成的EFP出现了径缩,进而可能会引发断裂。4 mm<δ< 6 mm时,能够形成稳定的EFP。 为进一步分析长径比对于EFP成型的影响,选取药型罩壁厚δ=4 mm,曲率半径R为125 mm,起爆方式为顶端中心起爆。在口径不变的情况下分别取药柱高度为40 mm、50 mm、60 mm、70 mm、80 mm、90 mm、100 mm,所以战斗部长径比分别为0.4、0.5、0.6、0.7、0.8、0.9、1.0。(间隔0.1)。数值仿真结果如图12、图13所示。 图12 200 μs时不同长径比成型效果图 图13 侵彻体参数随装药长径比的变化 由仿真结果可以发现,随着长径比的增加,EFP头部质量减小,速度会变高,尾裙变小。对于小长径比弹丸来说,减小长径比使装药减少,结构紧凑。普遍认为,战斗部长径比小于0.8的聚能装药为小长径比聚能装药,因此设置0.9与1.0两个非小长径比的对比组。由仿真结果可以看出,较小的长径比同样可以形成较大直径的EFP。但是由仿真结果可以看出来,装药长径比越小,EFP的长径比就越小,尾裙形状变差,这将会导致EFP在飞行中具有较差的飞行稳定性,容易在飞行过程中偏离弹道,甚至断裂和翻滚。 1) 药型罩圆弧部曲率半径125 mm 2) 起爆方式对于小长径比结构形成的EFP影响大,环形起爆速度高,逆序起爆成型好。在将来的研究中可以考虑使用环形起爆与逆序起爆来提高小长径比结构的形成EFP的性能; 3) 球缺罩形成的EFP直径大,速度差小,可以达到更深的穿孔和更大的孔径。本文研究的是等壁厚球缺形药型罩,在将来的研究中可以尝试变壁厚药型罩,可以防止前后速度差过大而断裂。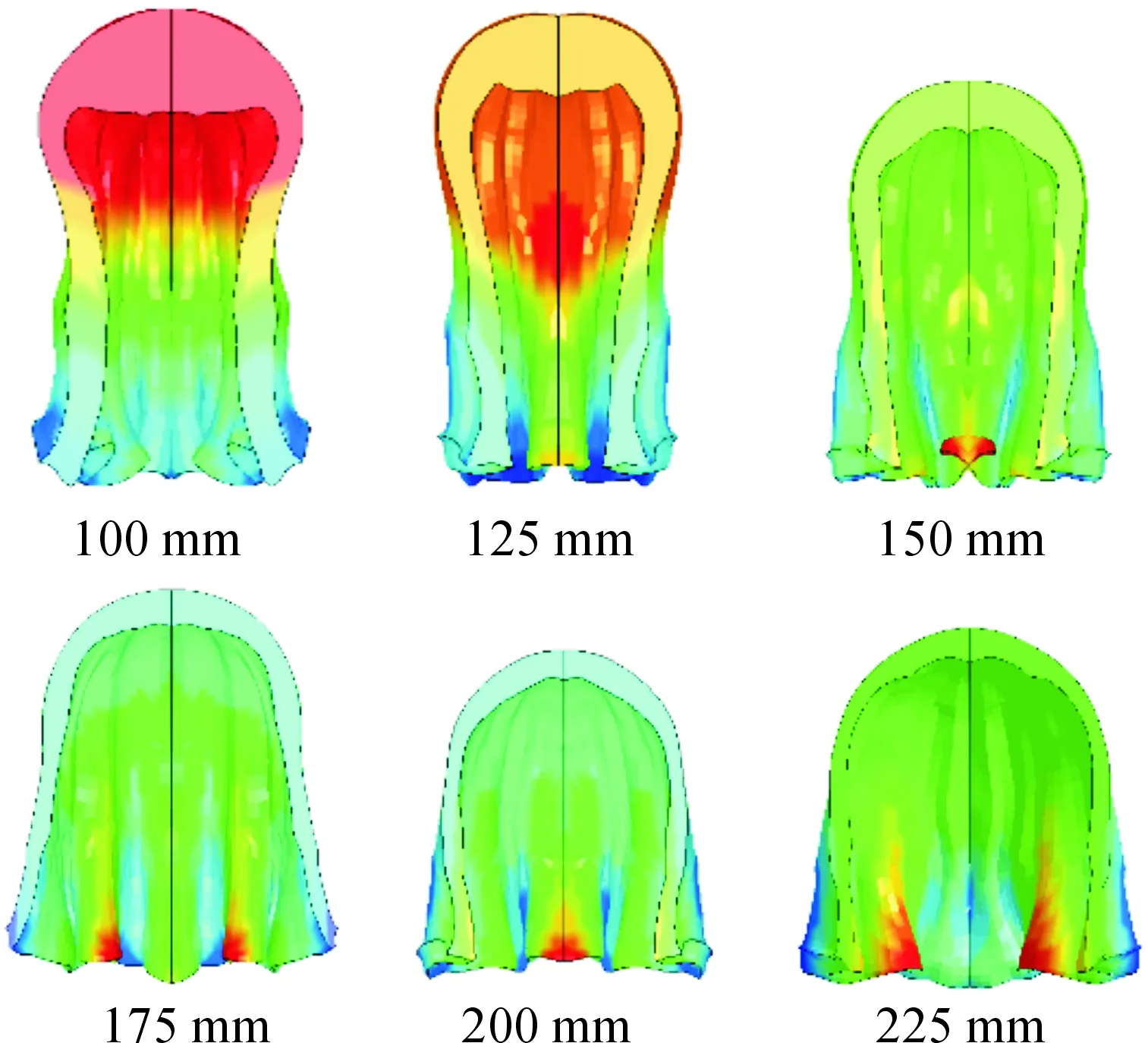

3.3 起爆方式对EFP成型的影响
3.4 药型罩厚度δ对EFP成型的影响

3.5 长径比对EFP成型的影响

4 结论

