多锥结构药型罩侵彻性能数值模拟研究
姜彦东
(大庆油田射孔器材有限公司, 黑龙江 大庆 163853)
随着装甲目标和应用领域的拓展,传统的单锥药型罩结构已不能满足需要,双锥以及多锥药型罩能够形成性能更好的射流毁伤元,许多学者对多种药型罩结构展开了大量研究[1-4]。
多锥结构药型罩在单锥药型罩的基础之上减小了罩顶锥角,加大罩底锥角,其形成的射流头部速度得到了提高。Walters等[5]建立了双锥形药型罩射流的侵彻计算模型,提出了所形成射流具有双线性速度分布特性;郭帅等[6]通过数值模拟方法研究了双锥形药型罩过渡点位置对射流形成的影响;杨晓红等[7]通过试验获得了不同双锥形药型罩在不同炸高下的静破甲深度,并利用理论分析和数值模拟方法得到了双锥药型罩的最佳炸高;赵海平等[8]设计了一种锥-锥结合药型罩,改变上、下锥罩的高度比例和下锥罩锥角,分析组合药型罩形成射流的规律;刘宏杰等[9]基于环形切割聚能装药战斗部及灰关联理论,通过数值模拟方法对环形双锥罩聚能装药结构进行了优化设计;陈闯[10-13]利用冲击波Hugoniot关系修正伯努利方程,结合改进的PER理论建立了考虑冲击波、射流速度分布及射流状态等影响因素的侵深计算模型。刘润滋等[13]对不同罩高的变壁厚和等壁厚双锥药型罩进行了数值模拟研究,得到了上下罩高比例与射流速度的关系;王子明等[14]在双锥药型罩基础上进行优化,提出一种辅助型双锥药型罩,优化后通过数值模拟证明射流头部最大速度与射流长度得到了有效提升,同时降低头部速度下降梯度,达到了提升射流侵彻性能的目的。
1 理论模型
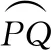
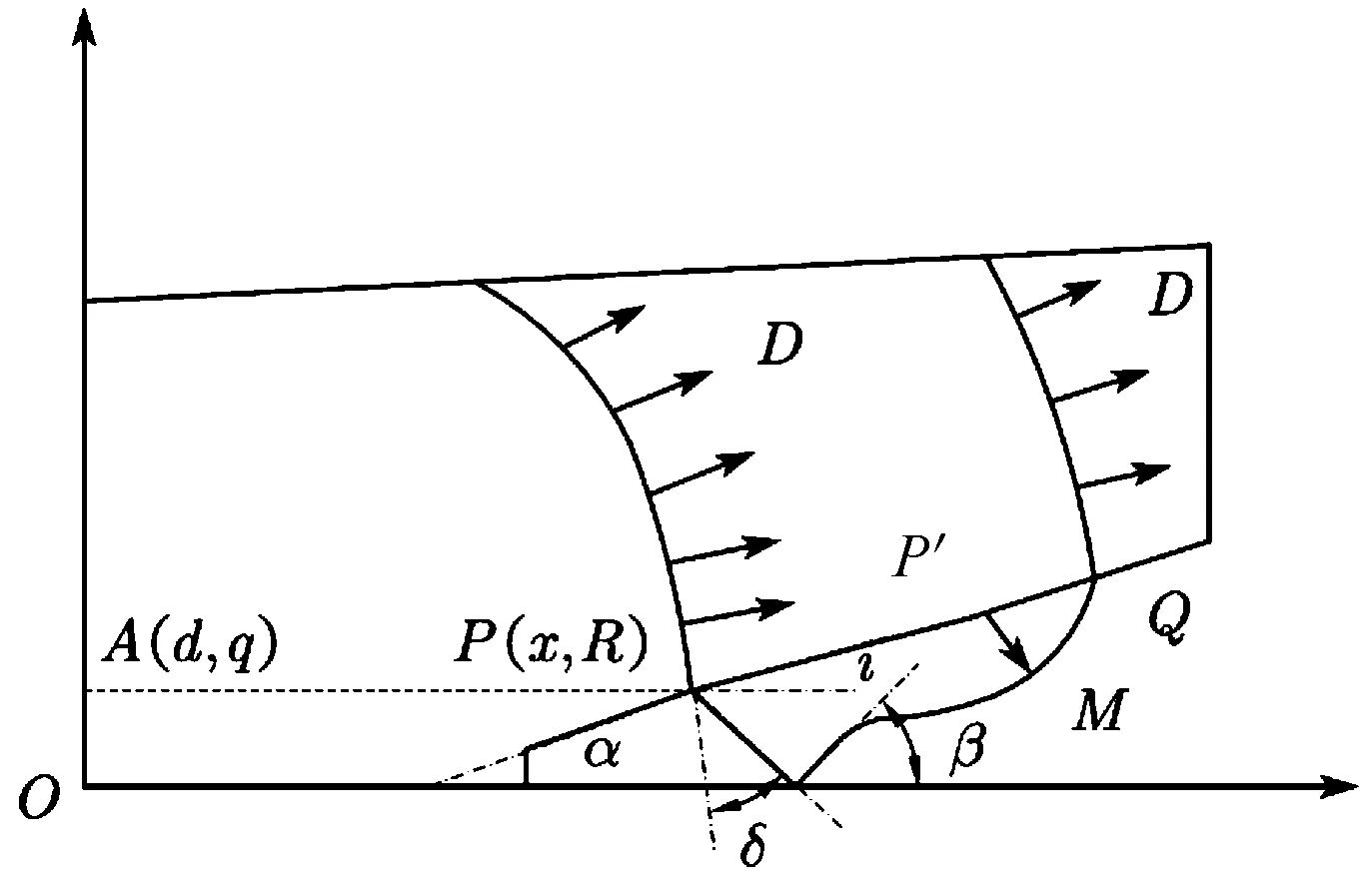
图1 变锥角药型罩压垮模型示意图
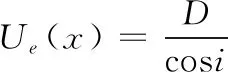
(1)
式(1)中,i=i(x)为爆轰波波阵面与罩表面相交处波阵面的法线与该点罩表面的切线的夹角。在药型罩的压垮过程中,爆轰波与药型罩的相互作用被认为是稳态过程。
假设O点加速度为常数,则药型罩在任意时刻的压垮速度为
Vc(x,t)=a(t-t0)t≤tm
(2)
Vc(x,t)=V0t>tm
(3)
式中,a为加速度;t0为爆轰波波阵面从起爆点到药型罩P′点处的时间;V0为药型罩的压垮速度;tm为药型罩停止加速时间。若P点的坐标为(x,R),起爆点A的坐标为(d,q),则
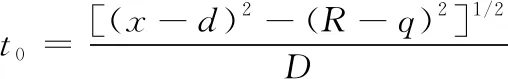
(4)
根据泰勒关系式,抛射角为

(5)
则
(6)
为了求得压垮角β,现取药型罩表面任一点P′,在时间t内,罩微元从P′点压垮到M,设M点坐标为(z,r),则

(7)
式中,α为P′点处罩表面切线与z坐标轴的夹角,l(x,t)为罩微元从P′到M点的距离。
l(x,t)=V0(t-t0)
(8)
一般来说,有意义的压垮角是指罩微元到达轴线上的压垮角,所以,由式(7)和式(8)可知,在r=0时,罩微元运行的时间为
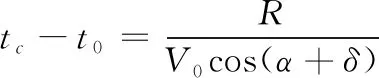
(9)
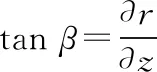
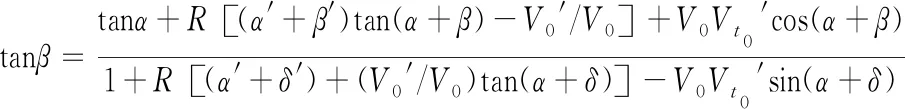
(10)
式中,变量的“′”代表坐标位置的微分,其中
(11)
根据图中几何关系知
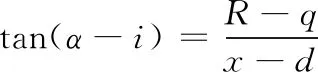
(12)
则
(13)
根据定常不可压缩流体力学理论,可以得到射流和杵体速度为
(14)
(15)
再根据碰撞点处质量守恒和动量守恒关系得到
(16)
(17)
式中,dm为罩微元质量;dmj为碰撞后形成射流的质量;dms为碰撞后形成杵体的质量。据此可以计算出射流的速度和质量,进而计算出其具有的动能。
2 数值模拟模型建立
2.1 聚能装药结构模型
药型罩直径为45 mm,单锥药型罩锥角为40°,装药高度60 mm,药型罩厚度2 mm,壳体厚度为2.5 mm,炸高为50 mm,靶板厚度为300 mm。
装药和药型罩具有对称结构和对称载荷,为了提高计算效率,建立1/4模型,施加对称约束。数值模拟模型由炸药、药型罩、空气域、壳体以及靶板五部分组成。其中炸药、药型罩、空气域基于Euler网格建模,壳体及靶板采用Lagrange网格建模,并且两种网格之间采用耦合算法,单元使用多物质ALE算法。采用八节点六面体网格,其中,射流作用区域网格加密[15]。在空气域自由表面设置无反射边界条件,保证冲击波到达边界时不产生反射。起爆方式为中心点起爆。单位为cm-g-μs。计算有限元模型如图2所示。

图2 有限元模型示意图
2.2 材料模型及参数
RDX炸药使用High Explosive Burn材料模型,具体参数见表1。
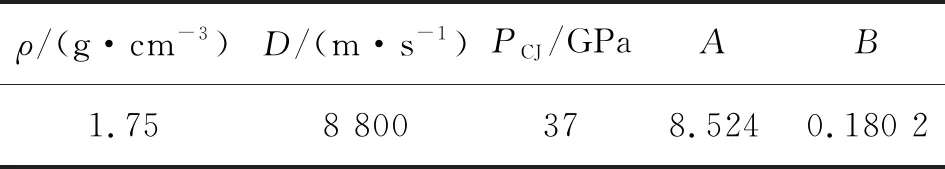
表1 RDX炸药参数
药型罩采用铜钨合金粉末压制,采用Steinberg材料模型和Gruneisen状态方程,具体参数见表2。

表2 铜钨合金参数
空气采用Null材料模型和Linear Polynomial状态方程,具体参数如表3所示。

表3 空气参数
壳体采用Plastic Kinematic材料模型,具体参数如表4所示。

表4 壳体参数
钢靶采用Johnson Cook材料模型,并采用Gruneisen状态方程,主要参数见表5。

表5 钢靶参数
3 数值模拟结果与分析
3.1 锥数对侵彻性能的影响
使用LS-DYNA进行数值模拟,通过改变药型罩锥数,研究锥数对射流侵彻性能的影响规律。分别对单锥、双锥、三锥、四锥、五锥药型罩侵彻钢靶过程进行数值模拟,单锥药型罩锥角为40°,此后每增加一锥,锥角增加4°,变锥位置为基于锥数的等分位置,数值模拟方案如表6所示,药型罩模型如图3所示。

表6 不同锥数药型罩数值模拟方案
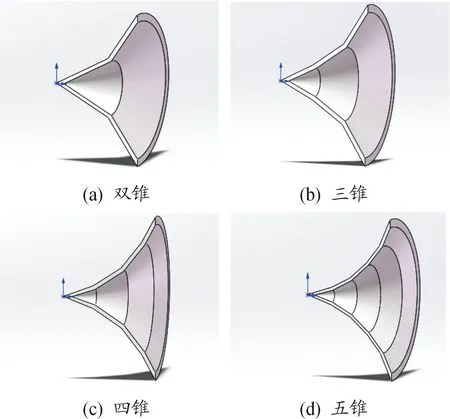
图3 药型罩模型示意图
通过数值模拟得到的不同锥数药型罩侵彻钢靶深度如表7所示,不同锥数药型罩射流头部最大速度如图4所示。

表7 不同锥数药型罩侵彻深度 mm
由表7可以看出,双锥形药型罩对钢靶的侵彻性能最好,具有最高的侵彻深度,为226.2 mm;三锥药型罩其次,比双锥降低2.785%,单锥药型罩和四锥药型罩侵彻深度接近,相对双锥药型罩侵彻深度降低5.968%和5.261%,五锥药型罩的侵彻深度最低,较双锥药型罩降低15.782%。不同锥数药型罩侵彻深度排序为:双锥>三锥>四锥>单锥>五锥。由图4可以看出不同锥数药型罩射流头部速度变化趋势,其速度大小排序与侵彻深度排序相同。速度最大的双锥药型罩射流头部速度为7 986 m/s,三锥、四锥药型罩射流头部速度较为接近,为7 894 m/s和7 883 m/s,同双锥药型罩相比分别降低1.152%和1.289%,单锥药型罩和五锥药型罩射流头部速度较双锥罩分别下降2.554%和5.284%。不同锥数药型罩侵彻过程动能变化曲线如图5所示。
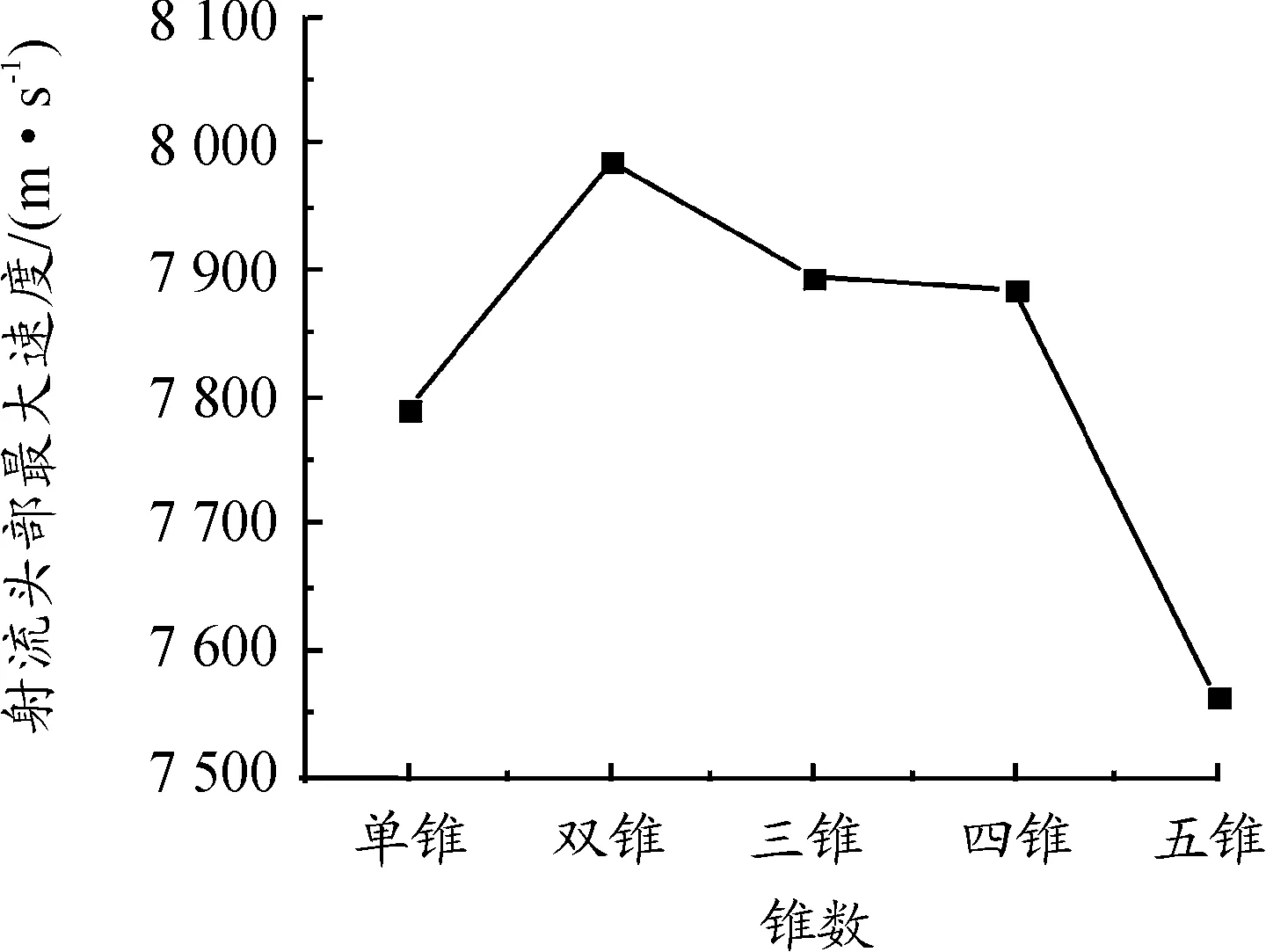
图4 不同锥数药型罩射流头部最大速度曲线
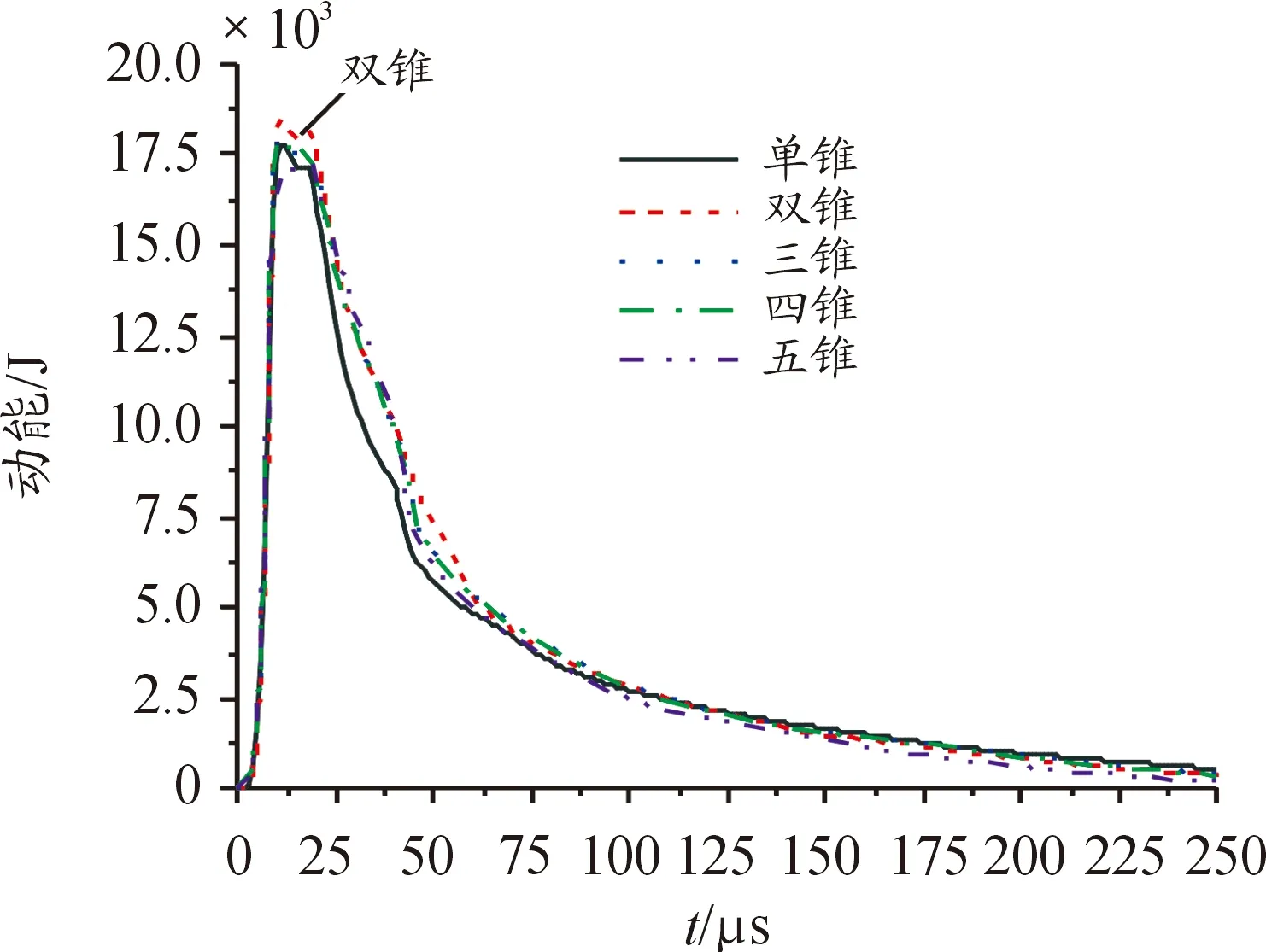
图5 不同锥数药型罩侵彻过程动能变化曲线
由图5可以看出,各药型罩所形成射流具有最大动能时间为12 μs,最大动能如表8所示,其中双锥药型罩所形成射流具有最大动能18 461 J,五锥药型罩所形成射流具有的动能最小,为16 978 J;在25 μs时接触靶板,开始侵彻过程,动能急剧下降,其中单锥药型罩所形成射流速度衰减最快;五锥药型罩所形成射流在侵彻后所剩余动能最低,其余药型罩动能下降趋势及剩余动能基本一致。

表8 不同锥数药型罩最大动能 J
双锥和三锥药型罩具有较好侵彻性能,随着锥数的增加,射流的侵彻性能并未得到提高,而是出现降低的趋势;当锥数增加到五锥时,形成的射流侵彻性能较双锥药型罩下降明显,说明过多的锥数对提高射流的侵彻性能并无帮助。
3.2 变锥位置对侵彻性能的影响
基于上节对多锥结构药型罩射流侵彻性能的数值模拟计算,改变双锥药型罩的变锥位置,研究不同变锥位置对射流侵彻性能的影响规律。变锥位置是指罩上锥角α与下锥角β过渡点A,如图6所示。变锥位置用上下锥轴向投影之比l1∶l2表示,分别对变锥位置为3∶1、2∶1、1∶1、1∶2、1∶4的药型罩进行数值模拟。其中α=40°,β=44°。
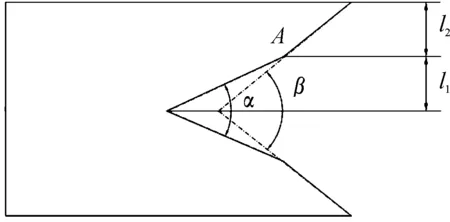
图6 双锥药型罩变锥位置示意图
对应不同变锥位置的射流侵彻深度如表9所示,可以看出,侵彻深度最大的变锥位置为方案4,方案1则与方案4侵彻深度接近,仅少0.2 mm;比值为1∶4时,射流侵彻性能急剧下降,较方案4降低13.65%。不同变锥位置药型罩射流最大速度如图7所示。

表9 不同变锥位置药型罩侵彻深度 mm
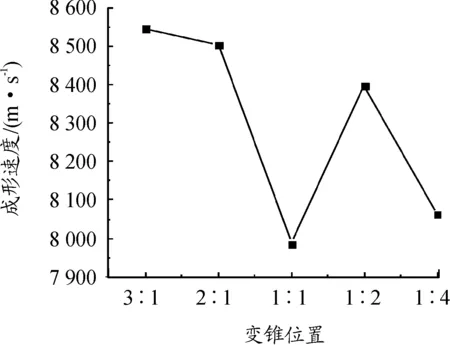
图7 不同变锥位置药型罩射流头部最大速度曲线
由图7可知,当变锥位置l1>l2时,射流头部最大速度较高,可达8 500 m/s以上;当l1=l2时,射流头部最大速度降低到8 000 m/s以下;当l1 图8 不同变锥位置药型罩侵彻过程动能曲线 由图8可以看出,各药型罩所形成射流具有最大动能时间为12 μs,最大动能如表10所示,方案1与方案2最大动能较为接近,分别为18 239 J和18 268 J,方案3、方案4、方案5最大动能较为接近均在18 465 J左右,较前2种方案有所提高;各方案在25 μs左右接触靶板,开始侵彻过程,动能急剧下降,各药型罩动能下降趋势基本一致。 表10 不同变锥位置药型罩最大动能 J 随着l1∶l2比值的变化,当比值由3∶1变化到1∶2时,射流具有的侵彻性能较为接近,而当比值变化到1∶4时,射流具有的侵彻性能急剧下降,但所具有的动能与其他方案相比稍有提高,说明影响方案5侵彻性能的因素与其他参量有关。综合侵彻深度及射流头部最大速度,可以认为当l1∶l2为1∶2时,射流具有最好的综合性能。 双锥药型罩及三锥药型罩具有较好的侵彻性能,随着锥数的增加,射流的侵彻性能并未随之提高,当锥数增加到五锥时,射流侵彻性能较单锥药型罩显著降低;采用双锥或三锥药型罩,可以提高射流的侵彻性能。在双锥药型罩中,随着下锥占比的增加,射流的侵彻性能并无较明显的提升,当上下锥比例达到1∶4时,射流侵彻性能显著降低;综合侵彻深度和射流头部最大速度考虑,双锥药型罩变锥位置应放置在l1∶l2=1∶2处。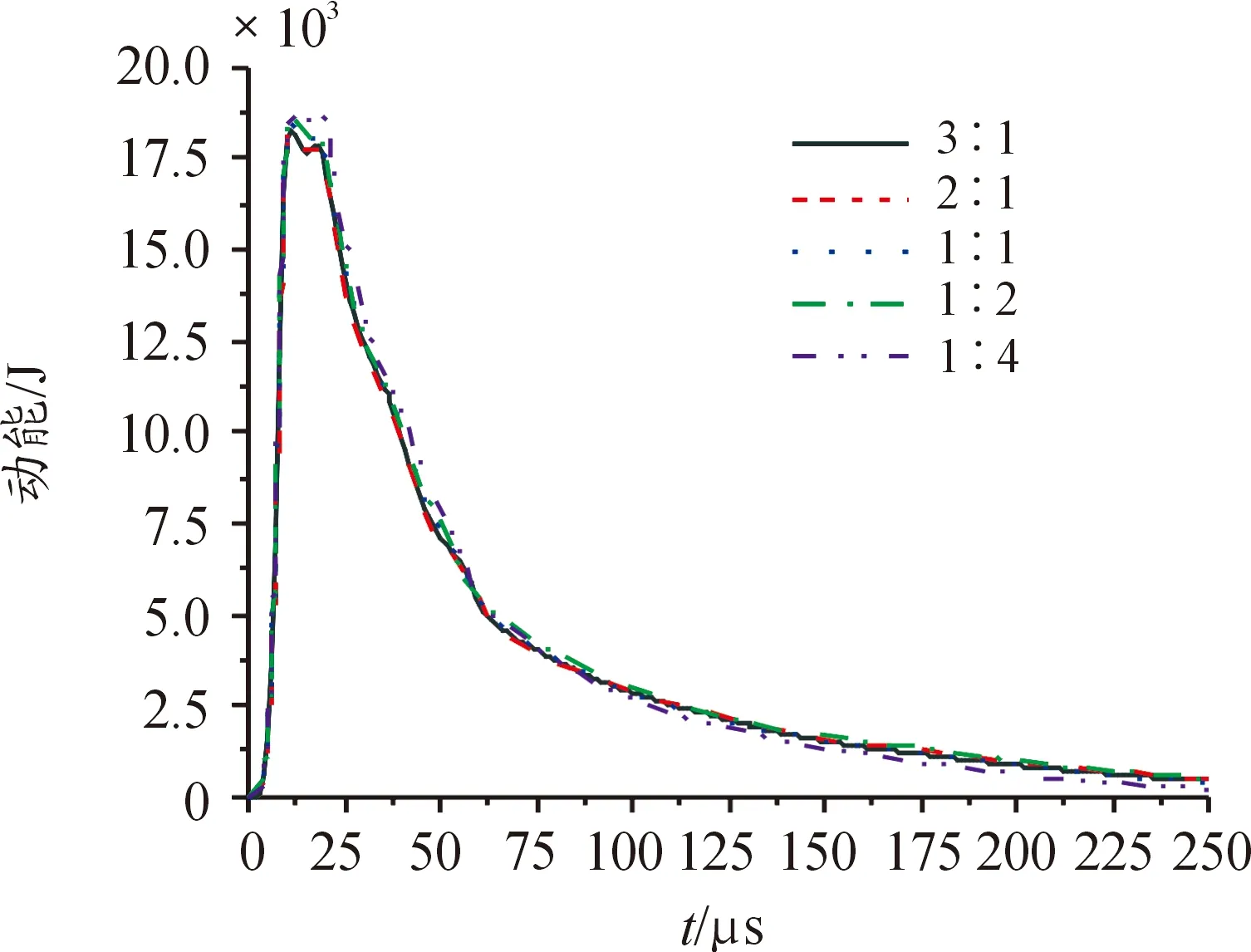

4 结论

