药型罩结构对超聚能射流性能影响的数值模拟

胡晓敏，刘迎彬，胡晓艳，孙 淼，赵家骏

(中北大学 环境与安全工程学院， 太原 030051)

聚能射流的速度和质量对射孔弹的破甲性能有着直接的影响。而药型罩的结构是影响射流的形状、速度和质量的重要因素之一。因此，研究药型罩结构对超聚能射流性能的影响，对研究破甲弹等反坦克弹种、对增强我国武器装备、对提高我国在国际上的军事地位都有着及其深远的意义。

V.F.Minin等[1]首次提出超聚能射流。他采用数值模拟分析设计了多种超聚能装药结构，开拓了聚能装药模拟仿真领域的新篇章。P.Y.Chanteret等[2]研究并设计的郁金香型药型罩目前在大炸高的情况使用，产生了速度高梯度小的射流。王成等[3]利用Autodyn-2D对比分析，得出截顶加附加装置的锥形钛合金药型罩所形成的射流能够有效地提高钛合金射流的整体速度和有效射流质量分数。王淦龙[4]以截顶辅助药型罩为研究对象，利用数值模拟方法对装药结构在不同装药长径比、下形成的超聚能射流的速度和能量以及药型罩利用率进行了分析。石军磊等[5]对超聚能射流的材料进行研究，发现辅助药型罩材料密度越大，射流头部最大速度也越大，射流能量也随着变大。陈莉等[6]发现对于截顶辅助药型罩装药结构来说，选取钛和钽的材料组合优于其他的材料组合，且变换辅助药型罩的位置对射流的形成影响并不大。

本文联系各方面对超聚能射流性能的发展需要，沿着超聚能射流的探索方向继续研究。主要研究药型罩锥角及辅助药型罩厚度的改变是否会影响超聚能射流连续性及速度方面的性能，通过Ansys-Autodyn软件模拟超聚能射流，并探索其性能特点。经对比分析后得出结论，为实际实验提供数据，更好的应用于实际情况。

1 数据模拟

1.1 材料选取

炸药爆炸使药型罩被压垮形成聚能射流的过程十分复杂，为简化理论模型，作出如下假设[7]：

① 该模拟中所有物质均为连续均匀介质；

② 超聚能射流速度随射流长度线性分布；

③ 忽略其他作用力的影响，如，重力等；

④ 整个过程为绝热过程。

聚能装药结构为轴对称结构,因此采用Autodyn-2D程序进行二维计算,且只需建立1/2模型。炸药、空气域、药型罩和辅助药型罩采用Euler网格与耦合算法。在射流形成过程中，空气区域在径向边界节点上设置flow out的边界条件，初始条件设为still air。因为模型二维对称，故只需在模型对称面上施加该约束条件。本文所做的数值模拟中截顶式辅助药型罩中选取炸药为HMX(奥克托今)，状态方程为JWL状态方程，该方程能精确地描述爆轰气体产物的体积、压力、能量等特性(表1)。锥形罩材料为铝，选用Al2024T351，采用Shock状态方程和Johnson-Cook强度模型。辅助药型罩材料为铜，采用Shock状态方程和Piecewise JC强度模型。壳体材料为Steel 1006，采用Shock状态方程和Johnson-Cook强度模型。具体材料状态方程参数如表2所示。

1.2 建立模型

超聚能装药结构如图1所示。装药长度为60 mm，装药直径为40 mm，壳体厚度为2 mm，截顶间隙14 mm，辅助药型罩直径为18 mm，锥形罩厚度为1 mm，起爆方式为面起爆。各方案装药密度均不变。模拟软件建立模型如图2所示。通过改变锥角和辅助药型罩厚度，方案设计如表3所示。

2 数值模拟结果与分析

本文采用控制变量的方法，通过改变辅助药型罩厚度和锥角的大小，设计了9种方案，利用Autodyn-2D对各个方案进行数值模拟。模拟过程中，坐标原点为罩口轴线处，起爆方式为平面起爆，起爆面模型的位置坐标为(-60，8)到(-60，-8)。

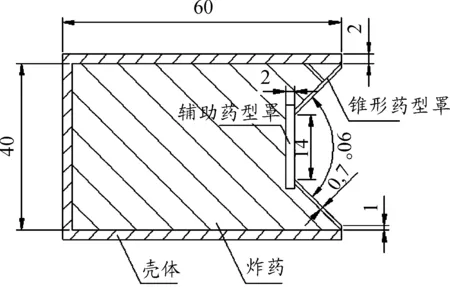
图1 超聚能装药结构示意图

图2 超聚能装药实际模型

编号辅助药型罩厚度/mm锥形罩锥角/(°)编号辅助药型罩厚度/mm锥形罩锥角/(°)116062802170736031808370426093805270

2.1 不同方案对超聚能射流形成过程的影响

图3～图5分别为方案1～9聚能装药起爆10 μs、20 μs和40 μs后的射流形态。射流长度如表4所示。表4给出了20 μs、40 μs时射流的长度。

图3 10 μs时射流形态

图4 20 μs时射流形态

图5 40 μs时射流形态

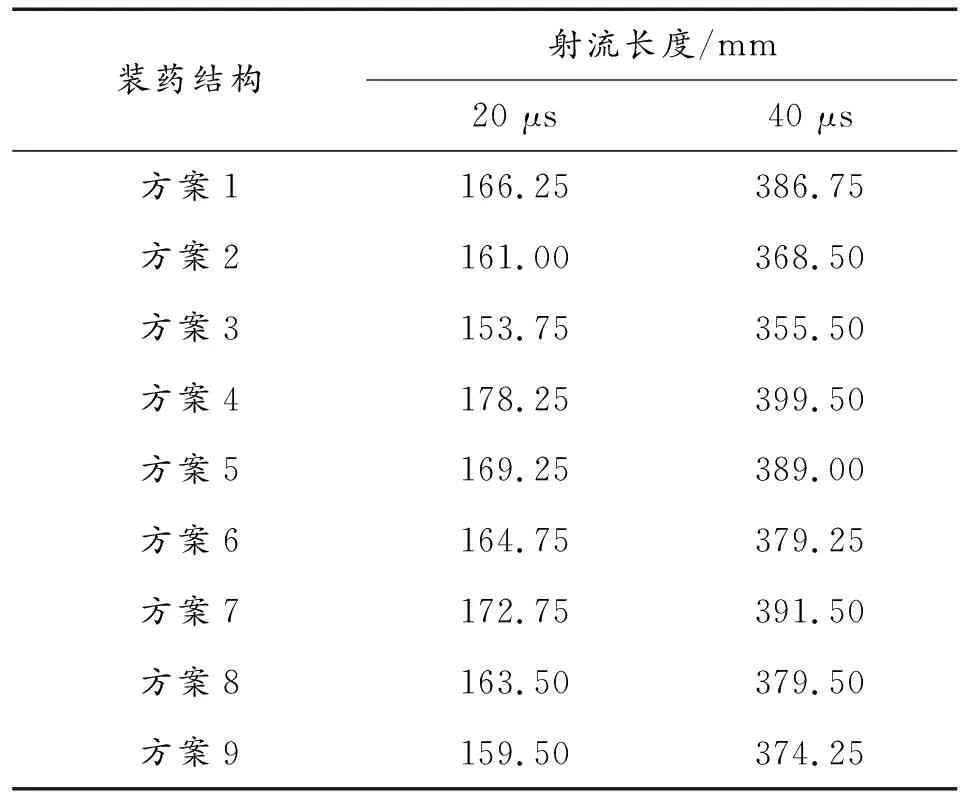
装药结构射流长度/mm20 μs40 μs方案1166.25386.75方案2161.00368.50方案3153.75355.50方案4178.25399.50方案5169.25389.00方案6164.75379.25方案7172.75391.50方案8163.50379.50方案9159.50374.25

添加辅助药型罩将给药型罩一个更强更持久的冲击压力，使罩壁微元起爆后的运动形式发生改变，压垮角度大于将180°，提高了药型罩的利用率，使射流有效质量增加。由于药型罩顶部发生翻转的同时也向中心挤压，所以超聚能射流头部速度不低于传统射流[8]。通过这种方式，我们可以实现超聚能射流模拟，并且该结构的药型罩利用率很高，甚至超过90%。不同装药结构条件下，采用变壁厚药型罩进行切割爆破切割的效果各异，要想在工程中达到最理想的效果，就要找到最佳的罩壁变化率，掌握射流随罩厚的变化规律[9]。

对于传统聚能装药结构来说，当锥角增大为110°以上时，起炸后药型罩大部分翻转，被压合成为一个直径较小的高速爆炸成型弹丸，简称EFP,不区分射流和杵体两部分。运动过程中有所拉长，直径较粗，但基本上保持完整[10]，而截顶式药型罩结构形成的超聚能射流和杵体随着锥角的增大分离的越清晰，其中射流依然为锥形。

如图3、图4所示，辅助药型罩并没有与锥形罩一起形成射流，而是同射流尾部混合在一起。起爆20 μs后，药型罩还未被完全压垮，射流头部为细锥形，杵体相对而言较少。随着起爆时间的延续，射流继续拉长后可以看出，当辅助药型罩厚度一定时，锥角越大，形成的射流长度越短。锥角为60°时，超聚能射流杵体和射流区分相对没有明确的界限，整体长度较长。当药型罩锥角为70°和80°时，超聚能射流整体长度减小，杵体和射流有较明显的界限，射流的最大直径大于杵体直径，杵体尺寸较小，形状类似细长杆。射流连续性综合观察可知，随着锥角的增大，超聚能射流的直径增大，而整体长度减小，射流的有效质量明显也减少了。当锥角一定时，随着辅助药型罩厚度的增加，射流的长度先增加后减少。

如图5所示，起爆后40 μs，射流已经出现断裂。随着锥角的增加，射流的长度逐渐减小，而杵体长度却逐渐增加，因此射流的有限质量也逐渐减小。虽然锥角为60°时射流断裂明显，但是由于射流整体长度较长，且射流直径更大，实际断裂现象并没有锥角为70°和80°时严重。当锥角一定时，随着辅助药型罩厚度的增加，射流长度先增大后增加。

2.2 不同药型罩结构对超聚能射流速度影响分析

表5给出了不同方案组成超聚能装药结构射流的头部速度。不同辅助药型罩厚度射流速度分布如图6。

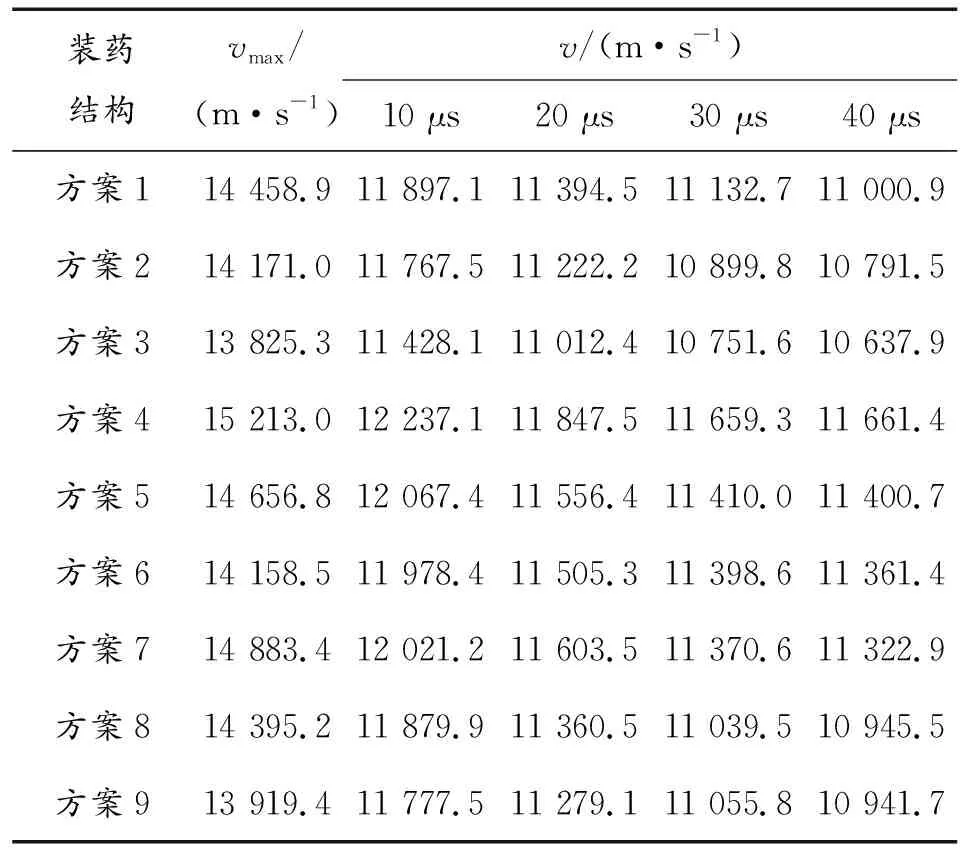
表5 不同装药结构最大速度及射流头部速度在不同时间所测结果

图6 不同辅助药型罩厚度射流速度分布

由表5和图6可知：当截顶间隙不变时，随着药型罩锥角的增加，超聚能射流的最大速度有逐渐减小的趋势。对比锥角为60°和80°的两个药型罩，其最大头部速度之间相差7.5%，这一药型罩锥角变化引起的最大速度变化差异同传统射流相似。药型罩锥角为80°时，最大速度仍然超过10 000 m/s，明显大于传统装药射流的头部速度。不同锥角形成射流头部速度相差不大，其中药型罩锥角为60°形成的射流头部速度最大，为15 213 m/s，且速度下降趋势最为迟缓。

当药型罩锥角不变时，随着截顶间隙的增加，射流的最大头部速度呈现先减小后增大的趋势。其中截顶间隙为1 mm，锥角为80°时形成射流头部速度最小，为13 825.3 m/s，但仍远远大于传统聚能装药射流的头部速度。

2.3 不同药型罩结构对超聚能射流能量影响分析

图7、图8分别给出了超聚能射流不同时刻的能量分布和不同方案组成超聚能装药结构形成的最大动能对比。

药型罩在爆轰波的作用下被压垮而形成聚能射流，此过程将会释放很大的能量，目标在高速高能的射流侵彻下毁伤将会更严重。由图7可知：超聚能装药在起爆后10 μs前均有很高的动能，但随即大幅度降低。如图8所示，随着锥角的增大，超聚能射流具有的最大能量反而随之减小。综合分析头部速度及动能，对比发现，锥角为60°、辅助药型罩厚度为2 mm的药型罩形成的射流有效质量最多，且射流最大头部速度最大的同时，拥有最大的动能。由此可知在其他条件一定时，锥角为60°、辅助药型罩厚度为2 mm的药型罩形成的射流毁伤效果更好。

图7 超聚能装药不同时刻射流能量分布

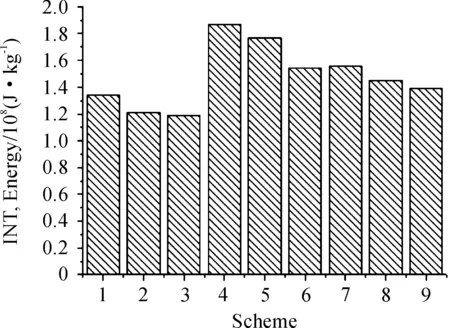
图8 不同方案组成超聚能装药结构射流的最大能量

3 结论

1) 超聚能装药结构形成的射流形态比较细长，在其他条件一定的情况下，随着锥角的增加，超聚能射流长度越短，杵体越多，射流有效质量越少，连续性也越来越差。在不同辅助药型罩厚度的情况下，随着厚度的增加，射流长度呈先增加后减少的趋势，射流连续性变化不大。

2) 超聚能装药形成的超聚能射流头部最大速以及速度减小的趋势也与药型罩结构有关。随着锥角的增加，射流头部最大速度逐渐较小；随着辅助药型罩厚度的增加，速度先增大后减小，但总体相差不大。其中当锥角为60°，辅助药型罩厚度为2 mm时，射流头部速度最大且下降趋势最为缓慢，为15 213 m/s。

3) 超聚能射流的最大动能随着药型罩锥角增大而减小。当辅助药型罩厚度为1 mm、2 mm和3 mm时，厚度为2 mm时对应的聚能射流的最大动能最大。