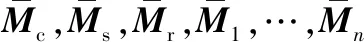基于最小动态传动误差波动量的斜齿行星轮系齿轮修形研究

张 俊, 陈 涛, 汪 建

(福州大学 机械工程及自动化学院，福州 350112)

动态传动误差直接影响齿轮装置的振动特性。动态传动误差的波动越大，齿轮振动越剧烈。因此，可通过减小动态传动误差的波动量来抑制齿轮系统的振动与噪声[1]。减小动态传动误差及其波动量通常有两类方法[2]：①提高齿轮制造和安装精度；②对齿轮进行合理修形。基于制造成本的考量，工程中一般采用齿轮修形来实现减振降噪的目标。

齿轮的传动误差可通过求解传动系统的运动微分方程获得。Chen等[3]建立了计入时变啮合刚度与齿轮误差的直齿轮传动耦合非线性动力学模型，计算了该类传动的承载接触特性和动态传动误差。Mamla等[4]建立了斜齿轮传动的弯—扭—轴—摆耦合动力学模型，通过求解系统的微分方程获得了斜齿轮传动的动态传动误差。陈会涛等[5]采用集中参数法建立了直齿行星传动系统的纯扭转动力学模型，并将传动误差分解为确定性分量和随机分量两部分，研究了传动误差的随机分量对系统动力学特性的影响。Zhang等[6]采用集中参数法构建了考虑误差激励和刚度激励的斜齿行星轮系非线性动力学模型，通过龙格-库塔法求解行星轮系的运动微分方程，得到了行星轮系各齿轮副的动态传动误差。

基于Chen等建立的解析模型，马辉等[7]通过对比三种不同的齿顶修形曲线在不同修形量下的有载荷传动误差，获得了对应不同修形量的最佳修形曲线。陈思雨等[8]基于有限元模型得到不同齿廓修形时齿轮的啮合刚度及静态传动误差，并研究了不同齿廓修形策略对齿轮动态行为的影响。蒋进科等[9]以承载传动误差最小为目标，采用遗传算法对修形参数进行优化，获得了斜齿轮副的最佳修形齿面。Bahk等[10]采用摄动法研究了齿廓修形对直齿行星轮系振动特性的影响，并以动态传动误差波动量最小为目标函数确定了齿廓修形量。

文献调研表明，尽管可通过建立不同精细程度的动力学模型来求解齿轮传动系统的动态传动误差，但现有研究模型大多未计入齿面微观修形对系统动力学行为的影响，因而基于这些模型获得的动态传动误差的准确性有待商榷。另一方面，针对齿轮修形参数对传动系统振动特性影响的研究，大多围绕单对齿轮副展开研究，涉及行星轮系齿轮修形的研究很少，而专门针对斜齿行星传动齿轮修形的研究尚未见到。不仅如此，现有研究一般仅考虑单一的齿向修形或齿廓修形对齿轮系统动态特性的定性影响规律，鲜有同时考虑齿向/齿廓修形参数与齿轮振动特性之间定量关系的研究，更未见同时考虑内、外啮合副修形参数的研究。

有鉴于此，本文将以斜齿行星轮系为研究对象，基于齿轮啮合原理将轮齿的齿向和齿廓修形折算为齿轮副沿啮合线方向的相对位移，再将其纳入行星轮系运动微分方程，进而求解出计入微观修形效应的齿轮副动态传动误差。在此基础上，针对齿轮修形量与啮合副动态传动误差波动量之间存在复杂的非线性关系，运用响应面法建立二者之间的映射函数，据此给出动态传动误差波动量最小情况下的修形参数的优选组合，并对最终的修形效果予以评判。

1 动态传动误差的计算

不失一般性，以某风电齿轮箱的低速级斜齿行星轮系为例展开研究。该轮系以行星架输入、太阳轮输出，输入功率为750 kW，输入转速为22 r/min。其他主要设计参数如表1所示。

表1 行星轮系设计参数

1.1 轮系动力学模型

为方便表述，分别以r、c、s和pn(n=1, 2, 3)表示轮系中的内齿圈、行星架、太阳轮和行星轮。建立计入各构件3个平移自由度和3个转动自由度的弹性动力学模型，如图1所示[11]。

图1中:xi、yi、zi和uix、uiy、uiz(i=s, c, r,n)分别为各构件沿x、y、z方向的弹性变形和绕x、y、z轴的扭转变形；kix、kiy和cix、ciy分别为各构件沿x、y方向的支承刚度和支承阻尼；kju和cju(j=s, c, r)分别为各构件绕其轴线的扭转刚度和阻尼；knr、ksn和cnr、csn分别为内/外啮合副的啮合刚度和啮合阻尼。

图1 斜齿行星轮系弹性动力学模型

以平移振动位移xi、yi、zi和扭转振动位移uix、uiy、uiz构成各构件的广义坐标qi，并定义qi=(xi,yi,zi,uix,uiy,uiz)T；定义行星轮系的广义坐标向量为q=(qc,qr,qs,q1,q2,q3)T。基于牛顿第二定律，推导出行星轮系的运动微分方程如下

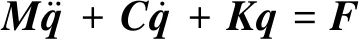
(1)

式中：M、C、K分别为系统的质量矩阵、阻尼矩阵、刚度矩阵；F为激励。

对式(1)做无量纲处理，再利用4阶变步长Runge-Kutta法可以求得未修形时系统的动态响应。篇幅所限，仅给出第1相功率流支路即太阳轮—行星轮1(s-p1)和行星轮1—内齿圈(p1-r)的动态传动误差，其结果如图2所示。为简便计，后续表述略去行星轮下标“1”。

(a) s-p动态传动误差时域图

(b) p-r动态传动误差时域图

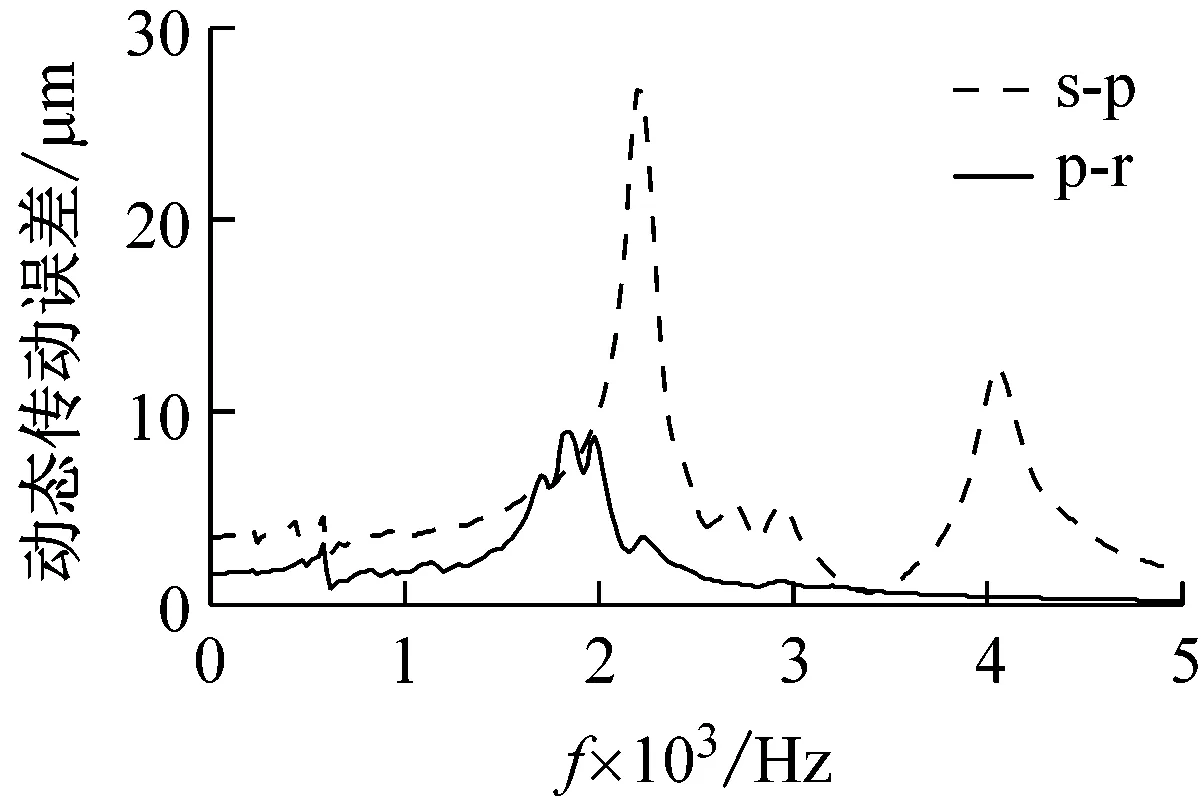
(c) s-p和p-r动态传动误差频域图

由图2可知，该斜齿行星轮系内外啮合副的动态传动误差在一个啮合周期内的波动较大；其中，s-p和p-r啮合副动态传动误差的波动区间分别为[29.42, 64.98]和[14.96, 31.08]。进一步分析其频域特性可知，动态传动误差的峰值出现在各齿轮副的固有频率及其倍频附近，内、外啮合齿轮副的动态传动误差波动量分别为8.79 μm和26.17 μm。对于高精度齿轮传动，一般要求传动误差的波动量小于4 μm。因此，需要在原始设计参数基础上对齿轮进行微观修形处理。

为确定合理的齿轮修形策略，借助Romax软件对斜齿行星轮系进行受载轮齿接触分析，以获取各啮合齿面的载荷分布状况，其结果如图3所示。

(a) s-p齿面接触载荷

(b) p-r齿面接触载荷

由图3可知，内、外啮合副在双齿啮合区其齿面接触载荷较小，而在单齿啮合区其齿面接触载荷较大，且在节点附近齿面接触载荷达到最大值。其中，s-p和p-r啮合副的最大齿面接触载荷分别为1 290.19 N/mm和994.23 N/mm。进一步观察发现，内、外啮合副的齿面接触载荷分布不均匀，存在明显的轴向偏载和啮入、啮出冲击，这也与图2所示的内、外啮合副传动误差波动量较大的现象相符。

基于上述LTCA分析结果，拟定轮系的修形策略为：齿向采取鼓形修形方式，修形中心为齿宽中心；齿廓采用渐开线修形，从小齿轮单、双齿啮合处开始，分别修至齿顶。

1.2 计入微观修形的齿面方程

由于齿顶、齿根修形的相似性，下文只介绍齿顶修形的情况。根据所采用的修形策略，建立计入微观修形的齿面啮合模型，其结果如图4所示。

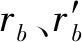
(a) 综合修形示意图

(b) 齿廓修形示意图

(2)

(3)

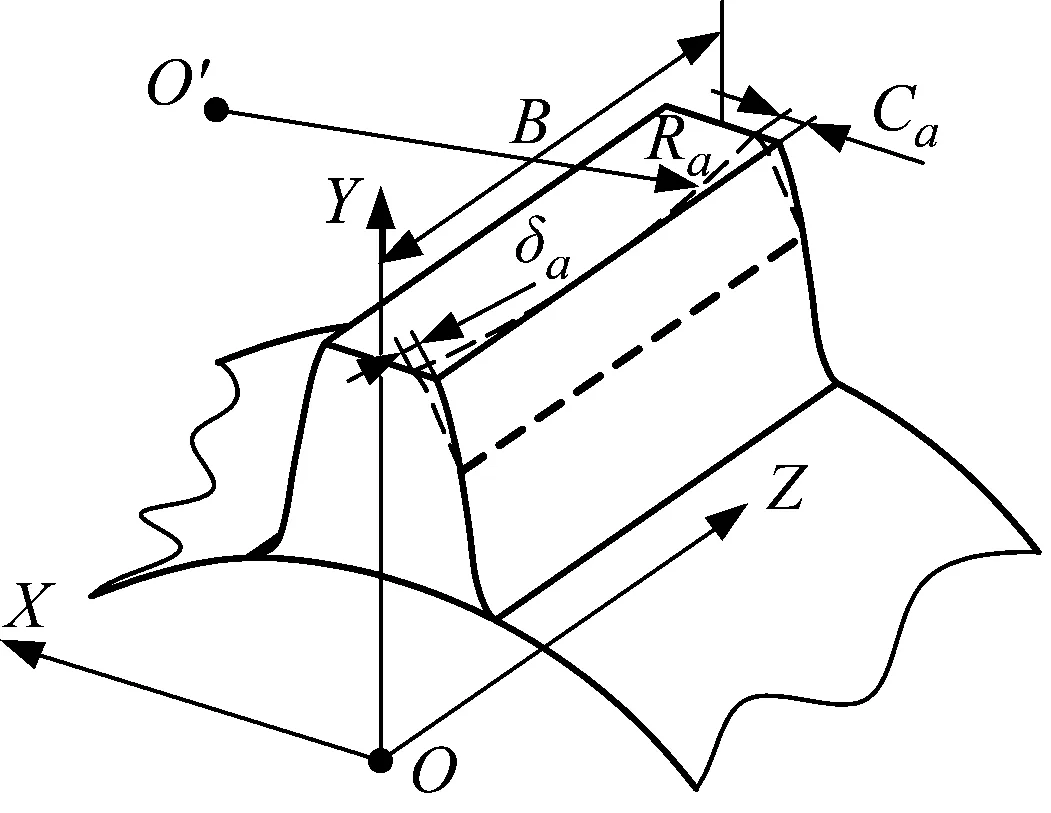
arccos(rb/ra)

(4)

(5)

由渐开线形成原理，写出未修形时的齿面方程

(6)

式中：uk为渐开线展角和压力角之和；θ为齿面上任意一点在XOY平面内绕轴线转过的角度。

计入齿轮的齿廓修形和齿向修形后，齿面方程为[12]

(7)

于是，齿轮微观修形引起的偏移量沿啮合线方向的分量h为

(8)

式中：αk为渐开线压力角。

1.3 计入齿面修形的动态传动误差计算

根据图1中太阳轮—行星轮、行星轮—内齿圈、行星轮—行星架之间的相对位置关系，引入线性坐标变换即可获得构件之间的相对位移。其中，太阳轮—行星轮和行星轮—内齿圈之间的相对位移为

δsn=xssinΨsncosβ-yscosΨsncosβ-zssinβ-

znsinβ-unzcosβ-usxsinΨnsinβ+

(9)

δrn=-xrsinΨrncosβ-yrcosΨrncosβ+zrsinβ-

znsinβ+unzcosβ+urxsinΨnsinβ-

(10)

计入齿轮修形效应后，内、外啮合副沿啮合线方向的相对位移为

(11)

式中：δrn，δsn分别为修形前内、外啮合副沿啮合线方向的相对位移，可由式(9)、式(10)计算；hrn，hsn分别为内、外啮合副的修形函数沿啮合线方向的分量，可由式(8)计算。

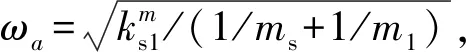
(12)

其他参数作类似处理，限于篇幅，不再赘述。

将无量纲参数和式(11)代入式(1)中，推导计入修形后的行星轮系无量纲运动微分方程为

(13)

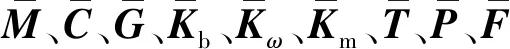
(14)

式中：ε、ζ分别为质量比例系数和刚度比例系数。

运用4阶变步长Runge-Kutta法，求解式(13)即可求得计入齿轮修形效应的系统动态传动误差。

2 基于最小动态传动误差波动量的齿轮修形

采用响应面法构造齿轮修形量和啮合副动态传动误差波动量之间的关系，并据此确定动态传动误差波动量最小时的最佳修形量。考虑到齿轮修形量与动态传动误差波动量之间复杂的非线性映射关系，构造含交叉项的二次型响应面函数

(15)

式中：y为目标拟合函数；ρ为设计变量的个数；η0，ηλ，ηλγ(λ=1,…,ρ；γ=1,…,ρ)为待定系数；xλ，xγ为响应面函数的设计变量，也即轮齿各修形量。

依据中心复合法的原则，需要做2ρ+2ρ+1次独立实验[14]。根据样本数据，利用最小二乘法求出响应面函数中的待定系数，如下式

η=(xTx)-1xTy

(16)

式中：x，y为中心复合样本点及其对应的响应值。

依据文献[15]可知设计变量的取值公式为

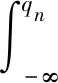
(17)

式中：qn为设计变量取值；f(q)为设计变量的概率密度函数；pn为水平点，取p1=0.01，p2=0.50，p3=0.99。

所得响应面函数一般通过复相关系数来评估拟合程度，复相关系数的值越接近1说明回归方程拟合程度越高，计算公式为

(18)

式中:SSR为响应估计值与响应均值差的平方和；SSY为响应值与响应均值差的平方和；SSE为响应值与响应估计值差的平方和。

2.1 仅对太阳轮修形时外啮合副的啮合特性

在选取样本点前首先要确定设计变量的数字特征：假设各设计变量服从正态分布，均值由式(19)来确定，标准差可取为齿距累积偏差Fp的1/6，计算结果如表2所示。

(19)

式中：cγ为齿轮综合啮合刚度；b为有效齿宽；Fm为圆周力；Fβy为啮合齿向误差；ωt为单位齿宽载荷。

表2 齿轮修形量

外啮合齿轮副修形时ρ=2，所以需9次独立实验，结果如表3所示。

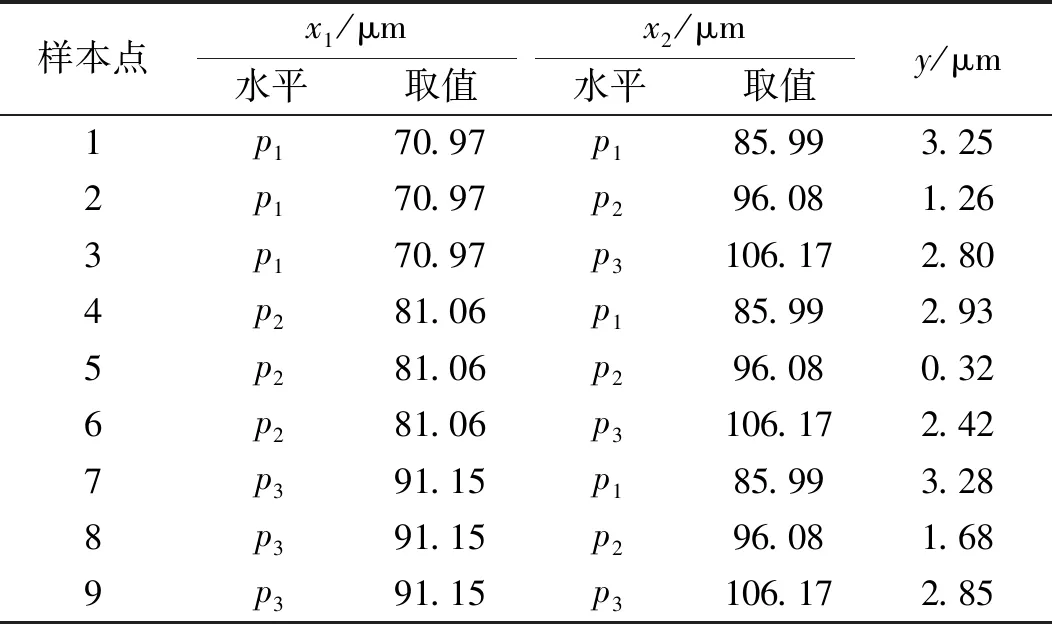
表3 外啮合副拟合函数样本参数

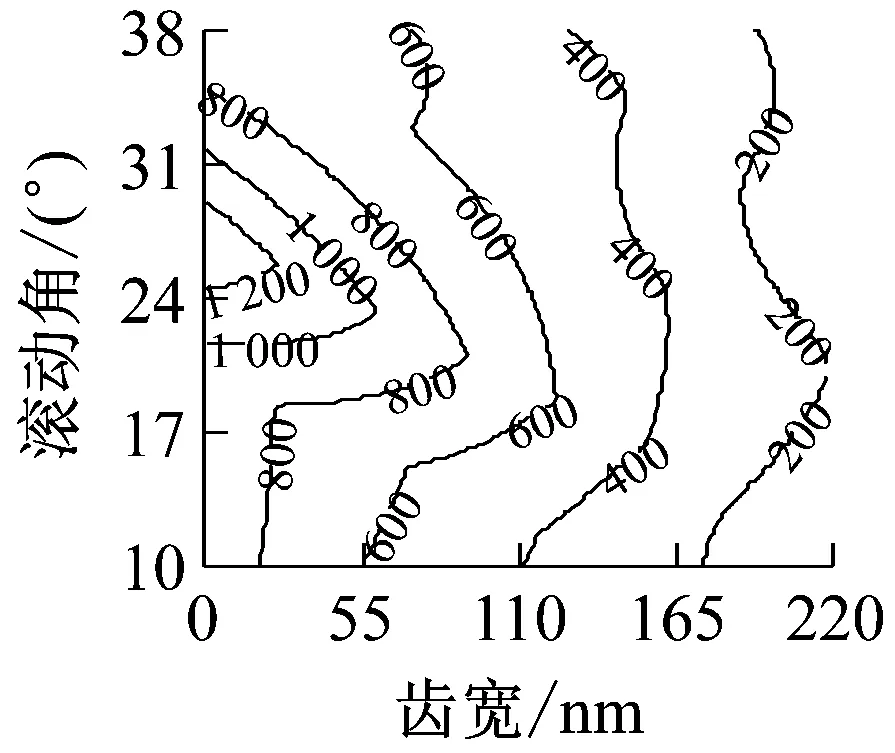
为直观计，给出太阳轮修形时齿廓、齿向修形参数与外啮合副动态传动误差波动量之间的关系，其结果如图5所示。

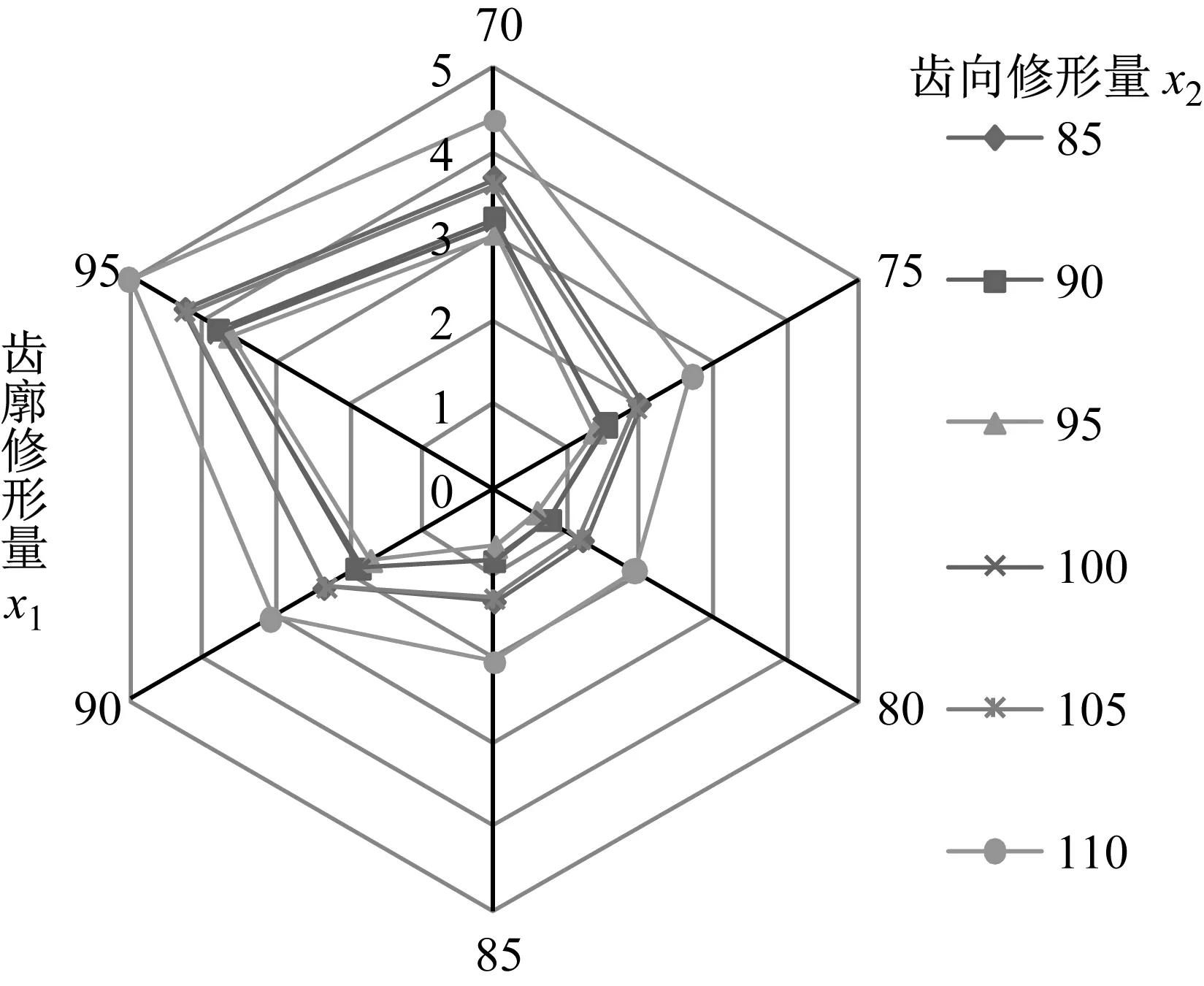
图5 外啮合副动态传动误差波动量

由图5可知，外啮合齿轮副的动态传动误差波动量随着修形量的增大先减小后增大。随着齿向修形量的增加，齿向啮合误差得到了补偿，齿面载荷更加均匀，动力学行为得到改善；当齿向修形量过大时，齿向啮合误差会产生过补偿现象，进而产生反向偏载。随着齿廓修形量的增加，齿轮副的干涉现象得到改善，啮入、啮出冲击减小，传动更平稳，使得齿轮动态特性得到改善；但过量的齿廓修形会增大齿侧间隙，在单双齿交替过程中发生撞击，进而恶化系统动态响应。

利用式(15)、式(16)求得太阳轮修形量与外啮合齿轮副动态传动误差波动量之间的响应面函数为

y=209.633 2-0.999 7x1-3.490 5x2-0.000 1x1x2+

(20)

由式(18)得回归方程(20)的复相关系数为0.976 1，说明所求回归函数对样本点的拟合程度高。由式(20)计算可得太阳轮的最佳修形量为：x1=80.23 μm，x2=96.51 μm。在此参数下，s-p副的齿面接触载荷及动态传动误差如图6所示。

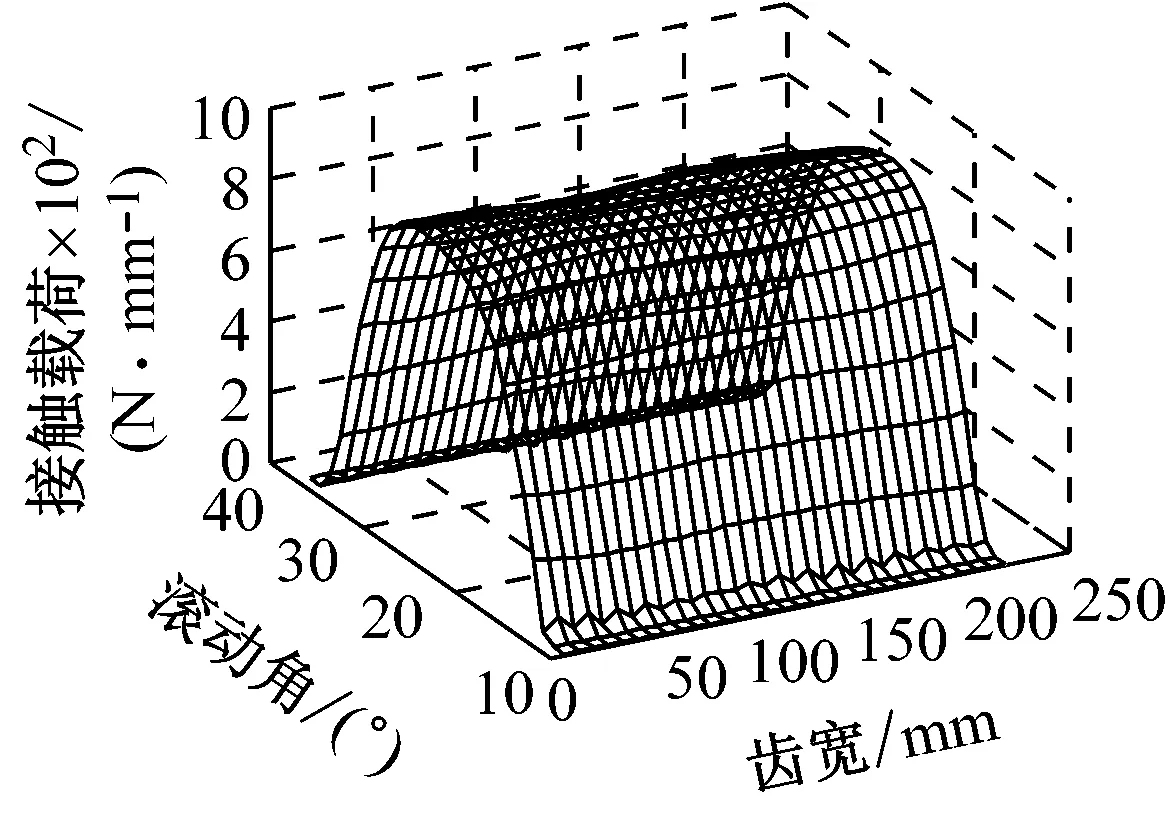
(a) s-p齿面接触载荷

(b) s-p动态传动误差时域图

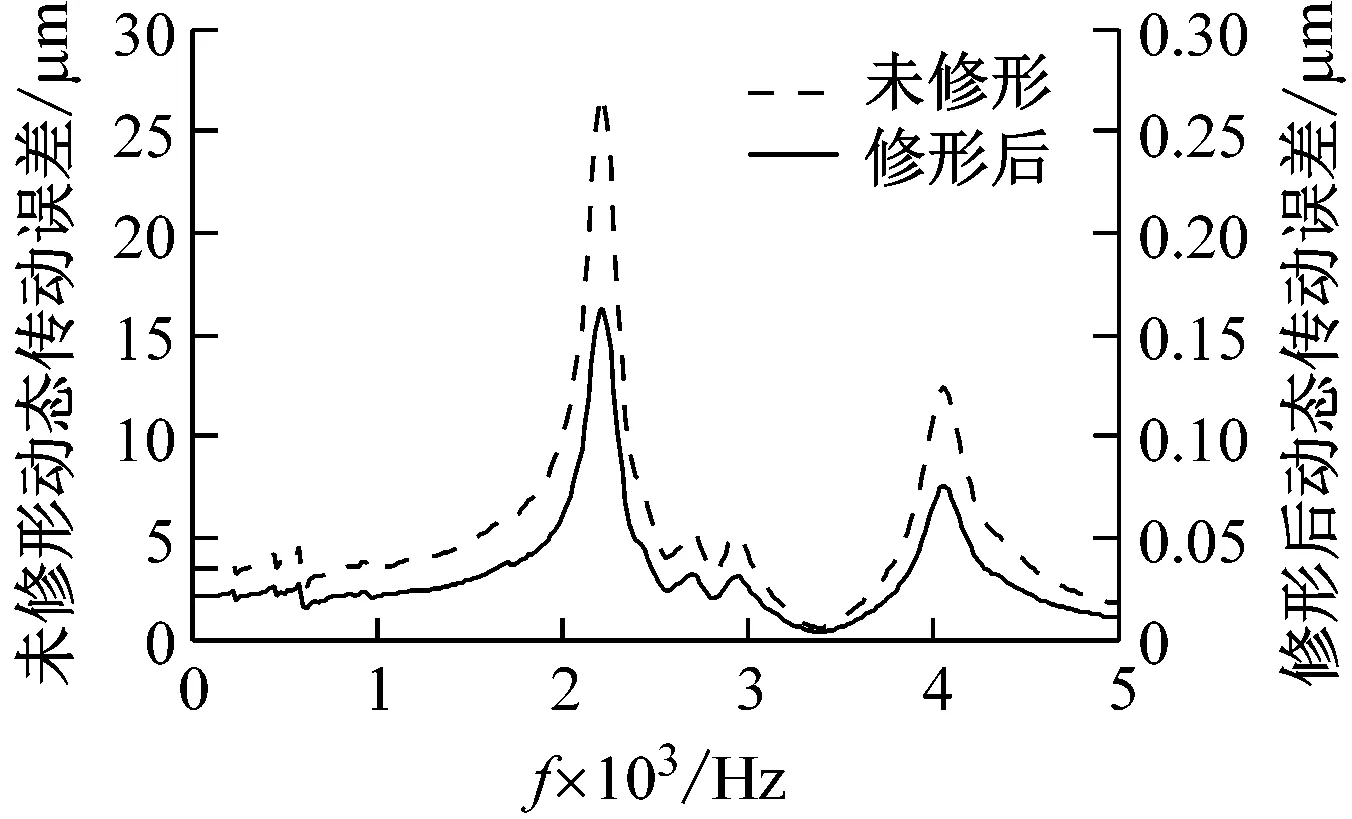
(c) s-p动态传动误差频域图

图6 太阳轮修形后外啮合副齿面接触载荷及动态传动误差

Fig.6 Contact load and DTE of external gear pair with sun modification

由图6(a)可知，仅太阳轮修形时，s-p啮合副的最大齿面接触载荷为921.61 N/mm，较图3(a)明显减小，并且明显改善了轴向偏载和啮入、啮出冲击。由图6的时域波形图知，s-p啮合副动态传动误差的波动区间为[97.02, 97.46]，且在一个啮合周期内的动态传动误差波动较图2(a)明显减小。进一步分析其频域特性可知，动态传动误差的峰值出现在各齿轮副的固有频率及其倍频附近；s-p齿轮副的动态传动误差波动量为 0.13 μm。

2.2 仅对行星轮修形时内啮合副的啮合特性

采用相同方法，可给出行星轮修形时齿廓、齿向修形参数与内啮合副动态传动误差波动量之间的关系，其结果如图7所示。

由图7可知，内啮合齿轮副的动态传动误差波动量随着修形量的增大先减小后增大。内啮合齿轮副修形影响规律与外啮合齿轮副类似，随着齿向修形量的增加，齿面载荷更加均匀，动力学行为得到改善；当齿向修形量过大时，产生反向偏载。随着齿廓修形量的增加，啮入、啮出冲击减小，传动更加平稳；但过量的齿廓修形会增大齿侧间隙，进而恶化系统动态响应。

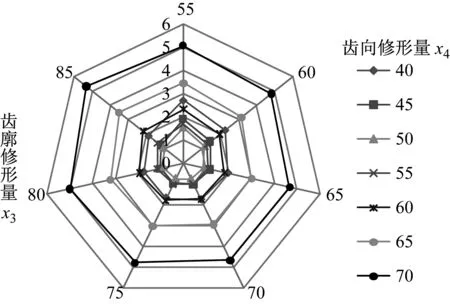
图7 内啮合副动态传动误差波动量

同理，可以求出行星齿轮修形量与内啮合齿轮副动态传动误差波动量之间的响应面函数为

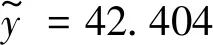
(21)

由式(18)得回归方程式(21)的复相关系数为0.984 3，说明所求回归函数对样本点的拟合程度高。由式(21)计算可得行星轮的最佳修形量为：x3=70.12 μm，x4=50.87 μm。在此参数下，p-r副的齿面接触载荷及动态传动误差,如图8所示。

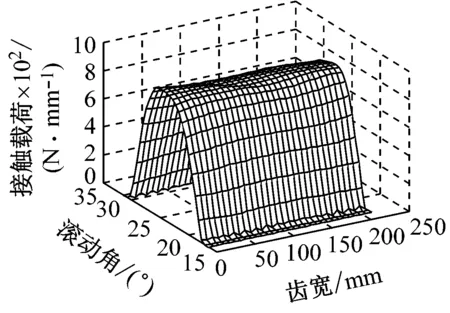
(a) p-r齿面接触载荷

(b) p-r动态传动误差时域图

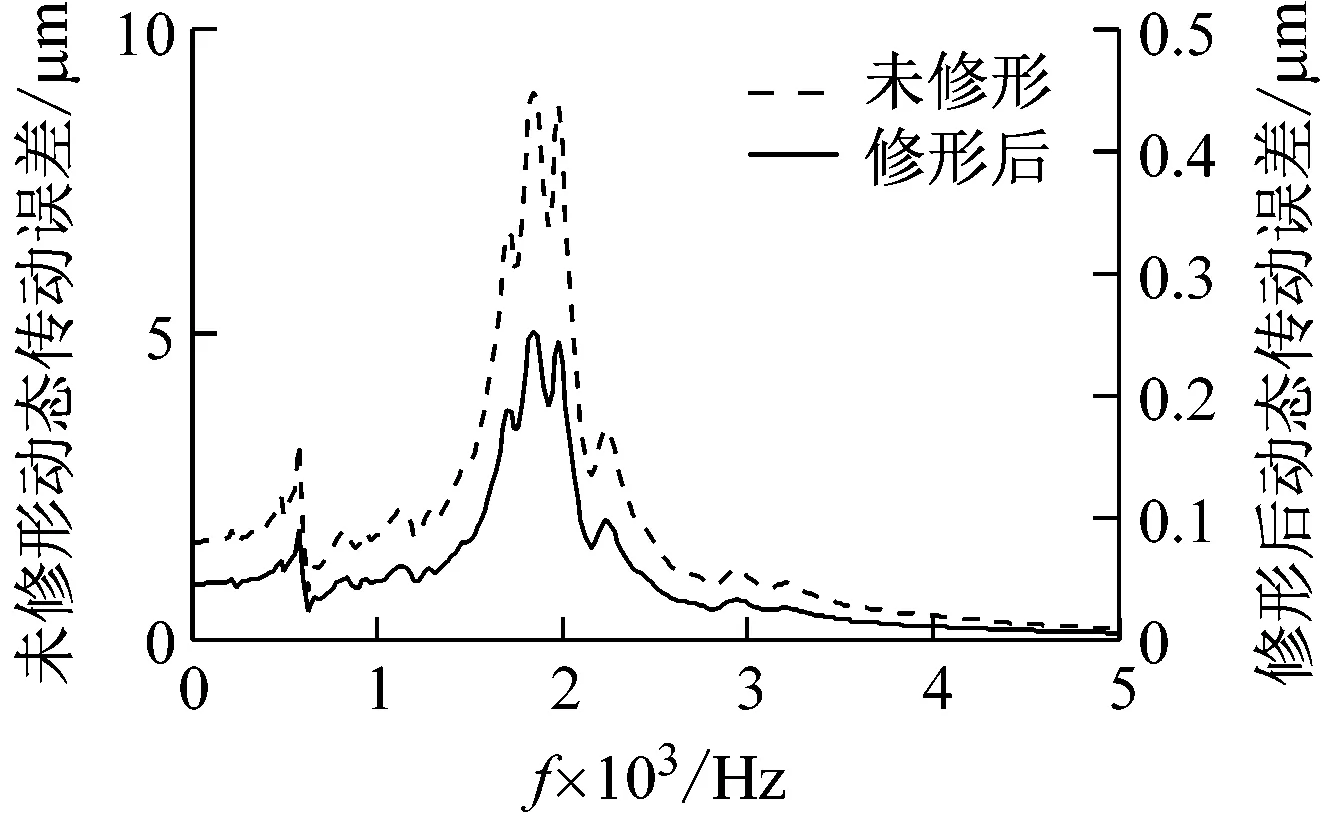
(c) p-r动态传动误差频域图

由图8(a)可知，仅行星轮修形时，p-r啮合副的最大齿面接触载荷为921.38 N/mm，较图3(b)明显减小，并且明显改善了轴向偏载和啮入、啮出冲击。由图8的时域波形图可知，仅行星轮修形时，p-r啮合副动态传动误差的波动区间为[70.11, 70.48]，且在一个啮合周期内的动态传动误差波动较图2(b)明显减小。进一步分析其频域特性可知，动态传动误差的峰值出现在各齿轮副的固有频率及其倍频附近；p-r啮合副的动态传动误差波动量为0.25 μm。

2.3 内、外啮合同时修形

以内、外啮合齿轮副动态传动误差波动量之和最小为目标，开展行星轮系的修形研究。以太阳轮、行星轮的齿廓、齿向修形量x1～x4为设计变量，构造新的响应面函数。其中，各设计变量的均值取为“2.1”节、“2.2”节对s-p、p-r副独立修形时的最佳修形量，标准差仍取齿距累积偏差的1/6。根据25次独立实验结果，求得轮系动态传动误差波动量的回归方程为

Y=96.186 5-0.734 5x1-1.429 7x2-0.018x3-0.182 6x4-0.000 7x1x2+0.000 2x1x3-0.000 1x1x4-0.000 6x2x3+

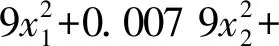
(22)

由式(18)得回归方程式(22)的复相关系数为0.994 4，说明所求回归函数对样本点的拟合程度高。由式(22)可求得最佳修形量组合为：x1=80.02 μm，x2=86.41 μm，x3=74.23 μm，x4=40.77 μm。在此参数条件下，s-p、p-r副的齿面接触载荷及动态传动误差如图9所示。

(a) s-p齿面接触载荷

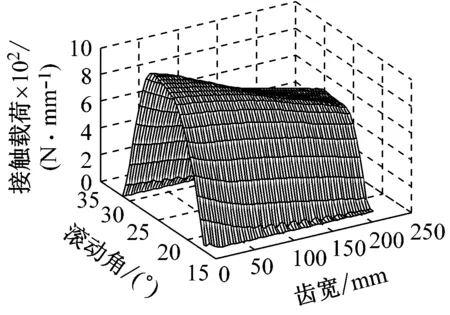
(b) p-r齿面接触载荷

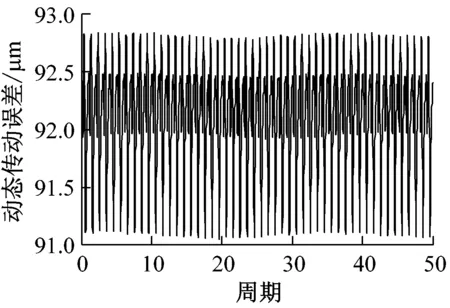
(c) s-p动态传动误差时域图

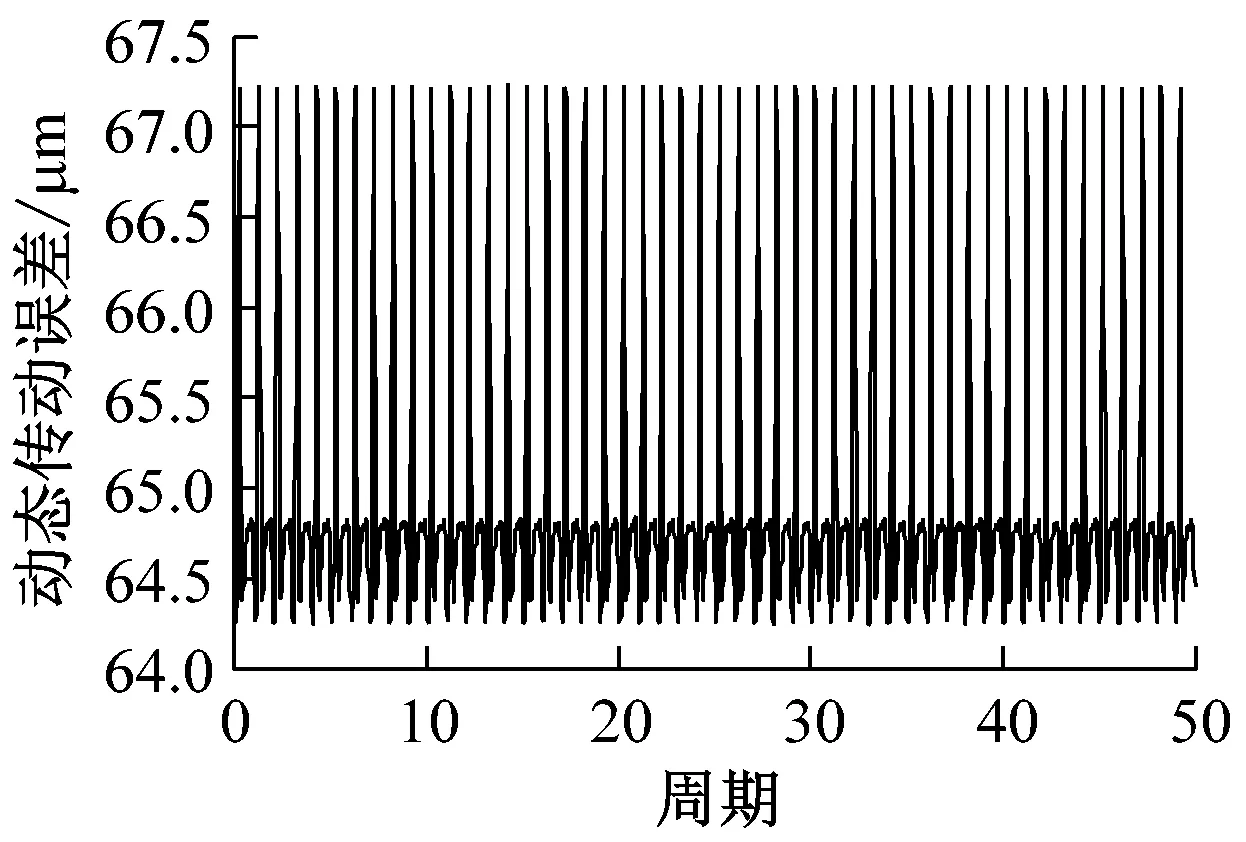
(d) p-r动态传动误差时域图

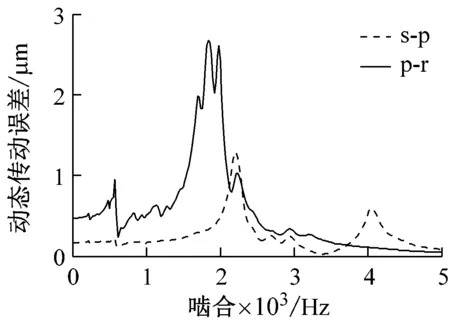
(e) s-p和p-r动态传动误差频域图

由图9的齿面接触载荷分布图可知，太阳轮/行星轮综合修形时，s-p和p-r啮合副的最大齿面接触载荷分别为921.61 N/mm和921.38 N/mm，较图3(a)、图3(b)明显减小，并且同时改善了内、外啮合副轴向偏载和啮入、啮出冲击。由图9的时域波形图可知，s-p和p-r啮合副动态传动误差的波动区间分别为[91.07, 92.83]和[64.25, 67.27]，且在一个啮合周期内的波动较图2(a)、图2(b)明显减小。进一步分析其频域特性可知，动态传动误差的峰值出现在各齿轮副的固有频率及其倍频附近；s-p和p-r啮合副的动态传动误差波动量分别为1.28 μm和2.67 μm。

采用由式(20)、式(21)计算得到的修形参数，对内、外齿轮副同时进行修形，其结果如图10所示。

由图10的齿面接触载荷分布图可知，单对齿轮副最佳修形量同时修形时，s-p啮合副的最大齿面接触载荷为951.27 N/mm，较图3(a)明显减小；但p-r啮合副最大齿面载荷为1 029.09 N/mm，较图3(b)不减反增。由图10的时域波形图可知，单对齿轮副最佳修形量同时修形时，s-p和p-r啮合副动态传动误差的波动区间分别为[90.03, 96.21]和[59.43, 70.64]，且在一个啮合周期内的波动较图2(a)、图2(b)明显减小。进一步分析其频域特性可知，动态传动误差的峰值出现在各齿轮副的固有频率及其倍频附近；s-p和p-r啮合副的动态传动误差波动量分别为1.99 μm和5.05 μm。

3 不同修形策略的效果对比

为方便比较，给出4种不同修形策略下，内、外啮合副的最大齿面载荷和动态传动误差波动量，其结果如表4所示。

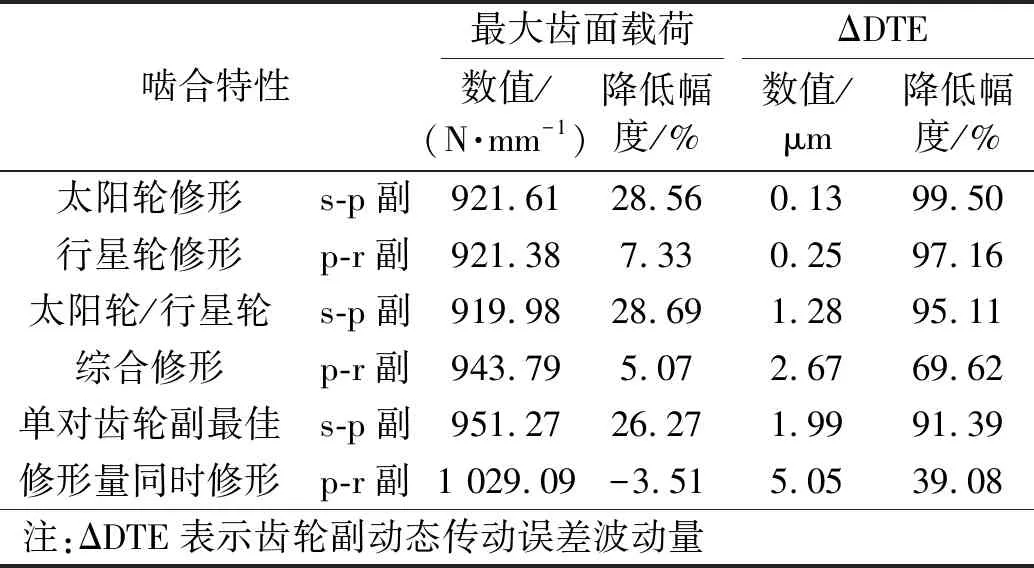
表4 修形后齿轮啮合特性

(a) s-p齿面接触载荷

(b) p-r齿面接触载荷

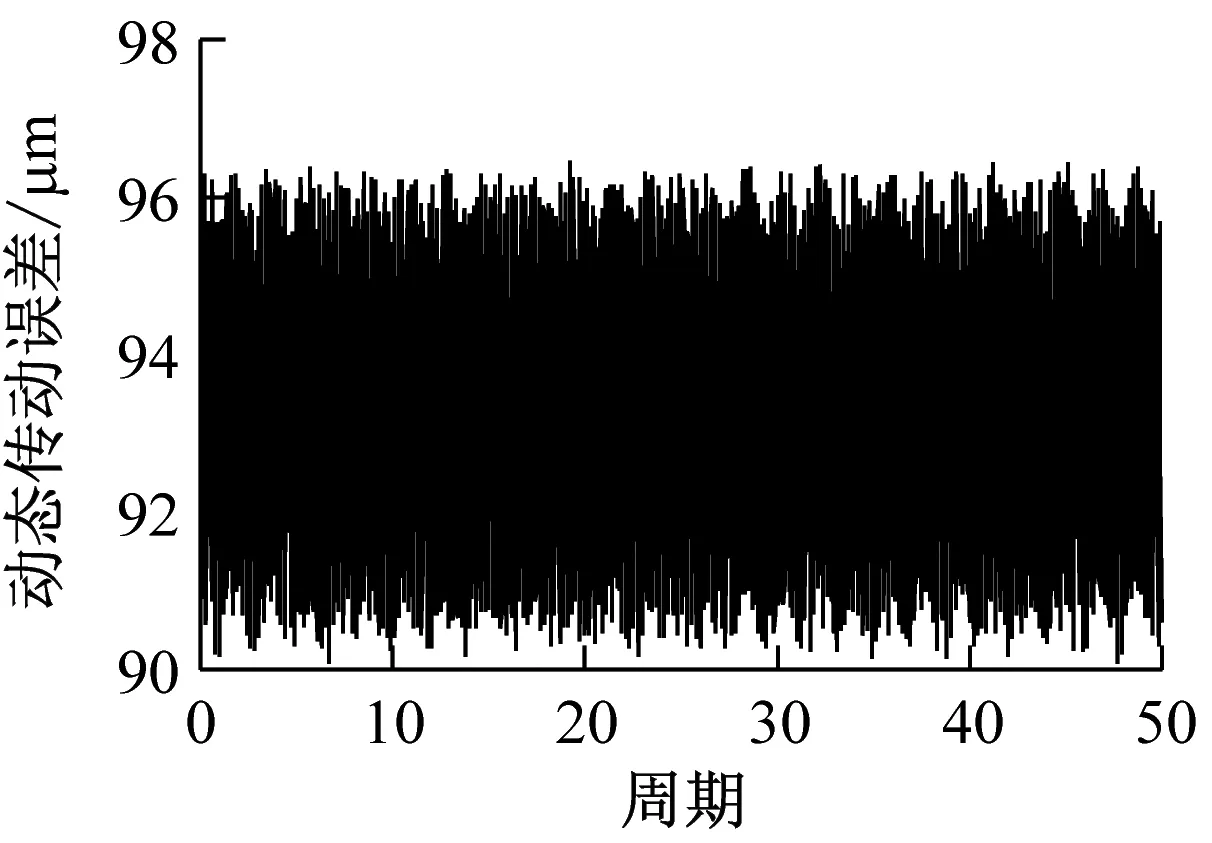
(c) s-p动态传动误差时域图

(d) p-r动态传动误差时域图

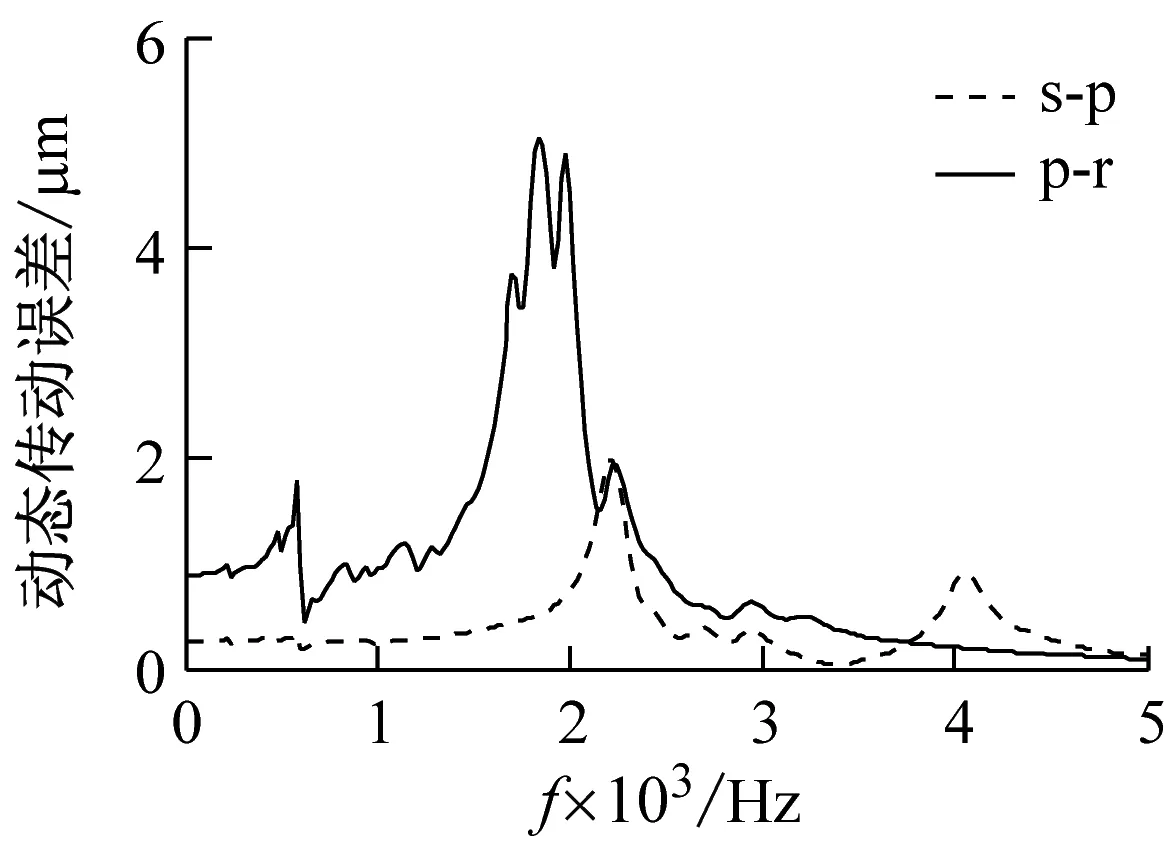
(e) s-p和p-r动态传动误差频域图

由表4可知：①单独修形和内、外啮合副同时修形时，s-p啮合副啮合特性的降低幅度都大于p-r啮合副相应啮合特性的降低幅度；②除去太阳轮/行星轮综合修形时s-p啮合副最大齿面载荷降低幅度大于太阳轮单独修形时s-p啮合副最大齿面载荷降低幅度，采用内、外啮合副同时修形策略时，齿轮副啮合特性的降低幅度都小于各齿轮副单独修形时相应啮合特性的降低幅度；③太阳轮/行星轮综合修形最大齿面载荷和动态传动误差波动量的降低幅度都要优于单对齿轮副最佳修形量同时修形。④值得注意的是单对齿轮副最佳修形量同时修形时，p-r啮合副的最大齿面载荷较未修形时有所增加，并且动态传动误差波动量为5.05 μm，超过了4 μm。

行星轮系内、外啮合齿轮副单独修形时，行星轮的运动微分方程中只考虑一对齿轮副相对位移的变化，但内、外啮合齿轮副同时修形时则需考虑内、外两对齿轮副相对位移的影响。因此以相同的修形参数分别进行单独修形和同时修形时求解运动微分方程得到的动态传动误差不会相同，进而同时修形时得到的拟合函数并不是单独修形的响应函数简单地相加。以上的原因定然使得不同修形策略时最佳修形量不会相同，从而导致了上述修形效果的不同。

4 结 论

将计入齿轮微观修形效应的行星轮系动力学模型与响应面法结合，开展了基于最小动态传动误差波动量的行星轮系齿轮修形研究。主要结论如下：

(1) 结合动力学模型计算出修形后齿轮副的动态传动误差。基于齿轮啮合原理，推导出修形函数在啮合线上的分量，将此分量视为附加的位移激励，改变修形轮齿所在的啮合副位移激励，建立了计入修形效应的斜齿行星轮系动力学模型，并依此模型计算出修形后齿轮副的动态传动误差。

(2) 内、外齿轮副的动态传动误差波动量随着主动轮齿向或齿廓修形量的增大先减小后增大。随着齿向修形量的增加，齿面载荷更加均匀，动力学行为得到改善；当齿向修形量过大时，产生反向偏载。随着齿廓修形量的增加，啮入、啮出冲击减小，传动更加平稳；但过量的齿廓修形会增大齿侧间隙，进而恶化系统动态响应。

(3) 为行星轮系综合修形提供了一种新的修形策略。同时对内、外啮合副进行修形时，以内、外啮合副单独修形时的最佳修形量为设计变量均值，构造行星轮系动态传动误差波动量与内、外啮合副修形量之间的响应面函数，并通过求解函数最小值获得轮系最佳修形量组合。

附录 行星传动无量纲动力微分方程(14)的矩阵展开式