液体火箭POGO振动分析的矢量拟合法
刘 涛, 刘锦凡, 唐国安
(1.复旦大学 航空航天系,上海 200433; 2.上海宇航系统工程研究所,上海 201109)
POGO是液体火箭飞行过程中一种常见的不稳定自激振动,是由于液体火箭推进系统与结构系统之间的耦合作用而产生,国内外众多液体火箭在飞行过程中都经历了POGO振动[1-2]。因此,POGO的抑制是液体火箭设计中的一项重要课题。
国内外学者对POGO振动开展了大量的研究工作,Rubin等[3-4]首次提出了POGO振动的传递矩阵模型,采用临界阻尼法对POGO稳定性进行了研究。由于传递矩阵模型中含有超越方程和高阶多项式,直接求解特征值十分困难,临界阻尼法近似认为POGO振动的频率为结构系统的振动频率,这种假设很大程度上降低了POGO稳定性分析的计算量,因而得到广泛应用。谭述君等[5]对临界阻尼法的适用性进行了研究,指出当结构阻尼比小于推进系统阻尼比时,临界阻尼法是适用的,反之则不适用。Oppenheim等[6]利用类似有限元的方法对推进系统的直管、蓄压器、泵等典型物理部件进行了动力学建模,进而建立整个推进系统二阶振动微分方程,实现了POGO振动的时域分析,该方法亦被称之为状态方程法。Wang等[7]针对状态方程法中矩阵不满秩给时域求解带来不便的问题,对该方法进行了改进,建立了全微分形式的POGO振动模型,提高了计算的效率。牛泽雄等[8]指出传递矩阵模型比状态方程模型更加精确,状态方程法因对管路动力学的简化描述,影响了POGO分析的精度。郝雨等[9-10]基于推进系统的传递矩阵模型,通过引入中间变量将其转换为时域动力学模型,实现了POGO振动特征值的直接求解,但该方法为保证计算精度,需引入大量的中间变量,增加了计算规模和难度,此外该方法在处理时滞问题也存在一定的不足。
针对传递矩阵模型精度更高,但由于传递函数中存在超越函数,导致特征值密集且难以直接求解这一问题,本文以某型号液体火箭为研究对象,首先建立火箭POGO振动闭环传递函数,基于矢量拟合法获取闭环传递函数的极点。进而对不同蓄压器PV值下的POGO稳定性进行分析,确定了蓄压器的设计状态。通过与临界阻尼法的对比,证明该方法具有更高的计算精度。该方法对其他液体火箭的POGO稳定性分析同样适用,具有一定的工程意义。
1 POGO振动传递函数
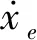
(1)
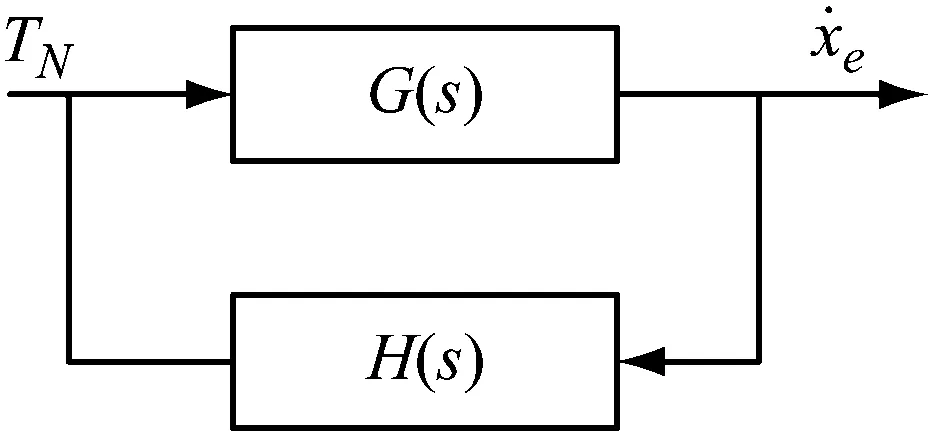
图1 POGO闭环系统原理图
1.1 结构系统传递函数
在广义坐标系下箭体结构的振动方程为
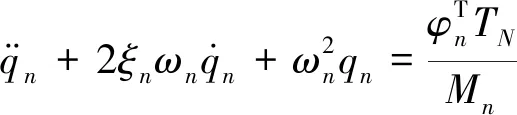
(2)
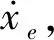
(3)
由此可得到箭体结构系统的传递函数
(4)
1.2 推进系统传递函数
液体火箭推进系统包含氧化剂系统和燃料系统,主要由输送管(直管、弯管和波纹管等)、泵、阻力元件、蓄压器和燃烧室等部分组成,如图2所示。采用模块化方法建立各部分的传递矩阵模型,该方法可以直观并且精确的描述管路元件输入输出端脉动压力与脉动流量之间的传递关系。对于直管、泵和阻力元件等部件的传递矩阵可参考文献[3]。

图2 某火箭输送系统结构示意图[11]
蓄压器安装在推进剂输送管路上,是POGO抑制最有效的措施之一,蓄压器传递矩阵为

(5)
(6)

(7)
式中:P1,P2,Q1和Q2分别为蓄压器入口和出口的脉动压力和脉动流量;P,V分别为蓄压器初始压力和初始容积;Px为发动机启动活门入口压力;K为绝热指数;Ra,La分别为蓄压器的等效电阻和等效电感。
文献[3]中将燃烧室方程的时滞项进行了线性化近似,一定程度上简化了计算,但当频率较高时,传递函数的精度会受到明显影响,本文采用的发动机燃烧室方程为
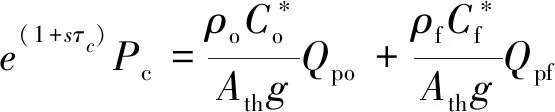
(8)

(2) 1981年年平均流量和年最大流量分别作为边界条件时,巴塘河河道纵剖面总流速与流速水头峰值出现位置基本一致。年最大流量下,河道纵剖面最末端最大总流速可达14 m/s,其他位置为0~5 m/s;年最大流量下,河道纵剖面最末端流速水头达到11 m,其他位置为0~1.5 m。年平均流量下,河道纵剖面最末端最大总流速可达9 m/s,其他位置为0~4 m/s;年平均流量下,河道纵剖面最末端流速水头达到4 m,其他位置为0~1 m。
作用在运载火箭上典型外力主要有:发动机燃烧室脉动压力引起的脉动推力,贮箱底开口处的脉动压力对结构的作用力,贮箱底开口处相对脉动流量引起的液体质心脉动对结构的作用力,泵前脉动压力和动量变化对结构的作用力。通过模态坐标转换,广义力TN可表示为
TN=NAthCφePc+AtoφtoPto+NAtfφtfPtf-NAo3φpoPso-
(9)
式中:N为发动机数量;C为发动机推力系数;ho和hf分别为氧化剂和燃料的液位高度;Ato和Atf分别为与氧化剂箱和燃料箱底部相连管路的截面积;Apo和Apf分别为泵前管路的截面积;Pso,Psf,Qpo和Qpf分别为氧化剂泵和燃料泵的泵前脉动压力和泵后脉动流量;Qto和Qtf分别为氧化剂箱和燃料箱箱底脉动流量;φto,φtf,φpo和φpf分别为氧化剂和燃料的箱底、泵前管路对应的振型。
根据推进系统各组件传递函数矩阵之间的关系,可得

(10)
式中:A和B为系数矩阵;X为各部件的脉动压力、流量等状态变量。由式可计算推进系统反馈传递函数H(s)。由于H(s)中存在时滞项和超越函数和高阶多项式,给极点的直接求解带来了极大的困难。
2 矢量拟合法
矢量拟合法是由B.Gustavsen提出的一种高效的有理分式拟合方法[12-14],能够将频域离散数据按极点-留数的形式进行拟合,由于避免了在数值拟合过程中引起的不平衡加权及病态缺陷等问题,被广泛应用于电力、控制等领域的频率特性拟合。
对于某一函数f(s),其有理分式逼近可表示为
(11)
(12)
将式中σ(s)乘以f(s)可得
(13)
式(13)为超定线性矩阵方程,将复频域离散采样值[s,f(s)]代入其中,通过最小二乘法可确定an,cn,d和h等未知量。
进一步,可将式有理分式采用零极点形式表示
(14)
(15)
通过式(14)~式(15)可得到
(16)
式(16)将求解f(s)的极点问题转化为求解σ(s)的零点问题,即从非线性问题转变为线性求解问题。
将求解得到新的极点作为初始极点再进行迭代计算,经过多个迭代步计算后可得到较为精确的极点。
3 POGO稳定性分析
将上述建模方法应用于某液体火箭的POGO稳定性分析中,选取火箭一级飞行0, 30 s, 60 s, 90 s, 120 s和150 s等6个典型秒态,研究各典型秒态下推进系统与箭体一阶纵向振动下的POGO稳定性。
图3为火箭一级飞行150 s时未安装蓄压器状态下的推进系统和推进-结构闭环系统传递函数曲线。从图中可以看出,推进系统传递函数在0~100 Hz有多个共振频率点,而推进-结构闭环传递函数有一个较为明显主共振点。
基于矢量拟合法对图3中的传递函数曲线进行有理分式拟合,由于有理分式拟合精度与式(18)的N值有关,通常N值越大,拟合精度越高,但随着N值增加,将产生大量不稳定的数学极点,影响传递函数物理极点的识别,本文引入模态辨识中的稳态图法[15]来确定传递函数中稳定的极点。稳态图法基本思路是:假定系统的阶次从Nmin到Nmax,把各阶次下的特征值计算结果画在横轴为频率纵轴为阶次的坐标图中,可得到稳定图。若每次增加阶次后,得到的极点和留数在容差范围内,则认为是相同的极点,且随着阶次的增加在稳态图中形成多个稳定轴,稳定轴所对应的极点便是系统的特征值。
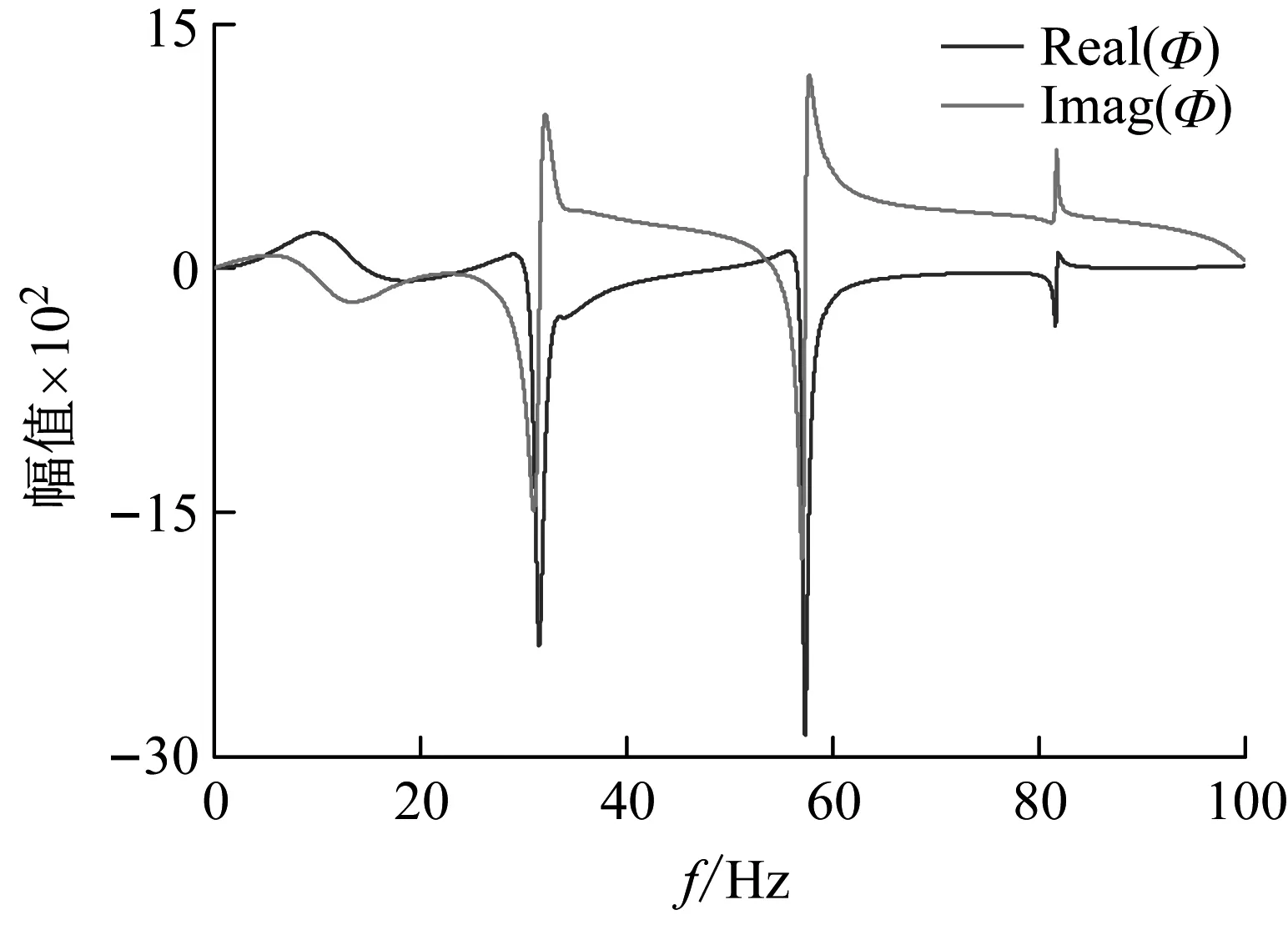
(a) 推进系统
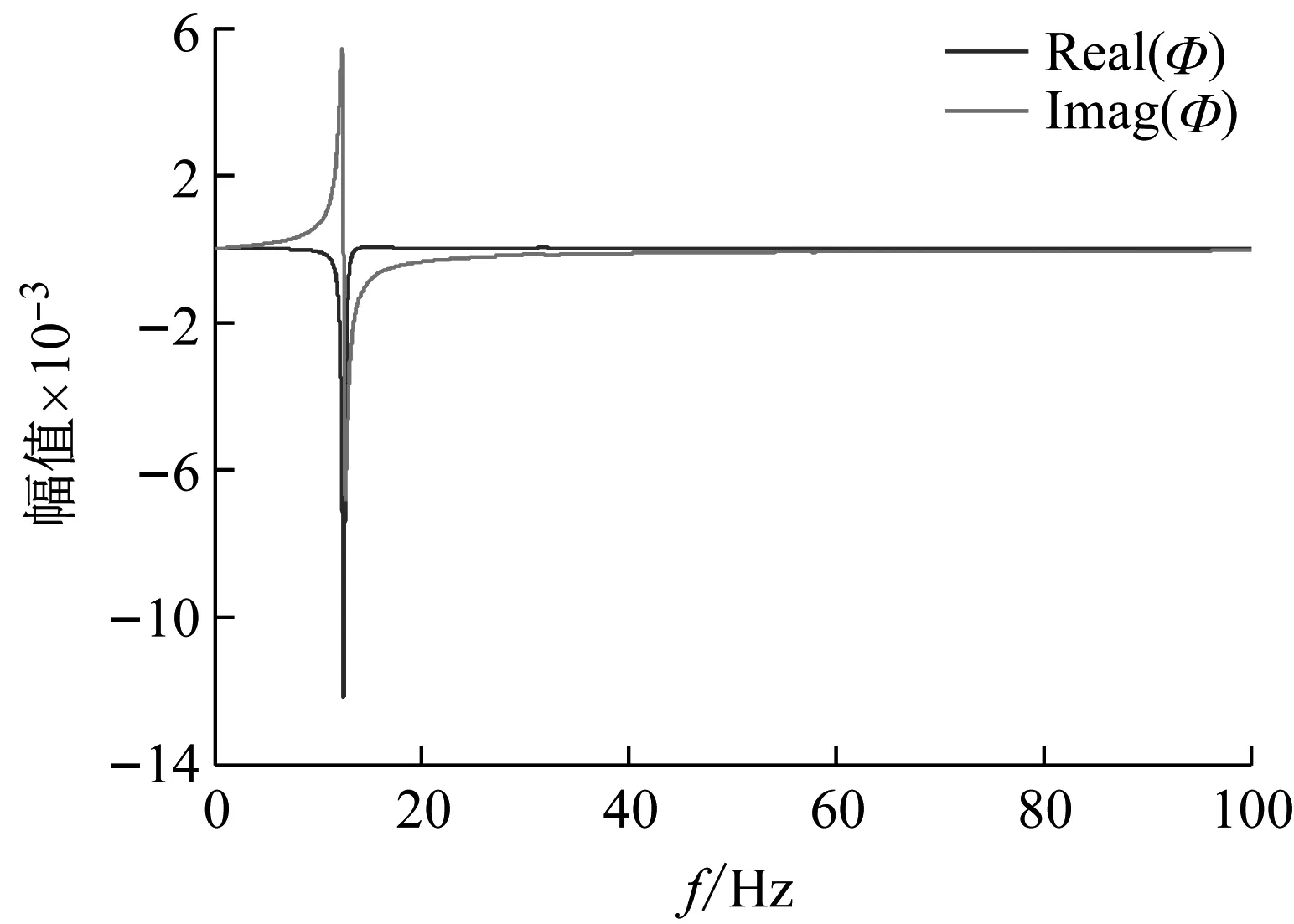
(b) 推进-结构闭环系统
图4为有理分式拟合结果,基于稳态图可以确定在0~100 Hz内推进系统有5对共轭极点,如表1所示(表中只列出正虚部的极点,表2同)。推进-结构闭环系统有7对共轭极点,前5阶极点如表2所示。表1中推进系统的一阶频率为12.57 Hz,与箭体纵向一阶共振频率12.8 Hz较为接近。由表2可知,推进-结构闭环系统一阶共振频率为12.44 Hz,对应极点实部为0.97,说明闭环系统是不稳定的,即出现POGO振动。表2中其他极点的实部均小于0,说明当箭体结构频率与推进系统频率较为接近时,容易出现POGO振动,而且POGO振动最有可能发生在箭体结构频率点附近。
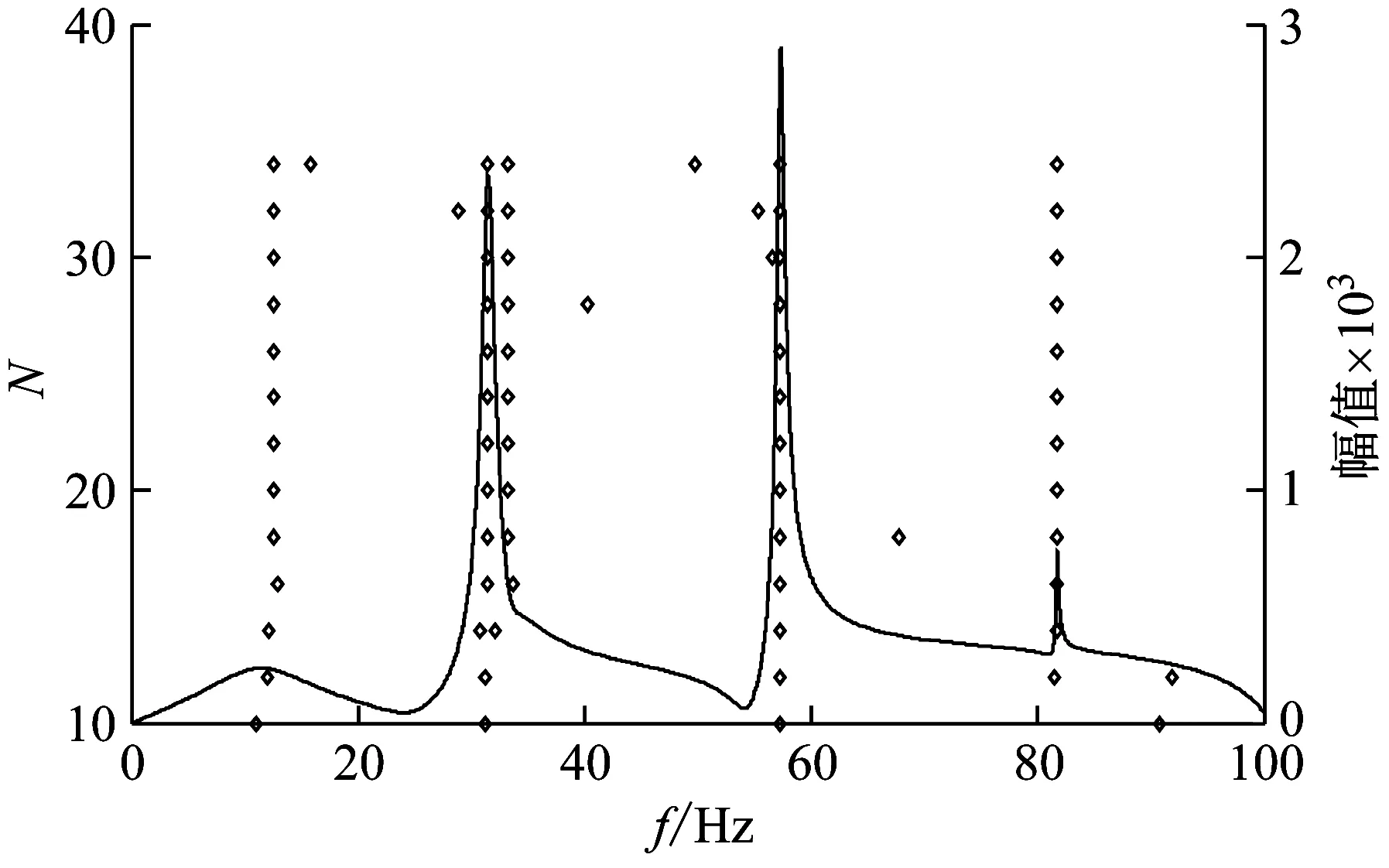
(a) 推进系统
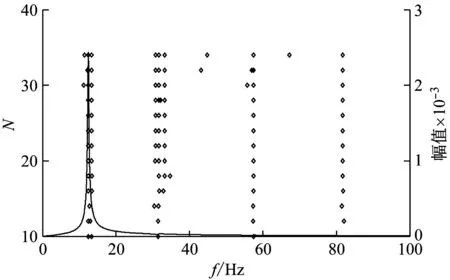
(b) 推进-结构闭环系统

表1 推进系统极点

表2 推进-结构闭环系统极点
设计上,通过改变蓄压器膜盒充气压力P和膜盒容积V来达到POGO抑制的效果。本文对蓄压器PV值在0(未安装蓄压器),0.003 92 MPaL, 0.039 0 MPaL, 0.078 4 MPaL, …,0.588 MPaL等17个状态下的POGO稳定性分别采用矢量拟合法和临界阻尼法进行分析。
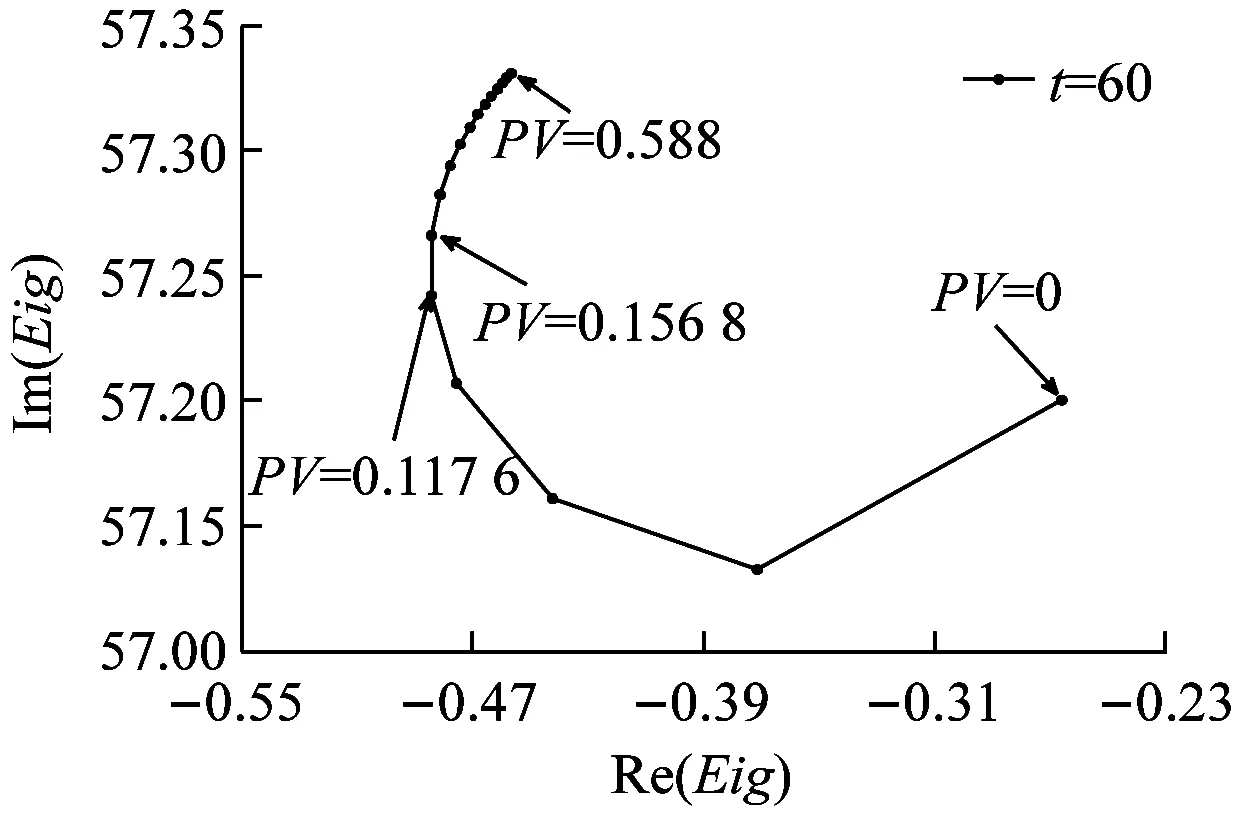
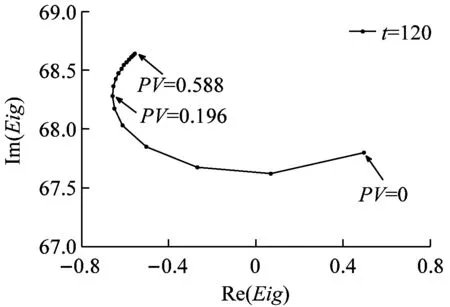
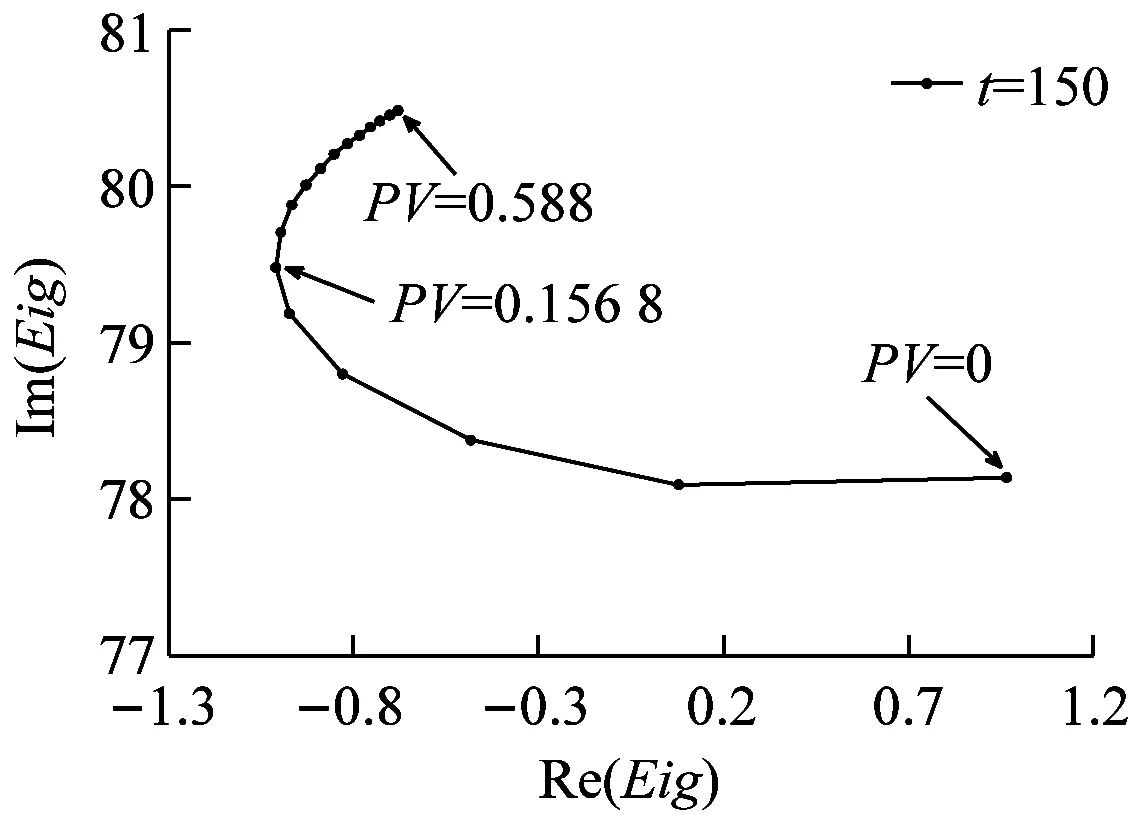
图5为各秒态下的临界阻尼值。图6为闭环传递函数在结构纵向振动频率附近的极点分布。两种方法都说明通过改变蓄压器PV值可以达到POGO抑制的效果。而且两种方法对POGO系统的稳定性的判断是一致的。但矢量拟合法可有效解决临界阻尼法的适用性问题,同时比临界阻尼法具有更高的精度。究其原因是临界阻尼法求解时近似认为出现POGO振动的点为箭体结构的共振频率点,而实际上推进-结构耦合后POGO振动的频率点有一定的改变,因此矢量拟合法的分析精度更高。
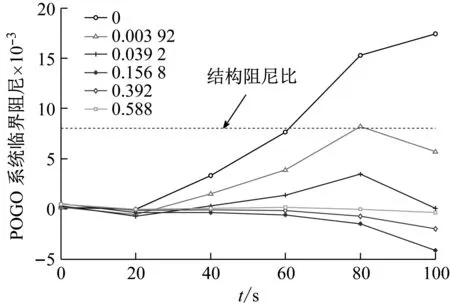
图5 各秒态下POGO系统临界阻尼值
图6表明并不是蓄压器PV值越高越好,除0外,其他秒态闭环极点实部随蓄压器的PV值均呈现先减小,后增大趋势。从图6可知,当蓄压器PV值在0.157~0.196 MPaL左右时,闭环极点的实部最小,POGO抑制效果最好。
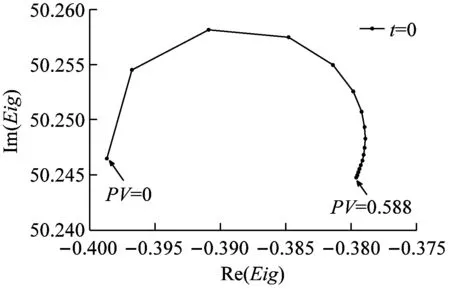
(a)
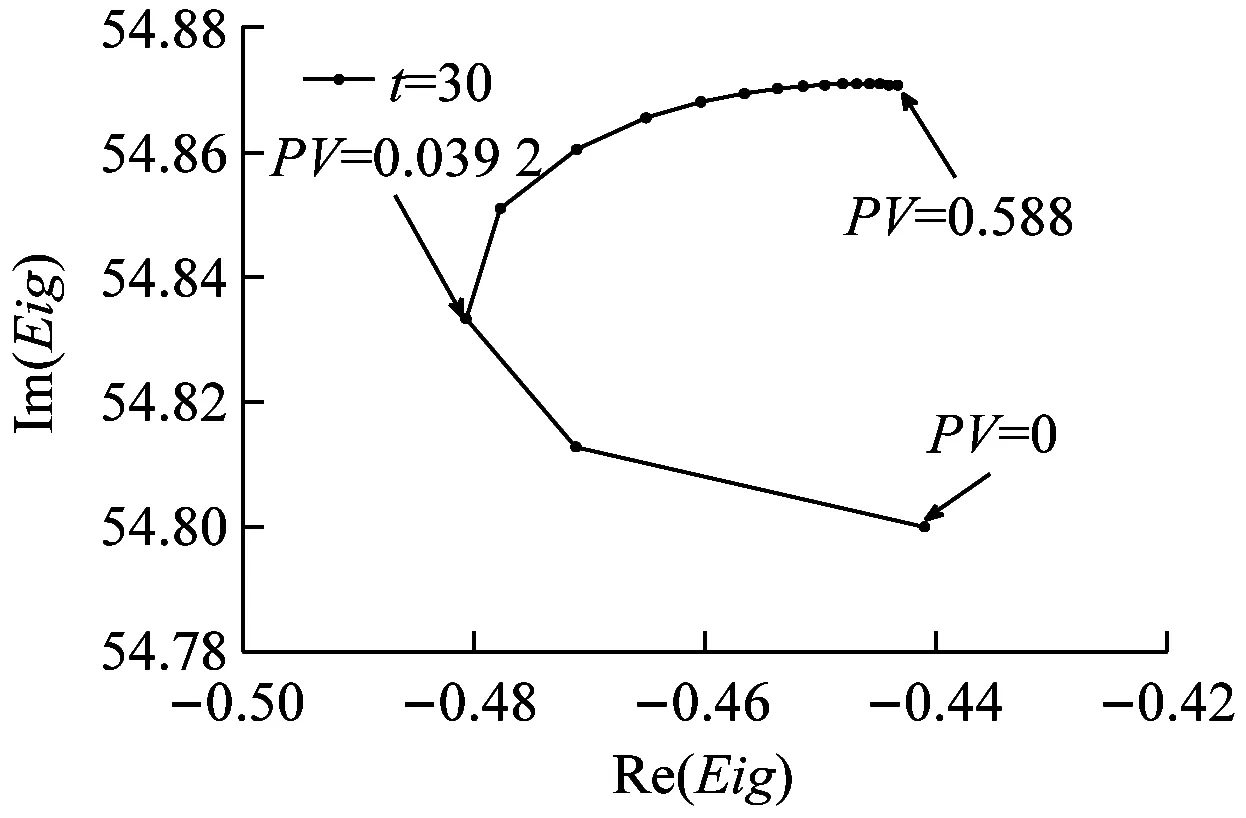
(b)
(c)

(d)
(e)
(f)
4 结 论
本文采用矢量拟合法实现对火箭推进系统-结构系统传递函数的高精度拟合,借助稳态图法可确定传递函数稳定的极点,进而通过极点实部值的正负判断POGO稳定性。通过与临界阻尼法的分析结果对比,表明矢量拟合法和临界阻尼法结论一致,但矢量拟合法具有更高的分析精度。
当推进系统频率与箭体结构频率较为接近时,易出现POGO振动,通过改变蓄压器PV值可实现对POGO振动的抑制,针对本文所研究的液体火箭,当蓄压器PV值在0.157~0.196 MPaL,POGO振动抑制的效果最好。

