ConceFT在滚动轴承瞬时转频估计中的应用

马增强， 阮婉莹， 陈明义

(1. 省部共建交通工程结构力学行为与系统安全国家重点实验室， 石家庄 050043;2. 石家庄铁道大学 电气与电子工程学院， 石家庄 050043)

基于瞬时转频估计的阶比分析方法无需安装键相装置，节省了空间及成本，是变转速阶比分析[1]的研究热点，而瞬时转频的准确估计是其成功的关键和前提。现有瞬时转频估计方法很多元，第一大类为基于相位解调法，例如：Combet等[2]采用短时尺度变换法实现回转轴瞬时转频的提取；Coats等[3]利用多级迭代法实现相位解调，提取瞬时转频信息。该类方法在转速大范围变化时，会在相邻阶次谐波之间产生交叉项，使得该方法应用受限。第二大类为基于时频分析法，例如：郭瑜等[4]将短时傅里叶变换(Short-time Fourier Transform, STFT)与峰值搜索结合，对STFT时频谱进行峰值搜索，进而对变转速电机瞬时转频进行估计，取得较好的测试效果，但由于STFT的固有缺陷使得其抗噪性较差；赵晓平等[5]提出STFT结合Viterbi算法估计变转速振动信号瞬时转频，成功应用于涡流离心机升速状态的转频估计，但Viterbi算法复杂度高，计算效率低；Urbanek等[6]对比幅值和相位的时频信息，寻找对应关系成功提取齿轮箱的瞬时转频。此外，还有很多其他转频估计算法，如：罗洁思等[7-8]、程卫东等[9]将多尺度线调频路径追踪应用于旋转机械瞬时转频提取，但该算法最大缺点是计算速度太慢，难以处理大量实验数据，很难应用于实际；Wang等[10]利用经验模态分解处理变转速信号，进而估计瞬时转频，但该方法存在模态混叠、端点效应等问题，处理复杂多分量信号时会产生较大误差。

综上所述，基于时频分析的瞬时转频估计方法原理简单，不受转速变化影响，适用范围广，更具实际应用价值，是现阶段研究瞬时转频估计的热门方法。该类算法成功的关键在于所用时频分析方法是否具备较高的抗噪性和时频分辨率，传统的时频分析方法(STFT、小波变换和Wigner-Ville分布)在时频分辨率、交叉项及抗噪性上均存在不同程度的问题，不便于直接应用于信号分析，需要不同的优化算法进行改进。现有的基于时频分析的瞬时转频估计方法中，通常所用的都是上述传统时频分析方法，很难取得满意的效果，这大大限制了此类方法的应用。笔者由此入手，将一种新型的时频分析方法——时频聚集(Concentration of Frequency and Time，ConceFT)应用其中。

ConceFT是Daubechies等[11]在同步压缩变换[12](Synchrosqueezing Wavelet Transform, SST)基础上，于2016年提出的全新的时频分析方法，该方法集合了多正交窗和SST的优点，不但保证了高时频分辨率，而且在抗噪性方面有极大改善，恰好弥补现有时频分析方法的不足，其能够胜任多分量复杂信号的处理，有着广阔的发展空间和应用前景。这一崭新的时频分析方法自被提出以来还尚未被广泛应用，本文首次提出将其联合峰值搜索算法用于滚动轴承的瞬时转频估计，着重研究算法的抗噪性能及瞬时转频估计精度，结果验证了所提方法的有效性，ConceFT联合峰值搜索能够在较低信噪比下得到瞬时转频的精确估计。

1 理论基础

1.1 时频聚集方法原理

1.1.1 同步压缩变换

同步压缩变换是从连续小波变换出发的，首先对信号进行连续小波变换，再进行时频重排，对小波系数进行压缩变换，使得时频分布更清晰、时频分辨率更高。

Daubechies以一个幅值恒定的谐波信号s(t)=Acos(ωt) 为例进行阐述。

首先求出信号s(t)的连续小波变换为

(1)

然后计算信号s(t)的瞬时频率

(2)

式中:∂bWs(a,b)为Ws(a,b)对b的一阶偏导。

通过估计出的瞬时频率ωs(a,b)可以将原来的时间-尺度平面转换到时间-频率平面：(a,b)→[ωs(a,b),b]。小波系数变为Ws(ωs(a,b),b) ，通过压缩时间-频率平面内的小波系数，将其压缩至中心频率ωl的一个邻域内：[ωl-1/2Δω,ωl+1/2Δω] ，从而得到同步压缩系数Ts(ωl,b) 。考虑计算机在计算过程中，a,b,ω均需离散化，设ai-ai-1=(Δa)i,ωi-ωi-1=Δω，则同步压缩系数可表示为

(3)

同步压缩变换相比于重排算法的优势在于其支持信号重构，根据同步压缩系数Ts(ωl,b)可以重构信号s(b)，表达式如下

(4)

对于离散参数，s(b)近似为

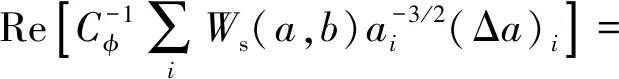
(5)

SST将时频分布沿尺度/频率方向进行压缩，从而有效提高了时频分辨率。但是，由于杂散噪声的存在使真实信号的时频分布变得模糊，时频分辨率大大降低，为此，引入多正交窗来降低噪声的干扰。

1.1.2 多正交窗同步压缩变换

在同步压缩变换的时频分布中，对于不同母小波函数，时频分布不受影响，然而噪声分布却随母小波函数的不同而不同。因为小波变换本质上就是信号与母小波函数的卷积，因此基于不同母小波函数的小波变换相互独立，恒等分布，这一特性引出了多正交窗同步压缩变换的想法。

对于信号x(t)，给定I个标准正交母小波φi(t),i=1,…,I，根据式(2)、式(3)计算出每个母小波对应的瞬时频率和同步压缩变换，多正交窗同步压缩变换即定义为各母小波同步压缩变换的平均

(6)

对大量标准正交母小波进行平均能够抵消噪声引起的时频模糊。由此认为标准正交母小波数量越多抑制噪声干扰能力越强，但是随着标准正交母小波的增多，时频分布中模糊区域增多，因此，标准正交小波数目需要设置一个平衡，这在一定程度上限制了其使用。

1.1.3 ConceFT时频聚集方法

为了克服多正交窗同步压缩变换上述缺陷，Daubechies根据同步压缩变换的非线性特点，拓展了多正交窗方法提出ConceFT方法。

步骤1选择I个标准正交母小波φi(t),i=1,…,I，使其满足良好的时频聚集性。

步骤2选择N个单位随机向量rn,n=1,…,N。

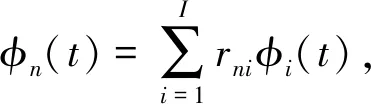
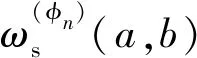
步骤5对随机向量rn做平均，得ConceFT的时频表达：

(7)

实际应用中，为了提高时频分辨率，标准正交母小波可选则2个，而为了抑制噪声干扰，权重向量N可根据需要尽可能取大[13]。

1.2 峰值搜索原理

对于一个高精度、高时频聚集性的时频分析方法，应用峰值搜索算法即可实现从时频图中准确提取瞬时频率，且峰值搜索原理简单，效率较高，故本文利用峰值搜索法实现转频曲线的提取。下面介绍峰值搜索法是如何从时频图中进行瞬时频率估计的步骤:

步骤1时频分析得时频图。

步骤2选取搜索起始点。在时频图中被跟踪分量峰值突出的区域内选择一点作为起始点。选定起始点之后，对时频图进行峰值搜索，按照下式进行

(8)

式中:ni=n1±1,n1±2,…,ni∈(0,M-1);ki∈(0,N-1);M时频网格中时间线数；N为时频网格中频率线数；IFE为峰值搜索函数；argmax为目标函数取最大值时所取参数；SPEC为对应的时频图；(n1,k1) 为以(n1,k0) 为起始点进行峰值搜索所得的第一个瞬时频率坐标；p为峰值搜索的范围；(ni,ki) 为经过峰值搜索所得的各时刻对应的瞬时频率坐标。

步骤3计算各点瞬时转频。按照下式进行

(9)

式中:fq(ni)为峰值搜索所得各点瞬时频率；q为瞬时频率对应的故障特征阶次；ni为相应的时间点。

步骤4转频曲线拟合。对上述所得离散瞬时转频进行最小二乘拟合。根据各点瞬时转频变化趋势，选择多项式次数。通常情况下，转速不会发生突变，可选择低次多项式拟合，以二次为例，拟合公式如下

(10)

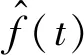
平方误差如下

(11)

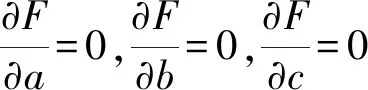
2 ConceFT估计滚动轴承瞬时转频实现过程

实际滚动轴承振动信号常伴有强烈噪声干扰，鉴于ConceFT具有强抗噪性和高时频分辨率的优点，提出了将其与峰值搜索结合用于滚动轴承的瞬时转频估计，以解决现有方法的抗噪性差及估计精度不足的问题。对于实际的滚动轴承振动信号，为了提高其瞬时转频估计精度，在进行ConceFT之前需要对振动信号进行预处理[14-16]，步骤如下：

步骤1低通滤波，避免频率混叠。低通滤波的截止频率选为降采样后频率的1/2。

步骤2降采样，凸出时频图中的转频分量，提高估计精度。按照式(12)设置采样倍数。

(12)

式中:d为降采样倍数；int为取整函数；fs为实际采样频率；fRmax为最大转频；q为搜索分量的阶次。

步骤3去趋势项，提高振动信号的信噪比。

步骤4Hilbert包络解调，得转频相关信息。

对振动信号预处理后再进行ConceFT分析，进一步峰值搜索即可提取瞬时转频曲线。本文方法估计滚动轴承瞬时转频的总体流程图,如图1所示。

3 仿真信号验证

变转速下滚动轴承振动信号为复杂的多分量信号，在不同工况会有不同的频率调制现象、不同类型的转频曲线，且伴随的强烈背景噪声会极大地影响转频曲线提取精度。本文分别设计一个线调频多分量信号和一个正弦调频多分量信号来模拟两种工况下滚动轴承的振动信号，以更好地验证ConceFT方法在估计瞬时转频曲线问题上的优势。文献[13]已证明母小波的选择对ConceFT分析效果几乎没有影响，故在仿真信号分析中，采用2个标准正交Morse小波，权重向量N取5。

图1 ConceFT估计滚动轴承瞬时转频流程图

3.1 线调频信号验证

模拟线调频的多分量振动信号，设信号瞬时角频率为

ω(t)=2.5πt+30π

(13)

则瞬时转频为

f(t)=1.25t+15

(14)

多分量线调频信号为

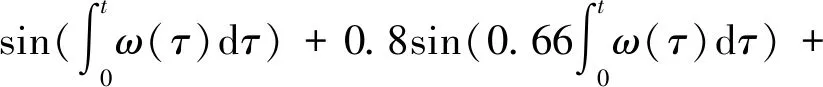
(15)

式中:η(t)为高斯白噪声；0≤t≤20 s。

该信号信噪比(Signal Noise Ratio，SNR)取为-10 dB，采样频率为100 Hz。信号波形如图2，由ConceFT所得时频图如图3所示。由图3可知，信号的一倍频、0.66倍频和0.5倍频的频率曲线，基本不受强噪声的影响。为了凸显ConceFT方法的优势，我们与经典的瞬时转频估计方法——STFT结合峰值搜索进行对比，图4为信号的STFT时频图。由图4可知，其受噪声干扰严重，各频率成分被淹没在强噪声中，难以识别。利用峰值搜索法分别对ConceFT和STFT的时频分布图进行瞬时转频提取，结果如图5所示。可见本文方法提取的瞬时转频曲线与真实转频曲线基本吻合，而基于STFT的转频估计结果偏离真实值太大。

为了定量说明两种方法的转频估计精度，利用式(16)计算估计误差的百分比值。通过计算可得，本文方法估计误差为2.56%，STFT结合峰值索搜的估计误差为52.68%。

(16)

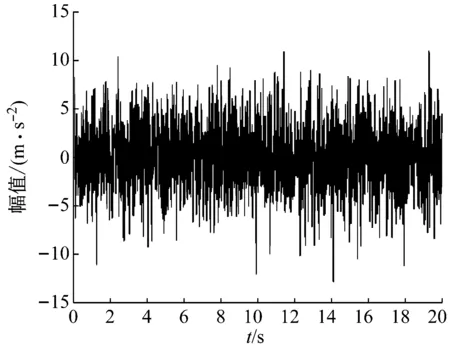
图3 线调频信号波形图

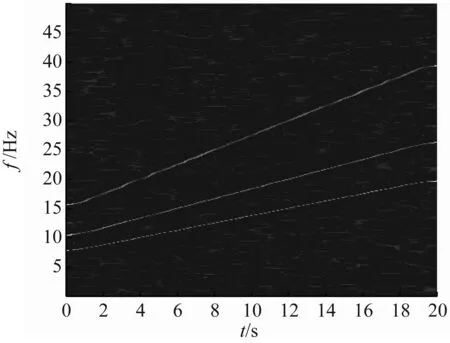
图3 线调频信号ConceFT时频图

图4 线调频信号STFT时频图

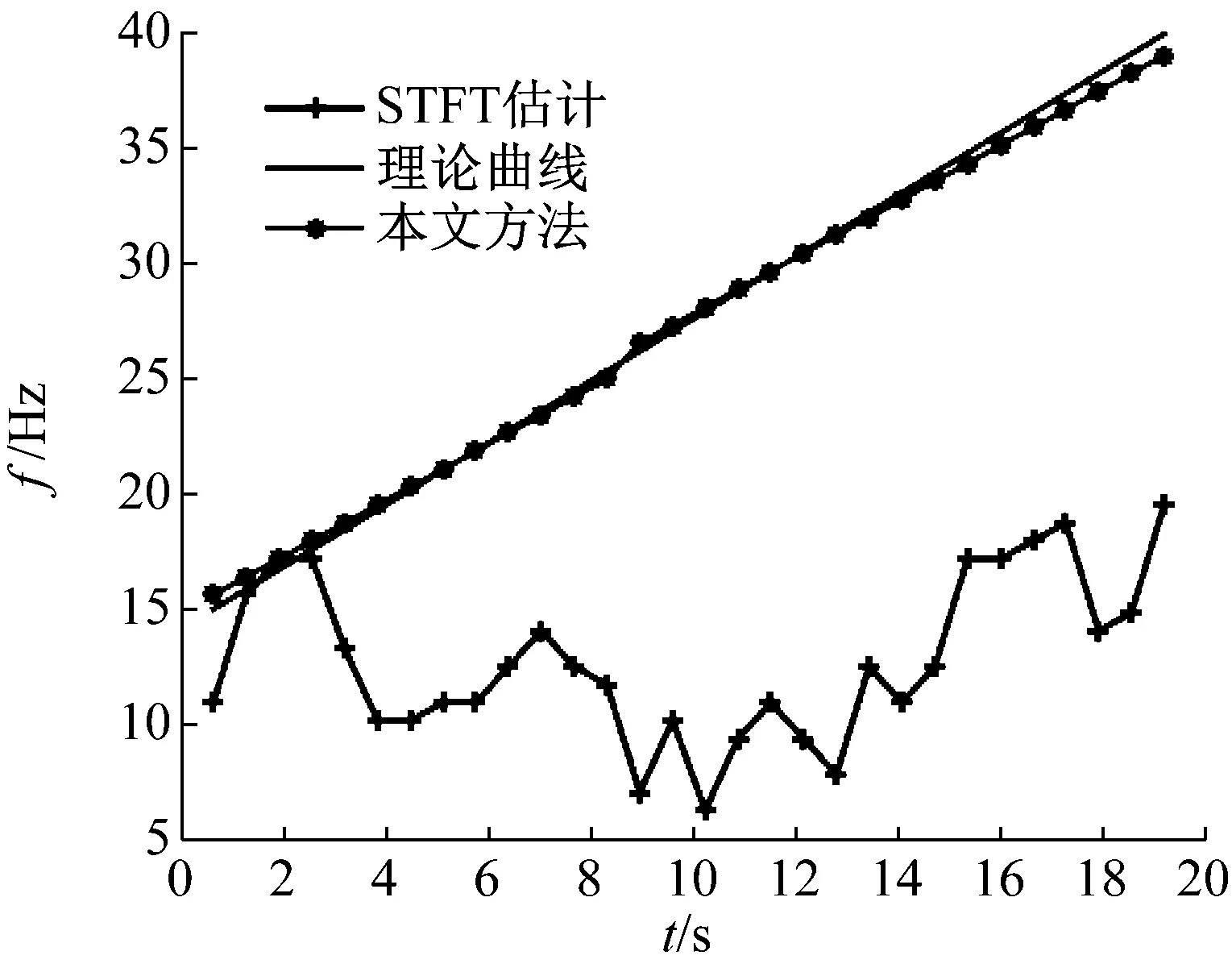
图5 线调频信号ConceFT与STFT转频估计对比图

3.2 正弦调频信号验证

模拟正弦调频的多分量振动信号，设信号角频率为

ω(t)=2π(7.5-2.5cos(t))

(17)

则瞬时转频为

f(t)=7.5-2.5cos(t)

(18)

多分量线调频信号为

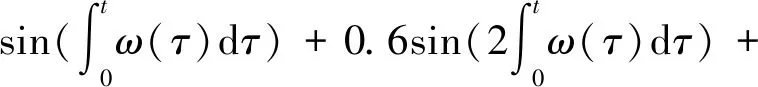
(19)

式中：η(t)为高斯白噪声；0≤t≤20 s。

信号信噪比取为-8 dB，采样频率为100 Hz，信号波形如图6所示。ConceFT时频图如图7所示，图7中三个频率分量清晰可见，而STFT的时频结果如图8所示。由图8可知，在强烈噪声干扰下，时频能量发散严重，不能识别出真实信号分量。分别对两个时频图进行峰值索搜，提取出的瞬时转频曲线如图9所示。由图9可知，STFT峰值搜索所得曲线较理论曲线波动较大，原因是信号信噪比低，部分噪声能量高于信号能量，导致峰值索搜时出现误搜索，导致最后拟合曲线出现较大偏差。由于本文方法有较强的抗噪性与高时频分辨率，能够弱化噪声影响，使频率成分能量集中，可以对其时频图进行精确的峰值搜索，所得拟合的曲线与理论曲线基本吻合。经过计算，本文方法估计误差为1.26%，STFT结合峰值索搜的估计误差为42.85%。

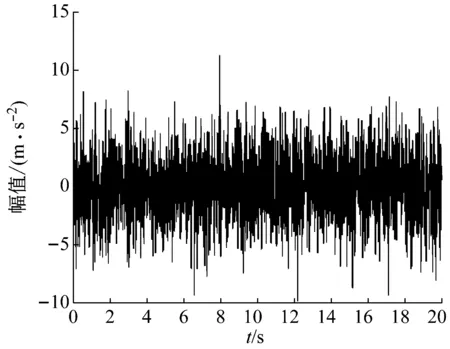
图6 正弦调频信号波形图

图7 正弦调频信号ConceFT时频图

图8 正弦调频信号STFT时频图

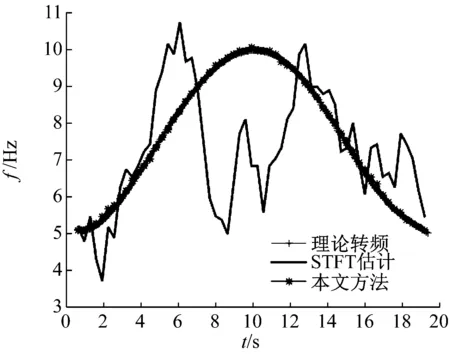
图9 正弦调频信号ConceFT与STFT转频估计对比图

Fig.9 Contrast figure between ConceFT and STFT for rotational frequency estimation of sinusoidal frequency modulation signal

3.3 抗噪性及估计精度分析讨论

在此，我们进一步分析讨论ConceFT方法的抗噪性及用于瞬时转频估计的精度问题。为了更具说服力，笔者采用大量数据进行测试。分别对上述线调频信号和正弦调频信号添加白噪声，使信号信噪比从-20～10 dB之间变化，对各状态下的信号进行基于ConceFT的转频估计工作，计算不同信噪比下的转频估计误差。

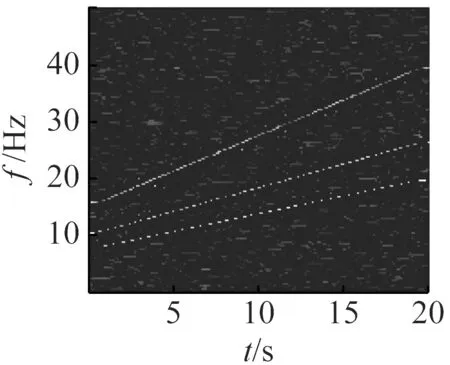
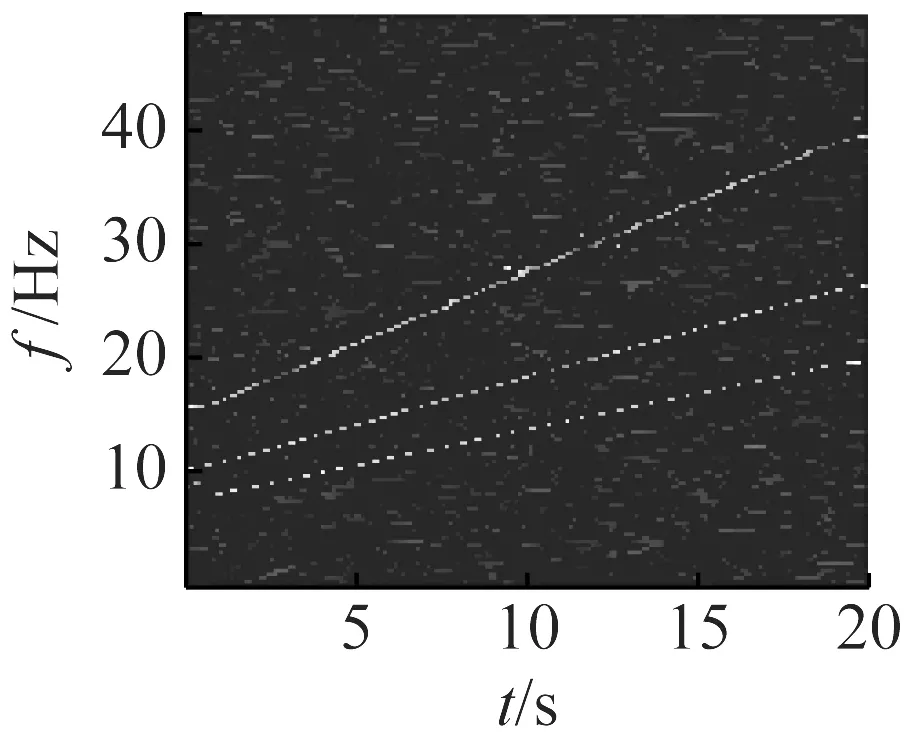
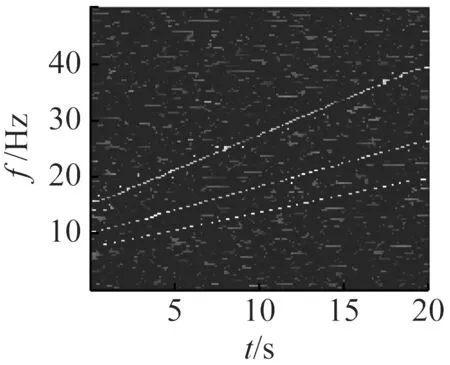
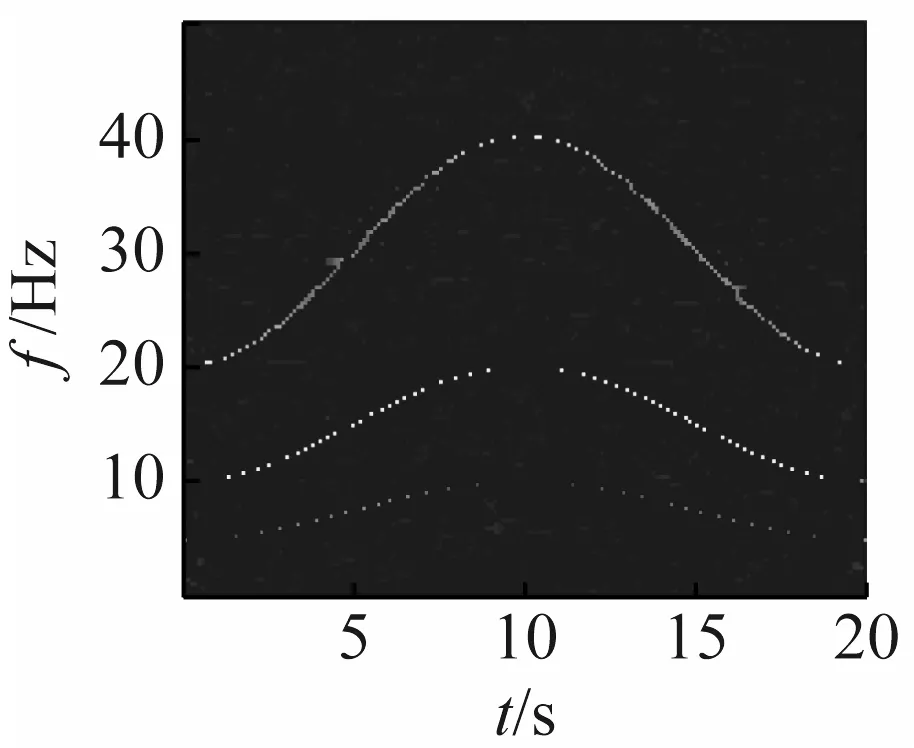
选4组典型信噪比下的信号，做ConceFT时频图，图10对应线调频信号。图11对应正弦调频信号。从两幅图中可知，在信噪比很低时，时频分辨率仍然很高，仍能清晰显示信号的瞬时频率曲线。

为了定量说明该方法在低信噪比下仍能保持高时频分辨率，采用Rényi熵作为评价指标，Rényi熵值越小表示时频分辨率越高，其定义式如式(20)所示

(a) 信噪比为10 dB

(b) 信噪比为0

(c) 信噪比为-10 dB

(d) 信噪比为-20 dB

(a) 信噪比为10 dB

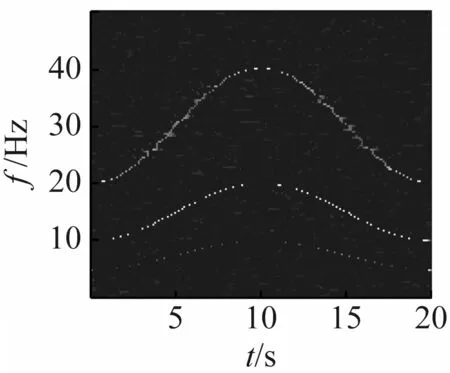
(b) 信噪比为0

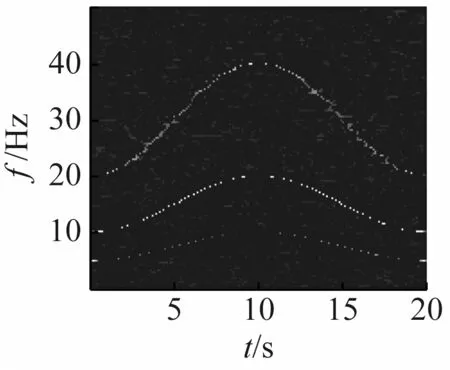
(c) 信噪比为-10 dB

(d) 信噪比为-20 dB

(20)

式中，R为Rényi熵，q≥0,q≠1,(p1,p2,…,pn)为任意离散变量的概率分布。

就图10和图11所用的4种典型信噪比下的两种信号分别求ConceFT和STFT的Rényi熵，如表1和表2所示。从表1和表2可知，两个表中ConceFT方法的Rényi熵远小于STFT，且随着信噪比的降低，ConceFT的Rényi熵变化并不大，说明其时频分辨率受信噪比影响不大，说明该方法具有强抗噪性，低信噪比时仍具有高时频分辨率，这是精确提取瞬时转频曲线的前提。

表1 线调频信号不同信噪比下两种方法的Rényi熵

表2 正弦调频信号不同信噪比下两种方法的Rényi熵

为了验证本文方法的瞬时转频估计精度，再取16组不同信噪比的信号进行分析，计算转频估计误差，结果如图12所示，从图12可知,信噪比在-20 dB以上时，估计误差都保持在3%以内，足够满足精度要求。

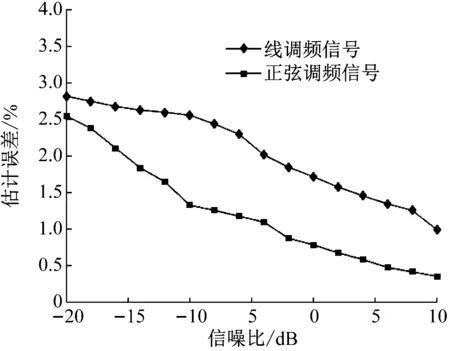
图12 ConceFT对于两种信号转频估计的信噪比-估计误差曲线图

4 实测信号验证

利用实测滚动轴承变转速故障振动信号来进一步验证本文方法的实用性。模拟故障实验台如图13所示。从图13可知，“1”为CA-YD-188型加速度传感器，“2”为ICP激光转速计，试验轴承为外圈有轻微裂纹故障，型号为NU205EM。振动信号采样频率为25 600 Hz，激光转速计采样频率为1 kHz，据此利用五点公式法拟合转频曲线，作为理论转频曲线。本文利用两组数据进行充分验证，分别取转速上升阶段和转速复杂波动变化阶段的轴承故障振动信号。ConceFT算法中选2个标准正交Morse小波，N取为10。

4.1 升速工况下瞬时转频估计精度验证

振动信号波形如图14所示。为强背景噪声干扰下的升速工况，转频由11.4 Hz上升至24.6 Hz。首先对信号进行预处理，低通滤波截止频率设为1 500 Hz，降采样倍数设为5，所得降采样后的采样频率为5 120 Hz，对降采样后的信号去趋势项，再取Hilbert包络，预处理结束。对预处理后的信号进行ConceFT得时频图如图15所示。从图15可知，一倍转频能量最高，最突出，将其作为峰值索搜的目标得转频曲线，经过计算转频估计误差为0.59%，足以满足精度要求。

图13 QPZZ-Ⅱ旋转机械故障试验台

图14 升速工况振动信号波形

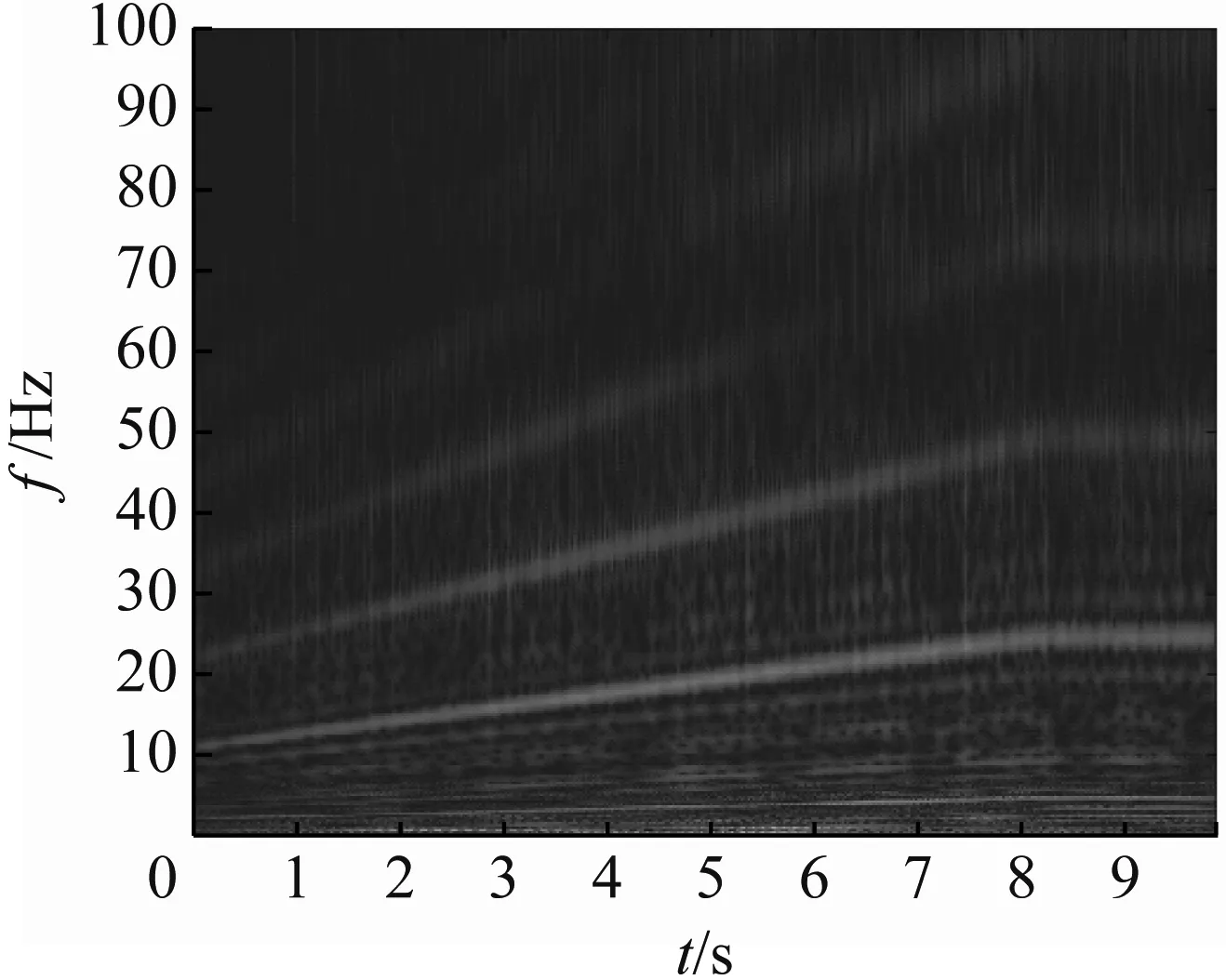
图15 升速工况振动信号ConceFT时频图

4.2 转速剧烈波动工况下瞬时转频估计精度验证

振动信号波形如图17所示。从图17可知，转速升降复杂变化的工况，可见信号中夹杂着大量噪声成分，该信号转频在6～20 Hz之间升降往复变化，转频曲线的提取难度大大增加。首先仍然先对信号进行预处理，同“4.1”所述，对预处理后的信号进行ConceFT得时频图，如图18所示。由图18能清晰识别一倍转频分量，将其作为峰值索搜的目标，得转频曲线如图19中虚线所示。图19中实线为理论转频，可见二者相似度极高，基本重合，经过计算该转频估计误差仅为0.51%。可见，在复杂工况下，该方法仍能保持非常高的估计精度。

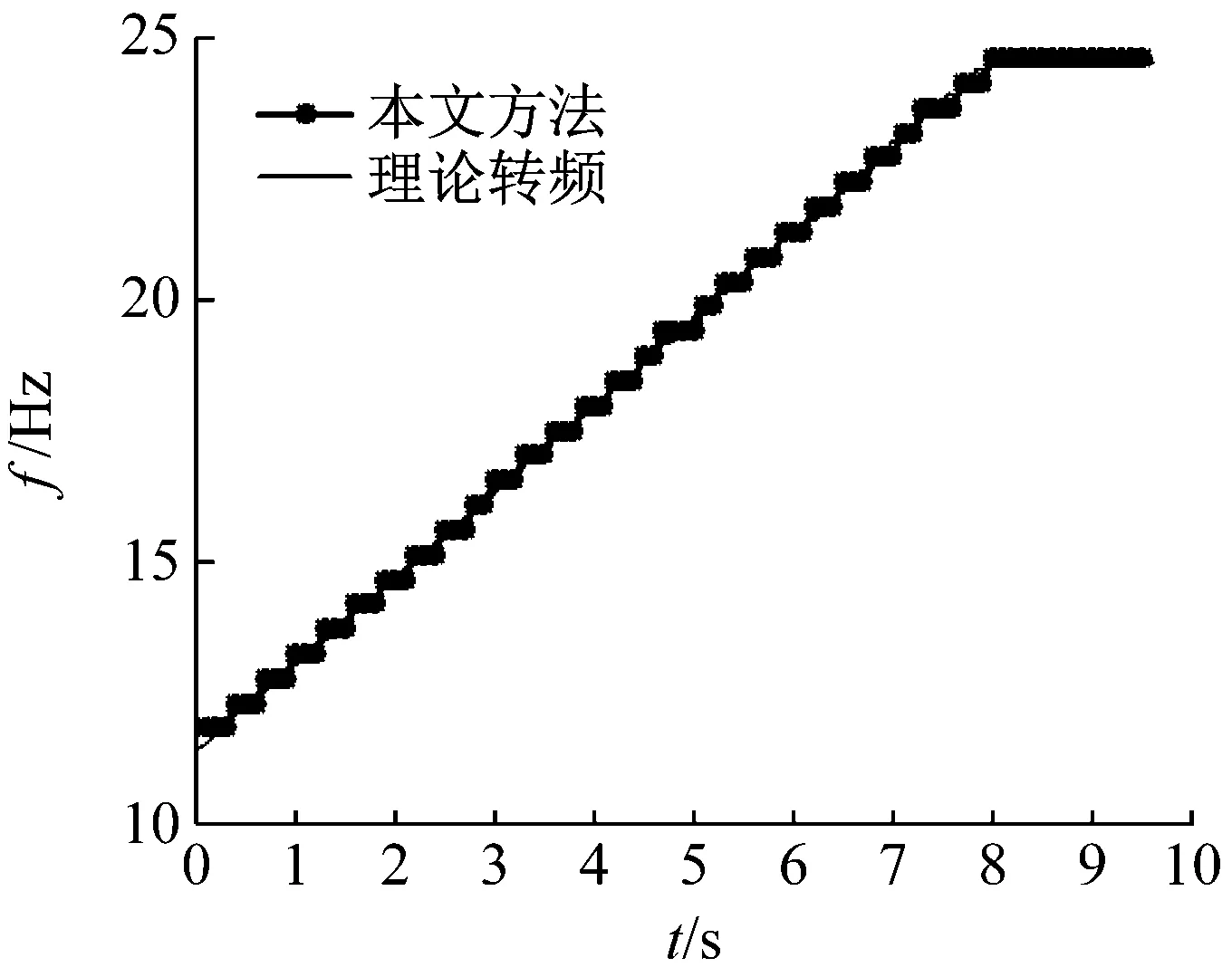
图16 升速工况ConceFT转频曲线估计结果与理论转频对比图

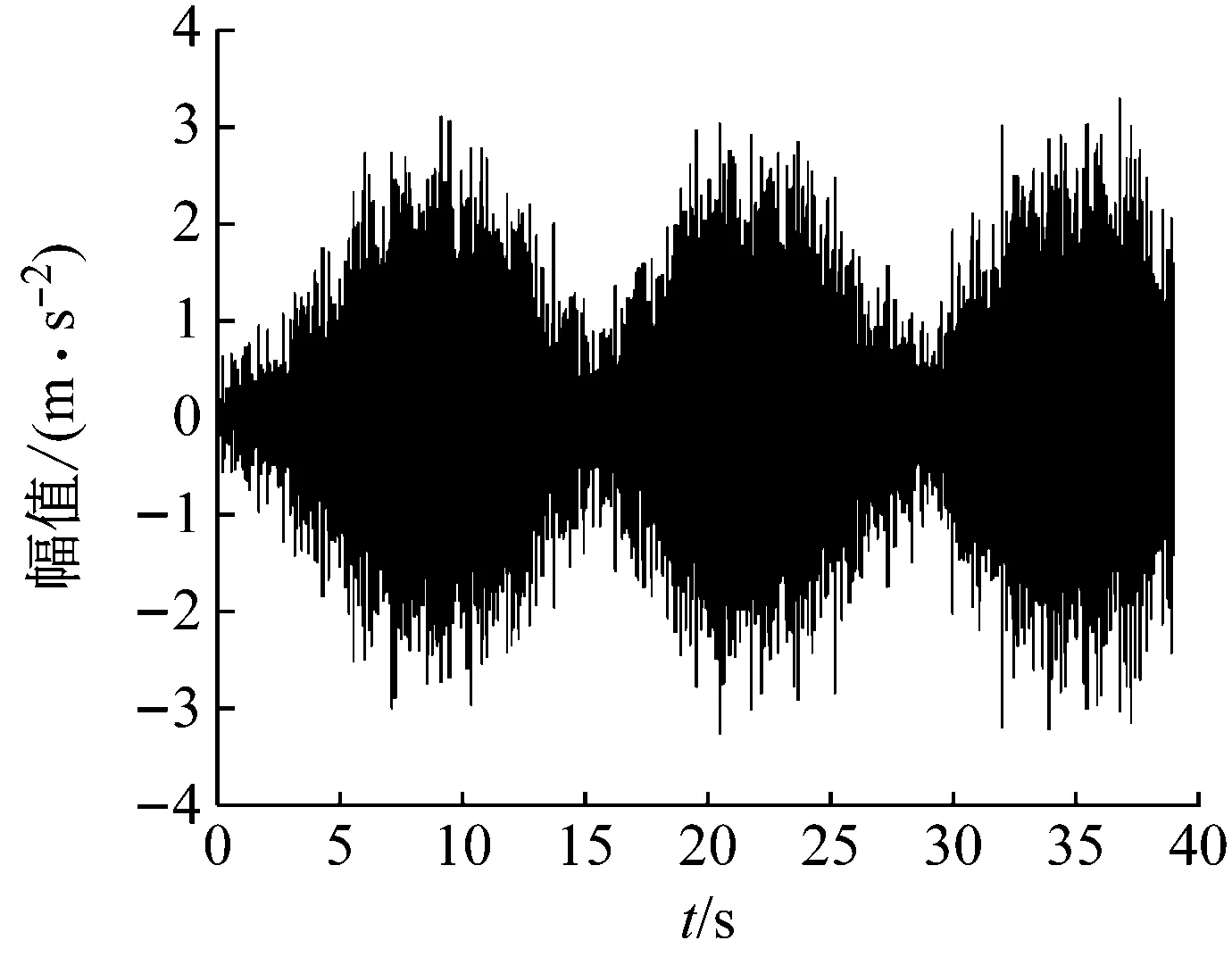
图17 转速波动工况振动信号波形

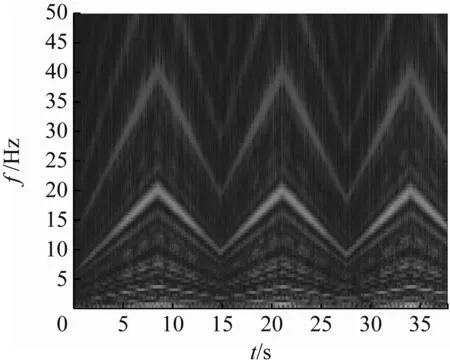
图18 转速波动工况振动信号ConceFT时频图

5 结 论

(1) 分析表明ConceFT方法是一种具有强抗噪性、高分辨率的时频分析方法，将其与峰值索搜结合用于滚动轴承瞬时转频估计，通过仿真信号与两种复杂工况下的变转速故障信号分析，结果验证了该方法在复杂噪声干扰下仍能准确提取信号瞬时转频，准确度高达99%以上，满足高精度的要求，可以用于无转速计情况下的转频估计与转速曲线提取工作，能够解决现有方法抗噪性差及估计精度不足的问题，是一种有实际应用价值的转频估计方法。

图19 转速波动工况ConceFT转频曲线估计结果与理论转频对比图

(2) ConceFT作为一种新兴的时频分析方法，由于其具有强抗噪性及较高的时频分辨率而有广阔的应用空间。如，基于时频分析的变转速轴承故障诊断方法较阶比分析简单直接，但目前的时频分析方法在抗噪性及时频分辨率上通常不能满足要求，利用ConceFT可以很好的解决此问题；齿轮等其他机械设备的故障诊断问题同样可以借助ConceFT来解决；其他领域，如地震信号、油气检测等凡需时频分析的领域均可尝试用ConceFT来处理。