立体交叉隧道结构地震动力响应特性及其相互影响规律振动台试验及数值仿真研究

刘 聪， 彭立敏， 雷明锋,2， 施成华， 李玉峰,3

(1.中南大学 土木工程学院，长沙 410075；2.中南大学 重载铁路工程结构教育部重点实验室，长沙 410075；3.中国建筑第五工程局有限公司，长沙 410004)

在我国大力发展交通基础设施和开发利用地下空间的背景下，不可避免地会出现大量的地下结构立体交叉现象，如东北东部铁路通道在新建过程中，产生了多座立体交叉隧道，仅前阳至庄河段就有7座，交叉隧道的净距最小仅有2.7 m[1]。地下结构向来被认为是一种抗震性能相对优良的结构[2]，但在日本7.2级阪神大地震、台湾7.6级集集地震、2008年8.0级汶川地震等多次地震中，众多山岭隧道及地铁盾构隧道均遭受了不同程度的破坏[3-5]，学者们对强震下隧道结构的震害特性及规律也有了新的认识[6]。

在数值仿真方面，王国波等[7]研究了交叉角度对于立体交叉隧道抗震性能的影响，其结果表明两隧道垂直交叉优于平行重叠。陈磊等[8]探讨了立体交叉隧道的地震响应，结果表明下穿隧道的最大地震加速度大于上跨隧道相应部位，且相邻隧道的存在减小了隧道交叉部位的应力，Chen等[9]对隧道与横通道交叉部位的地震动力特性展开了相关研究，并指出交叉部位由于刚度不连续，结构形式差异显著，导致其抗震性能较为薄弱，在高烈度地震区应加强抗震设计。

在试验研究方面，Tao等[10]针对地铁车站与下穿矩形隧道所成立体交叉结构的地震响应问题，采用单向地震波加载展开振动台试验研究，认为下穿矩形隧道的存在，减小了上部车站的地震响应，而实际地震波是多向的，多向地震波在立体交叉隧道之间将产生更为复杂的反射、衍射现象，其对立体交叉结构的影响有待进一步的试验研究。为研究软土区隧道的地震响应实用计算方法，Moss等[11]通过振动台模型试验和数值仿真研究指出，简化设计算法过高的估计了隧道所受的地震荷载。Hashash等[12]通过振动台试验，对比分析了隧道不同抗震措施的有效性。

Xu等[13]通过振动台三向地震试验研究了隧道的抗震及减振措施的有效性，发现衬砌结构中的钢筋层能够有效阻止隧道在地震中的环向开裂，，而在围岩与衬砌之间设置泡沫减振层可大大减少地震引起的土压力。针对穿越软硬不均、断层地带隧道的地震反应特性，张景等[14]、邹炎等[15]通过试验研究发现断层破碎带及软硬不均地层附近隧道结构的应变产生了显著增大。申玉生等[16]通过振动台试验研究发现，隧道洞口及洞口浅埋段结构为隧道抗震性能的薄弱环节，确定了需要采取加强抗震设计的洞口浅埋段长度。

纵观这些成果，主要针对单一洞室或采用单向加载进行研究，而实际地震波通常是多向加载，且对于立体交叉隧道，地震波在两隧道交叉处将产生复杂的反射、折射现象，使得两立体交叉隧道的地震动力响应不同于普通单体隧道，为此，本文通过模拟真实的三向地震波加载，针对立体交叉隧道在强震作用下的动力响应特性，采用振动台试验及数值模拟展开研究，以期为立体交叉隧道的抗震设计提供参考依据。

1 立体交叉隧道振动台模型试验设计

1.1 相似关系与相似材料

结合既有研究成果，根据重力失真模型和Buckingham定理，在确定几何相似比的基础上推导得到其他相关物理量的相似关系和相似比，如表1所示。

表1 相似系及相似比

确定上述相似关系后，以V级围岩条件为基础，参照标准高速铁路设计规范:TB 10621—2014)[17]选定各物理力学参数，并经配比设计和动三轴样本试验，确定围岩及衬砌相似材料配比，如表2所示。

1.2 试验模型

参照我国(高速铁路设计规范:TB 10621— 2014)，以速度为350 km/h的V级围岩双线隧道复合式衬砌结构断面为原型，如图1所示。并将二次衬砌与初期支护视为一整体结构，得到几何相似比1∶25的缩尺模型，进而设计了交叉隧道模型及模型箱，如图2所示。模型箱尺寸：2 m×2 m×2 m，底板尺寸3 m×3 m。

同时，为减少刚性模型箱边界效应，在模型箱内侧分别衬有厚4 cm厚的聚苯乙烯泡沫板，并在内侧涂抹润滑油。

1.3 传感器布置

为获取隧道环向地震响应规律，在交叉点中心断面(即图3中的1号断面)选取拱顶、拱腰、墙脚、仰拱中心等4个特征点设置传感器测量隧道的地震响应，测试内容包括结构环向应变、水平加速度。

表2 相似材料的物理力学参数及配比

Tab.2 Physico-mechanical parameters and mix proportion of similarity materials

力学参数变形模量/GPa密度/(kg·m-3)内聚力/MPa摩擦角/(°)原型1～21 700～2 0000.12～0.240～50模型0.161 950 0.01540～50配比石英砂∶重晶石∶水泥∶水∶粉煤灰=4.7∶0.85∶0.045∶0.075∶0.25原型31.52 400//模型1.951 650//配比乳化沥青∶水泥∶石英砂∶水=10.85∶11.02∶20.16∶1.52

图1 V级双线隧道复合式衬砌结构

Fig.1 Composite lining structure of tunnel prototype in grade-5 surrounding rock

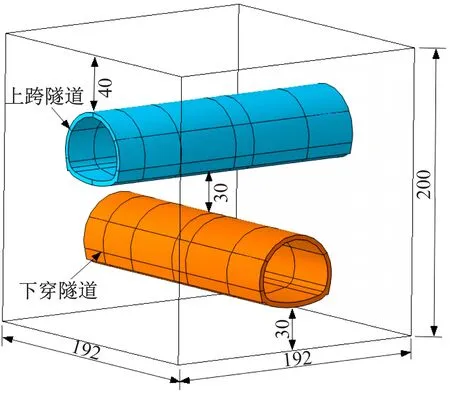
图2 立体交叉隧道空间位置示意图(cm)

Fig.2 Schematic diagram of crossing tunnels’ space position (cm)

为获得立体交叉隧道轴向地震响应特性，在上下两隧道中距离交叉中心不同距离处共设置5个测试断面，在上跨隧道各断面墙脚、下穿隧道各断面拱腰处设置水平加速度计以及轴向应变计，1号断面为交叉中心处断面，2号断面位于交叉区段边缘，2号断面～5号断面与1号断面距离依次为15 cm、45 cm、60 cm、75 cm，根据对称性及衬砌拼接缝特点均匀布置于交叉中心断面两侧，测试断面及特征点,如图3所示。

(a) 上跨隧道(mm)

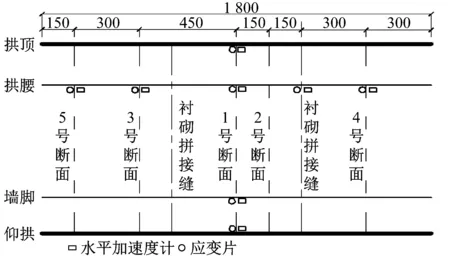
(b) 下穿隧道(mm)

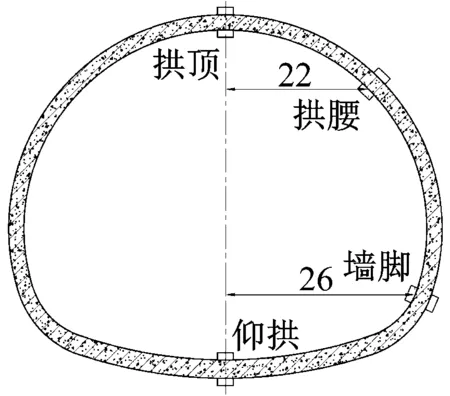
(c) 断面特征点(cm)

传感器布置

1.4 地震激励工况

为满足振动台工作频率，将原始地震波进行0.5～50 Hz带通滤波，相似转换后的El-Centro地震波频率为：0.2～15 Hz；最大加速度0.31g；卓越周期0.46 s，地震持续时间为6.0 s，处理后的加速度时程谱、傅氏谱如图4所示。

本试验考虑Ⅶ度、Ⅷ度和Ⅸ度3种地震烈度影响，并采用3向El波进行加载。其中，研究上跨隧道地震响应规律时，均以主震方向垂直上跨隧道轴线入射获取上跨隧道地震响应数据；而当研究下穿隧道地震响应规律时，均以主震方向垂直下穿隧道轴线加载获取相关试验结果。

参照标准(建筑抗震设计规范:GB 50011—2010)[18]，三向加速度峰值按1(水平1)∶0.85(水平2)∶0.65(竖向)的比例进行加载，设计6种立体交叉隧道地震振动台试验工况，如表3所示。表3中，X向代表垂直上跨隧道轴线的水平方向，Y向代表垂直下穿隧道轴线的水平方向，Z为竖向。

(a) 时程谱

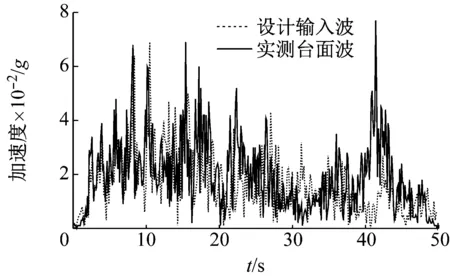
(b) 傅氏谱

表3 试验工况

2 上跨隧道地震响应结果分析

2.1 环向地震响应

2.1.1 加速度

上跨隧道环向上各特征部位的最大地震加速度及其放大系数包络图,如图5所示。从图5可知：① 地震烈度越高，上跨隧道的加速度响应越大，环向特征点最大地震加速度及加速度放大系数按大小排序均为：拱顶>拱腰>仰拱>墙脚，Ⅸ度地震作用下，上跨隧道拱顶处最大地震加速度为1.15g；②上跨隧道加速度受地震烈度影响明显，而加速度放大系数主要受特征点位置控制，不同地震烈度下放大系数变化较小，其中放大系数为隧道最大地震加速度与台面最大加速度的比值。

2.1.2 应变

上跨隧道环向各特征点的最大地震应变,如图6所示。从图6可知:① 地震烈度越高，上跨隧道的应变响应越大，各特征点最大地震应变大小依次为：拱腰>拱顶>墙脚>仰拱;② 不同地震烈度下上跨隧道的最大地震应变均位于拱腰部位，当地震波由Ⅶ度提高至Ⅷ度，最大应变增幅约为60%；Ⅷ度提高至Ⅸ度，最大应变增幅达1.6倍。

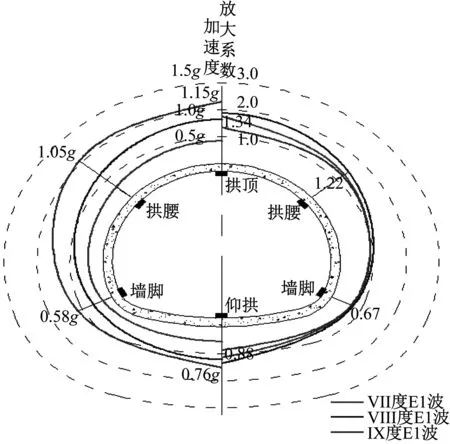
图5 上跨隧道1#断面加速度及放大系数包络图

Fig.5 Envelope diagram of acceleration and magnification factors of cross section 1# in upper tunnel

图6 上跨隧道最大地震应变包络图

Fig.6 Envelope diagram of seismic strain of cross section 1# in upper tunnel

2.2 轴向地震响应规律

2.2.1 加速度

地震波在两隧道立体交叉处产生复杂的反射、折射现象，使得两立体交叉隧道的地震动力响应不同于普通单体隧道，1#断面为交叉中心断面、2#断面位于交叉区域边缘，即位于下穿隧道拱腰竖向垂线对应位置处，1#、2#断面均属于交叉区段范围，5#断面距边界较近，而3#、4#断面与交叉区段及边缘距离均较大，受相邻隧道的干扰小，因此可作为单体隧道断面与交叉区段断面进行对照，上跨隧道加速度轴向分布如图7所示。从图7可知：①上跨隧道地震加速度在交叉中心及端部较小，随与交叉中心的距离增大，上跨隧道墙脚处的最大地震加速度首先逐步增大，距交叉中心60 cm处达到最大值1.03g，随后减小;②在Ⅸ度三向El波作用下，上跨隧道交叉中心处最大地震加速度为0.58g，比距交叉中心45 cm处的普通断面最大加速度减小30.9%。

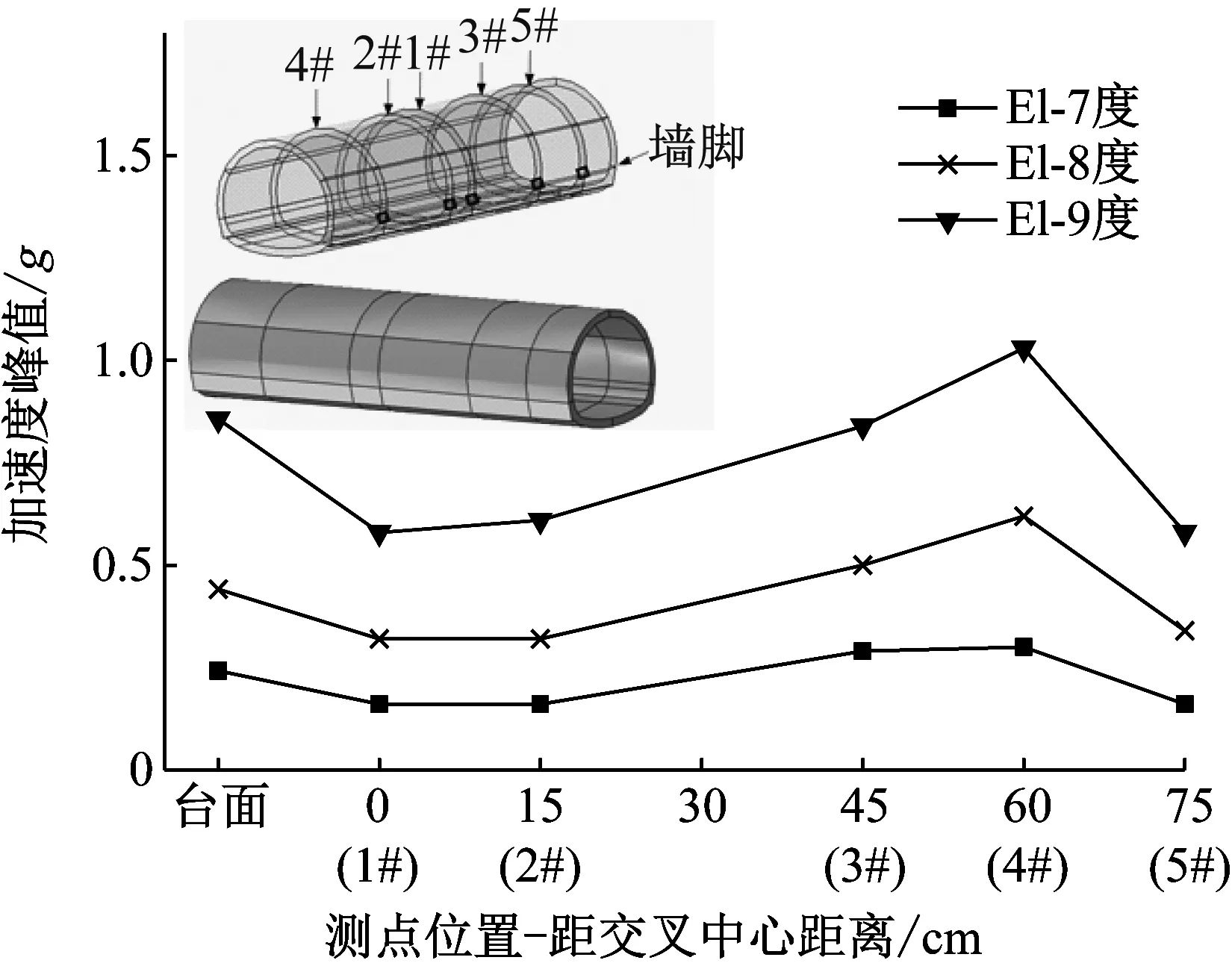
图7 上跨隧道墙脚最大地震加速度及放大系数轴向变化

Fig.7 Axial variations of maximum seismic acceleration in the bottom of upper tunnel’s side-wall

2.2.2 轴向应变

上跨隧道最大地震应变响应沿轴向变化如图8所示。其中2#断面应变计在Ⅸ度地震作用下破坏。从图8可知:① 地震作用下，上跨隧道2#断面地震应变最大，2#和5#断面应变响应峰值明显大于其他3个断面;②Ⅷ度El波加载时，交叉区段隧道最大地震应变为285.6×10-6，比距交叉中心45 cm处普通断面的最大地震应变增大1.7倍。

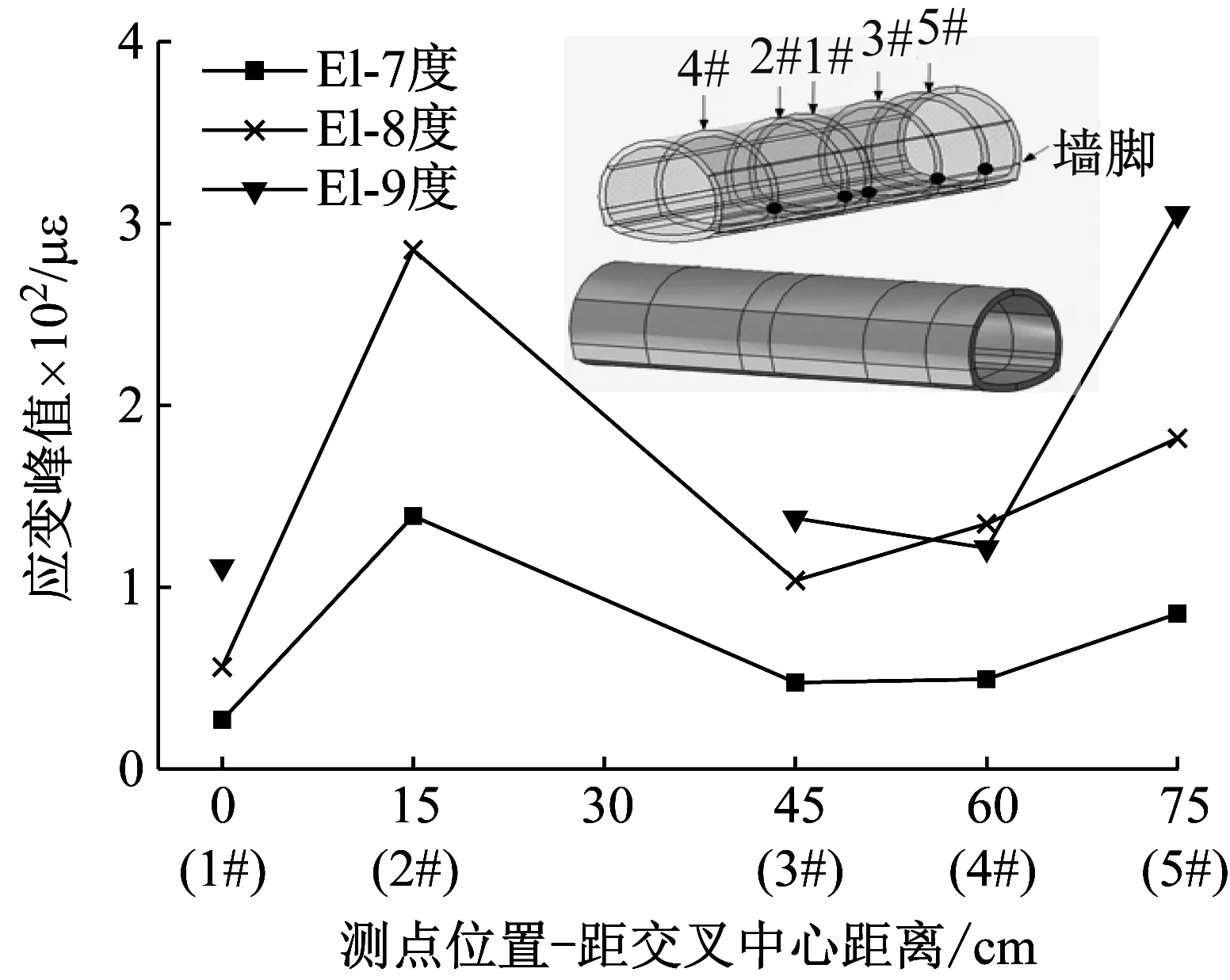
图8 上跨隧道墙脚最大地震应变轴向变化

Fig.8 Axial variations of maximum seismic strain in the bottom of upper tunnel’s side-wall

综合上述分析可见，地震作用下，下穿隧道的存在使上跨隧道的动力响应产生了显著变化：受下穿隧道影响，导致上跨隧道墙脚处最大地震加速度减小，而地震应变则增大。

3 下穿隧道地震响应结果分析

3.1 环向地震响应

3.1.1 加速度

下穿隧道1#断面环向各特征点的最大地震加速度及其放大系数包络图,如图9所示。从图9可知:①下穿隧道1#断面环向各特征点最大地震加速度及加速度放大系数按大小排序均为：拱顶>墙脚>拱腰>仰拱；下穿隧道拱顶、拱腰、仰拱加速度响应均小于上跨隧道，墙脚相反;②下穿隧道最大地震加速度随地震烈度的提高而增大，加速度放大系数随地震烈度变化较小，同时，两立体交叉隧道的最大地震加速度均位于拱顶处，下穿隧道拱顶处最大地震加速度为0.73g。

图9 下穿隧道1#断面加速度及放大系数包络图

Fig.9 Envelope diagram of acceleration and magnification factors of cross section 1# in underpass tunnel

3.1.2 环向应变

下穿隧道环向特征点最大地震应变分布如图10所示。其中拱顶处应变片在Ⅸ度地震烈度工况下破坏，从图10可知:① 下穿隧道环向各特征点按应变大小排序依次为：拱顶>拱腰>墙脚；下穿隧道最大地震应变位于拱顶处，而上跨隧道最大地震应变位于拱腰处;② 与上跨隧道不同，下穿隧道拱顶处地震应变大于上跨隧道，而拱腰、墙脚等部位均小于上跨隧道，其中Ⅷ度El波加载时，下穿隧道拱顶处最大地震应变为149.5×10-6，为上跨隧道拱顶处最大应变的1.6倍。

3.2 轴向地震响应

3.2.1 加速度

下穿隧道拱腰最大地震加速度轴向分布,如图11所示。从图11可知:① Ⅸ度加载时，下穿隧道拱腰最大地震加速度在交叉区段较大，且沿交叉区段边缘往边界其峰值加速度减小，交叉区段内最大地震加速度为0.66g，比距交叉中心45 cm处普通断面大10.0%;② 下穿隧道轴向地震加速度响应规律与上跨隧道相反，地震作用下，由于上跨隧道的存在，使得与之立体交叉的下穿隧道交叉区段的最大地震加速度比普通断面大。

图10 下穿隧道1#断面地震应变包络图

Fig.10 Envelope diagram of seismic strain of cross section 1# in underpass tunnel

图11 下穿隧道拱腰加速度轴向变化规律

Fig.11 Axial variations of acceleration in underpass tunnel’s arch haunch

3.2.2 轴向应变

下穿隧道拱腰处最大地震应变轴向变化规律如图12所示。从图12可知:① 下穿隧道轴向地震应变响应规律与上跨隧道不同，距交叉中心距离越大，环向应变越大，由此可知，上跨隧道的存在，使与之立体交叉的下穿隧道在交叉区段的最大地震应变减小;② 地震作用下，下穿隧道拱腰在交叉区段内(1#、2#)的最大地震应变均小于普通断面(3#、4#断面);③ Ⅸ度El波作用下，下穿隧道交叉区段内最大地震应变为117.2×10-6，比距交叉中心45 cm处的普通断面减小27.2%。

4 数值模拟

4.1 模型

采用ABAQUS建立试验系统的数值模型,如图13所示。模型的尺寸、参数及加载方式均与试验设计一致。

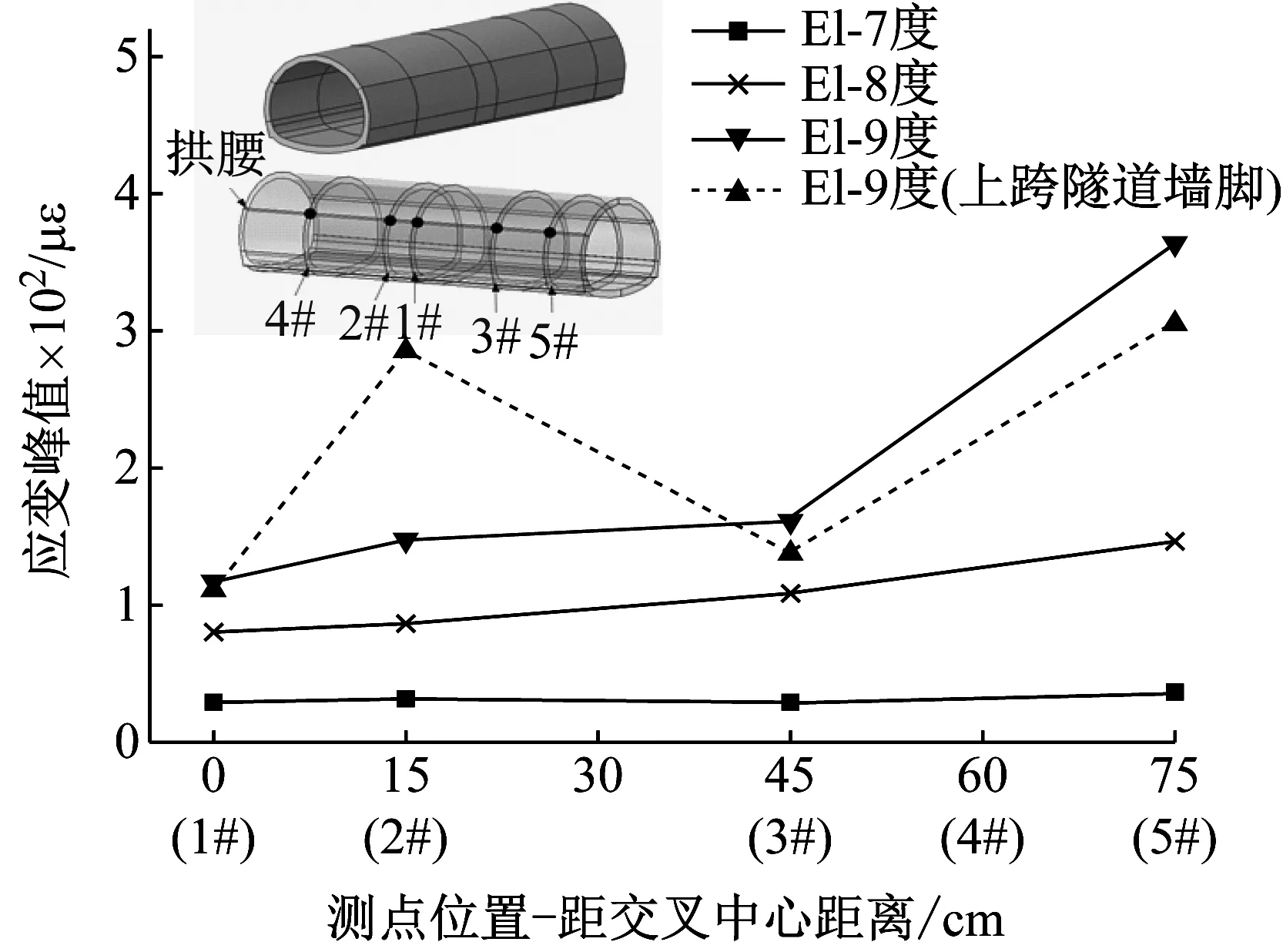
图12 下穿隧道拱腰处应变轴向变化规律

Fig.12 Axial variations of seismic strain in underpass tunnel’s arch haunch

图13 数值模型及网格划分

模型中，围岩采用摩尔-库伦本构模型，混凝土结构采用线弹性模型，围岩及隧道结构相关参数见表2，模型网格共划分为14 096个单元，为消除边界地震波反射影响，数值模型底面及侧面均采用黏弹性边界，边界的法向刚度为83.3 MPa，法向阻尼为9.04×105kg/m2/s，切向刚度为42.0 MPa，切向阻尼为2.29×105kg/m2/s，围岩与隧道之间采用Penalty函数接触关系，摩擦因数为0.33，同时根据模型的自振频率，得围岩材料的瑞利阻尼参数α=1.932 1,β=0.001 3。

4.2 数值模型验证

模型试验结果所得为加速度及轴向应变沿轴向变化，因此在模型底部加载Ⅸ度三向El地震波，由模型计算同样得到两立体交叉隧道相应点位处加速度(X正向)及轴向应变峰值沿轴线变化规律与试验结果进行对比，如图14～图15所示。数值计算及试验得到各特征点加速度及轴向应变峰值数据,如表4所示。

由图14～图15和表4可知:①在边界特征点处，数值计算结果与试验结果存在较大差异，推测这一现象是受试验模型侧向边界产生的反射波干扰所致;②除边界特征点外，数值计算得到的加速度峰值及应变峰值沿隧道轴线方向变化规律与试验结果一致，两者加速度峰值的最大偏差为20.0%，轴向应变最大偏差为13.6%，均位于下穿隧道3#断面处，数值计算与试验所得交叉隧道动力响应特性及相互影响规律是吻合的。

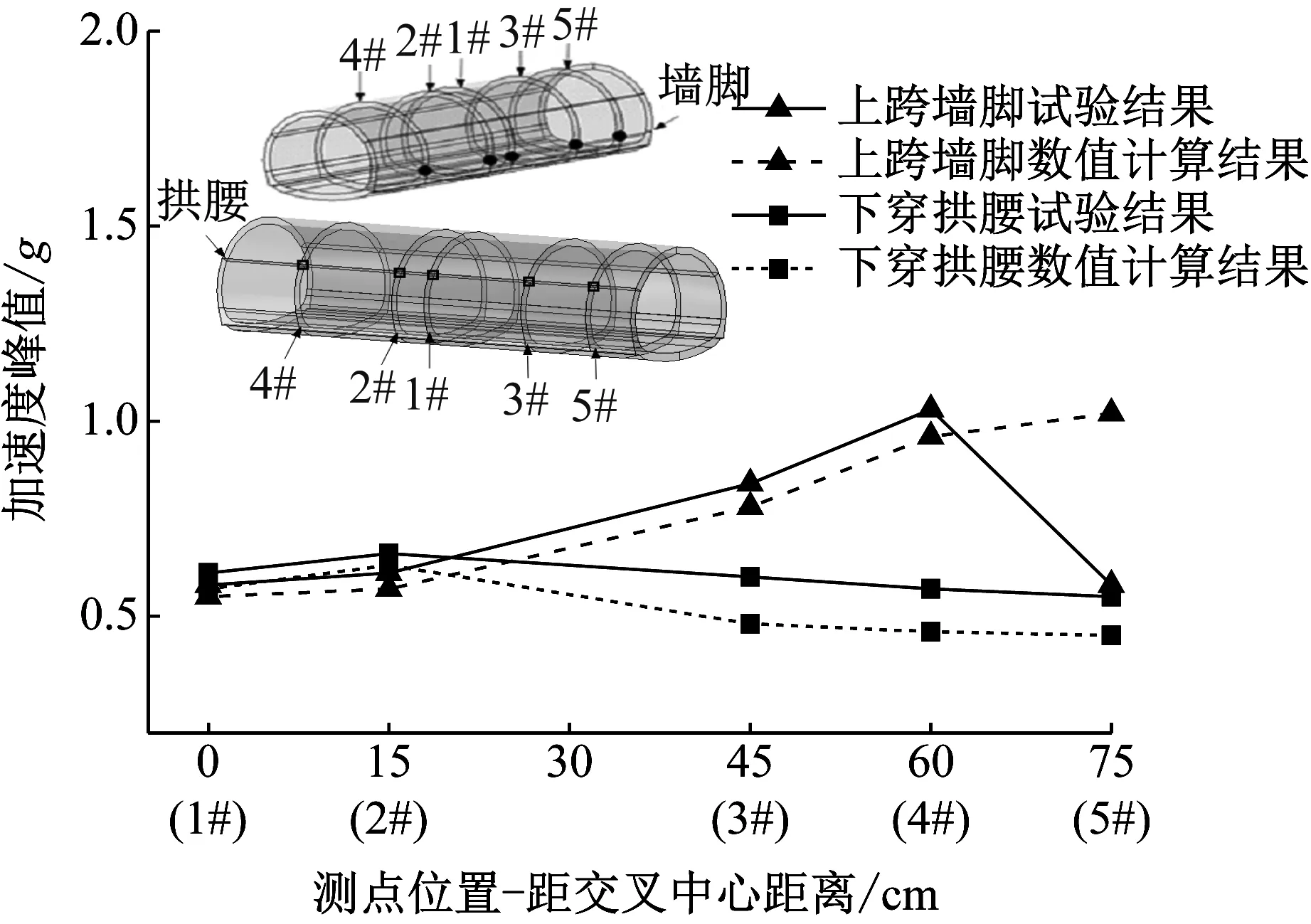
图14 上跨隧道加速度沿轴向变化规律

Fig.14 Axial variations of seismic acceleration of crossing tunnels

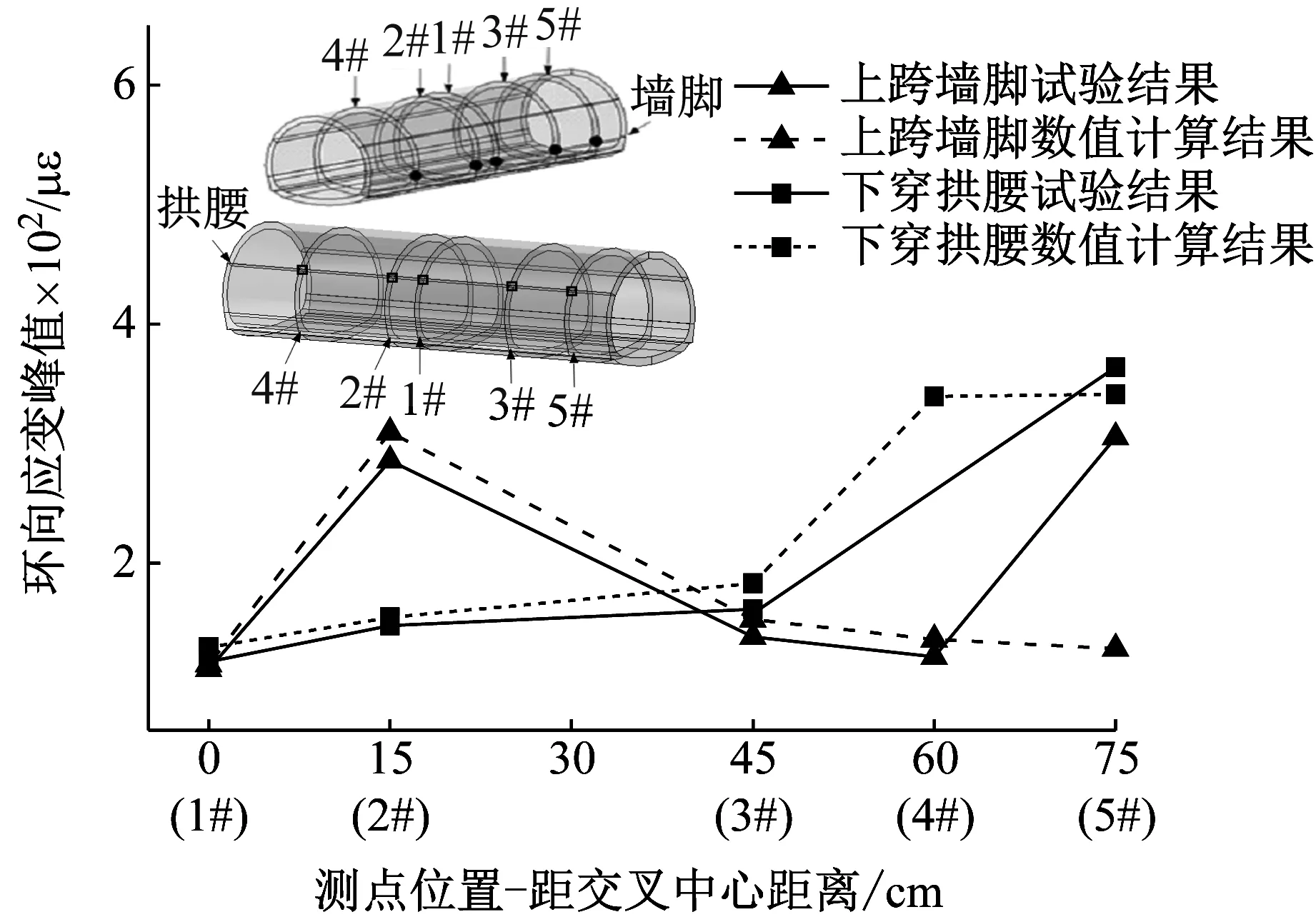
注：图中上跨隧道2#断面应变为Ⅷ度El波下的数据

图15 交叉隧道轴向应变沿轴向变化规律

Fig.15 Axial variations of seismic strain of crossing tunnels

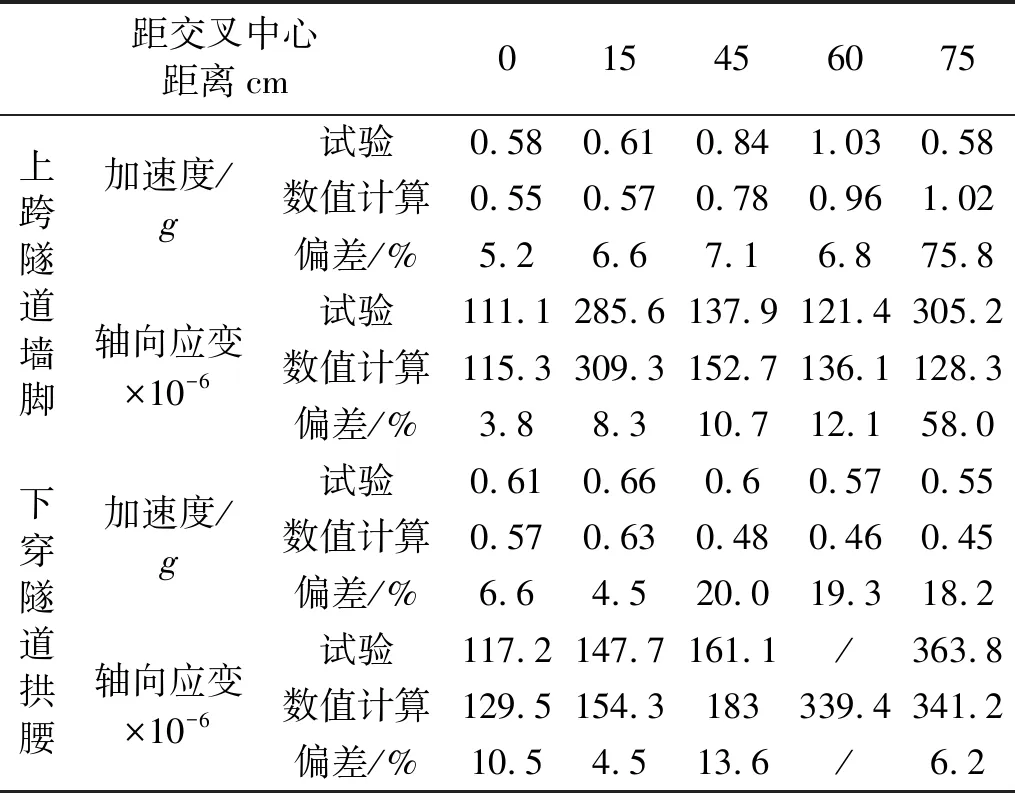
表4 结果对比

4.3 交叉隧道相互影响规律数值计算

在数值模型底部施加Ⅸ度三向El地震波，提取两隧道结构各特征点处的主应力及主震方向位移沿轴向变化情况，以揭示两交叉隧道在地震作用下的相互影响规律。

4.3.1 上跨隧道主应力

Ⅸ度三向El作用下，上跨隧道各特征点主应力峰值沿轴线变化如图16所示。从图16可知:①上跨隧道墙脚处σ1最大，其次为仰拱，在交叉断面处隧道σ1比普通断面处大，交叉中心墙脚处墙脚σ1最大值为2.85 MPa，比3#断面大12.2%;②沿隧道轴线各特征点σ3的绝对值均在交叉中心处最大，交叉中心仰拱处σ3绝对值最大为2.02 MPa，比3#断面大59.1%。

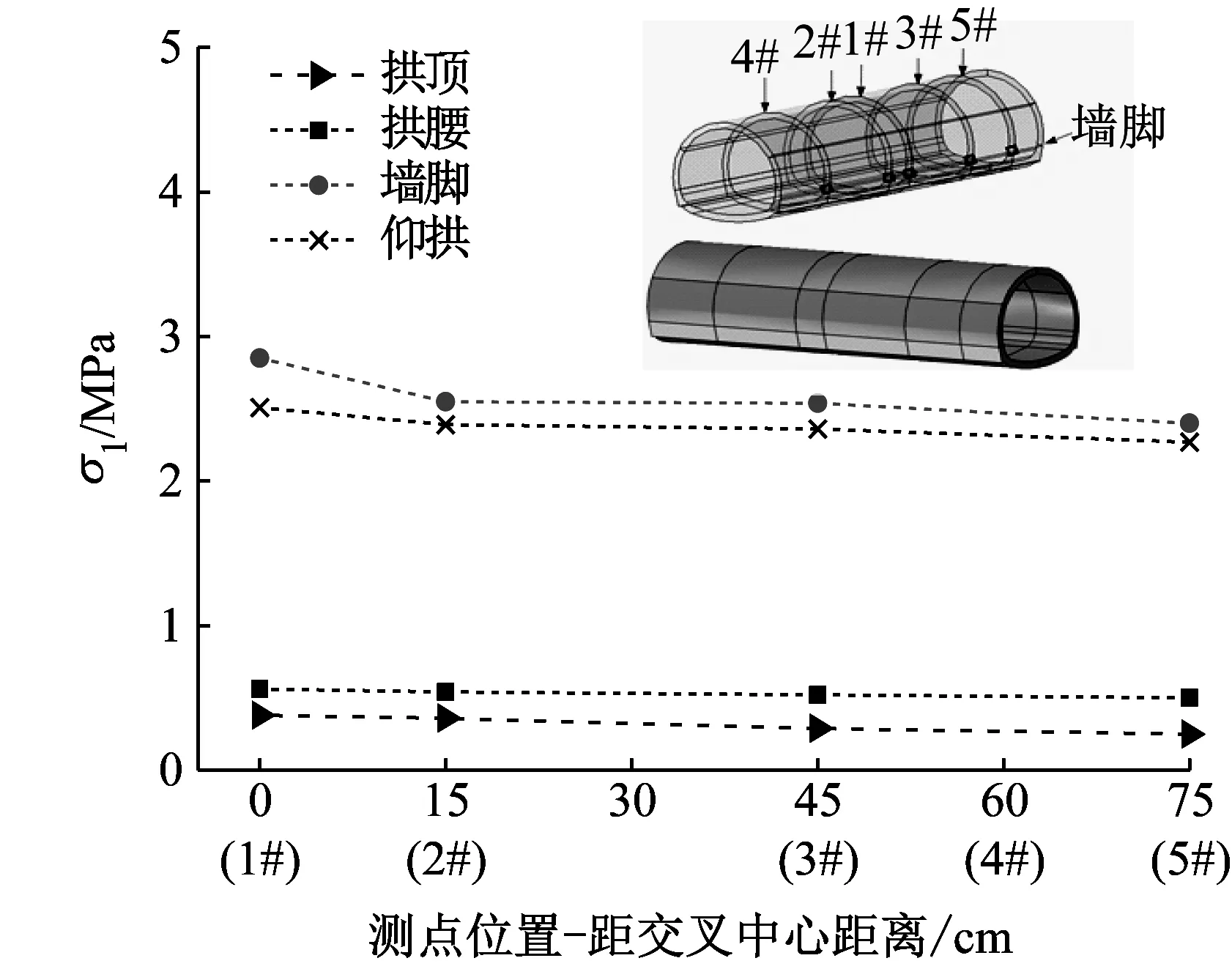
(a) σ1

(b) σ3

4.3.2 上跨隧道主震方向位移

上跨隧道各特征点主震方向位移沿轴向变化,如图17所示。从图17可知：上跨隧道墙脚处隧道沿主震方向位移最大，且各特征点主震方向位移均在交叉中心处最大，交叉中心断面墙脚处沿主震方向的最大位移为2.14 mm，比3#断面墙脚处位移大15.1%。

图17 上跨隧道位移沿轴向变化规律

4.3.3 下穿隧道主应力

下穿隧道各特征点主应力峰值沿轴线变化，如图18所示。从图18可知:①下穿隧道仰拱处σ1最大，在交叉中心断面处隧道σ1比普通断面处小，交叉中心断面仰拱σ1最大值为1.16 MPa，比距交叉中心45 cm的3#小41.7%;②沿下穿隧道轴线各特征点σ3的绝对值均在交叉中心处最小，交叉中心仰拱处σ3绝对值最大为1.09 MPa，比3#断面小41.7%。

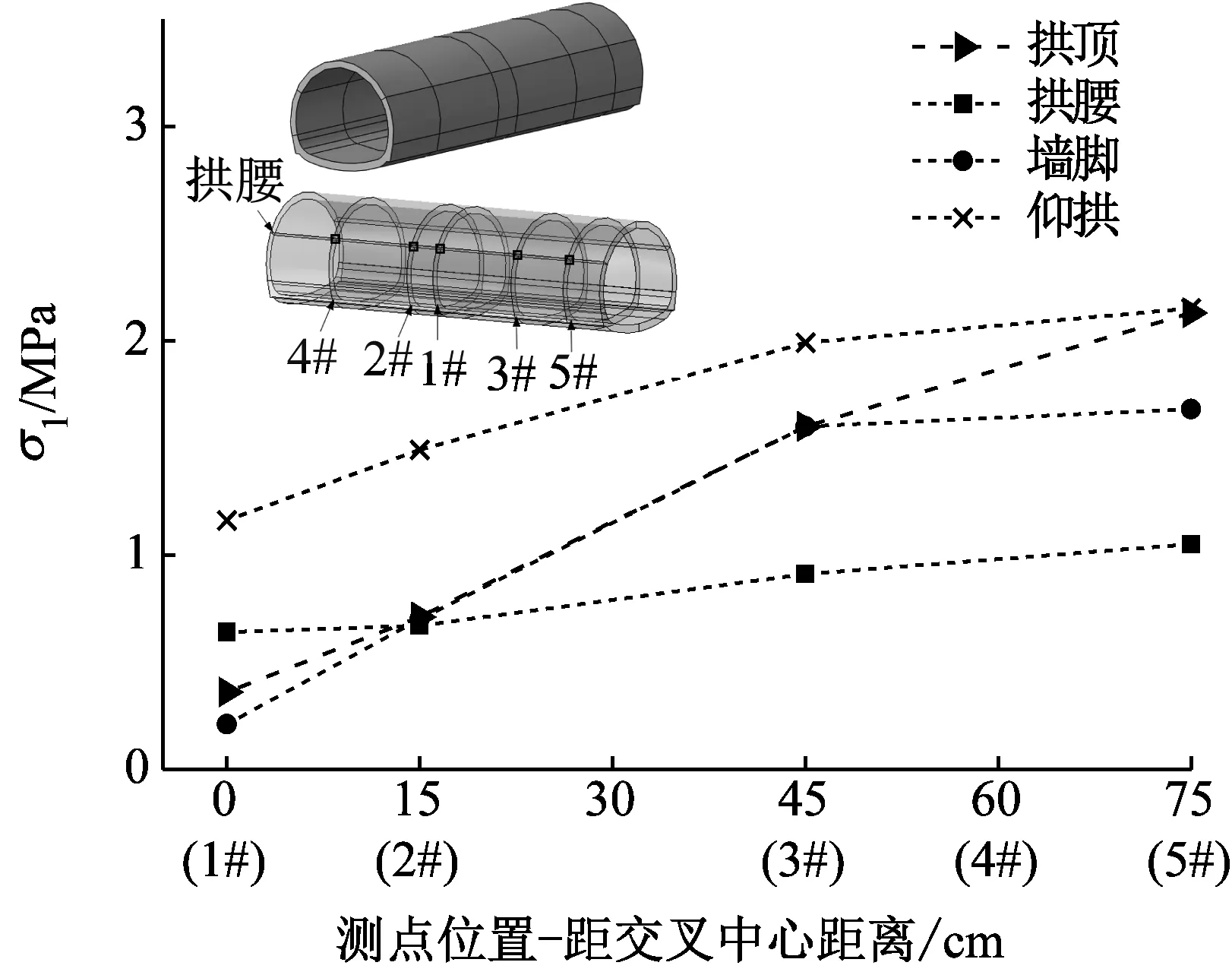
(a) σ1

(b) σ3

4.3.4 下穿隧道主震方向位移

下穿隧道各特征点主震方向位移沿轴向变化,如图19所示。从图19可知：下穿隧道墙脚处隧道沿主震方向位移最大，且各特征点主震方向位移均在交叉中心处最小，交叉中心断面墙脚处沿主震方向的最大位移为11.9 mm，比3#断面墙脚处位移小11.9%。

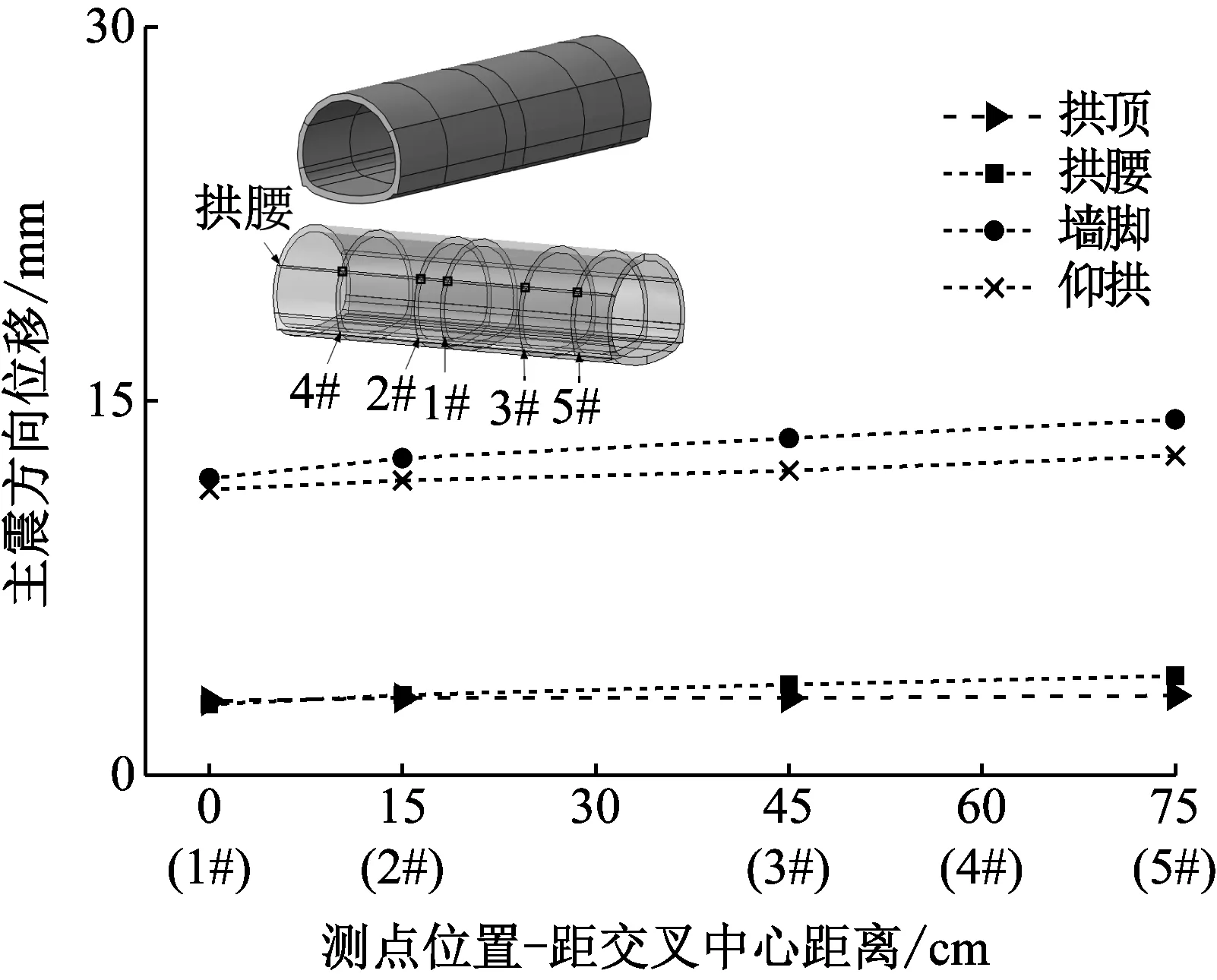
图19 下穿隧道位移轴向变化

5 结 论

针对立体交叉隧道地震响应特性及其相互影响等问题，开展了振动台缩尺试验及数值计算研究，研究结论如下：

(1) 试验结果表明，两立体交叉隧道各特征点的加速度及环向应变峰值均随地震烈度提高而增大。交叉中心断面上跨隧道环向各特征点的加速度及加速度放大系数按大小排序均为：拱顶>拱腰>仰拱>墙脚，环向应变大小排序为：拱腰>拱顶>墙脚>仰拱，在上跨隧道轴向上，交叉中心墙脚处加速度最大值比普通断面(3#)小，而轴向应变比普通断面(3#)大。

(2) 试验结果表明，交叉中心处下穿隧道环向各特征点的加速度峰值及放大系数依次为：拱顶>墙脚>拱腰>仰拱，按环向应变大小排序依次为：拱顶>拱腰>墙脚，在下穿隧道轴线上，交叉中心拱腰处加速度最大值比普通断面(3#)大，而轴向应变比普通断面(3#)小。

(3) 数值计算表明，在Ⅸ度三向El波作用下，受下穿隧道影响，沿轴向上跨隧道，交叉中心断面处各特征点σ1、σ3及主震方向位移最大值分别比普通断面(3#)增大12.2%、59.1%、15.1%。

(4) 数值计算表明，在Ⅸ度三向El波作用下，受上跨隧道影响，沿下穿隧道轴向，交叉中心断面处各特征点σ1、σ3及主震方向位移最大值分别比普通断面(3#)减小41.7%、41.7%、11.9%。