准静态下轮对脱轨安全限值研究

王 健，王 平，马道林，马晓川，徐井芒

(1.中国铁路设计集团有限公司 线站院，天津 300308；2.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031)

自铁路运输诞生以来，列车脱轨事故便一直是威胁铁路运输安全的最主要因素，列车脱轨不仅给社会发展带来严重的损失，还威胁乘客的生命和财产安全。铁路的高速化和重载化发展，使得对列车脱轨问题的研究愈发重要。1896年，法国科学家Nadal根据库伦摩擦定律，推导准静态条件下车轮出现爬轨趋势时接触点的受力平衡条件，并提出著名的Nadal脱轨评判准则[1]，被世界许多国家铁路部门推广，并一直沿用至今。但是，随着世界铁路的快速发展，脱轨事故仍时有发生，车辆脱轨机理至今没有得到充分的解释[2]。

文献[3]采用蠕滑理论重新推导车轮脱轨临界状态下的受力平衡条件，指出Nadal脱轨准则在小冲角下有一定的保守性。文献[4]通过对大量脱轨事故的调查和研究，认为将轮对两侧车轮脱轨系数之和作为评判车轮爬轨的准则更加合理。文献[5]研究摩擦系数和轮轨冲角对车轮爬轨的影响，认为脱轨系数超限距离对车轮爬轨有重要的影响，而脱轨系数超限持续时间则对车轮爬轨影响不大。文献[6-7]通过建立准静态下车轮脱轨的三维模型，较全面地考虑了轮轨间的蠕滑作用及轮轨冲角对车轮脱轨的影响。国内，文献[8]在单轮对试验台上模拟轮对脱轨的过程，认为轮轨冲角和轮重减载对车轮脱轨有较大影响。文献[9]通过轮对脱轨试验研究车轮的脱轨过程以及脱轨过程中轮轨接触状况和车轮悬浮量的变化。文献[10]通过等效摩擦系数替代摩擦系数的方式对Nadal脱轨系数进行改进，并给出等效摩擦系数的计算方法。文献[11]在Nadal准则的基础上，研究轮重减载对轮对脱轨的影响。文献[12-13]分析脱轨过程中轮对的三维受力平衡条件，提出同时考虑轮轴脱轨系数和轮重减载率的脱轨评判准则。此外，文献[14-15]将车辆能量随机分析理论应用于脱轨分析中，给脱轨问题的研究带来了新的思路。文献[16-17]基于车辆-轨道耦合动力学理论，提出将车轮抬升量作为车轮脱轨的评价标准。

本文基于准静态下三维轮对脱轨分析模型，推导轮对脱轨临界状态下的力学平衡方程，建立轮对稳态脱轨的评价方法。采用非线性蠕滑理论充分考虑轮轨蠕滑力及摩擦系数对轮对脱轨安全限值的影响，并与文献[13]计算结果进行对比。

1 准静态下轮对脱轨分析模型

1.1 轮轨系统坐标系

轮轨接触关系是耦合车轮与钢轨的纽带，而建立轮轨系统坐标系是确定轮轨关系的基础。如图1所示，建立轨道坐标系(OtXtYtZt)、轮对坐标系(OwXwYwZw)及轮轨接触点坐标系(OlXlYlZl和OrXrYrZr)。轨道坐标系固结于轨道中心线，并以一定速度v沿轨道中心线移动；轮对坐标系固结于轮对质心位置，随轮对一起运动，其相对轨道坐标系有平移及转动自由度；接触点坐标系固结于轮轨接触斑中心位置，并随轮对一起运动。

根据图1，轮对坐标系至轨道坐标系间的变换关系为

(1)

式中：ψ为轮对摇头角；φ为轮对侧滚角。

左右两侧轮轨接触斑坐标系至轮对坐标系间的变换关系为

(2)

式中：δl，r为轮对左右侧车轮的接触角。

将式(2)代入式(1)，接触点坐标系与轨道坐标系间的变换关系为

(3)

式中：Al，r为坐标系转换矩阵

考虑到ψ、φ较小，则Al，r可以化简为

(4)

1.2 准静态条件下轮对脱轨安全限值

轮对稳态脱轨的临界状态下，左右两侧轮轨接触斑受力如图2所示，其中左轮为踏面接触，右轮为轮缘接触。图2中，Fl、Fr、Ql、Qr、Pl、Pr分别为轨道坐标系下两侧车轮作用于接触斑的纵向力、横向力及垂向力；Txl、Txr、Tyl、Tyr、Nl、Nr分别为接触斑坐标系下两侧钢轨作用于接触斑的纵向蠕滑力、横向蠕滑力及法向力。

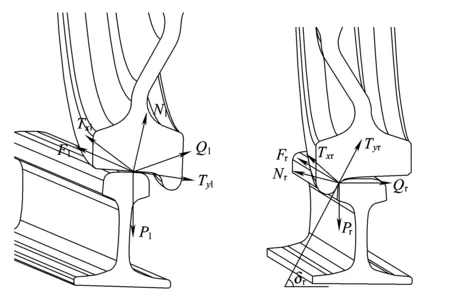
(a)左轮轨 (b)右轮轨

准静态条件下，根据接触斑坐标系与轨道坐标系的关系以及轮轨接触斑受力平衡条件，有

(5)

将式(4)代入式(5)，可以得到左右两侧车轮的脱轨系数(横向力与垂向力的比值)

(6)

(7)

由于轮对侧滚角φ较小，若忽略φ则式(6)、式(7)可以进一步简化为

(8)

(9)

当δr为最大轮缘接触角时，式(9)即为准静态条件下车轮三维脱轨系数临界值的计算式，其在Nadal公式的基础上考虑了轮对摇头及切向力的影响，避免了轮轨间小冲角及负冲角时Nadal公式过于保守的影响。然而，脱轨系数虽然是评价车辆脱轨安全性的最基本指标，但仅依靠脱轨系数来判定安全性却并不充分。一方面，当垂向力较小时，使用该垂向力与对应横向力计算得到的脱轨系数很容易达到脱轨限界值；另一方面，在脱轨系数的实际测量中，当轮重减载较大时与其对应的横向力一般也较小，计算脱轨系数时轮轨垂向力和横向力测量误差的影响较大，难以得到较准确的脱轨系数。文献[18]指出，根据多次线路试验，轮重减少得越多越容易导致列车脱轨。因此，一些国家除采用脱轨系数外，还提出了将轮重减载率作为车辆脱轨的评价标准。

根据轮重减载率的定义，假设轮缘接触侧车轮轮重为减载，则轮对两侧车轮轮载与轮重减载率间的关系为

(10)

式中：P0为车轮静轮重，即为静轴重的一半；ΔP为车轮轮重变化量；ΔP/P0为轮重减载率。

准静态条件下，为保证车轮不脱轨，轮对横向受力需满足

H≤Qr-Ql

(11)

式中：H为轮轴横向力。将式(8)～式(10)代入式(11)，可以得到

(12)

定义H/P0为轮轴脱轨系数，其为轮轴横向力与车轮静轮重的比值或轮轴横向力与轮对静轴重比值的2倍，由于轮对静轴重为定值，其实质是规定了轮对在脱轨临界状态下，保证轮对不发生爬轨脱轨和滑轨脱轨所需要的最大轮轴横向力的限值。脱轨临界状态下的轮轨接触参数已知时，便可以求得轮对两侧车轮的脱轨系数，通过式(12)可建立采用轮轴脱轨系数及轮重减载率双重指标对轮对脱轨安全性进行评价的统一公式。同时，当轮轴脱轨系数和轮重减载率满足式(12)时，称为轮对脱轨的安全域，如图3所示。

图3 轮对脱轨安全限值与脱轨安全域

目前，传统的脱轨评价指标主要有三种：脱轨系数、轮重减载率及轮轴横向力。轮重减载率和脱轨系数主要是用来评价车辆爬轨脱轨和滑轨脱轨的安全性，而传统轮轴横向力则主要是评价轨道结构的横向稳定性及是否会发生轨排横移或钢轨倾覆，这与本文所论述的最大轮轴横向力限值的含义有所不同。本文假定轨道结构承载能力能够满足要求，主要考察轮轴横向力是否会引起车轮爬轨脱轨或滑轨脱轨的发生，当需要考虑轨道结构的横向稳定性及承载能力时，需比较本文所述的最大轮轴横向力限值和满足轨道结构横向稳定性及承载能力的轮轴横向力限值，取二者较小值作为安全性评价标准。

2 轮轨蠕滑模型

轮轨蠕滑模型包括轮轨蠕滑率和蠕滑力计算两部分，其直接影响车轮脱轨系数的计算结果，对轮对脱轨安全域的求解至关重要。

2.1 轮轨蠕滑率

准静态条件下，忽略轮轨运动速度及加速度，轮轨蠕滑率可通过式(13)计算[19]。

(13)

式中：ξx(l，r)、ξy(l，r)、ξs(l，r)分别为左右侧轮轨接触斑内的纵向蠕滑率、横向蠕滑率及自旋蠕滑率；rl，r为左右侧轮轨接触点处实际滚动圆半径；r0为车轮的名义滚动圆半径。由式(13)可知，准静态条件下的蠕滑率只与轮轨接触几何参数有关。

2.2 轮轨蠕滑力

得到车轮脱轨临界状态下的蠕滑率后，便可计算轮轨接触斑内的蠕滑力。文献[13]认为在轮对脱轨临界状态下，轮对两侧轮轨接触斑为全滑动状态，同时忽略自旋蠕滑率对横向蠕滑力的影响，根据库伦摩擦定律得到纵向蠕滑力和横向蠕滑力的计算式。

(14)

将式(14)代入式(12)便可确定轮对脱轨安全限值与脱轨安全域的计算公式

(15)

文献[20]指出在轮缘接触时自旋蠕滑率对横向蠕滑力有明显影响，其值可达到横向蠕滑率的70%，在车轮脱轨分析中不可忽略。因此，本文根据Kalker线性蠕滑理论[21]建立可考虑自旋蠕滑率影响的蠕滑力计算模型，根据Shen-Hedrick-Elkins非线性蠕滑模型[20]对蠕滑力进行修正，使蠕滑力饱和后满足库伦摩擦定律。

根据Kalker线性蠕滑理论，蠕滑力与蠕滑率存在如下关系

(16)

Kalker线性蠕滑力模型假设接触斑内无相对滑动，没有考虑接触斑在大蠕滑甚至全滑动状态下需满足库伦摩擦定律的条件，仅在小蠕滑情况下适用。沈志云等在其基础上采用式(17)对线型蠕滑力进行了修正，即

(17)

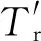
(18)

Tr=

(19)

由上述分析可知，当轮轨接触参数已知时，蠕滑力大小只与法向力有关，想求得蠕滑力需先计算轮轨法向力。由式(5)中接触点垂向受力平衡可以得到

Ty(l，r)Nl，r(φcosδl，r±sinδl，r)-

Nl，r(cosδl，r∓φsinδl，r)+Pl，r=0

(20)

忽略侧滚角后，可以得到

±Ty(l，r)Nl，rsinδl，r-Nl，rcosδl，r+Pl，r=0

(21)

给定轮轨垂向力P时，可通过式(21)迭代求解得到轮轨法向力，进而得到蠕滑力。

3 算例分析

为对比文献[13]计算方法与本文计算方法的差异，以我国某型动车组所采用的LMA车轮踏面和60 kg/m标准钢轨廓形为例，分别计算轮对脱轨的安全限值，具体计算参数见表1。

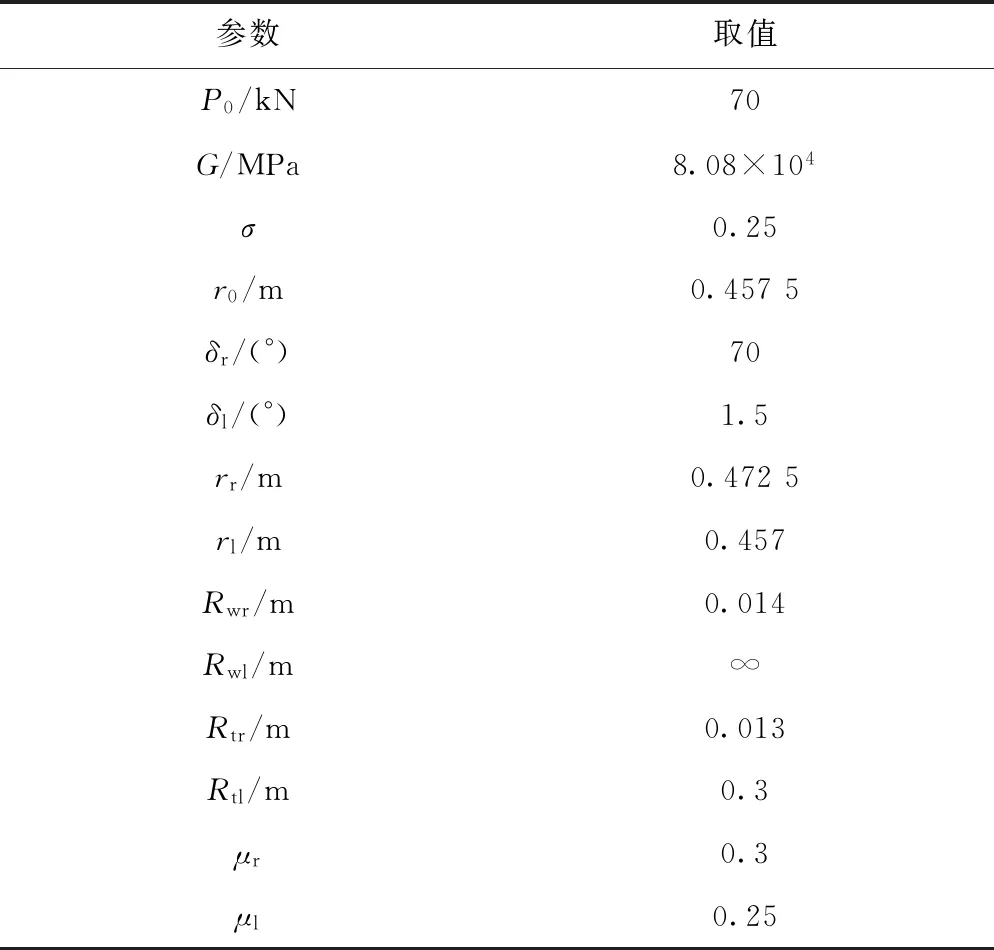
表1 轮轨接触参数

注：σ为泊松比；Rwl、Rwr为车轮接触点处型面的曲率半径；Rtl、Rtr为钢轨接触点处型面的曲率半径。

图4给出了脱轨临界状态下文献[13]与本文计算横向蠕滑力的对比。由图4(a)可知，在踏面接触侧，文献[13]与本文计算结果基本重合，说明自旋蠕滑率对横向蠕滑力的影响较小，这主要是由于踏面接触时接触点处的接触角较小。由图4(b)可知，在轮缘接触侧，轮对正摇头角较小时本文所计算得到的横向蠕滑力比文献[13]结果大，而在负摇头下，本文计算得到的横向蠕滑力比文献[13]结果小。此外根据图4(b)中在轮缘接触侧两种方法计算的横向蠕滑力比值来看，在摇头角为-0.5°～0.5°范围内，二者比值最大可达到5，最小时趋于0，进一步说明在轮缘接触侧的蠕滑力计算中不能忽略自旋蠕滑率的影响。

(a)踏面接触侧

(b)轮缘接触侧

由图4(b)还可以看出，轮缘接触侧横向蠕滑力的方向与轮对摇头角有关。如图5所示，当轮对摇头角为正时(轮轨间冲角为正)，轮缘接触点有一定的超前，造成接触点的速度与车轮脱轨方向相反，则横向蠕滑力与车轮脱轨方向相同(为正值)，对车轮脱轨有促进作用，这种脱轨方式称为爬轨脱轨。如图6所示，当轮对摇头角为负时(轮轨间冲角为负)，轮缘接触点有一定的滞后，造成接触点的速度与车轮脱轨方向相同，则横向蠕滑力与车轮脱轨方向相反(为负值)，对车轮脱轨有阻碍作用，这种脱轨方式称为滑轨脱轨。

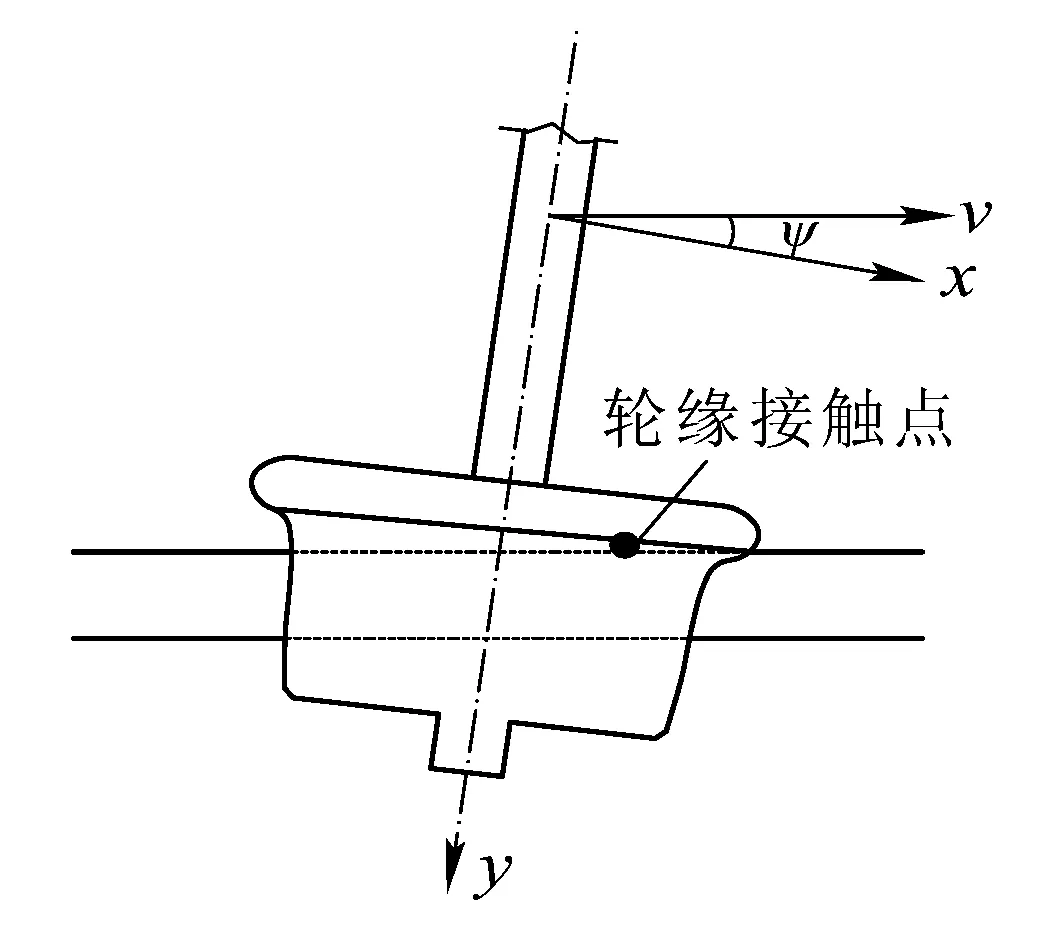
(a)俯视图

(b)车轮侧视图

(a)俯视图

(b)车轮侧视图

将文献[13]与本文计算的轮轨蠕滑力和法向力代入式(8)和式(9)，可以得到轮对脱轨临界状态下两侧车轮的脱轨系数，如图7所示。

由图7可知，两种蠕滑力计算方法计算得到的两侧脱轨系数变化规律基本一致。由于轮缘接触侧车轮的接触角较大，文献[13]在蠕滑力计算中忽略了自旋蠕滑率对横向蠕滑力的影响，造成采用文献[13]计算得到的脱轨系数较本文计算结果偏大，尤其是在正摇头角较小和负摇头角情况下，两者差异较明显。从踏面接触侧车轮的脱轨系数来看，两种方法计算结果基本相同。

(a)轮缘接触侧车轮(右轮)脱轨系数

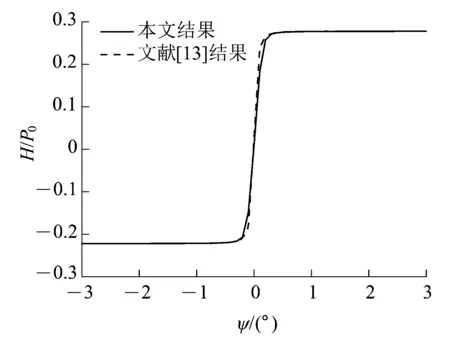
(b)踏面接触侧车轮(左轮)脱轨系数

将图7中轮对不同摇头角情况下两侧车轮的脱轨系数计算结果代入式(12)，可以得到轮对脱轨安全限值及脱轨安全域，如图8所示。

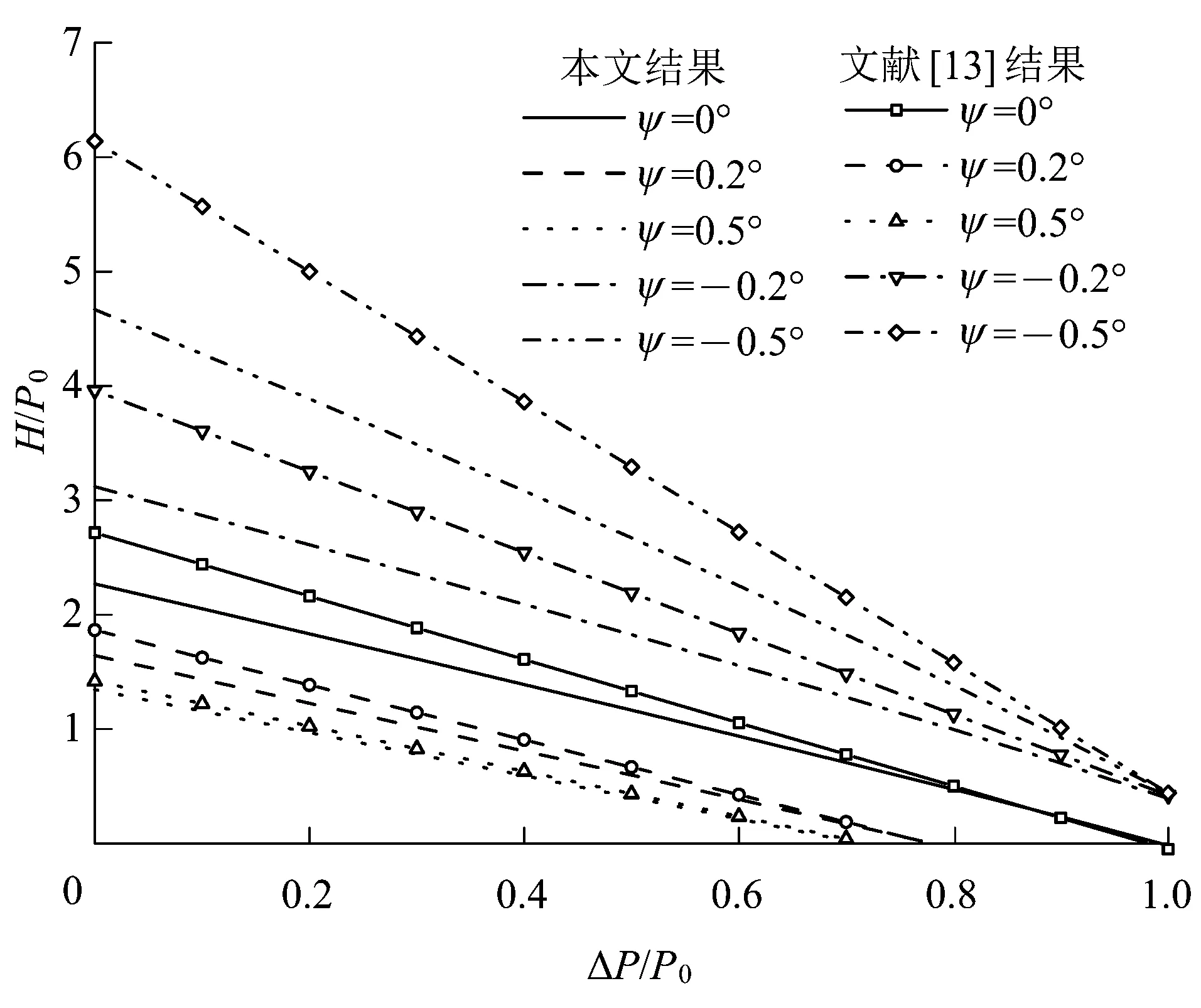
图8 不同摇头角下轮对脱轨安全限值与脱轨安全域

由图8可知，轮对摇头角相同条件下，本文计算得到的轮对脱轨安全域比采用文献[13]方法计算得到的轮对脱轨安全域小。这主要表现在两个方面，一方面是本文计算得到的轮对脱轨安全限值线的斜率绝对值小于文献[13]结果；另一方面，当轮重减载率为0时，本文计算得到的轮轴脱轨系数限值也小于文献[13]结果。此外，二者之间的差异与轮对摇头角密切相关，当轮对摇头角为正时，二者之间的差异随着摇头角的增加而减小；当轮对摇头角为负时，二者之间的差异随着摇头角的增加而增大。

由图8还可以看出，随着轮重减载率的增加，轮轴脱轨系数限值随之减小，说明轮重减载大更容易引起车辆脱轨。此外，轮对的脱轨安全域还与轮对摇头角有密切关系，当摇头角为正时，摇头角越大，轮对脱轨安全域越小，越容易发生脱轨；而摇头角为负时，摇头角越大，轮对脱轨安全域越大，脱轨风险越小。这主要是由于正摇头角下，右侧车轮为爬轨脱轨，横向蠕滑力有帮助车轮脱轨的作用；而负摇头角下，右侧车轮为滑轨脱轨，横向蠕滑力对车轮脱轨有阻碍作用。

通过上述分析可知，由于文献[13]在蠕滑力计算中忽略了自旋蠕滑率的影响，相同轮重减载率情况下，其计算得到的轮轴脱轨系数限值偏大，若以此作为脱轨安全性评价标准则较为宽松，可能会对车辆脱轨的评价产生不利影响。

轮轨间摩擦系数对轮对脱轨安全限值及脱轨安全域的影响如图9、图10所示。从图9、图10可以看出，当轮对摇头角为正时(爬轨脱轨)，降低两侧轮轨间的摩擦系数，均可以增大轮对脱轨安全限值及脱轨安全域，对行车安全性有利；当轮对摇头角为负时(滑轨脱轨)，降低两侧轮轨间的摩擦系数尤其是轮缘接触侧摩擦系数，反而会减小轮对脱轨安全限值和脱轨安全域。

(a)踏面接触侧

(b)轮缘接触侧

(a)踏面接触侧

(b)轮缘接触侧

图11为摩擦系数为0.1时轮对摇头角取0.5°和-0.5°的对比结果。虽然在相同轮重减载率下ψ=-0.5°时要明显大于ψ=0.5°时的轮对脱轨安全域限值，但是车轮爬轨脱轨和滑轨脱轨属于不同的脱轨机制，本文不建议在相同轮重减载率下比较。ψ=-0.5°、轮重减载率为0.5的情况下，其轮轴脱轨系数便达到了ψ=0.5°、轮重减载率为0的轮轴脱轨系数限值；当ψ=-0.5°、轮重减载率在0.5～1.0范围时，轮轴脱轨系数限值便与摇头角为0.5°、轮重减载率在0～0.6情况下的幅值相当，轮对亦会有发生爬轨脱轨的可能。因此，降低轮轨间的摩擦系数对车辆脱轨安全性有利有弊，轮轨间过低的摩擦系数也可能引发车辆脱轨，在确定合理的轮轨摩擦系数时应注意权衡车轮爬轨脱轨与滑轨脱轨。

图11 μ=0.1时轮轴脱轨系数限值对比

4 结论

(1)本文通过建立准静态条件下车轮脱轨临界状态的力学模型，将脱轨系数与轮重减载率耦合在一起，提出了将轮轴脱轨系数和轮重减载率共同作为轮对脱轨安全性评价的统一指标，简化了车辆脱轨的评价方法。同时，该指标引入了轮对摇头角对车辆脱轨的影响，可以避免Nadal脱轨准则在小冲角及负冲角情况下太过保守的影响。

(2)本文采用非线性蠕滑理论充分考虑了轮轨蠕滑力及摩擦系数对轮对脱轨安全限值的影响，并与文献[13]计算结果进行了对比，结果表明自旋蠕滑率对轮对脱轨安全限值与安全域影响明显；忽略自旋蠕滑率，将使计算得到的轮对脱轨安全限值偏大，若以此作为脱轨安全性评价标准则较为宽松，可能会对车辆脱轨的评价产生不利影响。

(3)降低轮轨间的摩擦系数对车辆脱轨安全性有利有弊，轮轨间过低的摩擦系数也可能引发车辆脱轨，在确定合理的轮轨摩擦系数时应注意权衡车轮爬轨脱轨与滑轨脱轨。

(4)在实际应用中，本文提出的车辆脱轨评价方法除利用传统脱轨评价指标中的轮重减载率及轮轴横向力测试结果外，还需对轮对摇头角进行测试，因此需对轮对摇头角的在线测试技术开展进一步研究。

(5)本文以轨道结构承载能力能够满足要求的假设为基础，主要关注车轮的爬轨脱轨和滑轨脱轨，未考虑轮轴横向力作用对轨排横移或钢轨倾覆的影响。当需要考虑轨道结构的横向稳定性及承载能力时，需比较本文所述的最大轮轴横向力限值和满足轨道结构横向稳定性的轮轴横向力限值，将较小者作为安全性评价标准。