牵引电机架悬参数对动车转向架稳定性的影响
徐 坤,曾 京,黄彩虹,祁亚运
(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
根据电机悬挂方式的不同,驱动装置的结构形式通常有轴悬式、架悬式和体悬式之分[1]。在轴悬式中,牵引电机大半质量成为簧下质量,这既增加了车辆对轨道的动力破坏作用,又将轮轨间产生的冲击与振动直接传递给牵引电机,加大了电机的机械载荷,所以该结构一般使用在低速动车上,不宜在高速动车上使用。国内外高速动车上普遍采用的是有利于降低动作用力的架悬式与体悬式。架悬式牵引电机整体悬挂在转向架构架上,属于一系簧上质量,体悬式牵引电机安装在车体底架上,属于二系簧上质量。但由于在体悬式中,万向轴制造工艺要求高,驱动装置结构复杂,制造及维护成本较高[2],架悬式被越来越多地使用,如CRH1、CRH2和CRH3动车组采用架悬式牵引电机。
国内外学者对牵引电机架悬参数对车辆系统动力学的影响进行了广泛的研究。文献[3]对分别采用刚性架悬和弹性架悬方案时机车的横向稳定性、平稳性、轮轴横向力、轮重动态变化等进行了比较研究。研究结果表明,采用弹性架悬方案时机车各项直线高速运行指标均有所改善,且机车的动力学性能对悬挂参数的敏感性减弱。文献[4]对牵引电机刚性架悬与弹性架悬在非线性稳定性、直线运行性能及曲线运行性能进行了比较。研究发现:驱动装置弹性架悬方案可以明显降低机车直线运行的轮轴横向力,改善机车通过大、中半径曲线的横向性能,提高平稳性。文献[5]考虑牵引电机悬挂吊杆橡胶关节的弹性及电机输出轴端与小齿轮连接轴的弹性,分析异步牵引电机谐波转矩对牵引电机传动装置振动的影响。文献[6]提出3个刚体的机车横向振动简单模型,结合轮对横向随机响应的特点,分析不同速度下,驱动装置悬挂参数对机车受迫振动的影响。以上文献大部分都是采用商业软件建模,对架悬参数与转向架蛇行失稳之间的内在关系阐述的不够清楚。文献[7]根据电机架悬特点,推导出动车转向架动力学方程,分析了牵引电机架悬参数对转向架线性临界速度的影响。文献[8-9]针对机车某B0转向架建立了10自由度单转向架横向动力学模型,从动力吸振角度对电机弹性悬挂做出了理论解释。文献[10]不仅分析了牵引电机架悬参数对整车线性临界速度的影响,还利用非线性方法研究架悬参数对整车临界速度的影响,该临界速度在工程应用中也被称为实际临界速度[11]或者失稳速度。在实际工程应用中,由于在评价实际临界速度上的标准不一致[12],往往会得到不一样的实际临界速度。在仿真计算中,应该以非线性临界速度作为评价指标[13]。
本文采用延续算法[14]求得动车转向架在不同架悬参数下的蛇行运动极限环曲线,得到线性临界速度和非线性临界速度,进而研究牵引电机架悬参数对动车转向架稳定性的影响。利用Hopf分叉范式理论分析动车转向架运动系统的三次共振项系数与线性、非线性临界速度的关系。
1 数学模型
客车转向架采用各种型式的定位装置,使轮对通过轴箱与转向架构架之间有不同程度的弹性约束,特别是高速动车组转向架,为了保证获得较高的临界速度,一系定位刚度都比较大,刚度越大,越接近刚性转向架的运动形式,这一点在转向架蛇行运动的试验和稳定性理论计算中都得到了证实[15]。为了便于数学建模,重点突出研究对象,把某型动车转向架简化为刚性转向架,重点研究牵引电机架悬参数对其稳定性的影响。
由于稳定性属于横向动力学问题,与垂向自由度没有关系,又因为本文只研究转向架的稳定性,车体自由度不考虑,仅作为一个参考系沿着轨道方向以恒定的速度运行。考虑到影响架悬动车组转向架蛇行运动稳定性的主要因素是电机的横移模态,电机摇头模态的影响相对较小[7]。基于以上考虑,在进行动力学建模过程中,只考虑刚性转向架的横移(yb)、摇头(φb)和两个电机的横移(ym1、ym2),共4个自由度,其模型如图1所示。
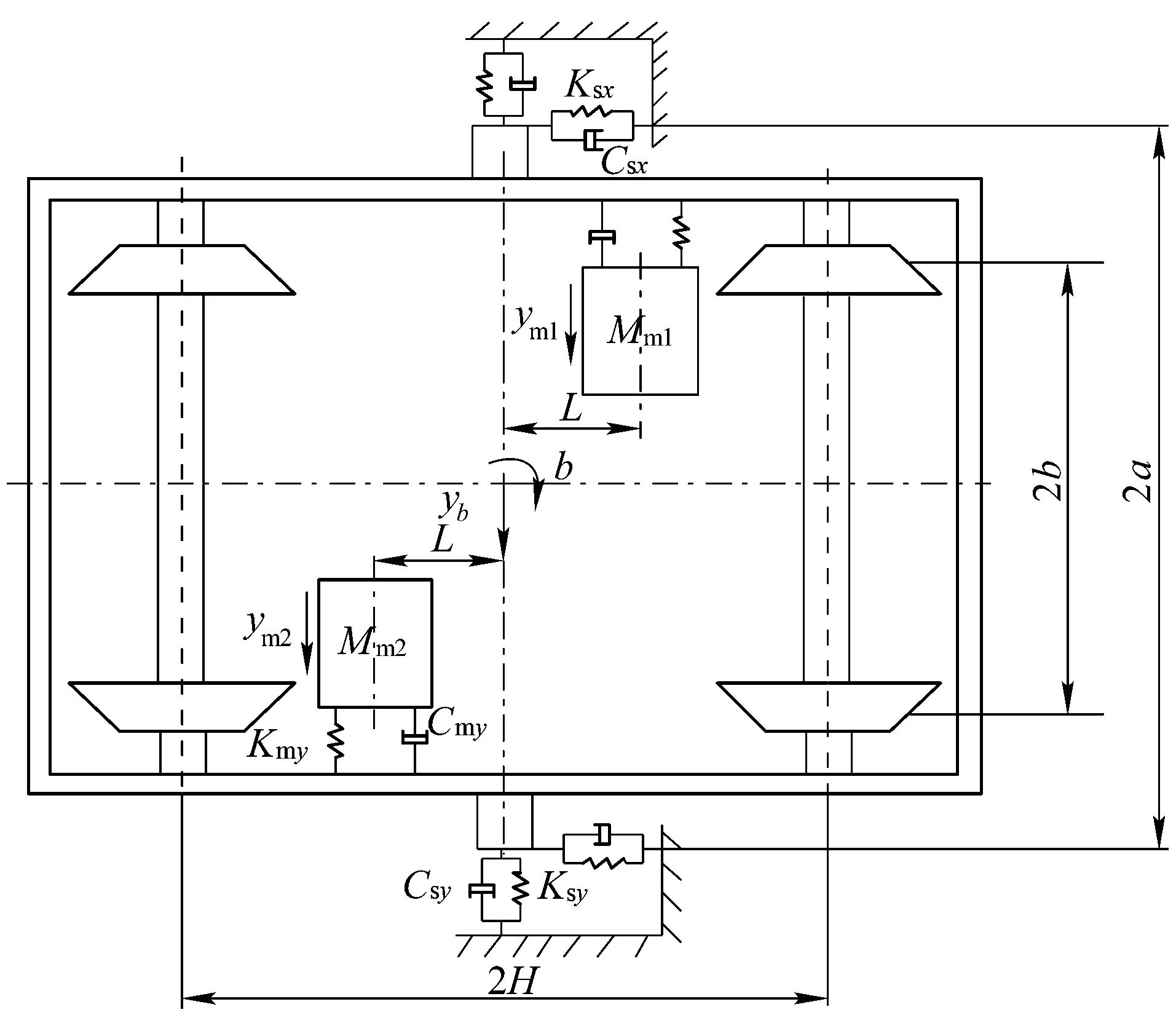
图1 动力学模型
电机1受到的横向力
(1)
电机2受到的横向力
(2)
构架受到的电机的反向横向力
Fb1=-Fm1Fb2=-Fm2
(3)
车轮受到的轮缘力(采用文献[16]中的光滑连续处理)
(4)
除此之外,构架还受弹性约束力及车轮受到横向、纵向蠕滑力和重力复原力和重复原力矩,不考虑车轮受到的自旋蠕滑力。在本系统中,车轮受到的轮缘力是唯一的非线性项。系统微分方程如下:
构架横移
(5)
构架摇头
2Wλbφb
(6)
电机1横移
(7)
电机2横移
(8)
为了便于求解,令
(9)
则式(5)~式(8)可以表示为
dy(1)=y(2)
(10)
Kmy×y(5)+Cmy×y(6)+Kmy×y(7)+
Cmy×y(8)-2(α1×y(1)3+α2×y(1)5)]/Mb
(11)
dy(3)=y(4)
(12)
2Kmy×L2-2Wλb)y(3)-[2Csx×a2+
L×y(5)+Cmy×L×y(6)-Kmy×L×
y(7)-Cmy×L×y(8)]/Ib
(13)
dy(5)=y(6)
(14)
(15)
dy(7)=y(8)
(16)
(17)
以上符号意义及数值见表1。

表1 动力学方程参数意义及数值
由于电机吊挂方式不定,为了便于表达,在下面的论述中使用电机横移频率fmy和横移阻尼比ξmy来代替电机悬挂总的横移刚度Kmy和总的横移阻尼Cmy。Kmy、Cmy与fmy、ξmy的关系如下
(18)
2 转向架蛇行运动Hopf分叉特性
2.1 临界速度的定义及分叉类型
在车辆系统稳定性分析中,主要是通过线性临界速度和非线性临界速度来评价的。在求线性临界速度时,先求线性系统的雅克比矩阵,再求雅克比矩阵的特征值。随着速度的变化,当雅克比矩阵的特征值出现一对纯虚根时,此时速度为线性临界速度。非线性临界速度是根据非线性系统极限环曲线来求得的,非线性转向架系统蛇行运动典型的极限环曲线如图2所示。
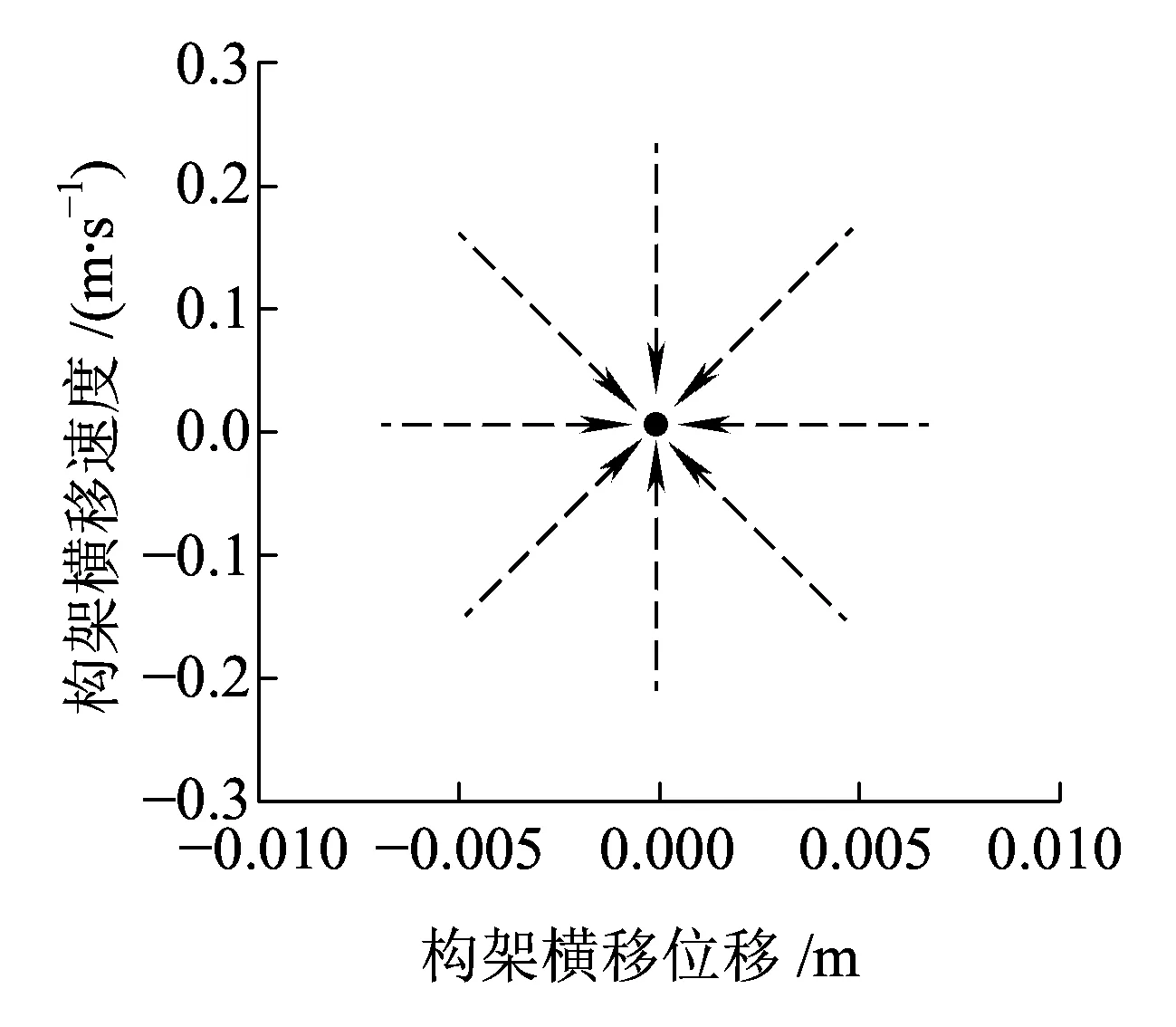
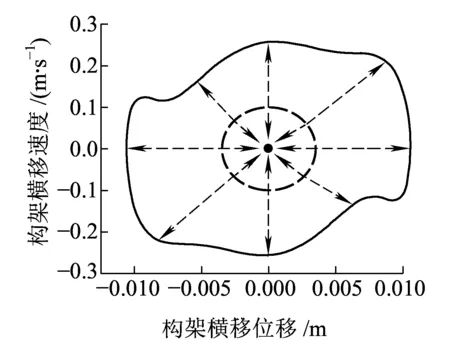
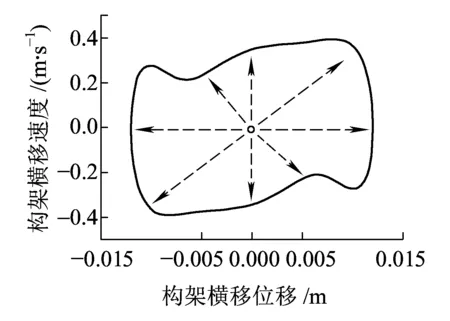
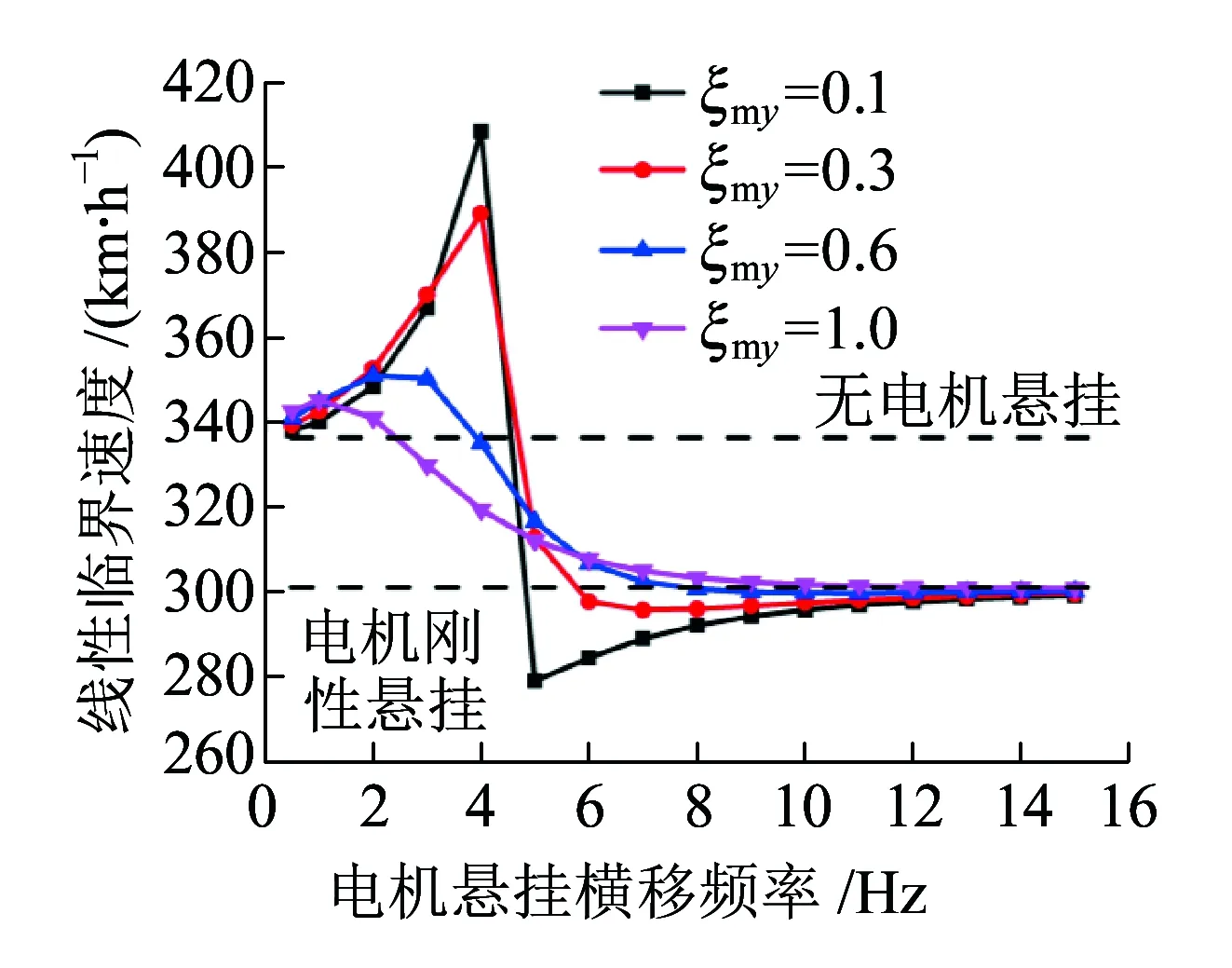
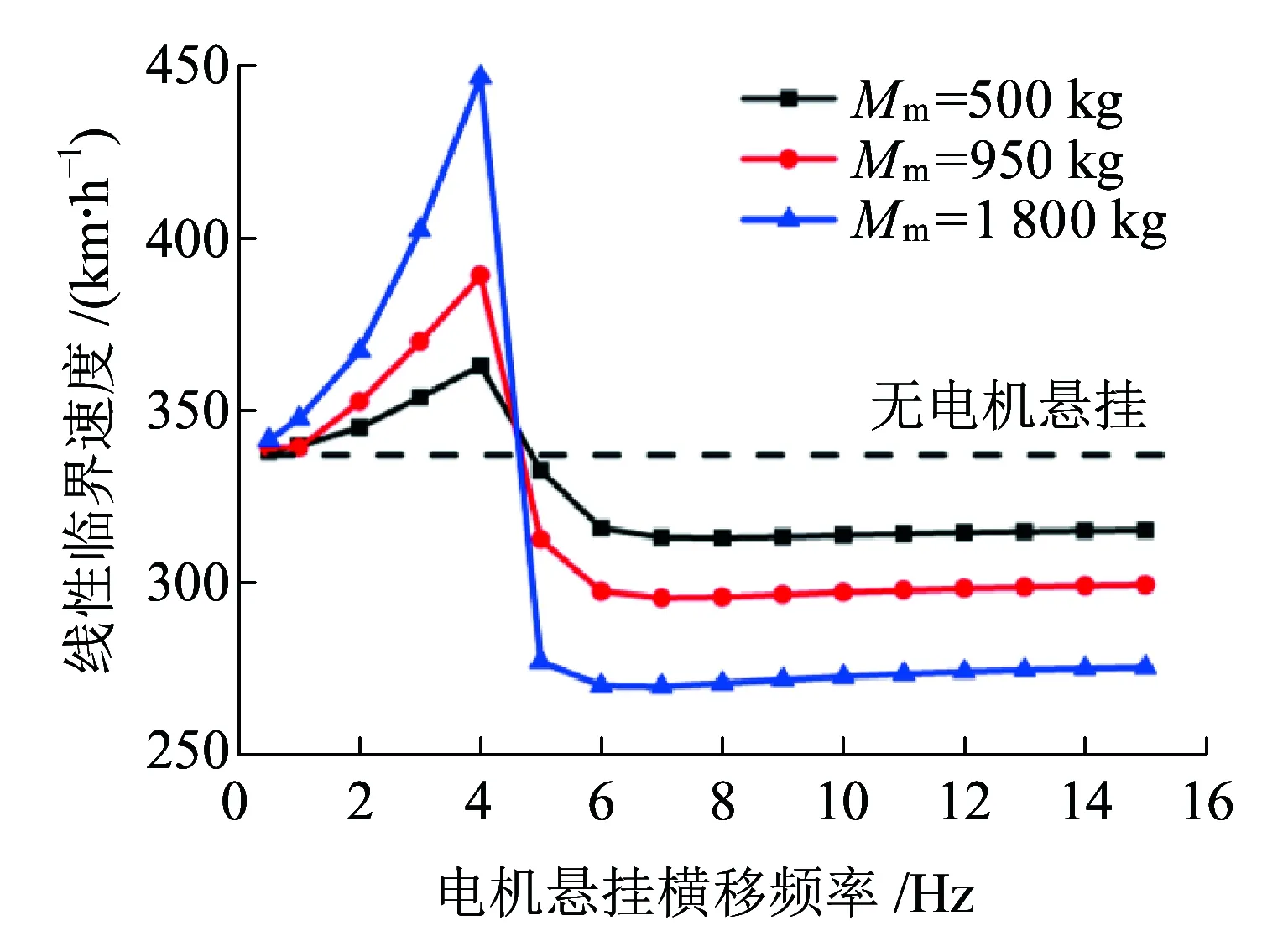
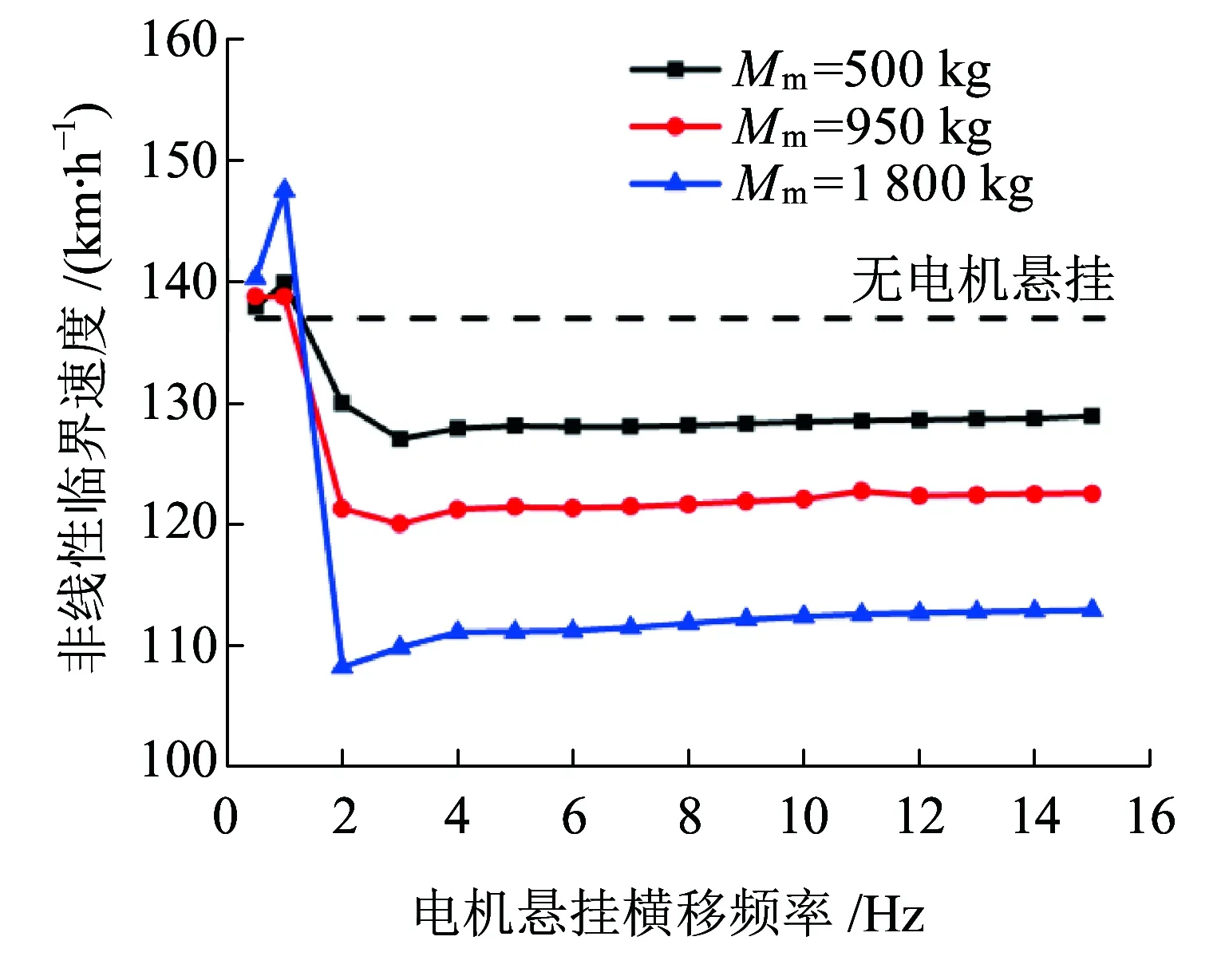
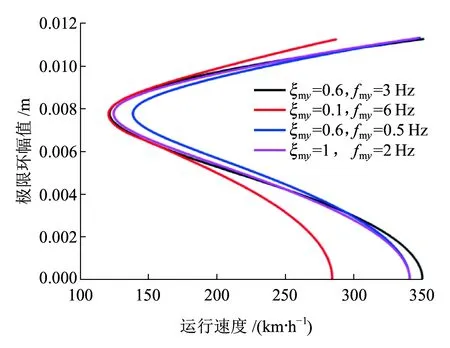
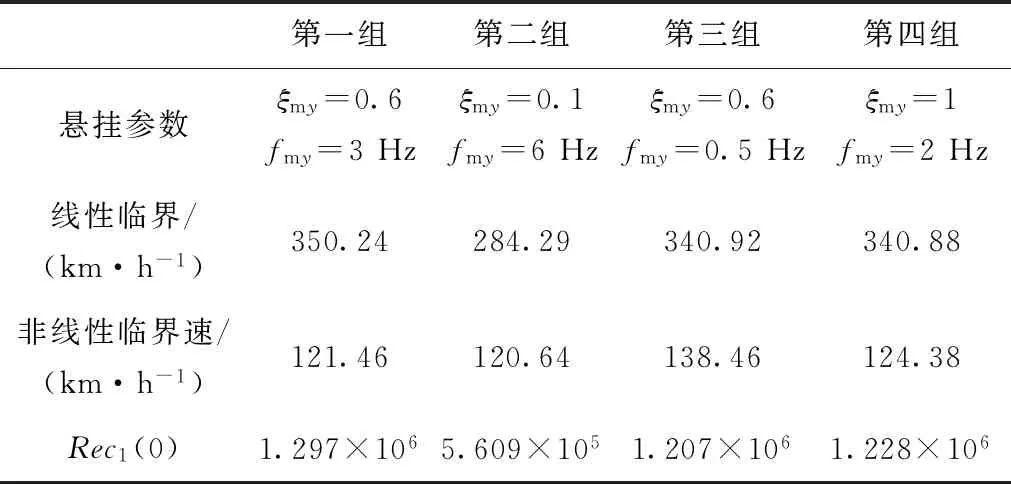
图2中虚线表示不稳定的极限环,实线表示稳定的极限环。V0为线性临界速度,V1为非线性临界速度。当V (a)亚临界Hopf分叉 (b)超临界Hopf分叉 当fmy=1.6,ξmy=0.1时,其余参数数值参照表1中的数值,带入式(10)~式(17),利用延续算法求得转向架蛇行运动极限环曲线,如图3所示。 图3 转向架蛇行运动极限环曲线 由图3可知,系统发生了亚临界Hopf分叉,AB为不稳定极限环,BC为稳定极限环,线性临界速度V0=344.52 km/h,非线性临界速度V0=160.45 km/h。当运行速度以低于非线性临界速度、位于非线性临界速度与线性临界速度之间、高于线性临界速度运行时,构架横移的相平面如图4所示。 当运行速度低于非线性临界速度运行时,整个相平面都是平衡点(0,0)的吸引域,如图4(a)所示;当运行速度在非线性临界速度与线性临界速度之间时,相平面包含一个稳定极限环(实线)、一个不稳定极限环(虚线)和一个稳定平衡点,此时平衡点(0,0)是一个吸引子,整个相平面中不稳定极限环内部区域是平衡点的吸引域,不稳定极限环外部区域是稳定极限环的吸引域,如图4(b)所示;当运行速度高于线性临界速度时,相平面包含一个稳定极限环(实线)和一个不稳定平衡点,此时平衡点(0,0)不再是吸引子,整个相平面中都是稳定极限环的吸引域,如图4(c)所示。 (a)运行速度为100 km/h时构架横移相平面图 (b)运行速度为280 km/h时构架横移相平面图 (c)运行速度为430 km/h时构架横移相平面图 考虑单参数平面自治系统[17] (19) (20) 式中:λ(α)=μ(α)+iω(α);μ(0)=0;ω(0)=ω0>0。 当矩阵A(α)出现一对纯虚根特征值时,发生Hopf分叉,由平衡点分叉出周期解。引入复变量z,系统可表示为 (21) x与z满足 (22) 假设α=0,F(x,α)可表示为 (23) 式中:B(x,x)和C(x,x,x)为对称多重线性型。 (24) (25) 经过推导,系统可简化为只含共振三次项的方程。 (26) 一般称c1(α)为三次共振项系数,Rec1(0)决定了Hopf分叉是超临界分叉还是亚临界分叉。当Rec1(0)>0时,为亚临界分叉,当Rec1(0)<0时,为超临界分叉。 Rec1(0)表达式为 (27) 下面使用Hopf分叉范式理论分析上述参数数值下转向架横移运动分叉特性。 B(ξ,η)=[0 0 0 0 0 0 0 0]T (28) 根据式(27)可得 (29) 可知系统发生了亚临界分叉,与利用极限环图分析得到的结果一致。 电机横移频率fmy为0.5~15 Hz,阻尼比ξmy在0.1~1之间变化,对转向架的线性、非线性临界速度如图5所示。 (a)电机悬挂频率fmy和阻尼比ξmy对转向架线性临界速度的影响 (b)电机悬挂频率fmy和阻尼比ξmy对转向架非线性临界速度的影响 从图5可以看出:转向架的线性、非线性临界速度在无电机悬挂工况均高于电机刚性悬挂工况,但是非线性临界速度的增加幅度要小于线性临界速度的增加幅度。当fmy较小时,转向架线性、非线性临界速度接近无电机悬挂工况;当fmy较大时,转向架线性、非线性临界速度接近电机刚性悬挂工况。当ξmy较小时(比如ξmy=0.1),转向架的线性、非线性临界速度均随着fmy的增大先增加后减小,最后趋于电机刚性悬挂工况,出现这种现象的原因是电机弹性架悬的数学模型本质上属于动力吸振器,轮对的蛇行运动作为激励。随着电机悬挂频率fmy的增加,构架振动响应逐渐减小,所以转向架临界速度逐渐增大,当fmy接近转向架蛇行频率时,构架振动达到最小值,转向架临界速度达到最大值,当继续增加fmy,构架振动忽然增大,转向架临界速度会忽然降低,构架振动最大时,转向架临界速度最低。如果继续增加fmy,构架振动趋于稳定,转向架临界速度也趋于稳定。当ξmy较大时(比如ξmy=1),转向架的线性、非线性临界速度均随着fmy的增大而减小,最后也趋于电机刚性悬挂工况。值得注意的是,当ξmy>0.3时,转向架的非线性临界速度随fy的变化规律几乎一致。 当电机悬挂横移阻尼比ξmy=0.3时,横移频率fmy在0.5~15 Hz之间变化,电机质量Mm分别取500、950、1 800 kg,转向架的线性、非线性临界速度如图6所示。 (a)电机悬挂频率fmy和电机质量Mm对转向架线性临界速度影响 (b)电机悬挂频率fmy和电机质量Mm对转向架非线性临界速度影响 从图6可以看出,当fmy较小时(比如fmy=0.5),不管电机质量多大,转向架的线性、非线性临界速度都与无电机悬挂工况几乎一致。当fmy较小时,电机质量越大,转向架的线性、非线性临界速度越大,相反,当fmy较大时,电机质量越大,转向架的线性、非线性临界速度越小,这也说明了对于大质量电机,弹性悬挂的必要性。 利用转向架的极限环曲线很容易求得转向架的线性、非线性临界速度,但是利用延续算法求极限环曲线比较费时间。由于微分方程的三次共振项系数实部能判别系统分叉特性,通过微分方程的三次共振项系数实部比较系统的线性、非线性临界速度。选取了四组有代表性的悬挂参数,在这四组参数下,转向架横移运动的分叉曲线如图7所示(为了表达方便,不稳定极限环也用实线表示),其Rec1(0)值见表2。 图7 四组悬挂参数下的转向架横移极限环曲线 表2 四组悬挂参数下的Rec1(0)的比较 从图7和表2可以看出,线性临界速度相差较大,非线性临界速度不一定相差很大(第一组与第二组比较);线性临界速度相差较小,非线性临界速度不一定相差很小(第三组与第四组比较)。线性临界速度大,非线性临界速度不一定大(第一组与第三组比较)。所以,线性临界速度与非线性临界速度之间没有必然的关系。但是通过比较Rec1(0),可以得到这样一个规律:每组的线性临界速度与非线性临界速度相差越大,Rec1(0)值越大,这个规律反映在极限环曲线上就是极限环曲线越往左“扭曲”,其Rec1(0)值越大,这与文献[18]得出的结论是一致的。因此在确定悬挂参数时,在线性临界速度比较接近的几组参数中,可以直接通过比较Rec1(0)值来比较非线性临界速度大小,而不必画出极限环曲线,这样可以节约大量的计算时间。 (1)在选取电机悬挂参数时,要兼顾转向架的线性临界速度和非线性临界速度,因为线性临界速度高,非线性临界速度不一定高。 (2)相对于转向架的线性临界速度,其非线性临界速度对电机悬挂参数不敏感,特别是当电机悬挂频率fy、阻尼比ξy较大时,非线性临界速度基本上不受悬挂参数的影响。 (3)电机质量对转向架的线性、非线性临界速度都有较大的影响,但线性临界速度受其影响程度要比非线性临界速度大。 (4)转向架的线性临界速度与非线性临界速度相差越大,系统方程在分叉点的三次共振项系数实部(即Rec1(0))越大。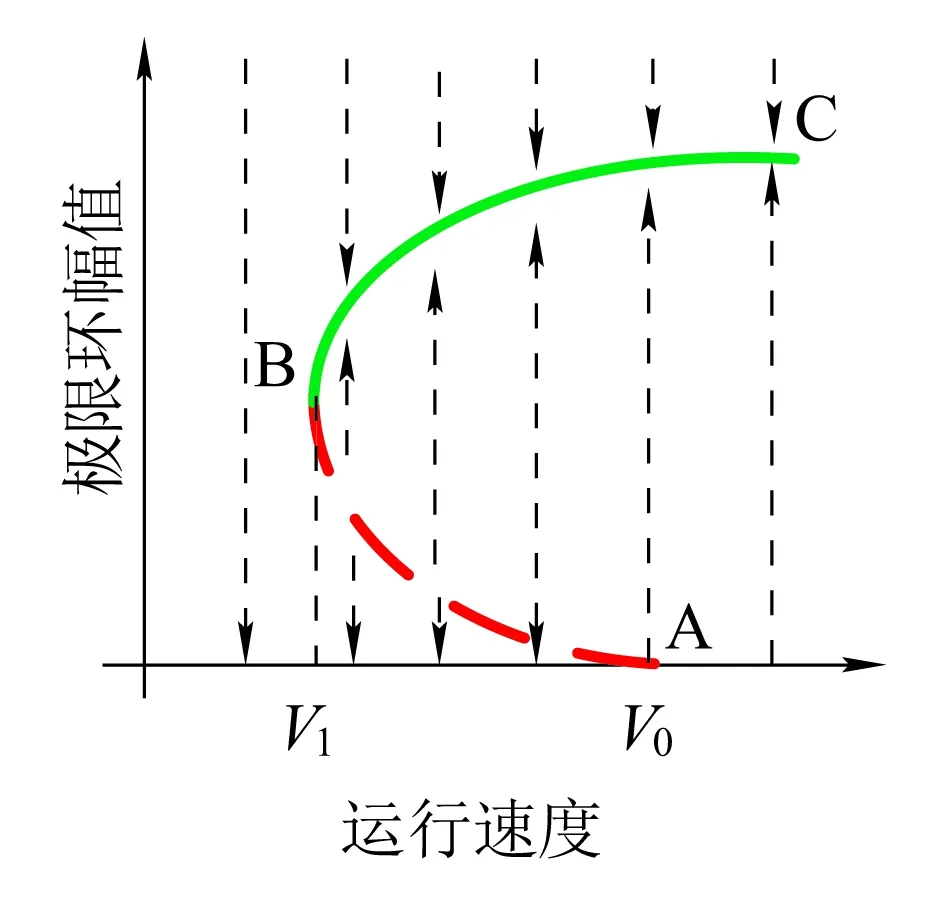
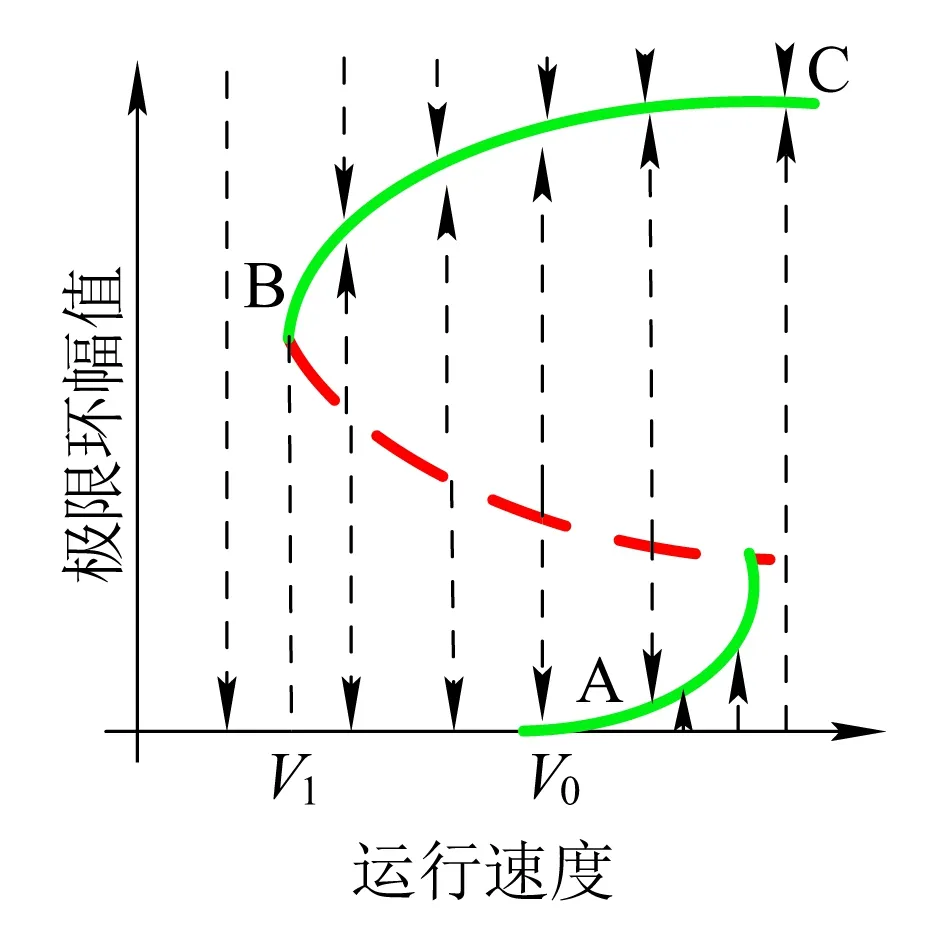

2.2 利用Hopf分叉范式理论判别分叉类型
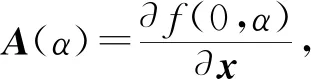


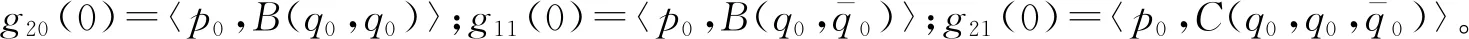
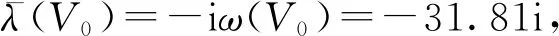
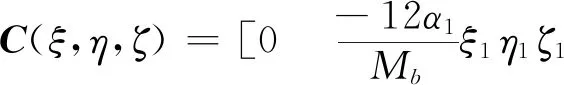
3 电机架悬参数对动车转向架稳定性的影响
3.1 电机横移频率fmy和阻尼比ξmy对转向架稳定性的影响

3.2 电机横移频率fmy和电机质量Mm对转向架稳定性的影响
4 三次共振项系数实部与线性、非线性临界速度之间的关系
5 结论

