基于GIS空间分析建模的区间线路走向自动生成方法

谭衢霖，李 然，董晓峰，杨 敬，秦晓春

(北京交通大学 a.土木建筑工程学院，b.线路工程空间信息技术研究所，北京 100044)

铁路选线是一个多目标决策问题[1-2], 不仅要实现交通运输、满足客货运量的需要，还要考虑生态环境保护、工程经济、安全等诸多因素和目标，涉及的各种因素都可能对线路方案的建设成本或费用高低存在一定的影响.为了贯彻“规划选线、成本选线、重点工程选线、环保选线、地质选线及安全选线”等选线原则与理念，将“综合经济成本”理念融入铁路选线研究，全面综合地分析考虑诸多影响因素和目标是经济不断发展与生态环境可持续发展的前提和要求.例如，文献[3-5]从环境的适应性、工程的可靠性、投资的合理性、兼顾多方利益、可持续科学发展观等方面，对铁路选线的制约因素进行了研究.以前，铁路选线设计主要依赖于设计工程师的知识与经验,结合地形、地质及环境影响等因素，通过人工方式选出最终线路空间位置,存在工作强度大、比选方案有限、选线设计周期长等缺陷.随着我国铁路建设由东部平原向西部复杂艰险山区转移,高度复杂的地理环境使空间线位设计变得更加困难,选线周期大大延长,亟需一种高效率的选线方法克服上述困难.以地理信息系统(Geographic Information System，GIS)为平台，利用空间分析技术，可以充分结合铁路选线区域内的地形、地质、地物和环境数据，将铁路选线影响因素按照影响程度和相对重要性以数字定量信息的形式集成到分析模型中[6-8].例如，文献[9-11]等探讨了基于GIS的铁路选线设计应用分析模型，提出了铁路定线方案综合分析评价模型.文献[12]综合考虑了坡度、房屋拆迁、土地利用、公路4个影响因素，对如何选取符合各项指标的最优线路进行研究，认为基于GIS的铁路选线在局部方案上可节约90%以上的线路平面设计时间.

文献[13]认为，智能选线的发展将更多地结合GIS和建筑信息模型(Building Information Modeling，BIM)等技术平台，摆脱传统选线方法存在的投入大、周期长、精度低、主观性强等弊端，实现快速、精准的智能选线，提高工作效率.文献[14]提出了一个结合人工智能、地理信息等技术开发的铁路三维空间智能选线系统.实践表明其能够在给定选线参数、约束条件的基础上,在选线区域内快速优选多个走廊带,并给出合理的推荐方案,可有效提高选线工作的效率与质量,节约工程投资.文献[15]基于GIS和决策支持系统(Decision Support System，DSS)技术，基于GIS的空间数据叠置法和强大的空间分析功能，在图层叠置中引入权重，实现多因子的综合评价，从而建立铁路绿色选线决策支持系统.

如何实现线路智能优化，从连接起终点的无限多个线路方案中找到一条综合最优的线路，是实现铁路数字化选线的一项关键技术.基于GIS的区间铁路选线空间信息分析模型，可有效克服选线设计中方案有限、评价指标少、选线效率低、决策周期长以及对采用方案的科学性缺乏有效论证等问题.本文作者在GIS空间分析技术支持下，综合考虑分析铁路选线区域内的地形、地理环境和生态环境影响，以坡度、坡向、土地利用、植物群落、水域和湿地、道路、文物古迹和建筑用地等8个影响因素作为铁路选线的单成本因子，以辽宁省康平-法库区间铁路线路选线为试验段，建立了以综合成本最低为目标的区间铁路选线空间信息分析模型.

1 成本距离最优路径模型

基于成本距离最优路径模型分析技术的基本思路是：针对影响选线的多种因素(多种约束条件，主要包括水域和湿地、植物群落、坡度、文物古迹、土地利用、道路、建筑用地和坡向等)，分别建立空间数字要素图层；然后对各图层中每个栅格对铁路线路的建设成本给出量化的影响程度，其值即为空间数字图层栅格单元的属性值(表示在该栅格单元内布线成本的高低)；再通过空间叠加分析，将各个因素的栅格属性值进行线性代数运算，获得综合成本栅格图层.把综合成本与欧几里德空间距离计算结合，形成成本距离，就可以由GIS的最优路径搜索算法生成连接起终点的最优路线.

1.1 成本距离

成本距离是指通过成本因素加权后距源位置的一种距离(或者说是累积行程成本)，它是以成本单位表示的距离，而不是以地理单位表示的距离.成本距离方程可以表示每个栅格单元到最近源的最小累计成本距离，目的是用来识别与选取目标点距源点之间的最小成本费用方向和路径.成本距离的计算方式见图1，利用结点/连接线方式表达：每个像元的中心被视为结点，并且结点间通过连接线使其相连，每条连接线都赋有关联的阻抗值.有两种计算方式：

1)直接相邻成本距离计算方式，见图1(a).设从单元i前往上下左右4个直接相邻的单元i+1，其成本距离的计算公式为：Ni+1=Ni+(Ri+Ri+1)/2,其中Ni和Ri分别为所在单元i的累计费用和阻抗值.

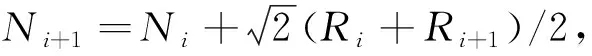
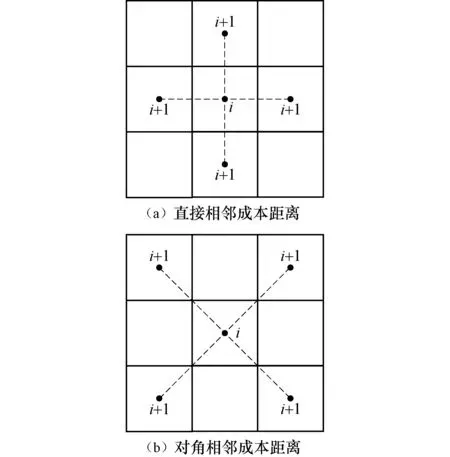
图1 成本距离计算方式Fig.1 Calculation method of cost distance

1.2 成本因素

综合成本是指综合考虑多种因素，对线路走向方案的建设成本或费用影响程度的一种总的度量.线路走向方案综合成本高，意味着建设费用高、综合效益低；线路走向方案综合成本低，意味着建设费用低、综合效益高.综合成本对铁路选线走向研究贯彻“规划选线、成本选线、重点工程选线、环保选线、地质选线及安全选线”等原则与理念，提供了一种综合、定量的评判标准和手段.本文主要考虑的是“非不良地质区域”或“非复杂地质条件”主控下的生态环保线路选线，因此主要选择坡度、坡向、土地利用、植物群落、水域和湿地、道路、文物古迹和建筑用地等8个影响因素，作为区间铁路选线的综合成本考虑因素.

1)坡度：影响着工程的难易程度，也决定着工程的安全系数.坡度越陡，工程建设的投入及施工难度越大，对工程建成后的安全保障要求越高.

2)坡向：与光照情况紧密相关，真接影响植被群落的分布，从而给工程建设带来生态环境影响.

3)土地利用：其类型不同，涉及征地与拆迁问题，施工难易程度、对生态系统平衡的影响也不同.

4)植物群落：不同的植物群落自我修复能力不同，对人为干扰的抵抗能力也就不同.自我修复能力及对人为干扰的抵抗能力差的植被群落称为生态敏感性高的群落，而线路工程建设要保护生态敏感性高的群落.

5)水域和湿地：易受到人类不良活动的影响而造成不可恢复的破坏，且对工程施工也会造成困扰.

6)道路：铁路的选线应当与道路保持一定的距离，以避免相互干扰.

7)文物古迹：铁路在选线规划中应当考虑对文物古迹产生的振动及噪声影响.

8)建筑用地：与其他建筑物之间应当保持一段距离，避免线路噪声干扰.

1.3 最优路径算法

最优路径也称最佳路径.最佳路径分析一直是计算机科学、运筹学、交通工程学及地理信息科学等学科的研究热点.这里的“最佳”包含很多含义，不仅指一般地理意义上的距离最短，还可以是成本最少、耗费时间最短、资源流量(容量)最大、线路利用率最高等标准.无论判断标准和实际问题中的约束条件如何变化，其核心实现方法都是最短路径算法.下面结合地理空间距离和其他影响因素的成本综合考虑，以“综合成本”最低为最优路径的判断标准.最短路径常用的实现算法有Dijkstra算法[16]、Floyd算法和A*算法等，其中Dijkstra算法是解决最佳路径问题的最好方法，也是目前公认的解决最短路径问题的经典且有效的算法.在该算法中，采用逐步构造最优解的方法，在每个阶段都做出一个在当前情况下看上去最优的决策，直至得到最后结果.该算法的主要特点是：以起始点为中心向外层扩展，直到扩展到终点为止.Dijkstra算法的思想是：令G=(V,E)为一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合S(初始时S中只有源点，以后每求得一条最短路径,就将它对应的顶点加入到集合S中，直到全部顶点都加入到S中)；第二组是未确定最短路径的顶点集合U.在加入的过程中，总保持从源点V到S中各顶点的最短路径长度不大于从源点V到U中任何顶点的最短路径长度.

Dijkstra算法步骤如下：

1)创建两个集合，S集合和U集合.S集合保存所有已生成而未考察的节点，U集合中记录已访问过的节点.

2)访问路网中距离起始点最近且没有被检查过的点，把这个点放入S集合中等待检查.

3)从S集合中找出距起始点最近的点，找出这个点的所有子节点，把这个点放到U集合中.

4)遍历考察这个点的子节点.求出这些子节点距起始点的距离值，放子节点到S集合中.

5)重复第2)和第3)步,直到S集合为空，或找到目标点.

图2为从A点至D点最优路径的Dijkstra算法图，表1为其算法步骤.

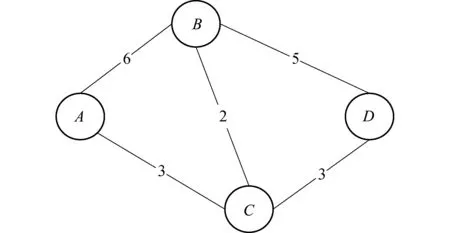
图2 Dijkstra算法图Fig.2 Dijkstra algorithm diagram

2 康平-法库铁路选线GIS建模

康平县隶属辽宁省沈阳市，地处辽河流域，北纬42°31′～43°02′，东经122°45′～123°37′之间，东隔辽河与铁岭市昌图县相望，西邻阜新市彰武县，南接法库县，北与内蒙古科左后旗毗邻，是沈阳经济区北部腹地的重要支撑点之一，是沈阳城市发展四大空间战略的向北门户，是环渤海经济圈及辽宁中部城市群上的重要节点，同时又是辽、吉、蒙两省一区结合部的区域中心.法库县位于辽宁省北部，长白山山脉与阴山山脉余脉交会处，在辽河右岸，南与沈阳隔辽河相通，北与康平县、昌图县、开原市接壤，东与调兵山市、铁岭县毗邻，西与新民市、彰武县相接，是沈阳经济区辐射东北及蒙东地区的重要节点.现拟建一条康平站至法库站的区间铁路，GIS选线建模流程，如图3所示.

表1 算法步骤

2.1 选线因素赋值

采取德尔菲法和层次分析法(Analytic Hierarchy Process，AHP)相结合的方式，确定每个因素的成本值.德尔菲法和层次分析法是运筹学理论中得到广泛应用的两种方法.德尔菲法也称专家调查法，本质上是一种反馈匿名函询法，其大致流程是：在对所要预测的问题征得专家的意见之后，进行整理、归纳、统计，再匿名反馈给各专家，再次征求意见，再集中，再反馈，直至得到一致的意见.层次分析法是把一个复杂的多目标决策问题作为一个系统，将目标分解为多个小目标或准则，进而分解为多指标(或准则、约束)的若干层次，通过定性指标模糊量化方法算出层次单排序(权数)和总排序，以进行目标(多指标)、多方案优化决策.

因素成本值取1、3、5、7、9储存在各个地图的像元中，表示在该像元内布线成本的高低，即值越高表示在此像元内布线的综合成本越高，值越低表示在此像元内布线的综合成本越低(见图4).

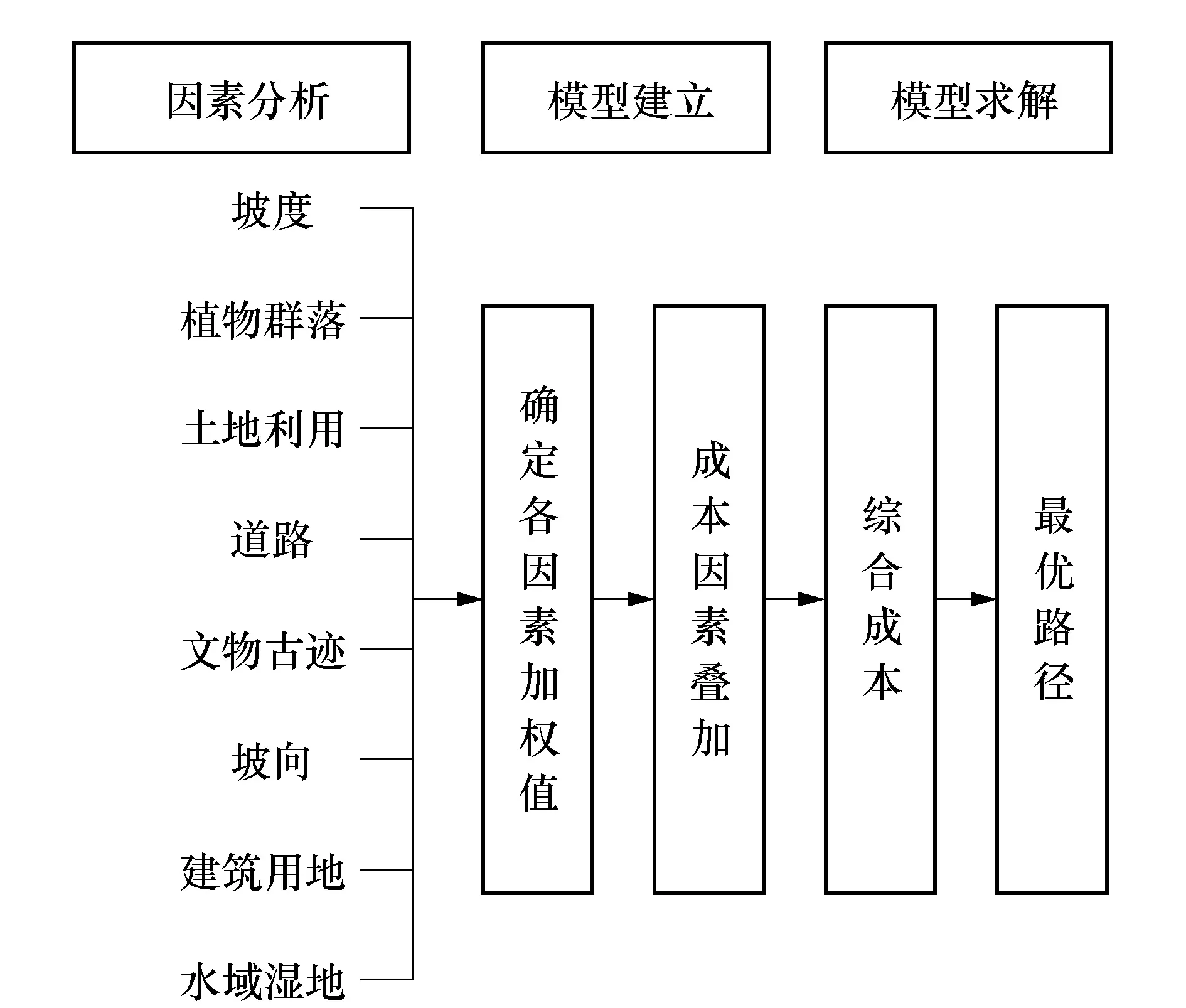
图3 GIS选线建模流程Fig.3 Modeling process of GIS route selection

1)水域和湿地按缓冲区进行赋值.在接近水域和湿地地段施工，对水域和湿地造成破坏大，同时产生的工程费用高，因此越接近水域和湿地成本值越高，水域和湿地本身成本值取9，0～50 m缓冲区成本值取7，50～100 m缓冲区成本值取5，100～200 m缓冲区成本值取3，>200 m缓冲区成本值取1.水域湿地分级赋值如图4(a)所示.

2)植物群落按生态敏感性的高低进行赋值.在受到外界干扰时，生态敏感性越高的植物群落越容易产生生态环境问题，因此生态敏感性越高成本值越高.杉木林、加杨林、枫杨林、板栗林等的成本值取9，紫叶李林、桂花林、马尾松林等的成本值取7，灌丛、油茶、林竹林等的成本值取5，水生植物、旱作植被、水稻等成本值取3，无植物、忙草地、荒草地等的成本值取1.植物群落分级赋值如图4(b)所示.

3)坡度按其大小进行赋值.坡度越大，工程费用越高，成本值越高.>20°成本值取9，15°～20°成本值取7，10°～15°成本值取5，5°～10°成本值取3，0°～5°成本值取1.坡度的分级赋值如图4(c)所示.

4)文物古迹按缓冲区进行赋值，在接近文物古迹等敏感地区修建铁路，无论在施工还是运营阶段，都会对其产生影响，因此越接近文物古迹等敏感地区成本值越高.0～200 m缓冲区成本值取9，200～300 m缓冲区成本值取7，300～350 m缓冲区成本值取5，350～400 m缓冲区成本值取3，>400 m缓冲区成本值取1.文物古迹分级赋值如图4(d)所示.

5)土地利用按其对生态平衡的不同作用及对施工的干扰程度进行赋值，沟渠、河流、湿地、滩涂、坑塘等成本值取9，林地、果园、灌木林地等成本值取7，水浇地、水田、旱地等成本值取5，草地、农村宅基地等成本值取3，公路用地、农村道路、工业用地等成本值取1.土地利用分组赋值如图4(e)所示.

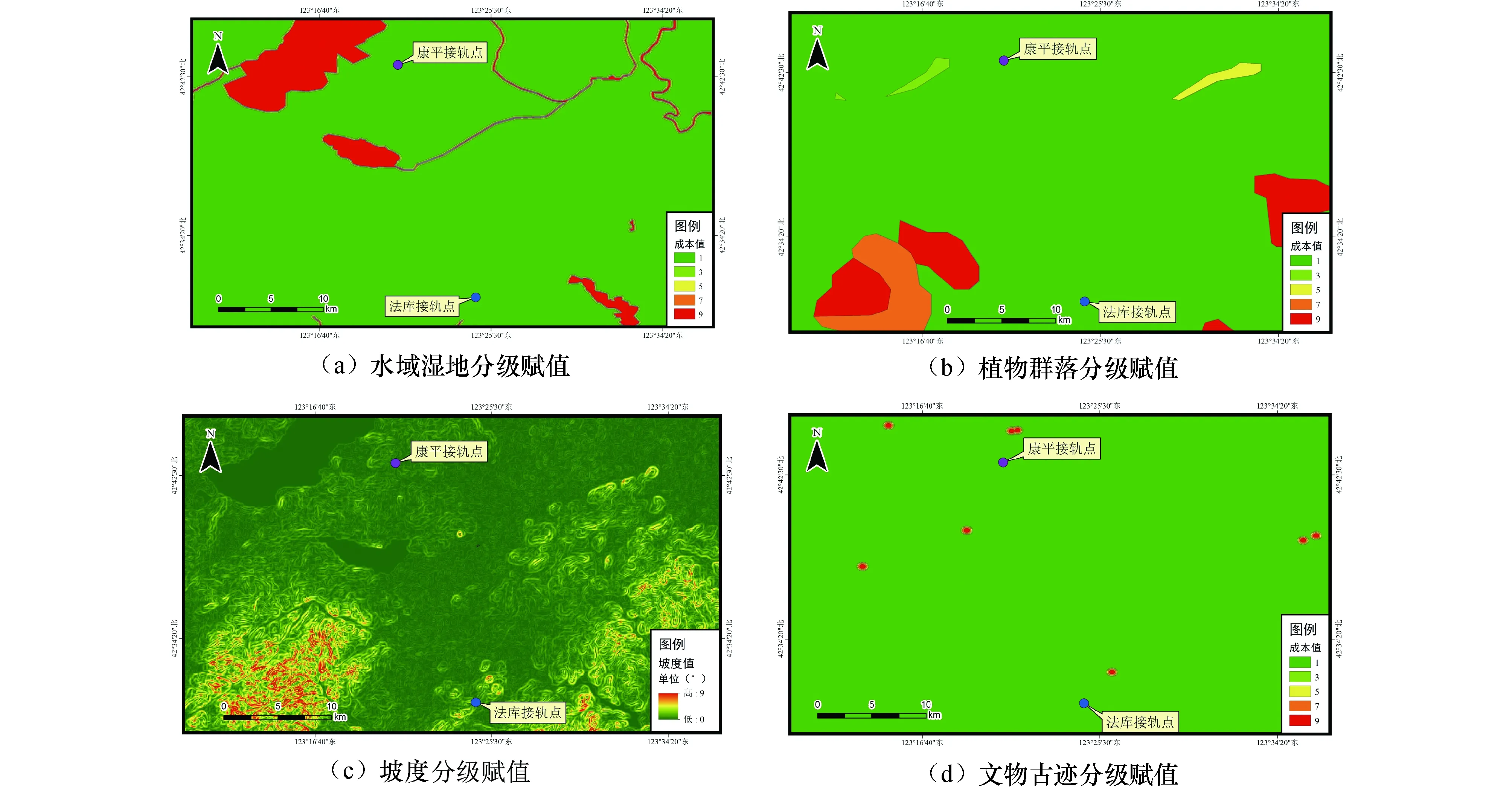
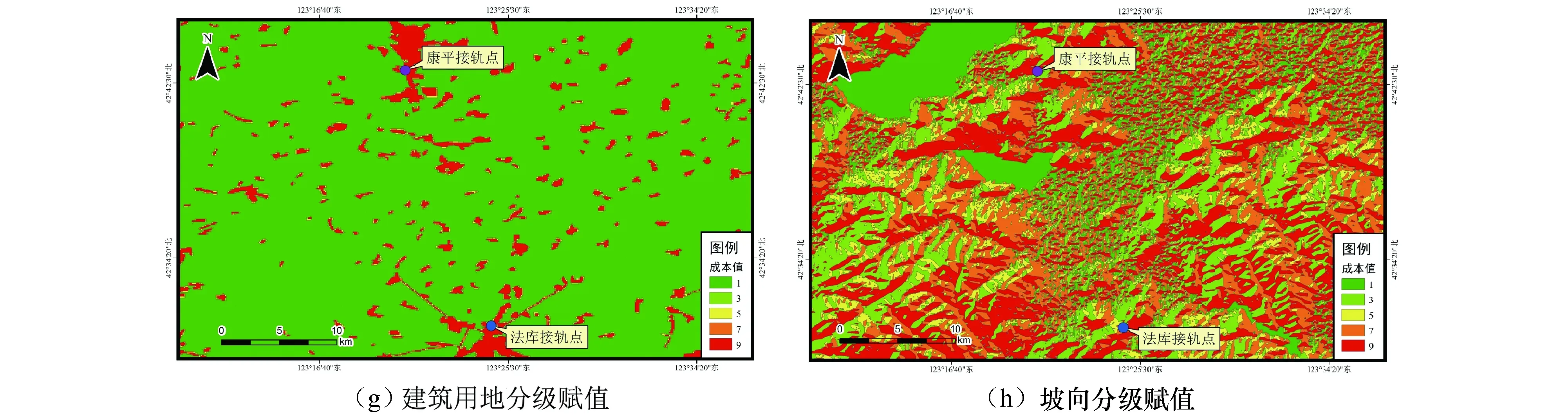
图4 各因素分级赋值Fig.4 Factor grading assignment graphic

6)道路按缓冲区进行赋值.越接近道路相互影响越严重，因此成本值越高.道路本身成本值取9，0～10 m缓冲区成本值取7，10～20 m缓冲区成本值取5，20～50 m缓冲区成本值取3，>50 m缓冲区成本值取1.道路分级赋值如图4(f)所示.

7)建筑用地按缓冲区进行赋值.越接近建筑视觉噪声等干扰越严重，因此成本值越高.建筑本身成本值取9，0～20 m缓冲区成本值取7，20～40 m缓冲区成本值取5，40～60 m缓冲区成本值取3，>60 m缓冲区成本值取1.建筑用地分级赋值如图4(g)所示.

8)坡向按植被光照情况进行赋值，东南-西南(112.5°～247.5°)成本值取9，东-东北(22.5°～112.5°)成本值取7，北(337.5°～0°～22.5°)成本值取5，西-西北(247.5°～337.5°)成本值取3，平面成本值取1.坡向分级赋值如图4(h)所示.

2.2 成本因子权重

采用德尔菲调查法，邀请5位相关专家对8个成本因子中每两两因子的相对重要性做出评价，计算得出各个评价因子的权重值，如表2所示,并经检验确定其可以作为评价的权重使用.

权重确定后，对多目标决策模型成本，因素进行线性加权叠加运算，计算出综合成本.其计算式为

式中：i为各成本因素编号；k为成本因素分级赋值的编号；n为成本因素总数；Ci为第i个成本因素的综合值；Sk为第k个成本因素的权重；Wik为第i个分级赋值单元的第k个成本因素的综合值.

2.3 空间选线建模

首先，针对水域湿地、植物群落、坡向、坡度、建筑用地、土地利用、文物古迹和道路影响选线的8个影响因素，建立空间栅格数字图层；然后，就各图层中每个栅格对铁路选线的成本进行属性赋值；再通过加权叠加，将各个因素的栅格属性值进行栅格运算，得

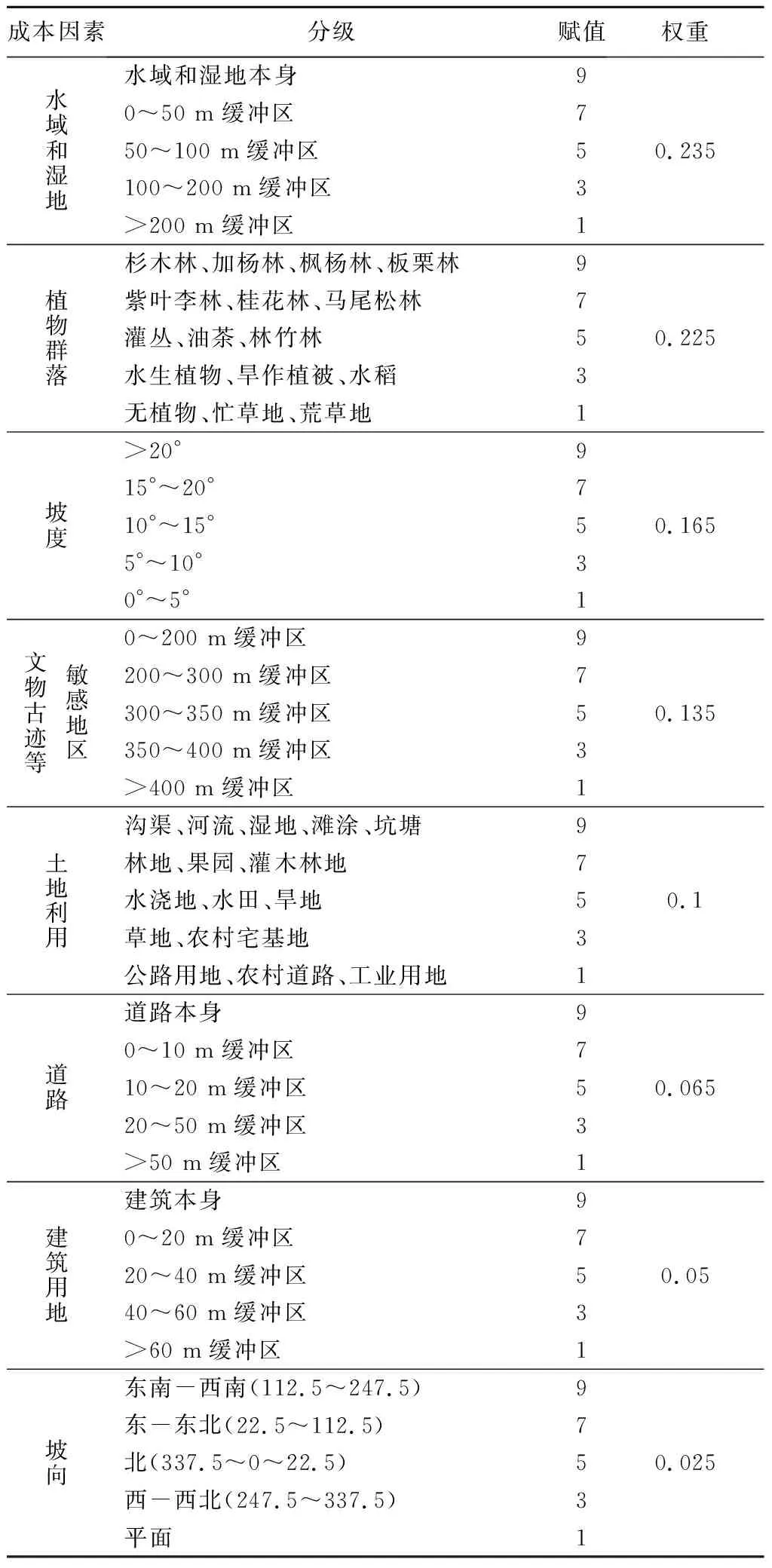
表2 成本因素的分级、赋值与权重

出综合成本空间栅格图层.当综合成本建立后，就可以通过基于成本距离模型的最优路径分析技术，自动生成连接起终点的最优路径.最后，可将自动生成的最优线路转为矢量数据，对线形进行完善.图5所示为GIS选线建模流程，图6为模型选线结果.

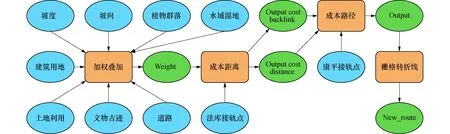
图5 GIS建模流程Fig.5 Flowchart of GIS modeling

由图6可以看出，选出的线路穿越地势较平坦的地区，远离了陡坡、沟坎，降低了工程地质的难度，提高了工程的安全系数；远离湿地和水域，减小了对湿地和水域的影响，保护了水域和湿地，同时减少了工程数量，降低了综合成本；远离生态敏感性高的植物群落地区，保护了生态系统；经过草地、旱地等铁路建设成本较低的地区，远离施工难及对生态平衡有重要影响的地块；选择对植被群落光照影响少的坡向，从而有利于生态系统的保护；与道路保持一定的距离，降低干扰；与文物古迹保持一定的距离，重视对历史文物的保护；与其他建筑保持一定的距离，避免或降低了噪声干扰.由分析可知，上述建模自动生成的线路确实经过了综合成本值最低的区域，选线结果符合综合经济成本最低的规划目标.最后，将生成的最优路径转为矢量要素文件，进一步可转换为CAD的DWG格式文件，可设计出既满足综合经济成本最低又符合工程设计线形要求的路线.

3 结论与讨论

在GIS空间分析技术支持下，综合考虑分析铁路选线区域内的地形、地理环境和生态环境影响，将坡度、坡向、土地利用、植物群落、水域和湿地、道路、文物古迹和建筑用地等8个影响因素，作为铁路选线的单成本因子，以辽宁省康平-法库区间铁路线路选线为试验段，建立了以综合成本最低为目标、可以自动生成最优线路路径的区间铁路选线空间信息分析模型.康平-法库区间铁路选线GIS建模应用表明，采用基于成本距离模型的最优路径技术，是解决铁路选线多目标约束条件下自动进行空间线路搜索决策的可行方法，可有效克服选线设计中方案有限、评价指标少、选线效率低、决策周期长以及对采用方案的科学性缺乏有效论证等问题，具有工程实用性.建立的区间铁路选线空间信息分析模型可以作为一个专门的空间选线工具模块，以批处理工作流方式运行，具有可移植、能高效自动生成区间线路路径的优势.需要说明的是：

1)本文工作是针对确定的相邻两点之间(可以是区间的起点和终点之间，也可以是某两个确定的区间控制点之间，还可以是某站点与近邻的控制点之间)的最优线路走向自动确定并生成的方法.理论上，两点之间的线路路径有无数条，采取的方法是在这无数种可能的路径(走向)中，按照设定的最小综合费用成本目标来确定并生成最优路径.

2)地质因素是选线重要的影响因子，特别在复杂不良地质区域，线路选线需要重点考虑，进行“地质选线”.但是本研究主要考虑的是“非不良地质区域”或“非复杂地质条件”主控下的生态环保线路选线.即使在复杂地质条件下，GIS空间分析建模线路优选方法仍然可以参照应用，只需把地质因素因子作为关键成本因素增加到地理空间信息模型中，再按照上述方法和流程进行应用.本质上，这里只是提供了一种“基于GIS空间分析建模的区间线路走向自动生成方法”，在具体应用中，成本因素的增加或减少需要结合具体工程案例的实际情况进行.

3)“铁路选线空间信息分析模型”是指这类基于GIS空间分析技术的铁路选线方法模型，但具体如何实现有很多种途径.“成本距离最优路径模型”是这类“铁路选线空间信息分析模型”的一种具体的、在本文中应用的方法模型，而Dijkstra算法(最优路径算法)是“成本距离最优路径模型”实现中的最短路径求算解法.