基于Dijkstra算法优化的城市交通路径分析

吴红波，王英杰，杨肖肖

(1. 陕西理工大学 地理科学系，陕西 汉中 723000；2. 西北大学 陕西省地表系统与环境承载力重点实验室，西安 710127；3. 北京交通大学 土木建筑工程学院，北京 100044)

路径分析是城市交通网络分析的研究内容之一，也是地理信息系统(Geographic Information System，GIS)空间分析功能的组成部分，并在城市道路管理、网络通信、交通规划等方面得到广泛应用[1].路径分析的核心是最短路径、最佳路径的求解，而路径优化是利用运筹学规划模型使道路网络使用、车辆调度、货物配送等的运行效率达到最优.

地理信息系统是将关系数据库管理、图形算法、空间插值、区划和网络分析等功能集成于一体，能有效管理地理空间数据，其空间分析可为智慧交通建设提供技术支持.近年来，随着网络信息、物联网和移动互联技术的日益发展，GIS技术被应用于物流配送、交通规划、道路选址、路径优化研究[2]，使得海量地理信息的提取、表现和传输任务变得简单易行.在现实中，最短路径指的是带权图上的最短路径问题，不仅是欧氏空间中的距离最短，也可以是时间最短、费用最少、线路使用率最优[3].Papinski等[4]考虑距离、行程时间、速度统计、交叉口数、匝数、停车标志/停车灯数量和路线迂回等变量，借助GIS路径分析工具箱，对比分析时间最短和距离最短的优化时间.Yang等[5]基于GIS网络分析工具模块,对车辆规划路线和固定路线的运输服务范围、运营成本、成本效益进行综合分析.Huang[6]利用GIS网络分析和层次分析法(Analytic Hierarchy Process，AHP),分析了道路网络中的每个链路的影响因素，结合危险品运输车的安全性和运输成本，通过成本函数模型,量化出每个运输路线的适用性.针对小学生从学校到家庭住处的行走路线，Duncan等[7-8]联合GPS(Global Positioning System)和GIS技术,分析了选线过程中行驶距离、道路节点、道路拥堵的影响，帮助人们快速确定最短路径.关于最短路径分析算法研究已有较多报道[9-10]，Bellman算法、Dijkstra算法、Dreyfus算法已成为确定情况下的经典算法.而不确定情况下的最短路径问题，大致分为4个方面[11]：研究路段长度随机变化的最短路径；研究不同费用函数的最短路径；研究时间独立情况下的路段长度随机变化的最短路径；研究路段长度为区间范围的最短路径.但以上最短路径分析未考虑城市车辆在实际行驶中对道路选线的不确定因素，为此本文作者在传统Dijkstra算法优化基础上做进一步研究:首先，借助GIS网络分析技术,将城市道路网络转换成有向图，包含节点和链路；其次，将城市道路网络节点和路段上距离或时间阻强(障碍、限速、节点延迟)作为约束条件；再次，考虑道路类型、节点停留时间、限速、车辆行驶方向等条件，对比分析从起点到终点的时间或费用；最后，根据时间成本和距离成本约束因素，分别对无约束条件、障碍路况、限速模式下的最短路线进行了实地验证，并确定最优路线.

1 路径分析模型

1.1 Dijkstra算法

Dijkstra算法是1959年由荷兰计算机科学家Dijkstra提出的图论中求最短路径的常用算法[12]，该算法可求得图中一点到其他任一顶点的最短路径[13].Dijkstra算法将网络节点分成3部分：未标记节点、临时标记节点和永久标记节点.在网络图中，将所有节点初始化为未标记节点，在搜索过程中游历节点和任一路径中相连通的节点为临时标记节点，每次循环都是把从临时标记节点中搜索距起源点路径长度最短的节点作为永久标记节点，直至找到目标节点或者所有的节点都成为永久标记节点后才算法结束.如图1所示，假设节点网络的起源点为节点0，目标点为节点4，求节点0到节点4最短路径的距离(各节点间的长度是假设的).

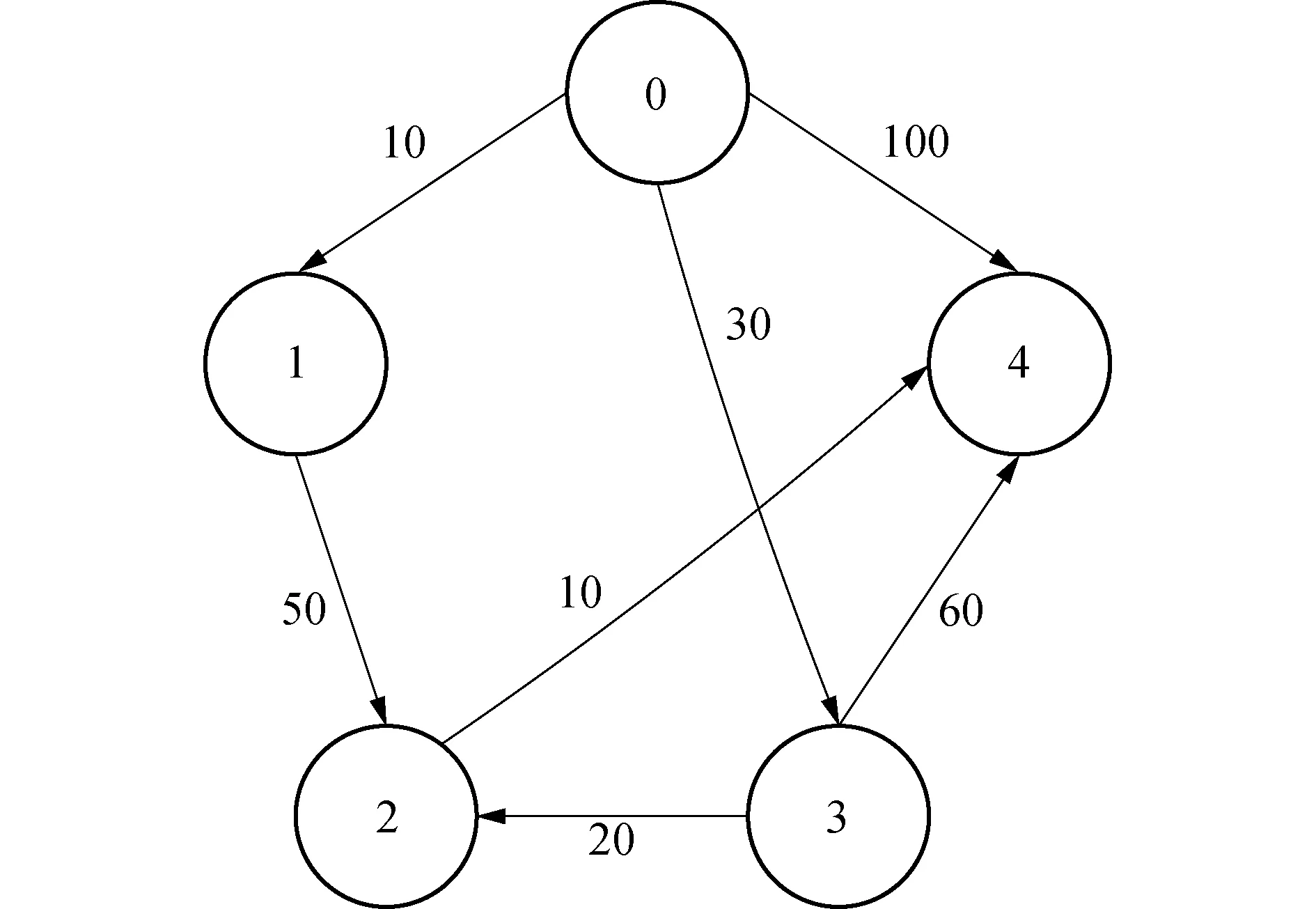
图1 路径的节点网络Fig.1 The meshed network of the route

假设每个节点都有一对标号(wi，pj)，wi是起源点到目标点的最短路径的长度，wj是从起源点s到任意节点j的最短路径长度(从顶点到其本身的最短路径是零路(没有弧的路)，其长度等于零),pj为从起源点s到节点j的最短路径中j点的前一节点.求解从起源点i到目标节点j的最短路径，基本过程如下：

1)初始化.起源点设置为

①若起源点s最短路径长度ws=0，ps为空；

②所有其他节点的路径长度wi=，pi=s；

③标记起源点s.记所有已标记的节点k=s，其他节点设为未标记的.

2)检验从所有已标记的节点k到其直接连接的未标记节点j的距离，并设置

wj=min{wj，wk+dkj}

(1)

式中：wj是未标记节点j的最短路径长度；wk是已标记节点k的最短路径长度；dkj是从节点k到节点j的直接连接距离.

3)选取下一个点.从所有未标记的节点wj中，选取最小的一个标记节点i,即wi=minwj(所有未标记的节点j)，节点i就被选为最短路径中的一点，并设为已标记的点.

4)找到节点i的前一点.从已标记的节点中找到直接连接到节点i的点j′，作为前一点，设置i=j′.

5)标记点i.如果所有节点已标记，则算法求出最短路径(见表1);否则，记k=i，转到步骤2)再继续.

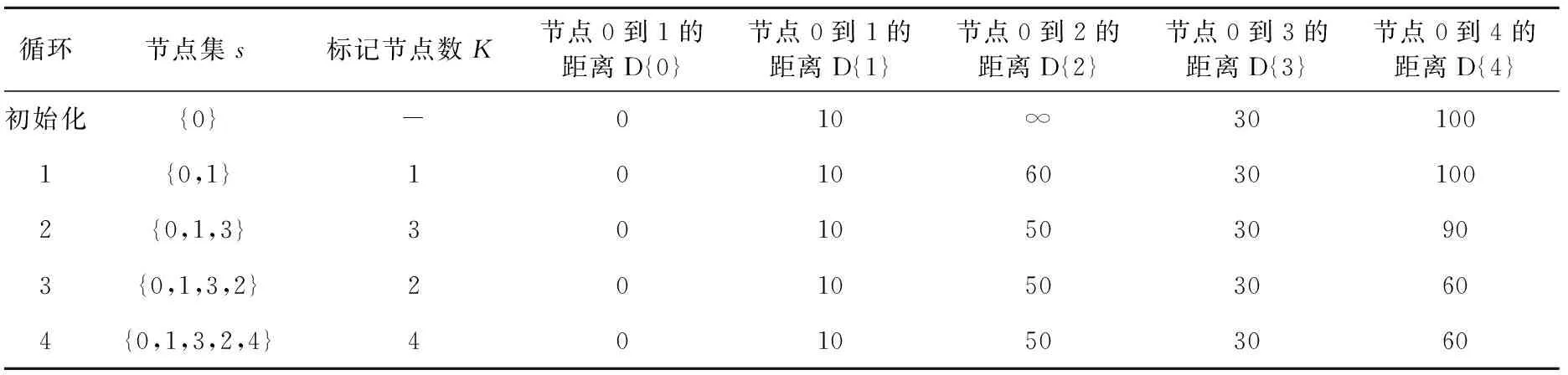
表1 0节点到4节点的最短路径

1.2 算法优化

Dijkstra算法优化思路如下：首先,从起源点s的临时集合NBs(与起源点s直接相连的节点集合)中选择距离最小的邻居节点k作为转接点，同时划归到标识集合S(初始时，为S{s})；然后，对k临时集合与标识集合的差集中节点的值进行更新，从标识集合S中所有节点的临时集合的并集与标识集合的差集(∪NBsS，i∈S)中选择一个路径距离值最小的节点Wk作为下一个转接点，并划归到标识集合S中.重复上述过程，直到所有的节点都被标识过，即|s|=n，算法结束.

设NBi为节点i的临时集合,S为标识集合,wi是从源点s到节点j的最短路径长度,Pi是从s到j的最短路径中j点的前一节点,dij是节点i到节点j的距离.算法过程[14]如下:

1)初始化标识集合S={s},wi=dsi(i∈NBs),否则wi=(i∉NBs)；Pi=s.

2)若k临时集合节点到起源点距离最小dsk=mindsi，则S=S∪{k}，j∈NBs.

3)修改k临时集合节点NBk=S中的wi值,wi=min{wi，wk+dki}；若wi值改变，则Pj=k，j∈NBs-S.

4)选定已标记的临时节点集合NBi-S(i∈S)中的wi最小值，并将其划归到s中,wk=minwi,S=S∪{k}；若|s|=n,节点已标识，则算法终止，否则转到步骤3).

对于节点总数为n的网络图，Dijkstra算法求解最短路径总共需要迭代n-1次，每次迭代都新加一个节点到临时节点集合中，由于第i次迭代时不在临时节点集合中的节点数为n-i.那么，第i次迭代需对n-i个节点进行处理的次数为

(2)

当式(2)中的网络节点数量为n时，路径求解的时间复杂度为O(n2)，即为网络图上从起源点到其余各节点的最短路径求解的时间复杂度.随着节点总数n的增大，其计算效率和存储效率降低.

时间复杂度O(n2)取决于转接点k的临时集合NBs的元素数量，那么优化算法空间复杂度为O(n×p)，其中p为邻接矩阵存储结构N×N下节点对象所占用的空间，是常量.另外，根据网络节点和路段的个数，可以求出节点的平均出度e,即

(3)

式中：m为路段数.

一般在GIS网络关系图中，e∈[1，4]，由于步骤3)、步骤4)都是搜索与Vi(i=l，2，3，…，n)相邻的节点操作，时间复杂度均为O(n×e)；步骤4)的时间复杂度为O(m)，即O(n×e).

1.3 模型构建

选取汉中市主城区道路网络作为研究数据，将高速公路、国道、省道、县道、铁路、主干道、次干道、乡镇道路等矢量要素导入到本地地理数据库.首先，指定参与道路网络矢量要素的拓扑等级,设置容限值(限速、限行)和转弯模型，建立道路弧线段-节点拓扑网络模型；其次，根据道路网络节点-弧线段连通规则，设定费用变量和约束变量，费用变量为路径成本费用[15]，约束变量属性字段为布尔值，即为单行和双行线；最后，设定道路网络中路段的行驶方向和节点延迟.通过网络拓扑规则和关系，建立节点和路段连接的有向网络图，其模型为

(4)

式中：Rw代表道路网络；N代表节点集；R代表路段集合，其元素为有序对〈x,y〉，且表示由节点x到节点y存在一条有向通路；LR代表路段的加权长度，其元素L(x,y)表示有向路段〈x,y〉的加权长度；lxy为节点x到节点y的任一路段长度.

路段的加权长度LR是指根据多目标函数和规划要求，综合各种动态和静态属性约束条件后求解的最优路径[16]，而并非路径的实际距离或者长度.因此，最优路径不仅指一般地理空间意义上的距离最短[17]，还可以引申到时间、费用、线路容量等[18].

1.4 阻强问题

道路网络既有起点、终点、停靠点、路径、路障等，又有费用成本、等级、限制和描述符[19].其中，阻强是网络中的节点或路段因某些突发事件(如交通事故)而不可运行时，原来获得的最优路径需要进行修正，具体步骤如下：

1)修路时，即某个路段不可运行，属于永久性的.当道路在维修时，最优路径的距离也随着维修状态而发生改变.

2)交叉路口出现车祸等情况时，暂时不可通行，即网络中的节点不可运行，延长了车辆行驶时间.

任一路径的综合路阻C采用加权求和法计算[20]，有

(5)

式中：Ci为第i路段的综合路阻；Dij为第i路段中的路阻因素分值；aj为第j路阻因素权重.

任一路段路阻因素分值Dij的计算采用上限测度，计算公式为

Dij=dij/dj，max

(6)

式中：Dij为第i路段j路阻因素分值；dij为路阻因素的实际值；dj，max为第j路阻因素的最大实际值.

2 结果与讨论

2.1 无约束条件下的最优路径

假设汉中站为初始源点，陕西理工大学南校区南门为目标节点，在任意路口可以调头，计算汉中站—陕西理工大学南校区南门的距离和时间最优路径.如图2(a)所示，在车辆行驶速度理想的状态下，从汉中站到陕西理工大学南校区南门的距离最短路线长为4 377.8 m，所用时间成本为10.7 min，而在时间约束模式下的路线距离为4 384.9 m，行驶时长最小为9.7 min，如图2(b)所示.在实际行驶中，路线选择受驾驶员对时间最短和距离最短的偏好影响.

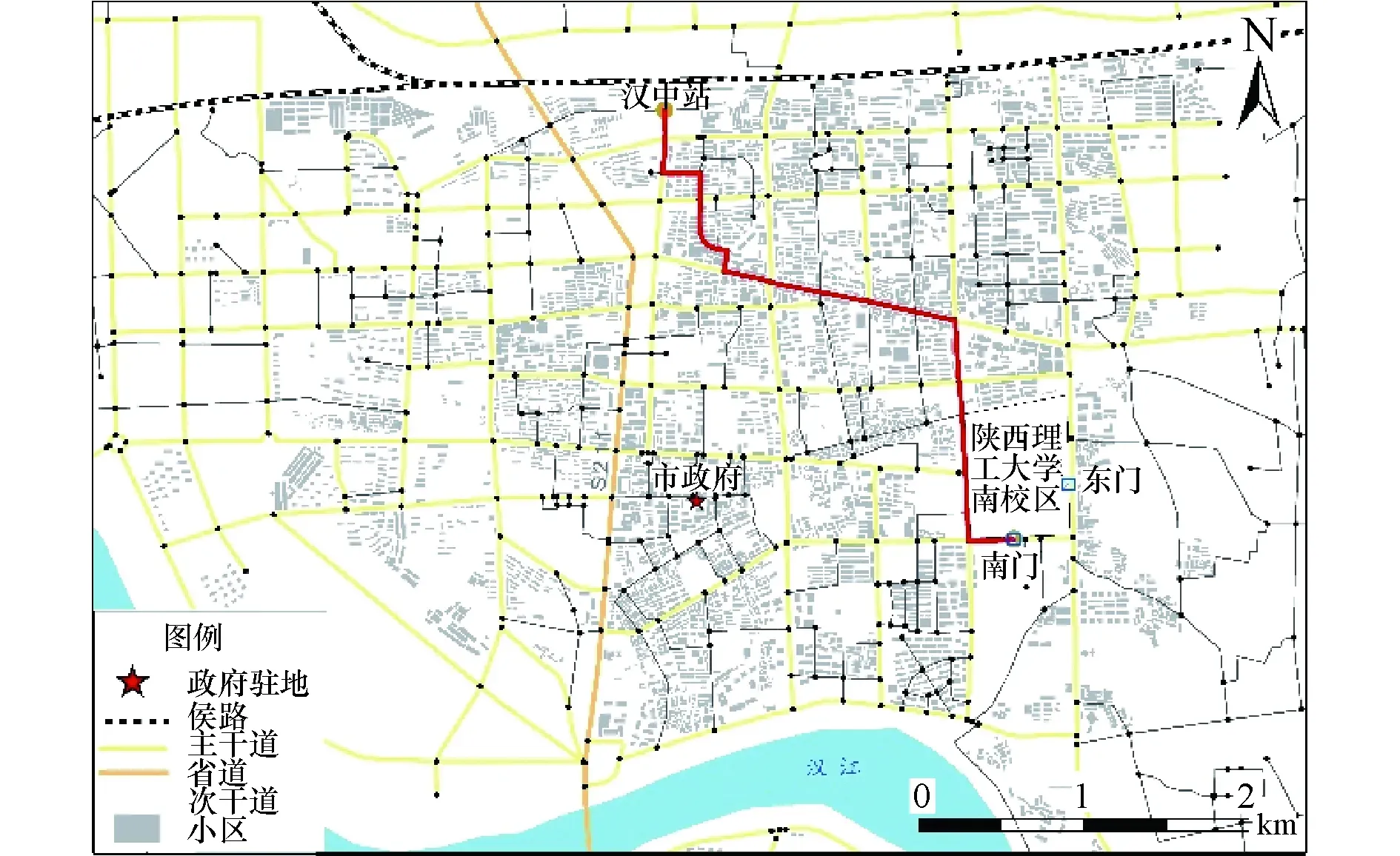
(a)距离最短路径

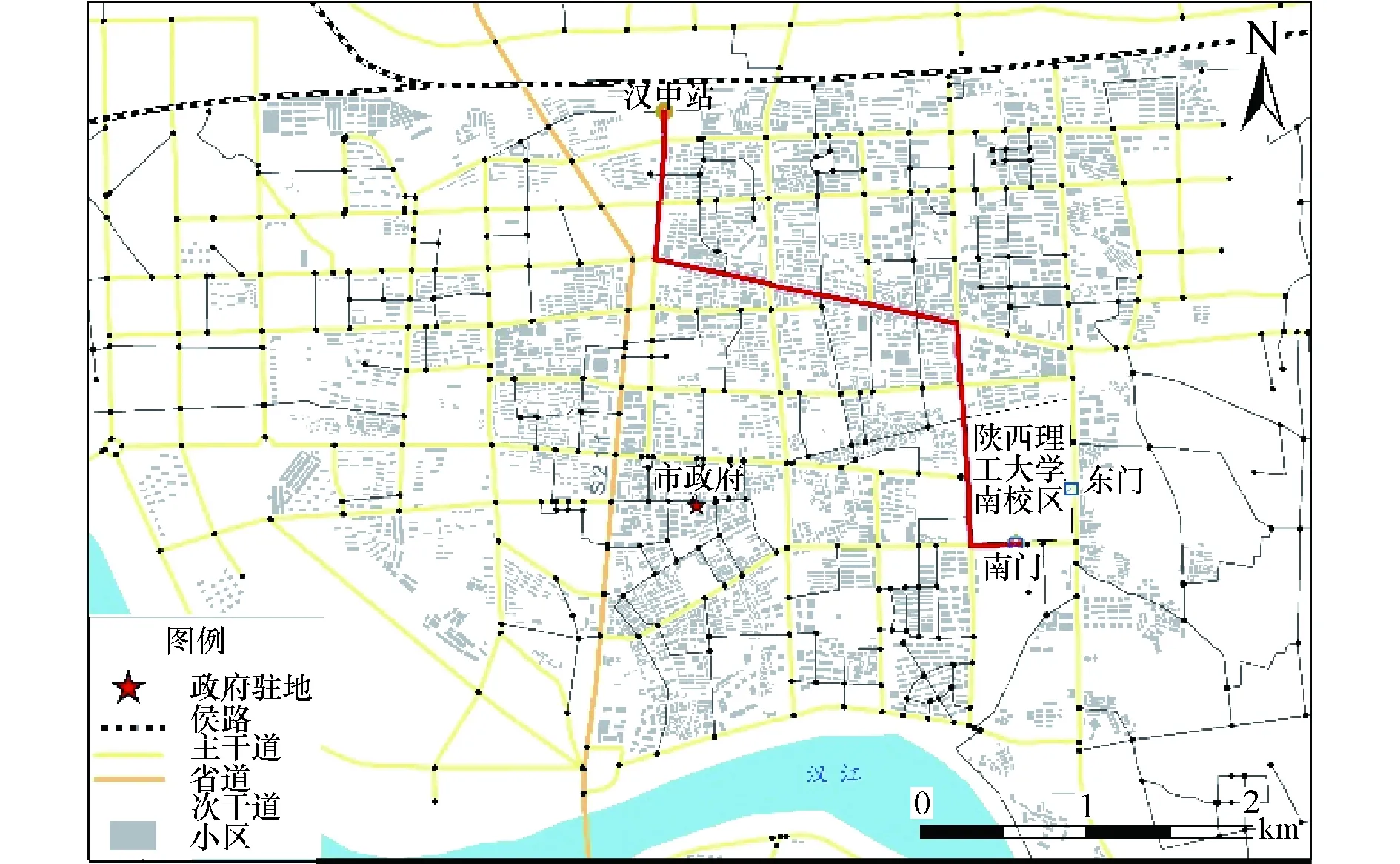
(b)时间最短路径图2 路径选择Fig.2 Route choice

2.2 障碍路况下的最优路径

假设在繁杂路口、事故现场、医院等位置节点车流量大，设置临时障碍点，短时间内车辆禁止通过，计算距离最短和时间最短路径.如图3所示，在障碍路况下，车辆行驶的最短距离为4 610.3 m，时间成本为10.7 min;最短行驶时间为10.2 min，行驶距离为4 630.6 m，二者在时间和距离成本上相差不大.这表明,从汉中站到陕西理工大学南校区南门时，最优路径的选择受行驶距离或行驶时间成本的影响甚微，不起决定性作用，可在时间成本和距离成本模式下自主选择.

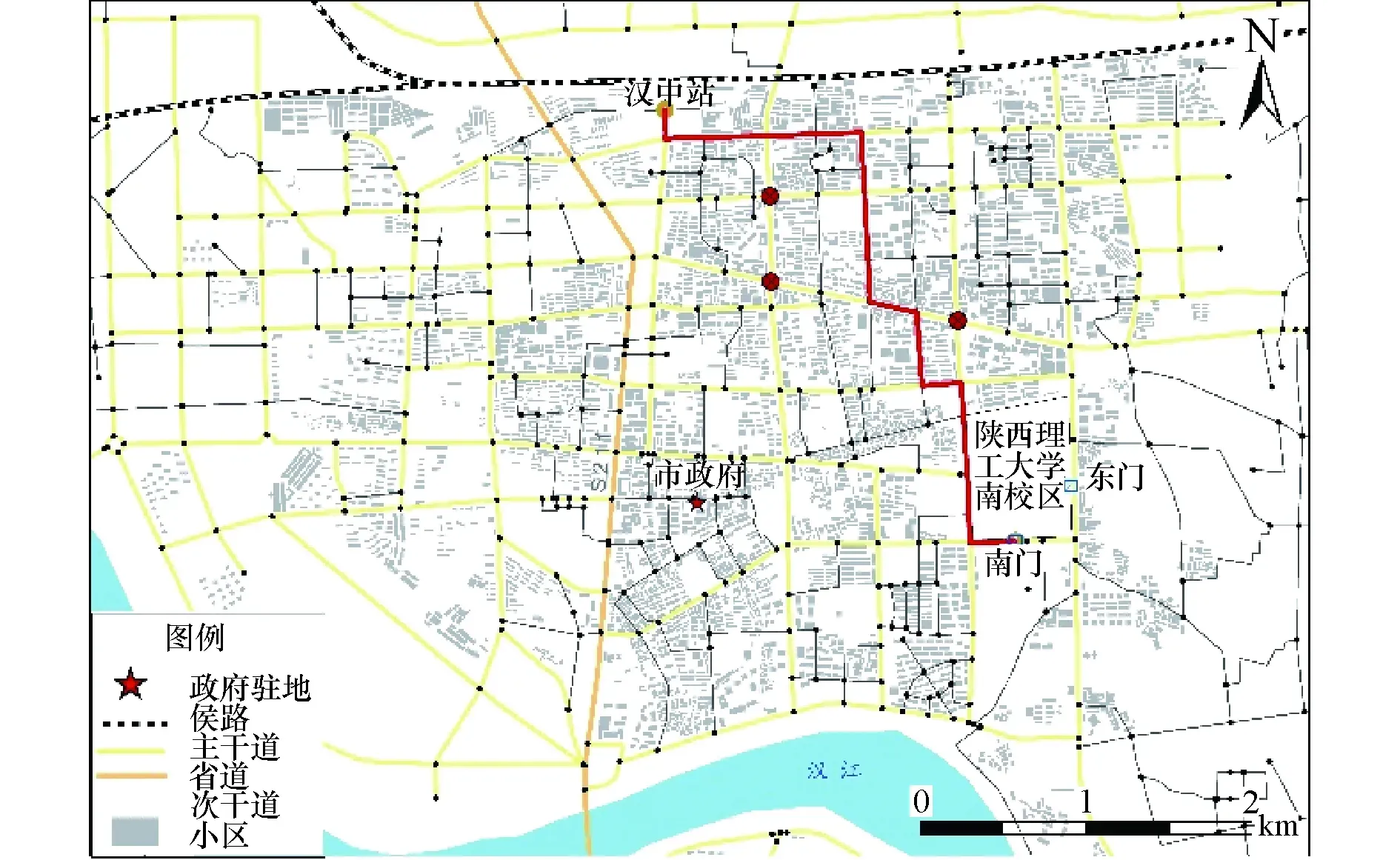
(a)距离最短路径

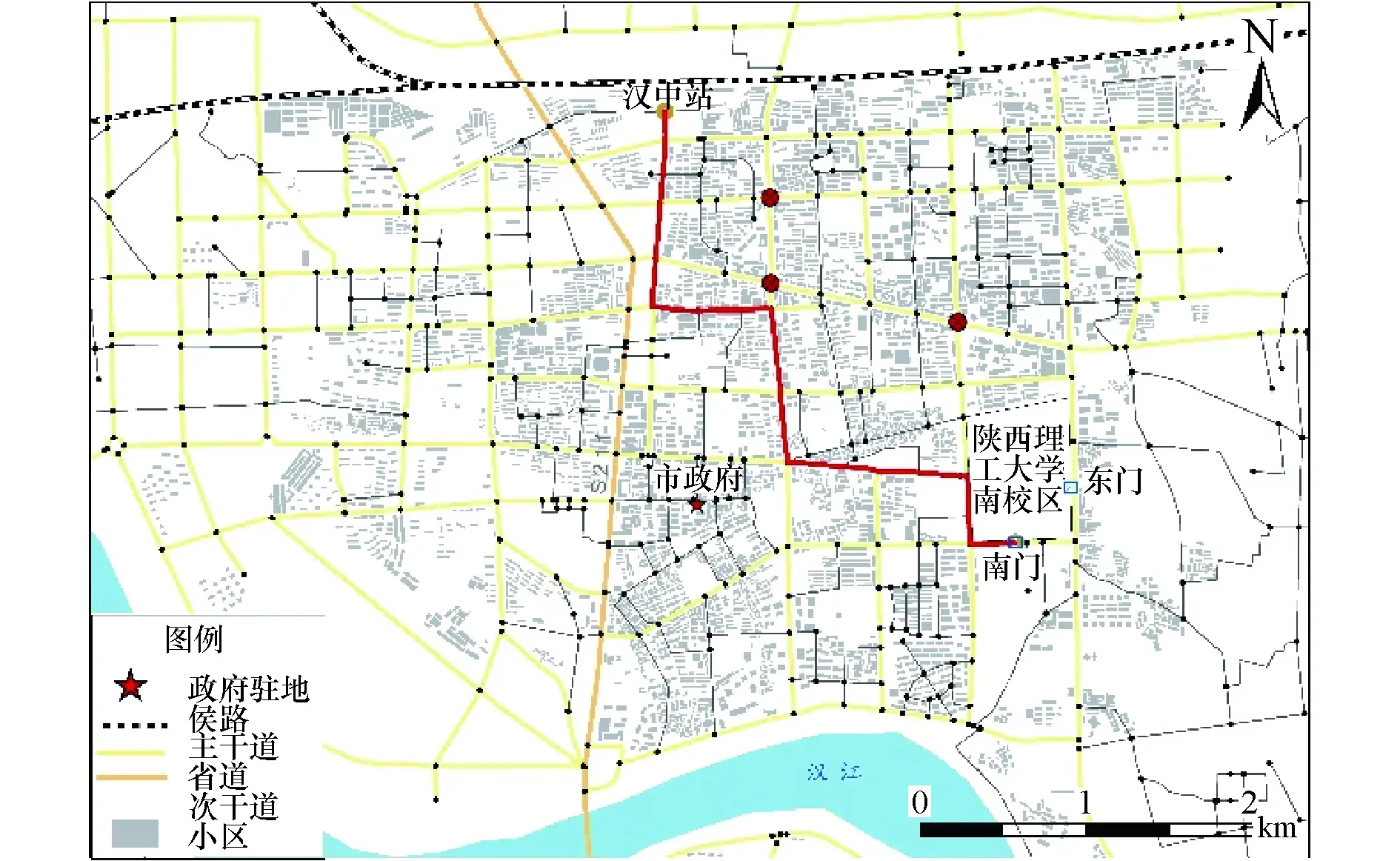
(b)时间最短路径图3 障碍路况下路径选择Fig.3 Route choice under the barrier

2.3 限速限行模式下的最优路径

基于道路网络等级、路段限速模式下，驾驶员在主观意愿上会优先选择省道、国道、城市主干道，其次选择城市次干道、乡镇道路.假设主干道限速30 km/h、次干道限速25 km/h、省道限速35 km/h，计算出在限速模式下的最优路径.在限速模式下，距离最短路径需要行驶4 455.3 m，行驶时间成本为13.2 min(见图4(a))，比无约束模式下的时间最短路径多行驶2.3 min.限速模式下的最短时间为10.5 min，行驶距离为4 739.4 m(见图4(b))，与最短距离路径模式相比，时间成本降低了，距离成本增加了361.5 m.在道路通行能力有限情况下，尤其在上下班高峰期，实际的行驶时间与最优路径的行驶时间存在较大差异.而交通路况在非高峰时段，最优路径与实际行驶时间和距离成本较为接近.

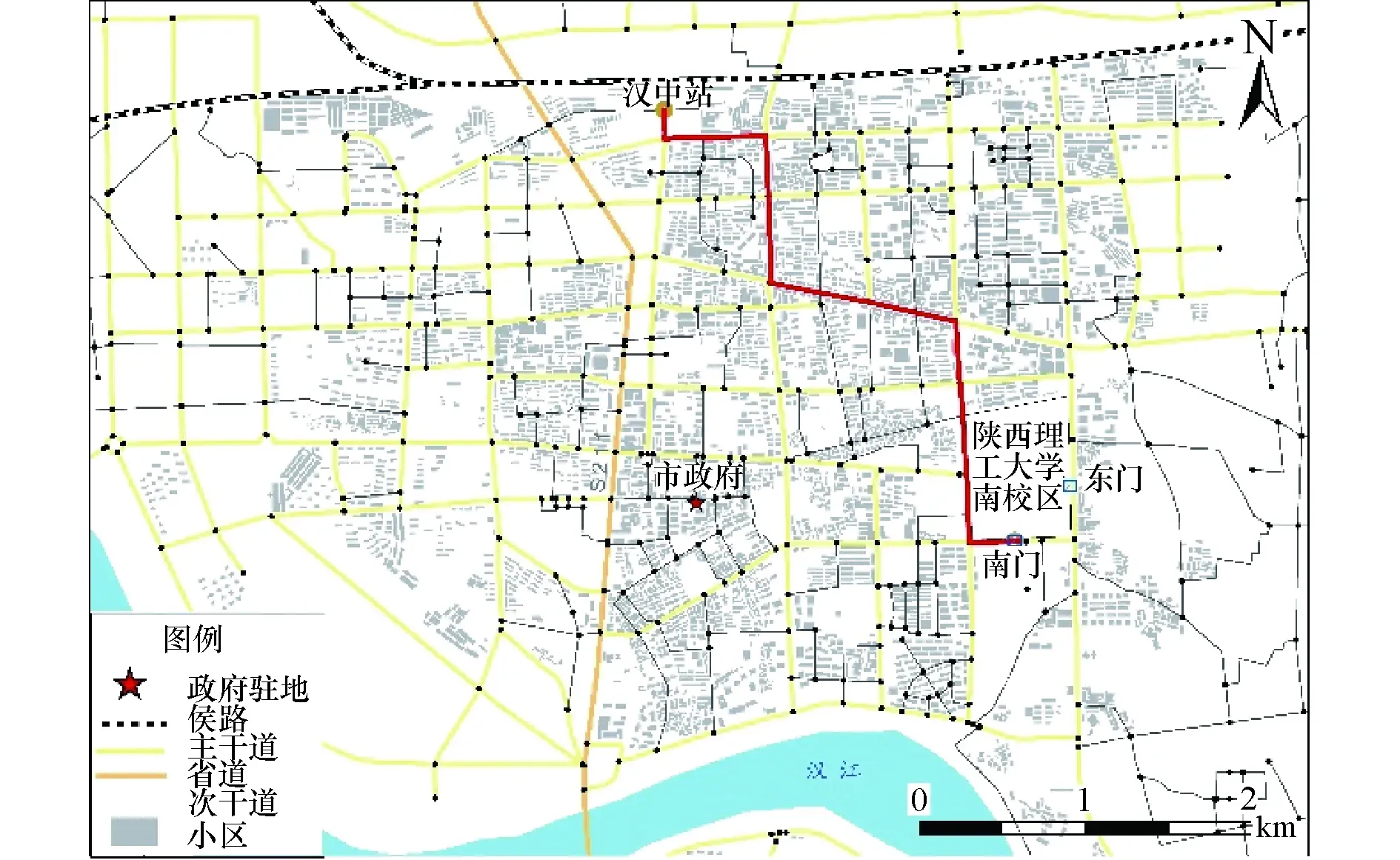
(a)距离最短路径

(b)时间最短路径图4 限速模式下路径选择Fig.4 Route choice under the speed binit mode

优化后的Dijkstra算法和传统Dijkstra算法，在计算路径的运行时间和距离最短时，主要取决于行驶路线的节点数量.时间最短和距离最短路径的求解有不同之处，主要表现在有向图中每条路段上障碍点、行驶方向、限速的设置.假设每个限速路段节点的延时时间为30 s，非限速路段的节点处延时25 s，行驶过程中通过的红绿灯最少，计算出时间最短路径为18.4 min，比限速模式下时间最短路径的时间成本多5.2 min，如图5所示.

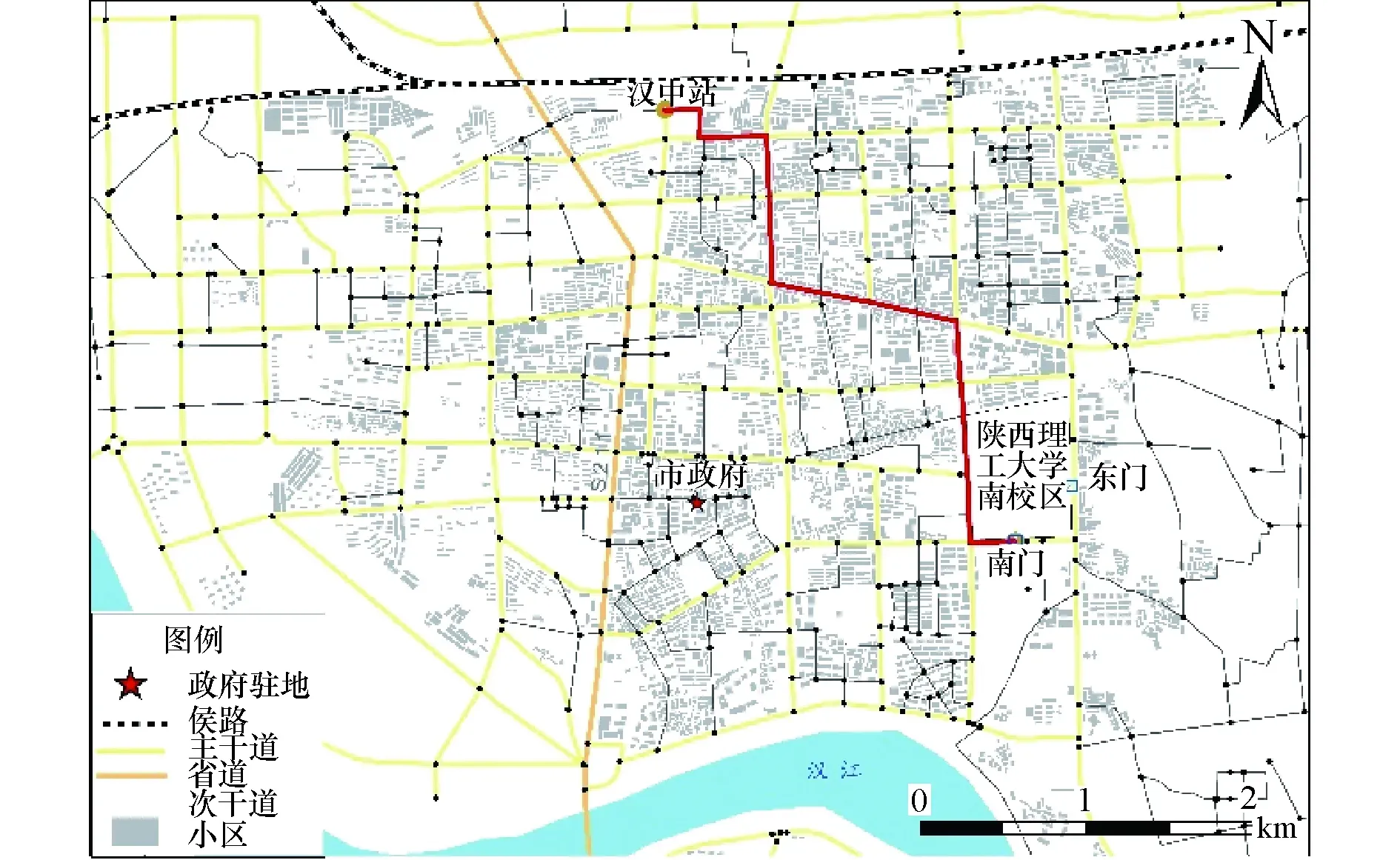
图5 节点延时条件下的距离最短路径Fig.5 The shortest route of distance under the node delay conditions

2.4 选线结果对比

为检验优化路线的行驶理论时长和实际行驶时长(见表2)，与优化路线的行驶时长相比，实际行驶时间用时较长，最小时长差值为1.2 min，最大时长差值2.9 min.在城市道路网络不限速、不限等级的情况下，时间最短路径的行驶距离(线2)比距离最短路径的行驶距离(线1)多行驶了7.4 m，以行驶距离增加和道路等级降低来换取行驶时长最小化.在障碍路况模式下，线4时间行驶时长比线3的实际行驶时长多了1.0 min，行驶中的驾驶员对障碍点和路况不熟悉，实际行驶时长比模型输出的理论行驶时长多用了2.9 min.在限速模式下，线5中城市车辆的行驶时长实际值受限于道路拥堵、通行能力、路况信息等条件，比线6实际行驶时长多了1.2 min，与行驶理论时长多了2.3 min.而在路口节点处延时30 s的情况下，实际行驶距离较为合理，实际行驶时长较大.因此，节点延时、障碍路况、限速限行是影响城市车辆选线的主要因素，最优路径中节点数量对行驶时长和行驶距离起到主导作用.

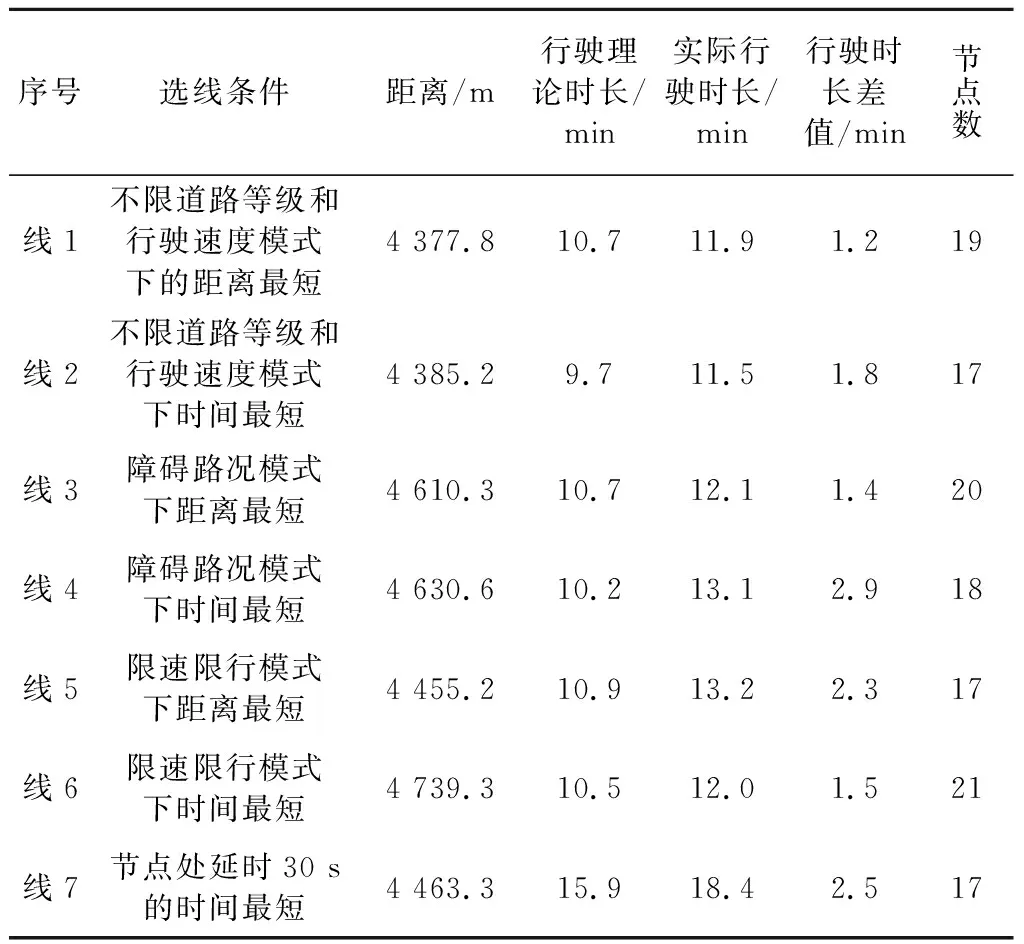
表2 基于Dijkstra算法优化的车辆选线与实际行驶时间对比Tab.2 Comparison of actual driving time and vehicle routing results after the optimization of Dijkstra algorithm

3 结论

1)通过对传统Dijkstra算法的优化，利用GIS网络分析工具，对城市车辆选线进行求解，获得了不同约束条件下的时间和距离最优路径，并给出最短路径长度和行驶时间.在理想情况下，GIS网络分析工具能够精准模拟复杂的道路网络，使模型中的选线结果与实际选线结果较为一致.

2)Dijkstra算法优化可减少路径分析过程中的节点访问时间，降低时间复杂度，缩短已标识节点外的大量节点的计算时长.但是，最优路径的成本仍取决于路径节点数、路段阻强和限速条件.

3)在道路网络中指定起源节点和目标点，分别求出在距离、时间成本的限制下的最优路径.但是针对城市公共交通工具的进出站、路段限行、道路拥堵等路况条件，需要采用相应的路径优化措施.Dijkstra算法优化倾向于选择主干道、无障碍路、次干道，在驾驶员主观和客观因素(如司机态度、偶然事件、拥堵路段、节点访问次序、交通临时管制)方面还有待进一步研究.