基于双折减策略的边坡稳定性分析

成子桥，李建宇，吴顺川，熊良锋

(1.中电建路桥集团有限公司，北京 100044；2.北京科技大学 土木与资源工程学院，北京 100083)

边坡稳定性评价的核心主要在于求解边坡安全系数及其对应的临界滑面.目前，较为常用的分析方法主要包括极限分析法，极限平衡法及数值分析方法.极限分析属于边坡稳定问题的严格解答[1]，而极限平衡法是一类求解边坡稳定问题近似解的方法[2]，二者结果通常较接近[3].数值分析方法通过强度折减的方式不断降低边坡岩土体抗剪强度参数直至达到极限平衡状态为止[4-5]，根据弹塑性理论计算结果得到滑动破坏面，同时得到边坡的强度储备安全系数.通常情况下，认为黏聚力和内摩擦系数随损伤的演化规律相同，故对二者统一折减，由此确定边坡安全系数.

在岩土体变形破坏过程中，黏聚力和内摩擦系数随损伤的演化趋势不一致[6-7]，因此传统强度折减法可能与实际情况相悖.为此，文献[8]建议黏聚力和内摩擦系数分别采用不同的折减系数.双折减系数的引入，使传统的安全系数定义和强度折减策略已难以满足要求，因此许多学者针对这两方面内容展开了细致地研究.文献[8-11]根据极限平衡法基本原理论证了双折减方法的合理性，并认为黏聚力折减系数应大于内摩擦系数折减系数，且假定安全系数为二者的算术平均值.在此基础上，文献[12]将双折减方法推广至边坡数值分析.基于边坡临界强度线的假设，文献[13-15]分别提出了不同的最短折减路径，并建立了相应的安全系数定义.文献[16]根据极限分析理论认为后者定义更为合理.文献[17-18]主要探讨了双折减方法和传统强度折减法的联系，并提出边坡安全系数应采用极限平衡法的定义方式.考虑到岩土材料的应力应变关系，文献[19-21]提出了基于应变软化规律的强度折减路径，文献[22]将该方法应用于Heok-Brown本构模型.然而，上述研究通常仅考虑个别的安全系数定义，鲜有系统地比较分析.

本文作者将通过构建一套逐步折减方案，开展相关边坡双折减数值试验，以探讨不同安全系数定义的适用性，为双折减方法的应用提供理论支撑.

1 双折减方法概述

由于采用两个不同的折减系数，双折减方法可表征岩土体的不同软化路径，从而揭示边坡的真实劣化过程.为准确获取边坡稳定性信息，该方法需考虑无数种强度折减路径，其计算量将尤其繁重.因此，双折减方法关键在于合理选用安全系数定义和强度折减路径.

安全系数是边坡稳定分析的主要定量指标.双折减方法中黏聚力和内摩擦系数折减系数(分别记为Fc、Ff)通常不一致，因而安全系数定义显得尤为重要.目前安全系数定义主要包括下列3类方案：

1)数学平均值方案

该方案将安全系数定义为双折减系数的数学平均值[8-13]

算术平均值F=(Fc+Ff)/2

(1)

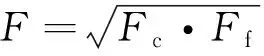
(2)

调和平均值F=2/(1/Fc+1/Ff)

(3)

(4)

2)强度折减路径方案

该方案将强度折减路径长度与传统折减路径长度(Fc=Ff)的比值视为安全系数[14-16]

(5)

(6)

3)极限平衡法方案

该方案将抗滑力与下滑力的比值定义为边坡安全系数，即

σtanφ/Ff)dl

(7)

对于数值模型，若滑面由m个单元组成，则式(7)可表示为[17-22]

σitanφ/Ff)li

(8)

其中：c、φ分别为边坡介质的黏聚力和内摩擦角；σi和li为第i个单元垂直滑面的正应力和沿滑面长度.采用该方案时应准确定义滑面位置，以获取滑面上各单元的正应力及长度，由此求解安全系数.

双折减方法将黏聚力和内摩擦系数折减系数间的数学关系定义为强度折减路径，即假定Ff=g(Fc).在此基础上，不断折减黏聚力和内摩擦系数，直至边坡处于临界平衡状态，由此得到双折减系数.根据数学关系的不同，强度折减路径主要包括下列3种：1) 假定Fc/Ff为一定值[8-12]；2) 基于应变硬化软化模型，确定强度折减路径[19-22].在应变硬化软化模型中，黏聚力和内摩擦系数表示为塑性内变量的函数，由此可确定双折减系数间的数学关系；3) 假定边坡介质的临界力学参数关系已知，按路径最短原则确定强度折减路径[14-16].

方案1)主要基于经验判别；方案2)中黏聚力和内摩擦系数随塑性内变量的演化规律，往往依赖于室内试验的特定应力路径，该特定路径与边坡介质的软化路径通常并不一致；而方案3)考虑强度折减的最短路径.理论上讲，双折减方法需全面考虑各种不同的强度折减路径.在分析此类非线性问题时，计算应尽可能模拟其真实的物理过程[23]，而最短路径即为最可能的边坡介质劣化方式[14-15].因此，方案3)可作为双折减方法的强度折减策略.该方案认为，边坡处于临界平衡状态时，其介质强度参数存在唯一确定的数学关系，相应的关系曲线称为边坡临界强度线，见图1.边坡临界强度线表示边坡临界状态时岩土体强度参数(即折减后的黏聚力c和内摩擦系数f)的组合，故强度折减路径即为边坡岩土体强度参数由其初始值至边坡临界强度线上某点(临界值，如图1中点Pi、Bi或Di)的路径.如图1，边坡岩土体强度初始值由P0表示，边坡临界强度线由粗实线表示(其中，点Ai和Ci表示强度折减中间过程).因而，P0P1可表示方案1)的折减路径，P0P2是传统强度折减法的折减路径，而P0P3即为一种最短折减路径[13].

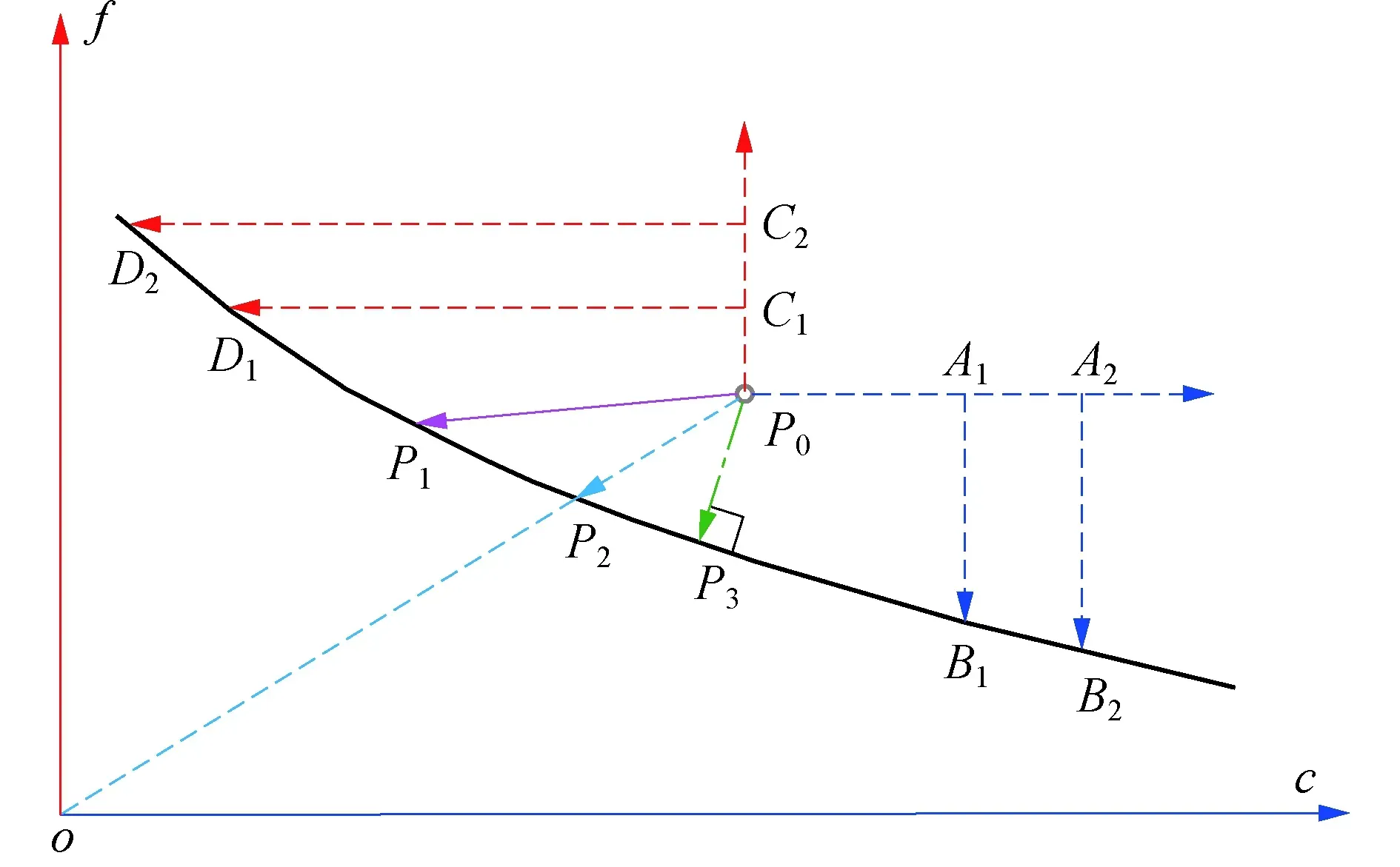
图1 边坡临界强度线Fig.1 Curve of critical strength components for a simple slope

2 双折减数值试验

2.1 边坡概况

考虑一高度H=10 m的均匀边坡，坡角β=45°，岩土体重度γ=20 kN/m3，黏聚力c=12.38 kPa，内摩擦角φ=20°，抗拉强度为0.根据极限分析[3]，该边坡安全系数为1.边坡稳定性分析采用关联流动法则(即剪胀角等于内摩擦角)，以便于和极限分析比较.岩土体弹性参数对边坡稳定性影响很小[5]，因而本文选用经典参数值，即弹性模量E=14.0 MPa、泊松比υ=0.30.参考文献[4]，构建边坡平面应变数值模型(图2)，其包括2 800个单元；数值计算采用FLAC3D 5.01软件，临界滑面根据最大剪应变率云图[24]计算得到，并结合速度矢量[4-5, 24]进行判别，再根据回归分析[25]得到.

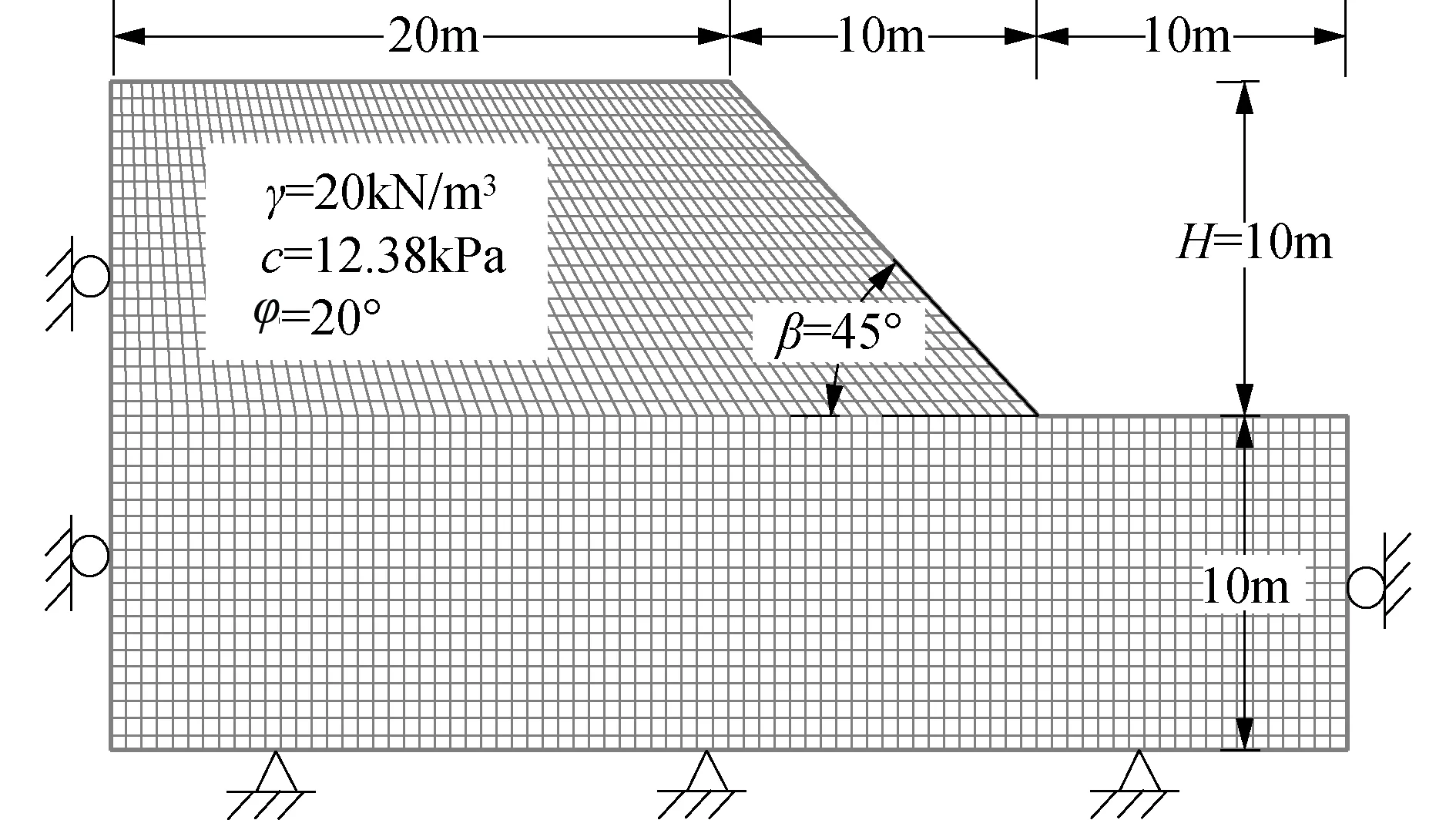
图2 边坡数值模型Fig.2 Numerical model of a simple slope

2.2 双折减方案

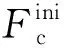
(9)

2.3 试验结果分析

图3为数值试验的双折减系数及其安全系数.由于该方案需根据临界滑面确定，其余方案仅与双折减系数有关，故此处仅计算极限平衡法方案的安全系数值.随着黏聚力折减系数的增加，内摩擦系数折减系数保持减小且降幅亦逐渐减小，而安全系数先减小后增加，因此安全系数存在最小值.显然，该最小值小于传统强度折减法计算计算结果.

图4为不同折减路径下的边坡临界滑面.其中，

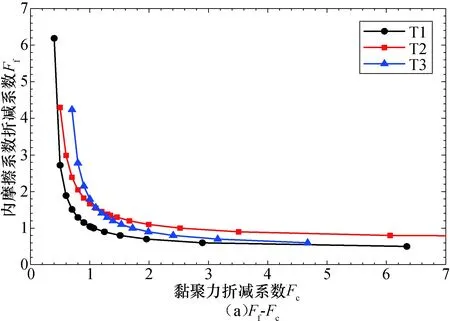
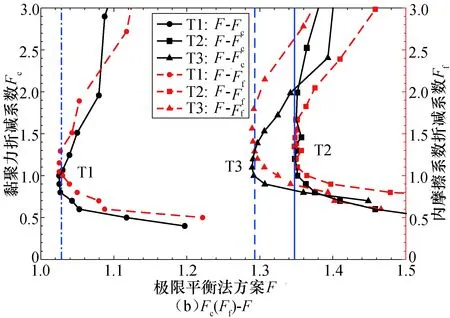
图3 折减系数与安全系数间的关系曲线

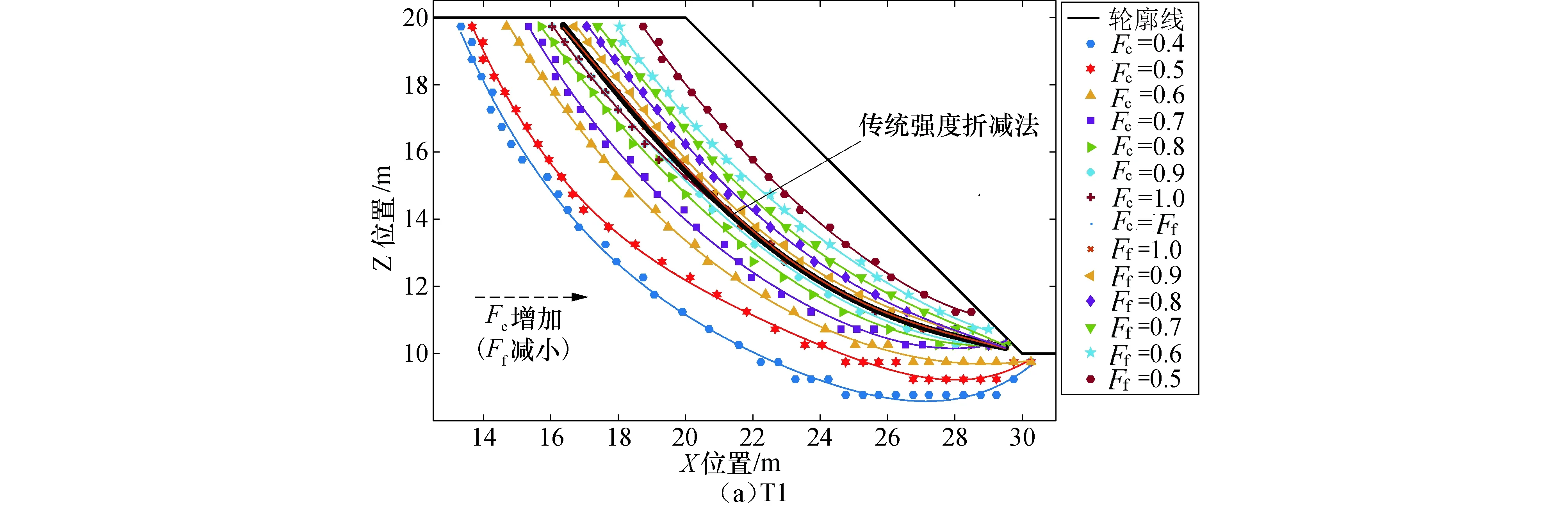
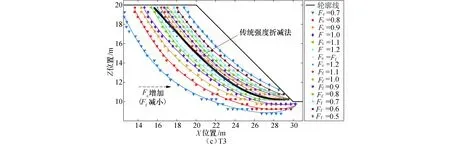
图4 不同折减路径下的边坡临界滑面Fig.4 Critical slip surfaces under different reduction paths

各数据点表示组成临界滑面的单元中心位置，拟合曲线代表各组数据点回归分析的临界滑面.当Fc逐渐减小，即临界黏聚力增加时，边坡临界滑面逐渐向坡体内部转移；当Ff逐渐减小，即临界内摩擦系数增加时，边坡临界滑面逐渐向坡体表面转移.不难看出，临界滑面对黏聚力的敏感性高于内摩擦系数，因而边坡处治可优先考虑提高岩土体的黏聚力，如注浆等岩土改性措施.对比图3、4，3组试验结果规律基本一致.但在T2试验组中，当安全系数趋近于最小值时，其数值波动明显，其原因可能是相邻各组滑面较接近，导致计算时存在误差.对此，可建立更精细的数值模型，并优化临界滑面确定方法.

3 边坡临界强度线

图5绘制了折减后的黏聚力和内摩擦系数，其即为数值计算得到的边坡临界强度线.可以发现，上述3组试验的边坡临界强度线基本重合.因此，对于不同的初始强度参数，均存在唯一确定的边坡临界强度线.对于特定边坡，临界内摩擦系数随临界黏聚力增大而减小，且降幅逐渐减小.

当边坡结构参数(如坡角、坡高等)和岩土体重度发生变化时，边坡临界强度线将随之改变.基于对数螺旋线破坏面假定，均质边坡稳定性的上极限解答，采用无量纲的稳定数表示[3]

Ns=γH/c

(10)

图5 数值试验计算的边坡临界强度线Fig.5 Curve of critical strength components computed by numerical tests

对于上述边坡数值模型，根据式(10)可计算不同临界内摩擦角所对应的临界黏聚力大小，从而得到边坡临界强度线(ccri,fcri).此即为极限分析求解的边坡临界强度线(图5)，其与数值计算结果非常接近.因此，上述逐步折减路径可作为计算边坡临界强度线的一种有效途径.当边坡形态简单时，极限分析可计算出精确的边坡临界强度线；但对于形态复杂的自然边坡或多级开挖边坡，目前多采用数值方法.但当临界黏聚力较小时，两者存在一定差异；此时边坡失稳表现为浅层滑移，滑面距离边坡表面很近，故粗糙数值模型将引起较大误差.

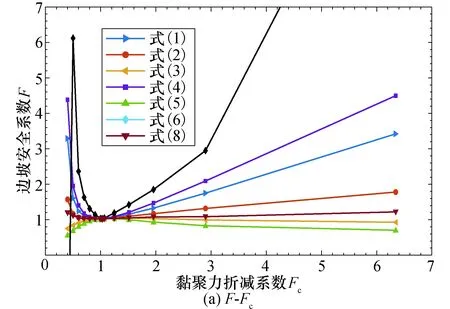
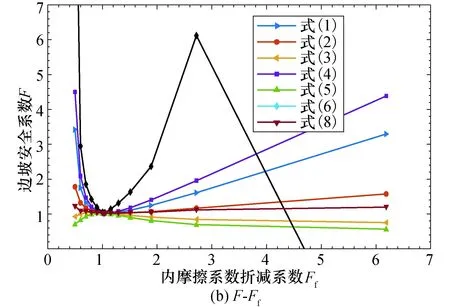
图6 三种方案定义的边坡安全系数Fig.6 Factors of safety defined by three different schemes

综上，安全系数与双折减系数间的关系可用数学平均值、强度折减路径和极限平衡法等方案描述.鉴于3组试验结果基本一致，此处仅绘制T1试验组计算结果，如图6所示.当Fc较小时，式(6)定义的安全系数存在负值，该负值点所对应的双折减系数分别为Fc=0.4和Ff=6.188；而且当Fc较大时，其值急剧增加，因而式(6)并不适用.式(3)和式(5)定义的安全系数表现为凸函数形态，故此二者也不适用.因此，强度折减路径方案均不能合理地描述边坡安全系数.数学平均值方案描述的安全系数大小依次为：式(4)≥式(1)≥式(2)，即均方根平均值≥算术平均值≥几何平均值.随折减系数的变化，该方案定义的安全系数变化也较为显著.此外，极限平衡法方案考虑了滑面正应力的影响，可较好地描述下滑力和抗滑力间的关系，故其定义更为合理.如图6所示，极限平衡法方案定义的安全系数变化较为平缓，且利于和现有规范等比较，因此极限平衡法方案可作为边坡安全系数的定义.

尽管各方案描述的安全系数略有差异，但其极值均位于Fc=Ff附近，且与传统强度折减法的计算结果较为接近.如图4所示，当趋近于Fc=Ff时，不同折减路径下的临界滑面非常接近，且与传统强度折减法结果近乎重合，故双折减方法并无明显优势.因此，建议工程边坡分析采用传统强度折减法.

4 结论

本文系统整理了双折减方法关于边坡安全系数和强度折减路径等方面的研究，并提出一种逐步的强度折减路径，以使边坡处于不同的临界平衡状态.基于简单边坡模型，开展了3组不同初始强度值的双折减数值试验，以探讨各安全系数定义的合理性，主要结论如下：

1)针对简单均质边坡的双折减数值试验，对于不同的初始强度值，其强度折减系数、边坡临界滑面和安全系数的演化规律基本相同，即：随黏聚力折减系数的增加，内摩擦系数折减系数逐渐减小，同时边坡临界滑面位置逐渐由坡体深部向表层转移；而且，边坡临界强度线与初始强度值无关，随临界黏聚力值的增加，临界内摩擦系数值表现出单调递减的趋势.

2)由于定义方案的不同，边坡安全系数的演化规律存在较大差异.考虑到实际工程应用，建议采用极限平衡法方案定义双折减方法的边坡安全系数，以利于和现有规范等比较.采用极限平衡法方案时，边坡安全系数随黏聚力折减系数的演化规律表现为先减小后增加.因而，边坡安全系数存在最小值，其略小于传统强度折减法结果，即基于双折减策略的稳定性分析是合理的.

应注意到，当安全系数趋近于最小值时，边坡临界滑面几乎与传统强度折减法结果重合，且两者安全系数值差异也较小；故与传统强度折减法比较，双折减方法并无明显优势.此外，采用逐步折减路径确定边坡安全系数最小值时，需开展尤其繁杂的数值计算，不利于实际应用.鉴于边坡临界强度线的唯一性，后续研究将考虑结合其建立简单的强度折减策略，以促进双折减方法的实际应用.