基于自由落体的落石冲击土层的理论及LS-DYNA模拟研究

王 星，周天跃，师江涛,2，夏永旭

(1. 长安大学 公路学院，西安 710064； 2. 陕西交通建设集团，西安 710086)

滚石灾害已经成为目前中国的3大地质灾害问题之一，尤其是雨季时隧道洞口处的滚石灾害情况更为严峻.各种滚石防护结构便应需而设，而防护结构设计的核心即是要准确解析并计算出滚石的冲击力.

国内外学者针对滚石冲击力的计算做出了大量的研究：其中传统的Hertz接触理论及Thornton弹塑性理论被广泛引用[1-2].文献[3]深入分析了物体间在静态接触、滑动、滚动、冲击等作用下的力学响应规律，并给出了相应的计算公式.文献[4]通过采用室内试验的方法，得出了滚石冲击力的半经验半理论算法.文献[5]以室内试验及动量定理为基础，给出了一种滚石冲击力的半理论半经验算法.文献[6]从现场测试的角度出发，获得了滚石冲击力及冲击深度的量纲为1的计算表达式.文献[7]研究了滚石直接冲击混凝土板时的力学响应情况.文献[8]对滚石冲击力进行了研究，并得出了滚石冲击力呈现出脉冲式变化规律的结论.文献[9]同样证明了滚石冲击过程属于一种脉冲式的碰撞过程.文献[10]以理论计算为手段，分别推导出了滚石冲击力的空腔膨胀算法以及能量守恒算法.文献[11]采用实验及动量定理的方法，归纳出了滚石冲击力的计算方法.文献[12]同样在动量定理的基础上总结出了滚石冲击力计算方法.文献[13]研究了滚石冲击荷载下垫层材料的动力响应情况.文献[14]分析了滚石冲击柔性防护网的力学响应规律.文献[15]结合理论算法推导出了滚石冲击防护结构垫层的冲击力.

针对滚石冲击力，国内外学者研究成果较多，意义深远.然而目前国内的相关设计规范及其他滚石冲击力的算法，其所得结果多为滚石的平均冲击力，同时日本、瑞士学者所给出的经典算法均是基于试验所得出的半理论半经验算法，且算式中各字母变量的意义尚不十分明确.

为此，本文作者首先基于滚石冲击力脉冲式的变化特点，推导出滚石最大冲击力的脉冲式算法；其次再考虑滚石冲击垫层土体的弹塑性特点，得出滚石最大冲击力的弹塑性算法；再次通过采用LS-DYNA软件模拟分析了滚石的冲击力及侵彻深度随时间的变化规律，并归纳出滚动冲击力的LS-DYNA算法.最终将所获得的3种算法与已有算法进行对比分析，以期为滚石防护设计提供参考.

1 滚石冲击力的脉冲算法

文献[11]提出了一种滚石冲击力的计算方法，定义为关宝树算法，其冲击力P及冲击时间tc的表达式分别为

(1)

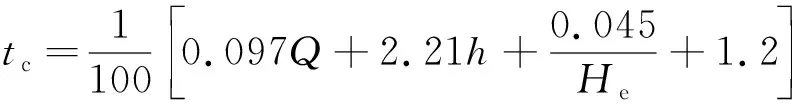
(2)

式中：m为滚石的质量；a为滚石冲击加速度；Q为滚石的重量；g为重力加速度；h为垫层材料的厚度；He为滚石的下落高度.

从而有滚石冲击过程中的平均冲击力Pa为

(3)

由于Pa产生的冲量与实际冲击力P(t)产生的总冲量It相等，则有

(4)

式中：2t0为滚石冲击时间.

滚石冲击过程属于一种脉冲式行为，且冲击力随时间基本呈现出近似正弦变化的趋势[8-10,16]，故考虑P(t)近似满足图1中的正弦变化规律.

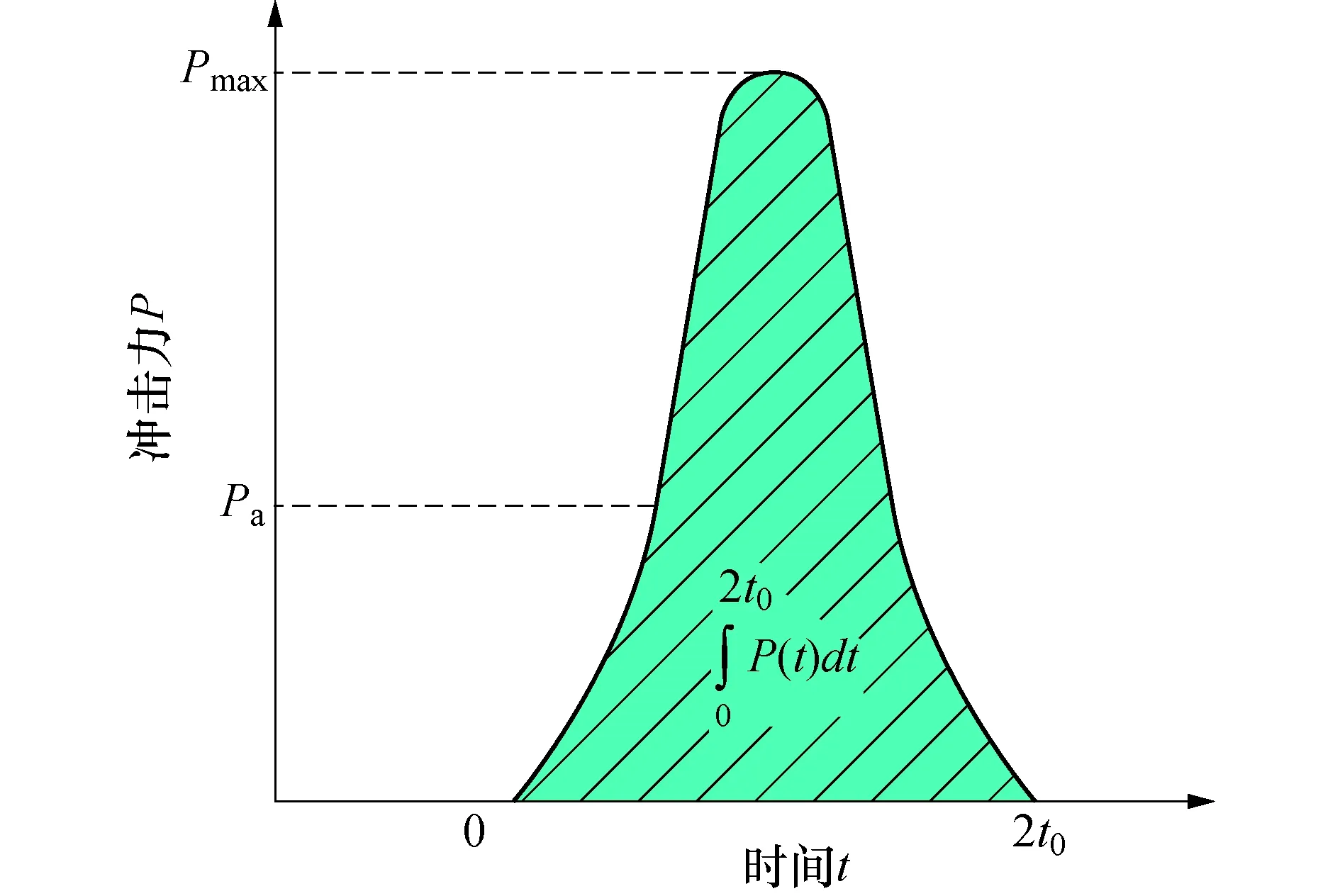
图1 滚石冲击力的变化曲线Fig.1 Variation curve of rockfall impact force

则有滚石实际冲击力P(t)与滚石最大冲击力Pmax之间的关系为

P(t)=Pmaxsin(ω0t)

(5)

根据正弦曲线的性质可得

(6)

式中：T为周期；ω0为角速度.

联立式(4)～(6)可得

(7)

联立式(3)及式(7)，便可求出滚石的最大冲击力Pmax为

(8)

考虑到滚石在冲击垫层土体后会产生一定的回弹，假定滚石的初始速度为v初，反弹的速度为v弹，v初与v弹的方向相反，则有恢复系数κ为

κ=v弹/v初

(9)

根据动量定理，则有考虑恢复系数影响后，对滚石最大冲击力Pmax进行修正的滚石冲击力P修的表达式为

P修t=mv初-(-mv弹)

(10)

联立式(9)～(10)，可以得出

P修t=(1+κ)mv初=(1+κ)Pmaxt

(11)

从而有

P修=(1+κ)Pmax

(12)

考虑恢复系数κ的影响，联立式(8)及式(12)，则可得出滚石冲击力的脉冲算法的表达式，定义为脉冲算法

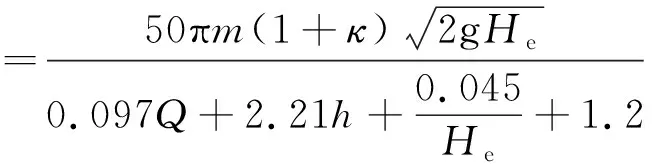
(13)

参数κ可参考文献[17]的实验结果进行取值.

进而求取滚石侵彻深度的理论计算值.假定v(t)为随冲击时间变化的动态滚石冲击速度，则结合牛顿第二定律有

(14)

联立式(5)～(6)、(14)，则有

(15)

对式(15)进行积分后，则有

(16)

(17)

式中：C为常数.

此处存在边界条件t=2t0,v=0，则有

(18)

从而可得出滚石的冲击深度为

(19)

对式(19)进行积分后，则有

(20)

联立式(2)、(13)、(20)，可得

(21)

2 滚石冲击力的弹塑性算法

滚石在冲击下部垫层土体后，最先与滚石接触的正下方土体区域将经历：接触-弹性变形-弹性变形的临界状态-塑性变形，而距离滚石较远的区域则一直保持着弹性变形的状态.在冲击行为发生后，滚石与垫层土体之间将会形成球冠接触面，为了对滚石冲击力进行计算，需通过转换为滚石与垫层土体之间的接触面积大小进行考虑并计算，最终形成图2所示的接触面积的区域划分.图2中，滚石与垫层土体之间形成接触半径为fp的塑性区，而弹性接触面积外缘的半径为fr.

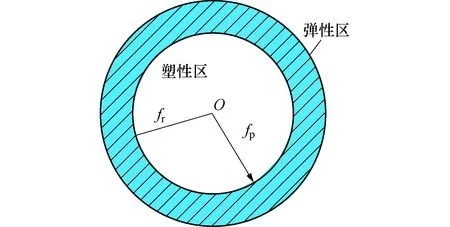
图2 垫层的弹塑性区域分布Fig. 2Regional distribution of elastoplasticity of cushion

滚石球体冲击垫层土体时的弹性接触压力Pe与变形量Se之间的关系式为

(22)

式中：Ra为等效半径；Ea为等效弹性模量.

Ra与Ea计算方式为

(23)

式中：υ1、υ2分别为滚石、垫层土体的泊松比；E1、E2分别为滚石、垫层土体的弹性模量；R1、R2分别为滚石、垫层土体的半径.

滚石冲击垫层土体后会形成一个球冠接触面，其接触面积Ac为

Ac=πf2=πR1S

(24)

式中：f为滚石的接触半径；S为对应于接触半径f下的侵彻深度.

从而有

f2=R1S

(25)

土体在弹性变形阶段的极限屈服应力py及对应的接触半径fy之间满足关系式[18]

(26)

py与屈服应力系数λ、材料屈服强度χM之间的关系，以及λ与υ2之间的关系为[19]

(27)

联立式(25)～(27)，便可以求出滚石的弹性极限冲击深度Sel为

(28)

联立式(22)及式(28)，即可算出滚石的极限弹性冲击力Pel为

(29)

结合图2可得出相应的力学平衡关系式为

(30)

式中：fp为土体垫层的塑性区半径.

从而弹塑性冲击条件下的力学平衡关系式为

(31)

式中：fmax为滚石冲击过程中的最大接触半径；fr为弹性接触半径；Pep为弹塑性冲击力.

联立式(21)、(25)及式(31)便可得出滚石冲击力的弹塑性算法的表达式，定义为弹塑性算法

Pep=Pel+πpyR1

(32)

3 LS-DYNA动态数值模拟

采用LS-DYNA软件模拟滚石冲击垫层土体的动态过程，并选取典型计算工况进行呈现：垫层的材料为砂土，尺寸为5 m(长)×5 m(宽)×1 m(高)，滚石半径为0.5 m，冲击速度为20 m/s.滚石与垫层土体间设置为“面-面接触”，垫层土体中心1.5 m×1.5 m的区域进行了网格加密.垫层土体的下底面设置了3个方向的全约束，滚石的冲击时间设置为0.06 s，计算步设置为200步，此次计算时间约为46 min.材料参数具体见表1.

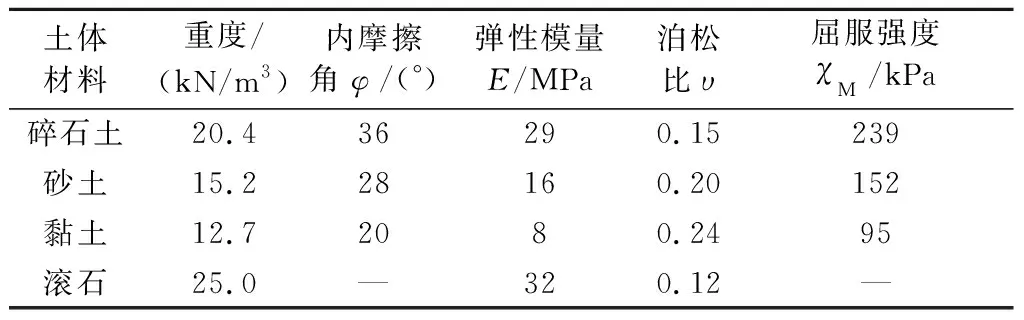
表1 垫层土体材料参数

LS-DYNA的数值计算模型及滚石冲击垫层土体后0.015 s、0.045 s及0.06 s时的Von mises应力云图如图3所示，根据图3中的应力等级色条便可得出土体垫层各部分的应力分布情况，同时也可判别相应的弹塑性区域.

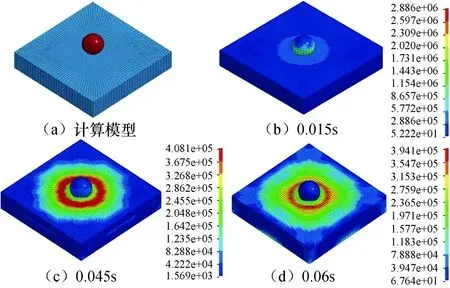
图3 LS-DYNA数值模拟结果Fig.3 LS-DYNA numerical simulation results

滚石的冲击力随时间的变化曲线如图4所示.由图4可见，在滚石冲击0.004 s后，滚石的冲击力即达到峰值，而在此后的0.004～0.048 s期间，滚石的冲击力在逐步的震荡过程中减小至0，滚石冲击过程完成.

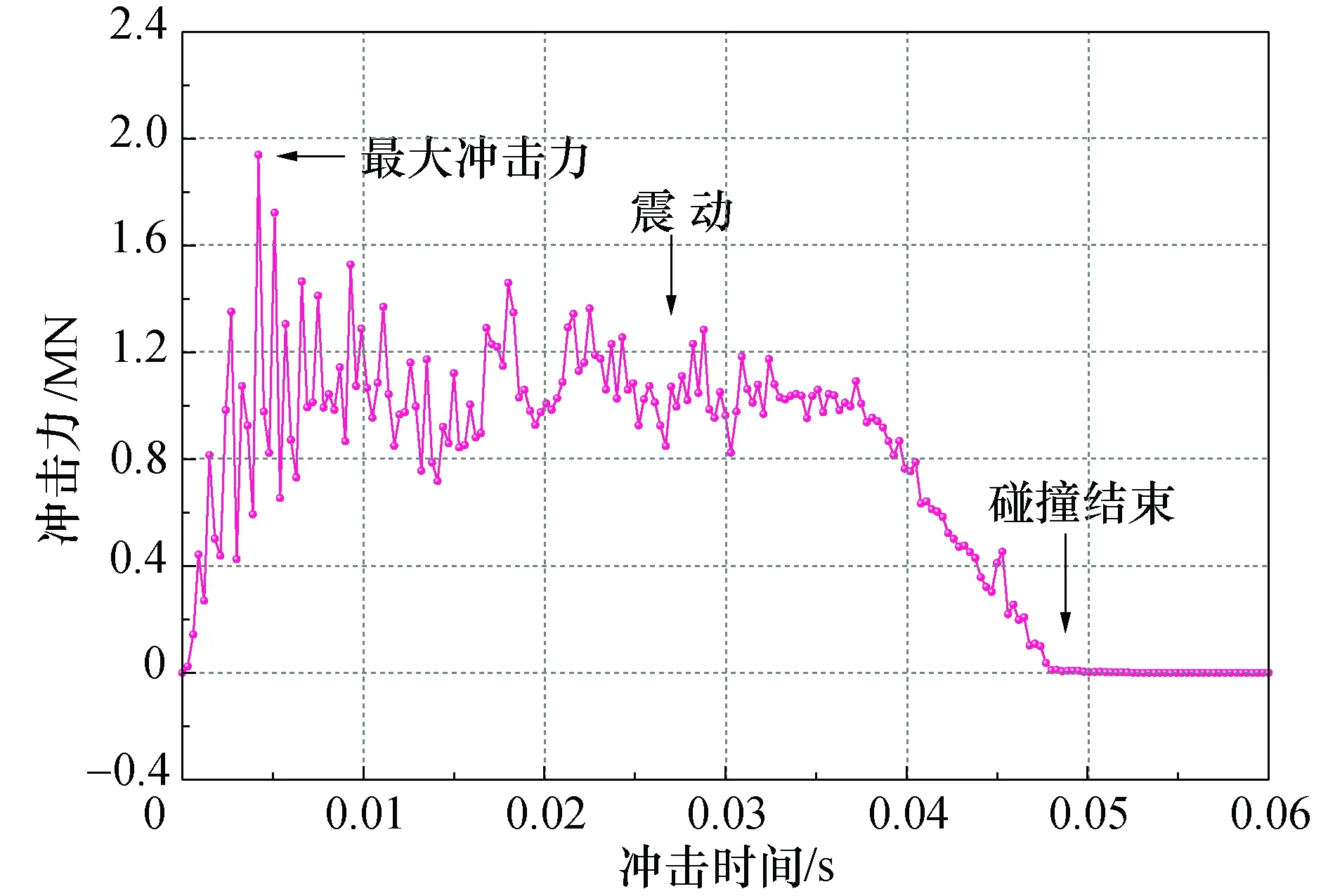
图4 冲击力的变化曲线Fig. 4Variation curve of impact force

滚石冲击过程中侵彻深度随时间的变化曲线如图5所示.可见在0～0.034 s期间，滚石的侵彻深度将会随着冲击时间的增加而呈现出近抛物线的增加趋势，且在0.034 s时形成最大冲击坑深0.301 m，而在0.034～0.048 s期间，产生了约2.6 cm的回弹，并最终形成了0.275 m的冲击坑深.

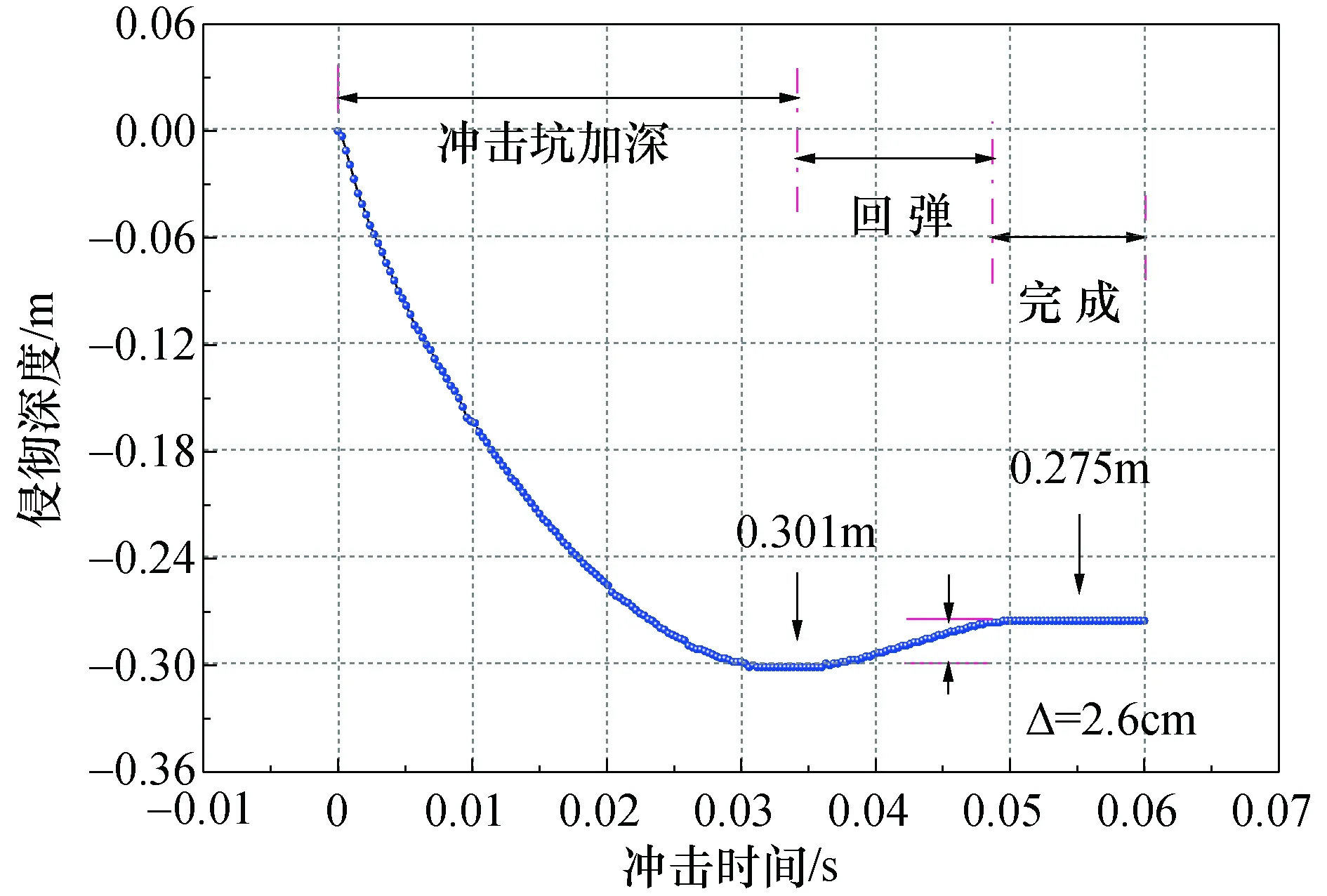
图5 侵彻深度的变化曲线Fig. 5Variation curve of penetration depth

滚石冲击结束后，垫层土体结构中轴线上的各节点的最终位移如图6所示.

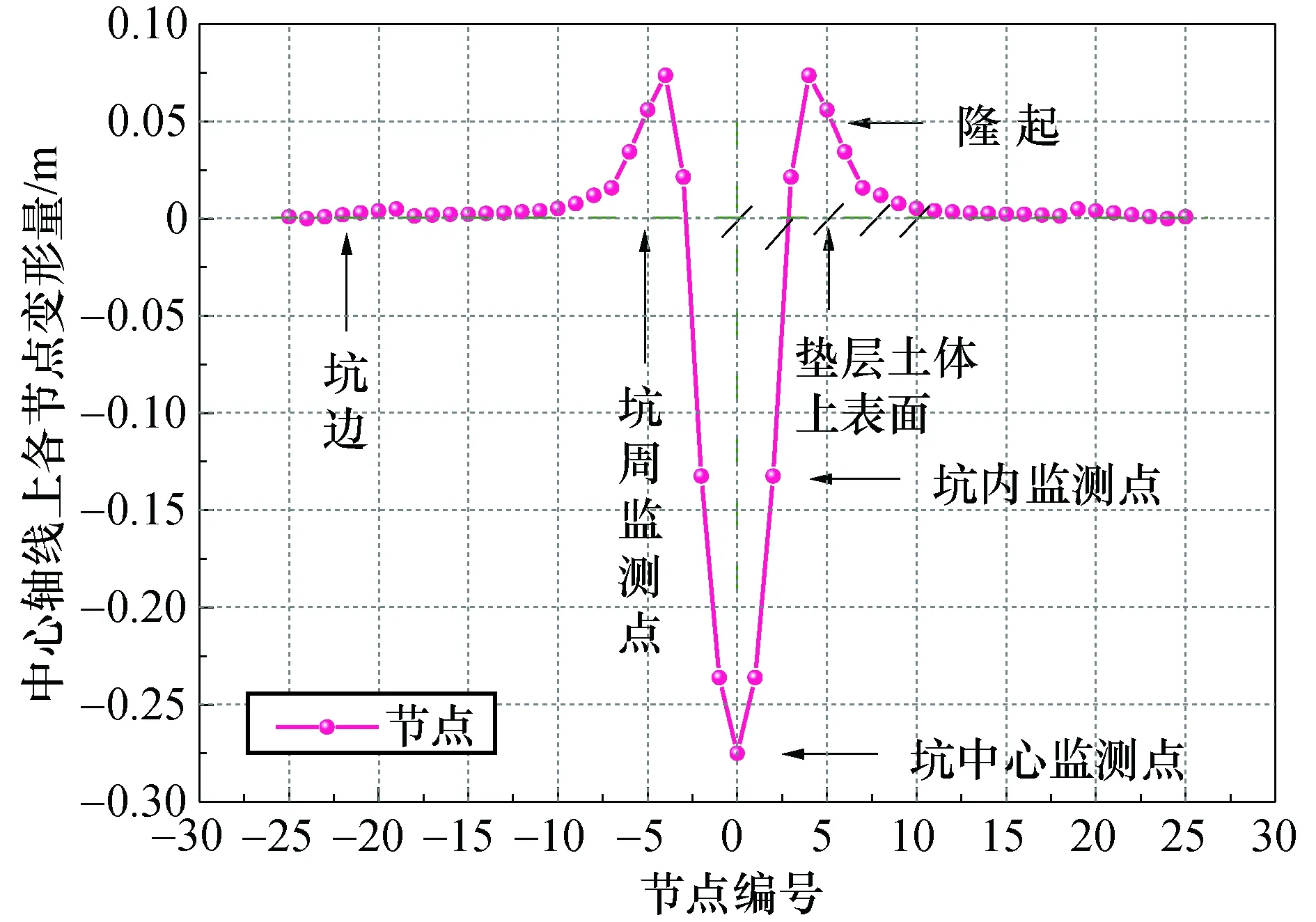
图6 冲击坑的位移曲线Fig.6 Displacement curve of impact crater

可见冲击坑横剖面的左右两侧形状对称，冲击坑中心所形成的最大位移变形为0.275 m，并在坑的周围形成了约8 cm的隆起，垫层土体发生变形的主要区域是坑中心处半径为0.5 m圆的范围.

4 计算结果对比分析

为对各算法下滚石冲击力的计算结果进行对比分析，选取滚石半径为0.5 m，滚石质量为1 308.25 kg，垫层厚度取为1 m，其余的计算参数见表1及表2，计算工况中的各计算参数参考文献[20-21]进行选取，各种算法的计算表达如下[22].

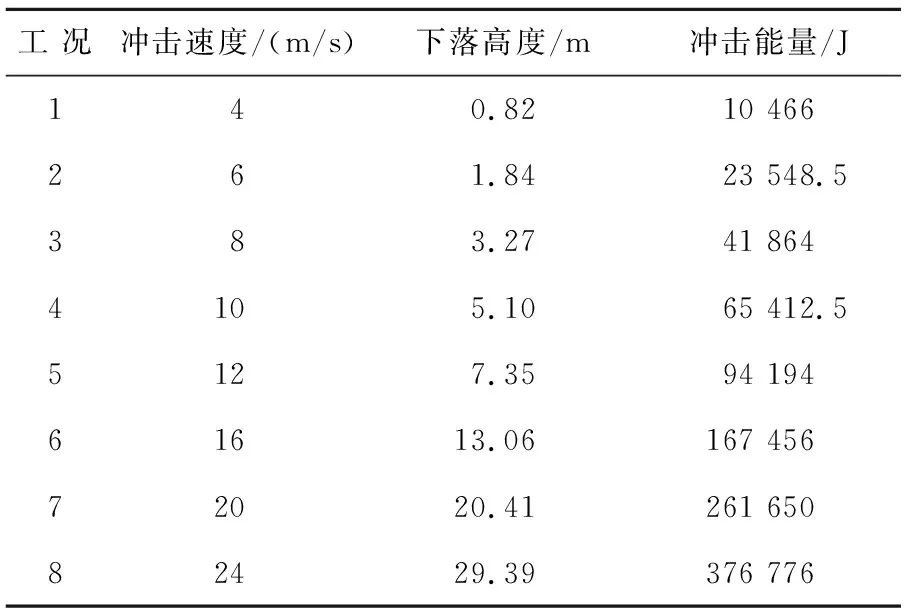
表2 滚石冲击力计算工况表

1)Hertz算法：

(33)

2)瑞士算法：

(34)

3)日本算法：

(35)

4)隧道手册算法：

(36)

(37)

(38)

式中：ME为垫层土体弹性模量；ε为拉梅常数；v0为滚石初始冲击速度；vc为滚石冲击垫层的压缩波速.

碎石土、砂土、黏土垫层情况下垫层各算法所得出的滚石冲击力如图7～图9所示.通过对图7～图9进行分析，可得出如下结论：

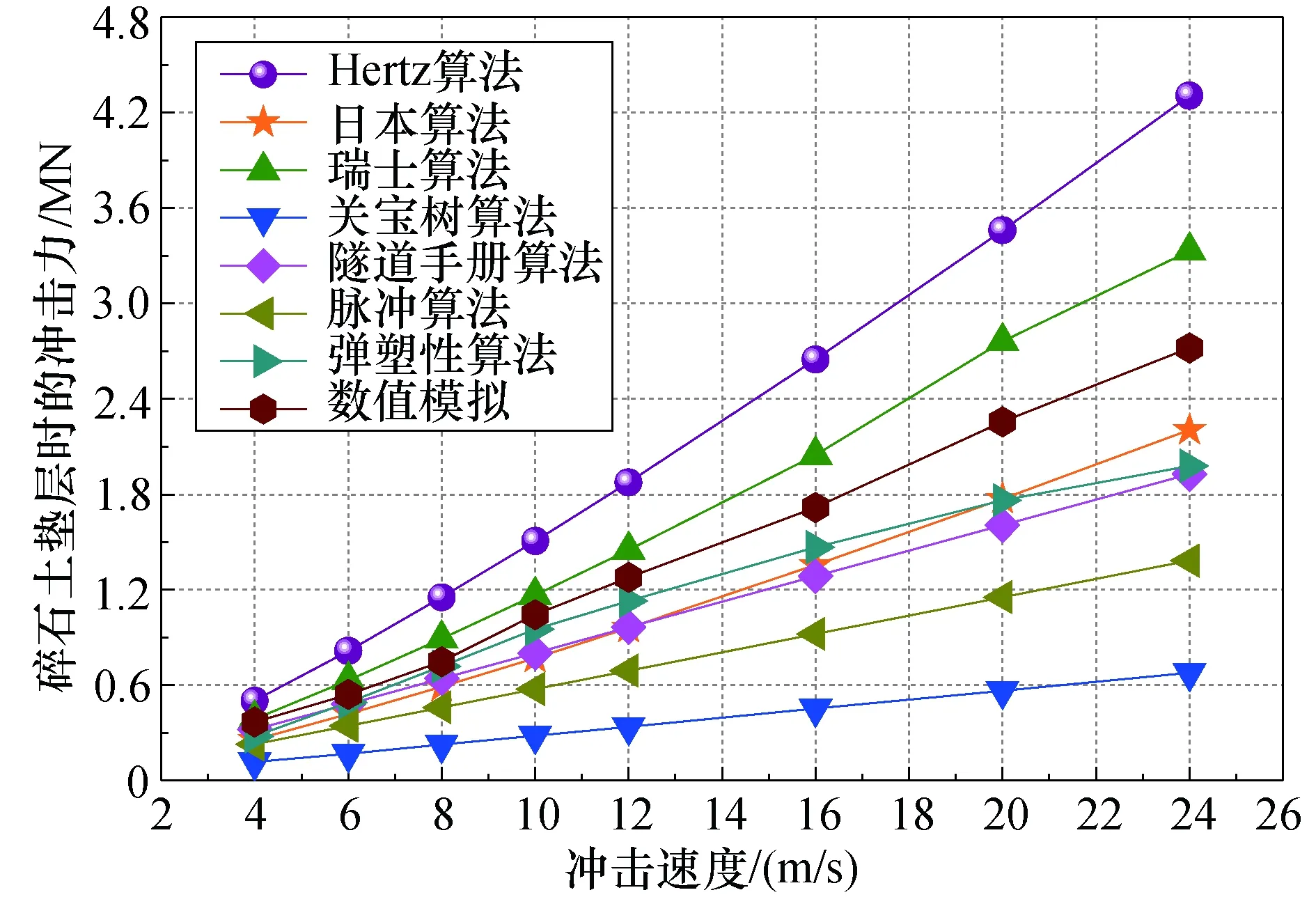
图7 碎石土垫层的“冲击速度-冲击力”曲线Fig.7 “Impact speed - impact force” curves of gravel soil cushion

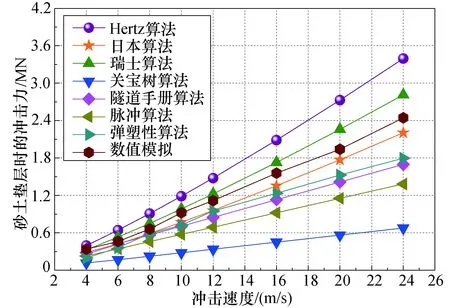
图8 砂土垫层的“冲击速度-冲击力”曲线Fig. 8 “Impact speed - impact force” curves of sandy soil cushion

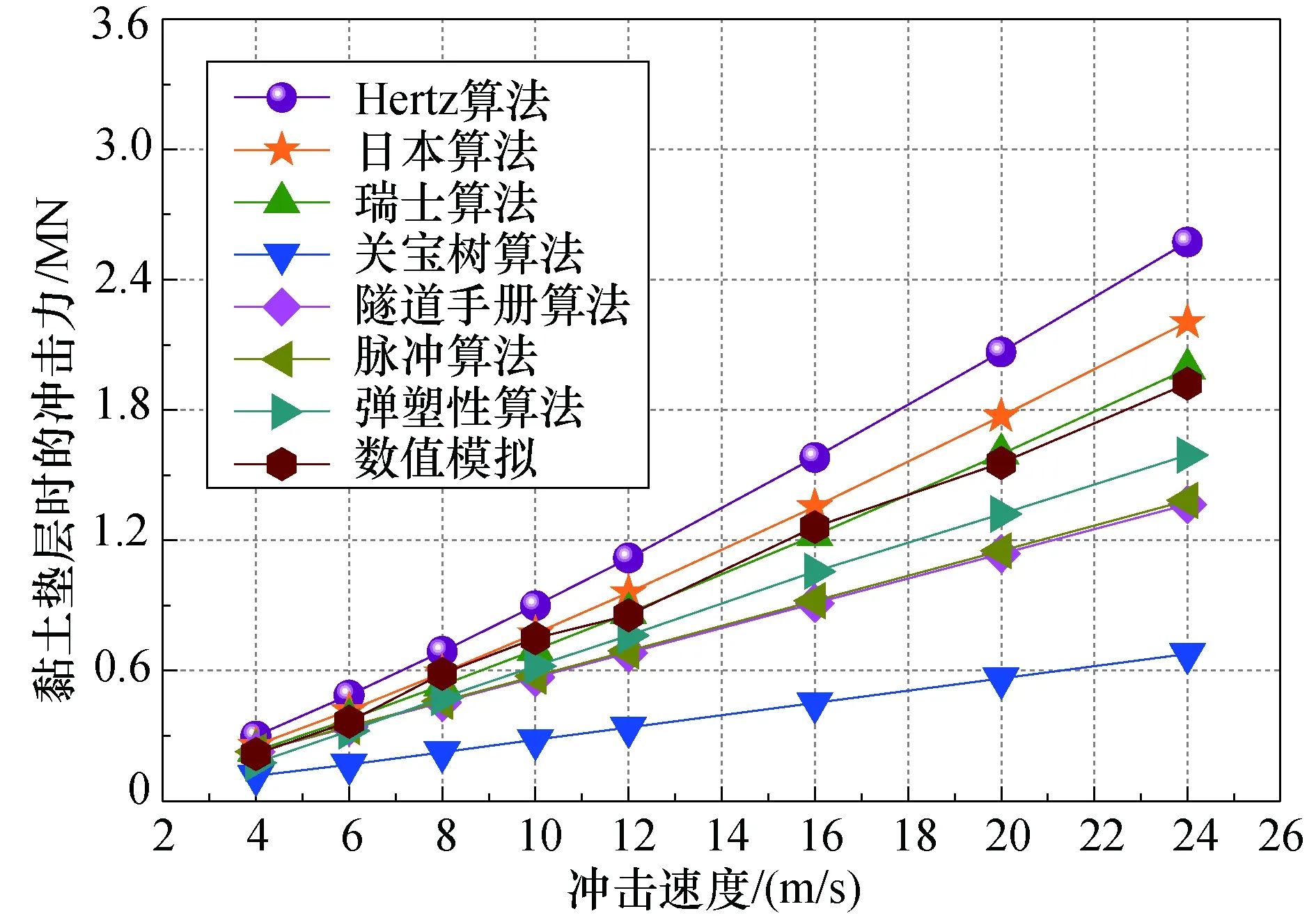
图9 黏土垫层的“冲击速度-冲击力”曲线Fig. 9 “Impact speed - impact force” curves of clay cushion

1)Hertz算法所得出的滚石冲击力值无疑是偏大的，这主要是由于该算法是基于完全弹性理论所得出.瑞士算法结果略微偏大，因为该算法考虑了垫层材料的弹性模量的影响，并取弹性模量值的2/3次方作为因子，同时瑞士算法明显满足P碎石土>P砂土>P黏土，而当垫层土体为黏土材料时，瑞士算法冲击力已小于日本算法，由此可见，瑞士算法结果整体较大，同时垫层土体的弹性模量对瑞士算法结果影响较大.

2)日本算法所得结果整体较为偏大，且冲击力值整体较为稳定，是因该算法考虑将滚石重力值的2/3次方及下落高度的3/5次方作为滚石冲击力的计算因子，而拉梅常数值一般取为106.

3)关宝树算法所得出的计算结果整体偏小，这是由于其算法所得出的冲击力为整个冲击过程中的平均冲击力值，且实验过程中选用的是5 N及8 N的试验锤，或有可能存在一定的局限性，当试验中的滚石质量达到13 082.5 N时，关宝树算法可能会存在一定的偏差，从而导致计算结果偏低.

4)隧道手册算法所计算出的冲击力值普遍偏小，是因为在该算法中滚石冲击力时间的计算是通过2倍的垫层厚度与压缩波速之比所得出的，垫层厚度直接影响到冲击时间，故而冲击时间势必存在一定的偏差，最终致使冲击力与实际存在偏差.

5)LS-DYNA数值模拟结果与日本算法、瑞士算法、弹塑性算法及脉冲算法之间的吻合度较好，实现了各算法之间相互验证.脉冲算法整体与日本算法、瑞士算法及数值模拟算法保持一致，但仍略有偏小.弹塑性算法与日本算法、瑞士算法、数值模拟算法及脉冲算法整体一致性较好，从而证明了该算法的可靠性，这或可能是由于该算法充分考虑了滚石冲击过程中垫层土体的弹塑性变化情况，从而得出了较为准确的计算公式.

5 滚石冲击力的LS-DYNA算法

由于LS-DYNA数值模拟计算结果为滚石的最大冲击力，而隧道手册算法所得出的计算结果为滚石的平均冲击力，且隧道手册算法充分考虑了垫层土体的厚度、弹性模量、密度、泊松比及滚石的重量及下落高度等因素.故而尝试定义将滚石的最大冲击力与平均冲击力之比作为冲击力的放大系数，且给出放大系数的建议值，并通过计算获取碎石土、砂土及黏土垫层的滚石冲击力放大系数ζ与滚石冲击速度v0之间的关系，建立v0-ζ散点图，并进而拟合出相应的滚石冲击力放大系数曲线，具体见图10.

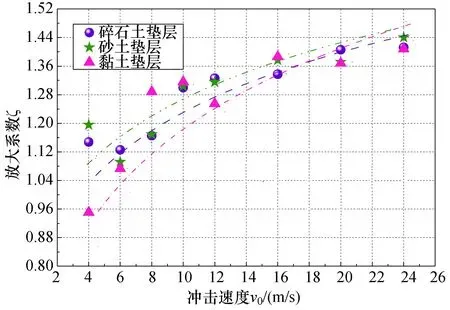
图10v0-ζ曲线Fig.10v0-ζ curves

对于碎石土、砂土及黏土垫层，其滚石冲击力的放大系数曲线表达式为

(39)

式中：ζ碎石、ζ砂土、ζ黏土分别为碎石土垫层、砂土垫层、黏土垫层时的冲击力放大系数.

鉴于式(39)中3条拟合曲线之间存在较小差异，故在综合考虑滚石冲击过程中的多方因素后，得出最终统一的冲击力放大系数ζe的表达式

ζe=0.655+0.241ln(v0+2)

(40)

联立式(36)～(38)、(40)，并考虑滚石恢复系数的影响，从而得出滚石冲击力为

(41)

在考虑滚石冲击角度及滚石自重因素的影响后，得出滚石最大冲击力的LS-DYNA算法的最终表达式，定义为LS-DYNA算法

(42)

式中：θ为滚石冲击速度与垫层土体表面的夹角；β为滚石重力的方向与垫层表面的夹角.

为验证式(42)的准确性，将其计算结果与Hertz算法、日本算法等8种算法的计算结果进行对比，并分别考虑碎石土、砂土及黏土垫层的情况，对比结果如图11～13所示.

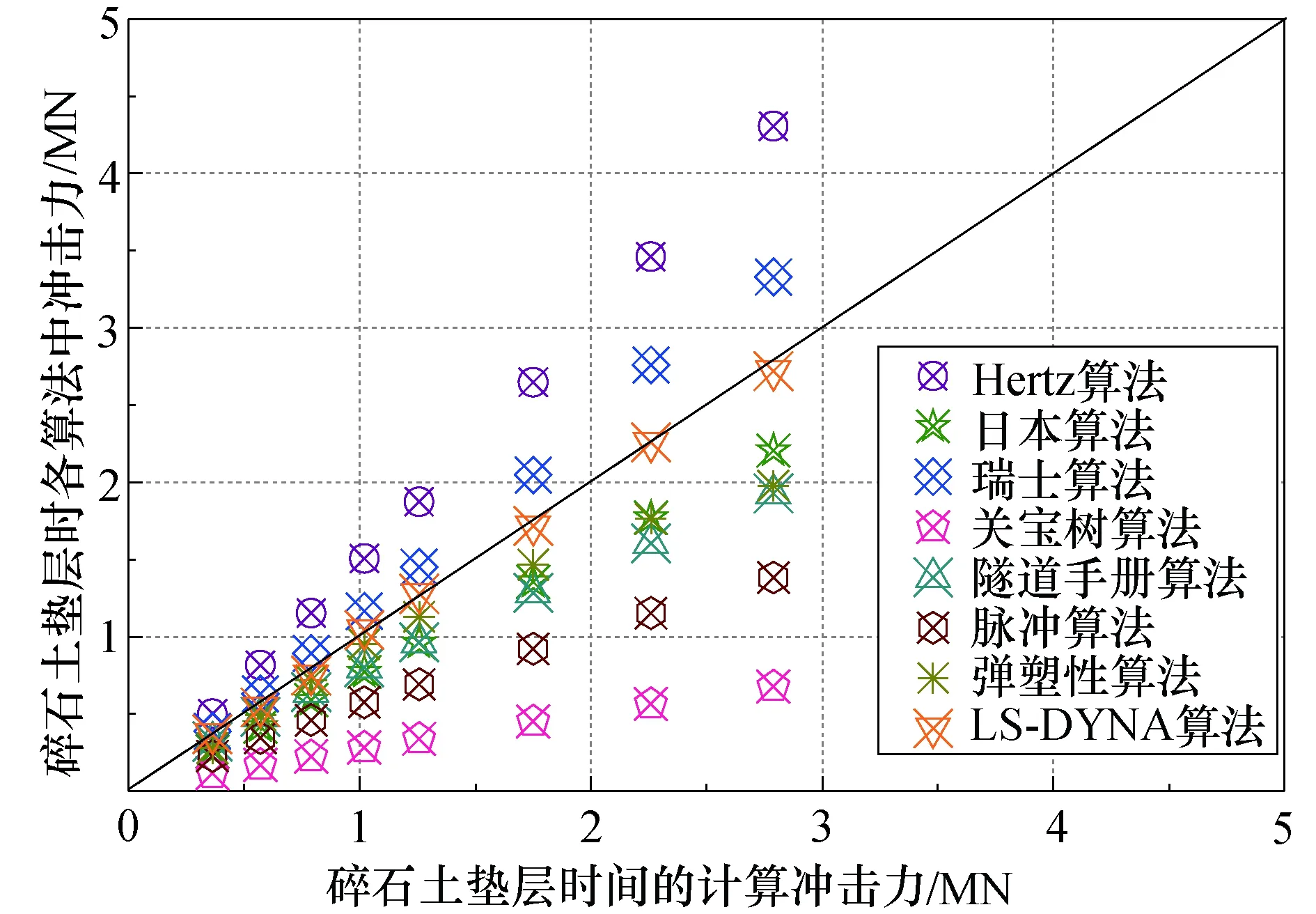
图11 碎石土垫层的验证结果Fig. 11Verification results of gravel soil cushion

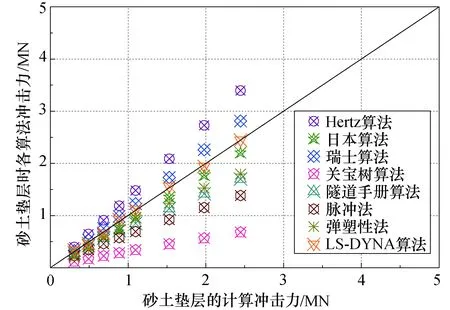
图12 砂土垫层的验证结果Fig.12 Verification results of sandy soil cushion

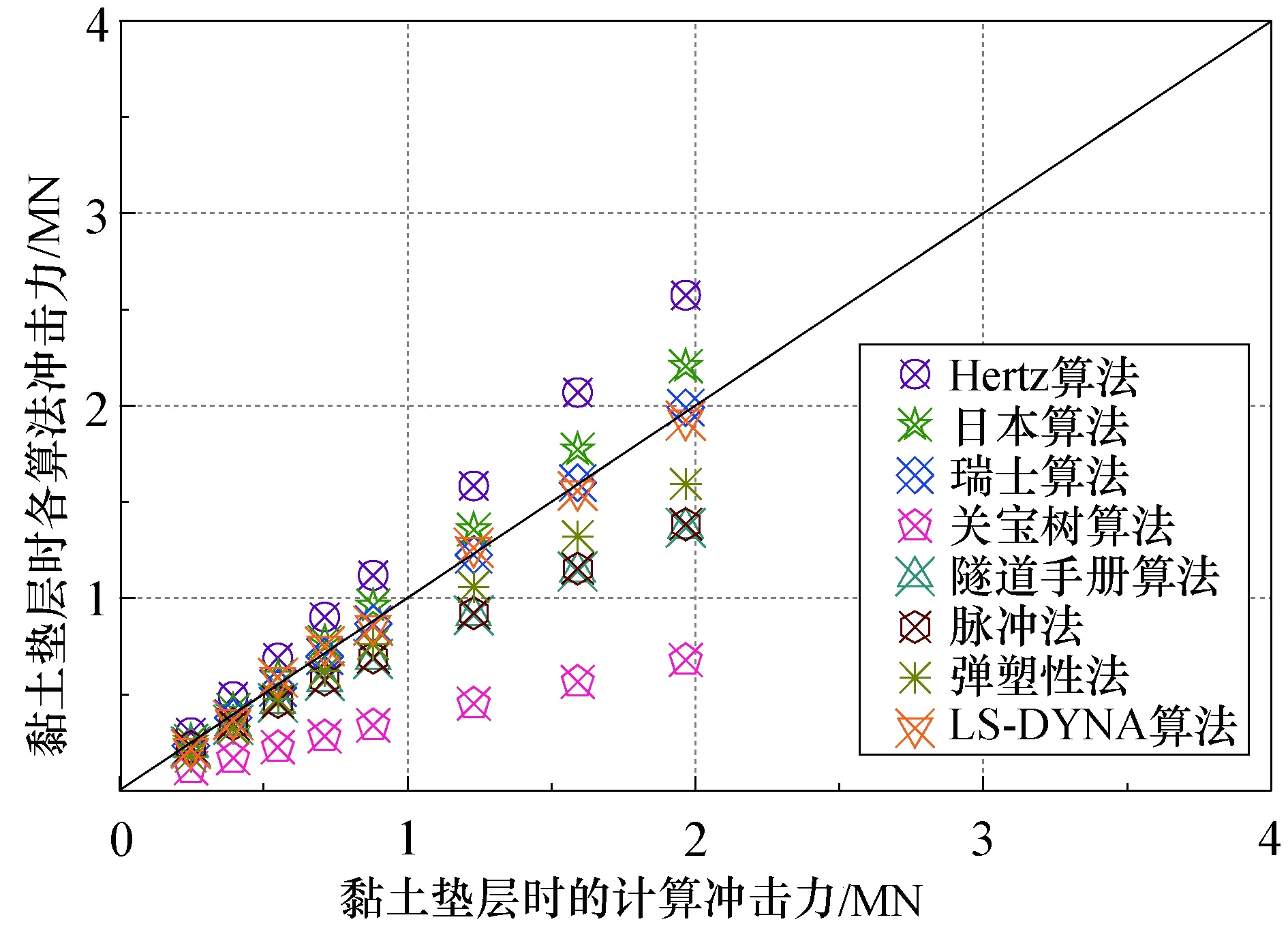
图13 黏土垫层的验证结果Fig. 13Verification results of clay cushion

可见LS-DYNA算法结果与日本算法、瑞士算法、数值模拟结果、弹塑性算法及脉冲算法结果具备较好的一致性，脉冲算法及隧道手册算法结果仍略微偏小，而Hertz算法仍明显偏大，而关宝树算法无疑偏小，与之前的对比验证结果保持一致，其较好地验证了式(42)的准确性.

在得出滚石最大冲击力值后，此时便可结合文献[12]计算出滚石冲击力作用在防护结构顶板上的压力q，见图14.

图14 防护结构顶板上的冲击压力Fig. 14Impact pressure on roof of protective structure

由图14可知q为

(43)

假定滚石冲击力作用于防护结构顶板上部的垫层的面积为滚石球体的等效截面，即落石等效直径为2R1的区域.其中在隧道手册算法中中假定θ为30°，而在路基规范中假定θ为35°，此处由文献[22]可得

θ=45°-φ/2

(44)

式中：φ为垫层土体的内摩擦角.

6 结论

1)基于关宝树算法以及滚石冲击力的脉冲式变化规律，同时考虑了滚石冲击恢复系数的影响，得出了滚石冲击力以及侵彻深度的脉冲算法.结合滚石冲击过程中垫层土体的弹塑性变化过程，建立了滚石冲击力的力学平衡关系式，并基于侵彻深度与接触半径之间的关系，推导出了滚石冲击力的弹塑性算法.

2)通过采用LS-DYNA软件分析研究了滚石冲击垫层土体的微观力学响应机理，得出了滚石冲击力及侵彻深度随冲击时间的变化规律，并给出了最终塑性冲击坑的形状.

3)结合具体的滚石冲击计算工况，对各算法进行了对比分析.研究结果表明：完全弹性的Hertz算法结果明显偏大，日本算法、瑞士算法、数值模拟算法、脉冲算法、弹塑性算法结果吻合性较好，但相互之间存在少量差异，脉冲算法及隧道手册算法略微偏小，关宝树算法则明显偏小.

4)以数值模拟结果及隧道手册算法为基础，建立了v0-ζ之间的拟合曲线，并在考虑κ、θ、滚石自重影响的基础上，得出了滚石最大冲击力的LS-DYNA算法，最终结合8种算法结果对LS-DYNA算法的适用性进行了验证.