基于自由曲面类零件的球头立铣刀切削力建模
蔡永林,鞠 楠
(北京交通大学 机械与电子控制工程学院,北京 100044)
自由曲面类零件主要应用于模具、航空航天、汽车制造等领域,此类零件由于几何结构复杂,主要在多轴数控机床上采用切削加工的方式完成加工.在切削过程中,刀具和工件之间的切削力直接影响切
削热的产生、刀具的磨损及表面质量.因此研究切削力的产生机理,并建立切削力预测模型,进而掌握切削力的变化规律对切削加工中的刀具、夹具选择以及工艺参数优化可以起到一定的指导作用.
为了建立切削力模型,研究参数对切削力的影响规律,国内外学者进行了大量的研究工作.Lee等[1-2]通过一系列正交切削实验测得了切削过程中的剪切屈服应力、前刀面上的平均摩擦力系数以及剪切角等参数,采用经典的斜角切削变换方法得到了球头立铣刀切削刃上切削力的分布情况;姚继铭[3]基于剪切变形理论和摩擦理论,并根据直角切削基本原理以及斜角切削模型,由刀具几何参数、剪切角、摩擦角和切削材料屈服极限推导出了切向、轴向、径向切削力的理论模型;罗智文等[4]针对曲线端铣加工工艺,提出了一种以斜角切削为基础的切削力建模方法,根据最小能量原理,构建了微元刃中力矢量、速度矢量、流屑角、法向摩擦角、法向剪切角及剪应力等切削参数之间的约束;Hendriko等[5]使用解析边界模拟的方式建立了仿真系统,用于计算采用环形刀加工时的切屑几何体以及切削力;Nishida等[6]建立了一种用于球头刀切削力预测的仿真平台,通过体素模型表达刀具切削刃和工件在当前时刻的几何形状,并计算出加工过程中未变形切屑厚度的离散值,进而得到切削力;Irgolic等[7]通过人工神经网络模型对切削深度、进给速度等工艺参数和切削力的关系进行建模;王立涛等[8]通过多因素正交铣削实验,得到了航空铝合金7050-T7451的切削力经验公式模型.
综上,对于切削力建模主要有理论分析法、有限元仿真法、神经网络模型法以及经验公式法.理论分析往往需要对实际问题进行大量简化,因此得到的切削力模型必然存在偏差;采用有限元仿真计算切削力通常需要的计算量大,且当加工对象改变时必须重新进行计算;神经网络模型法和经验公式法本质上都属于一种数据拟合的方式,区别在于二者采用的拟合函数不同,但为了保证模型的可靠性都需要进行大量的切削实验以获取切削力数据.本文作者采用的切削力模型认为切削力和切削载荷存在比例关系,比例系数即为切削力系数,该系数可通过少量实验获得,所得到的切削力模型具有较大的使用价值,可以用于切削工艺参数的优化.
1 刀具几何模型的精确数学描述
切削力在刀具刃线上的分布规律和刀具的几何结构有关,为了建立描述球头刀铣削过程的切削力模型,需要对球头刀的刃线进行数学建模.首先以刀尖点为原点,刀具轴线为Z轴,以经过刀尖点并和刀具刃线相切的直线为X轴,建立刀具局部坐标系,并在该坐标系下采用广义螺旋运动理论描述刀具球刃部分曲线.根据球头刀的几何特征,可以沿轴线将其划分成圆柱体和球头两部分.刀具球头部分刃线的几何抽象如图1所示,对于半径为R的球头刀,将刀具球刃视为点Q绕某个固定回转轴做广义螺旋运动形成的轨迹.
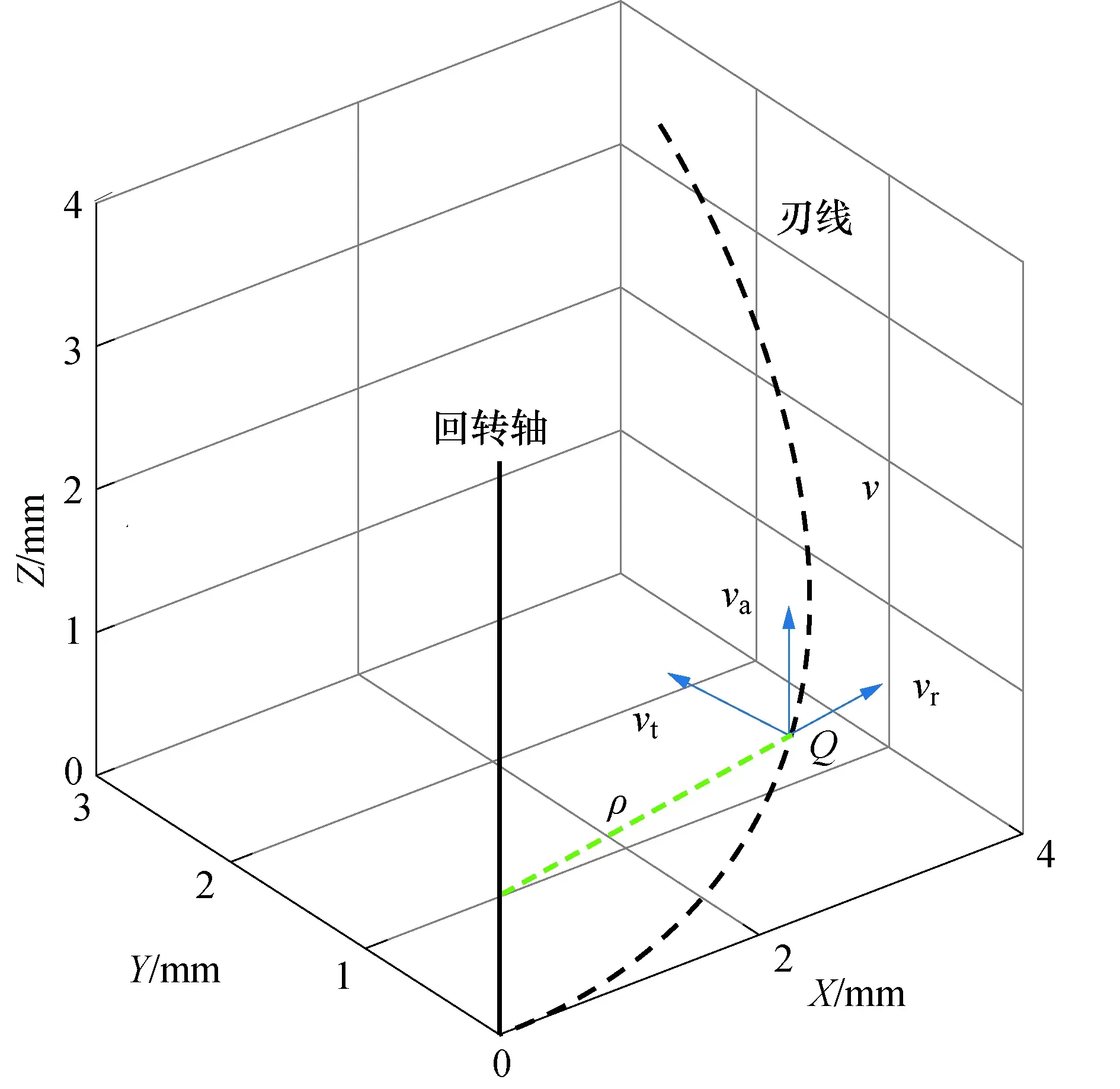
图1 刃线几何结构Fig.1 Cutting edge geometry
点Q处于其轨迹上任意位置时都可以将此时的速度v分解成3个正交分量,即
v=vt+vr+va
(1)
式中:vt、vr和va分别为Q点的周向、径向和轴向速度;ω为Q点的角速度.对于恒定导程球头刀,刃线的导程为定值l,根据运动学关系有
(2)
式中:P为诱导导程,是和刃线导程有关的常数,表示点Q转过单位角度上升的高度.刀具的局部螺旋角β定义为刃线上一点的切线和经过该点的回转面母线的夹角,任意时刻Q点的瞬时转动半径为ρ,且3个速度分量满足
(3)
局部螺旋角β满足
(4)
回转半径ρ和点Q的纵坐标z满足
(5)
将式(5)代入式(4)中可得
tanβ=[R2-(R-z)2]/RP
(6)
对于恒定导程球头刀,刃线上任意一点的局部螺旋角β只与该点的纵坐标z有关,当z=0时,局部螺旋角β=0,当z≥R时,局部螺旋角β达到最大并且保持不变.
2 切削力模型的建立
计算加工过程中的切削力的步骤为:1)将刀具沿刀轴划分成切削微元,对于任意一个纵坐标为z的微元,其厚度为dz;2)根据切削力模型计算参切区域中每个微元的微元切削力矢量;3)计算刃线上参与切削的区域;4) 对微元切削力进行矢量数值积分得到切削力合力,积分限由参切区域确定.
2.1 计算微元切削力
微元切削力如图2所示,对于刀刃线上一点Q,作用在其上的微元切削力可以分解成3个正交分量dFr、dFa和dFt,其中k是点Q对应的轴向位置角.
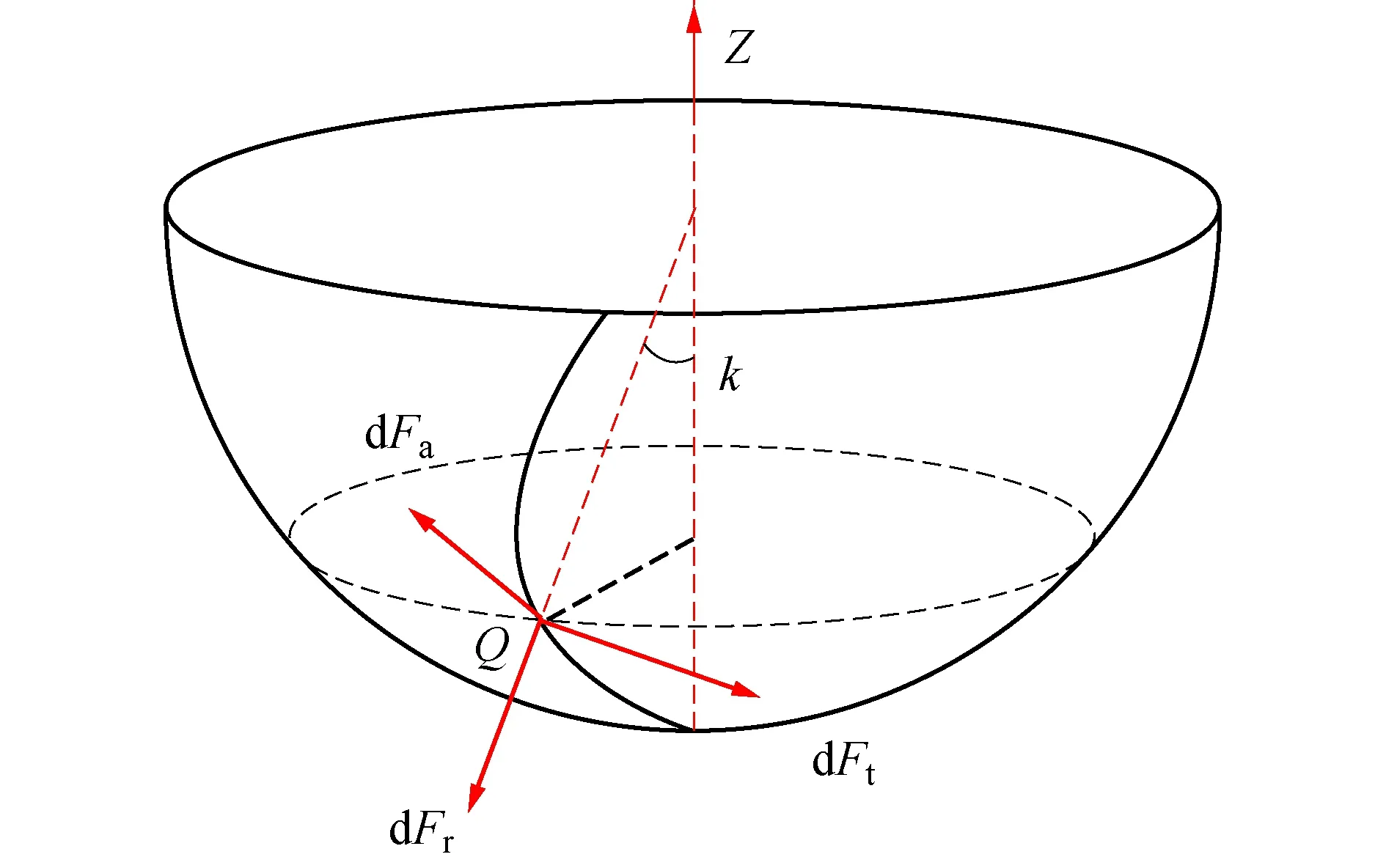
图2 微元切削力Fig.2 Micro-cutting force
根据微元切削力模型各切削力分量满足关系[9]
(7)
式中:dS表示微元切削刃长度;db表示微元切削刃宽度;Kie和Kis分别为两组与刀具几何结构以及材料有关的切削力系数,需通过实验确定,i=r,a,t;tn表示未变形切屑厚度,在数值上等于已加工表面和刀齿下一刀即将加工出的表面的径向距离.
作广义螺旋运动的点Q在t时刻的速度分解图如图3所示,其中vr以及va的合速度为vs,vs和v的夹角即为此时的局部螺旋角β,经过长度为dt的微小时间段之后Q在v和vs方向上的位移分别为dS和db,即
(8)
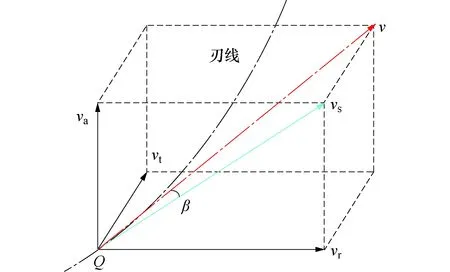
图3 广义螺旋运动速度分解Fig.3 Velocity decomposition of generalized spiral motion
对于平面类零件该参数可通过几何推导得出,加工平面类零件且刀具垂直工件表面的情况下切屑的形成过程见图4.刀具从已加工表面出发,沿进给方向运动到下一个刀位点,刃线的扫略面和工件实体围成的区域构成了即将形成的切屑几何体.
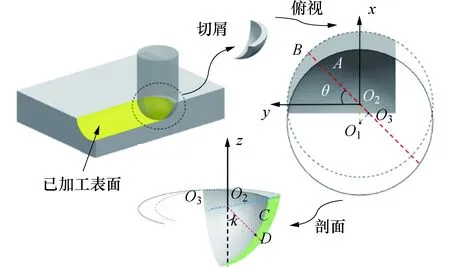
图4 平面类零件切屑形成过程Fig.4 Cutting forming process of plane parts
O1为当前刀具刀心点,O2为刀心点下一位置,两点之间的距离即为每齿进给量fz.刀具半径为R,对于切削刃上一点D,其轴向位置角为k,切入角为θ,过O1做AB的垂线得交点O3.由几何关系可知
(9)
过AB作垂直于平面xO2y的剖面,连接O2D得交点C,CD的长度即为tn.经过几何推导可得
(10)
可知,tn的长度由刃线上点的位置确定.但对于自由曲面类零件,由于刀轴矢量可以处于任意姿态,不能直接得到tn的解析解.故而提出了一种适用于自由曲面类零件的快速计算tn的算法,可以将切削力模型推广到加工任意形状零件的情况.实际加工具有复杂曲面的零件时,刃线上点的运动是刀具自传、平移以及姿态变换的叠加,相邻刀位点之间刃线的扫略面如图5所示,图5中直线为刀具进给方向,螺旋曲线表示刀具刃线,刃线扫掠面几何结构复杂.考虑到刀具的自传速度远大于进给速度,因此可以用球面近似代替图中的扫掠面求解此时的tn,并且将刀具的每次进给等效成加工微小斜面.根据式(10)可知,tn每齿进给量fz以及刃线上点在工件局部坐标系内的位置决定.加工自由曲面类零件时刀具坐标系Ot-XtYtZt和工件局部坐标系Ow-XwYwZw之间的位姿关系如图6所示.Ow-XwYwZw以刀触点为原点,刀触点法矢量为Z轴,进给方向为X轴,通过右手定则确定Y轴.Ot-XtYtZt以刀尖点为原点,刀轴矢量为Z轴,通过刀轴矢量与Ow-XwYwZw中坐标系的矢量叉乘确定其余坐标轴.
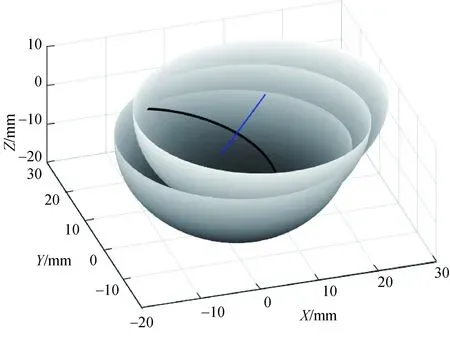
图5 刀具刃线扫略面Fig.5 Sweeping surface of cutting edge
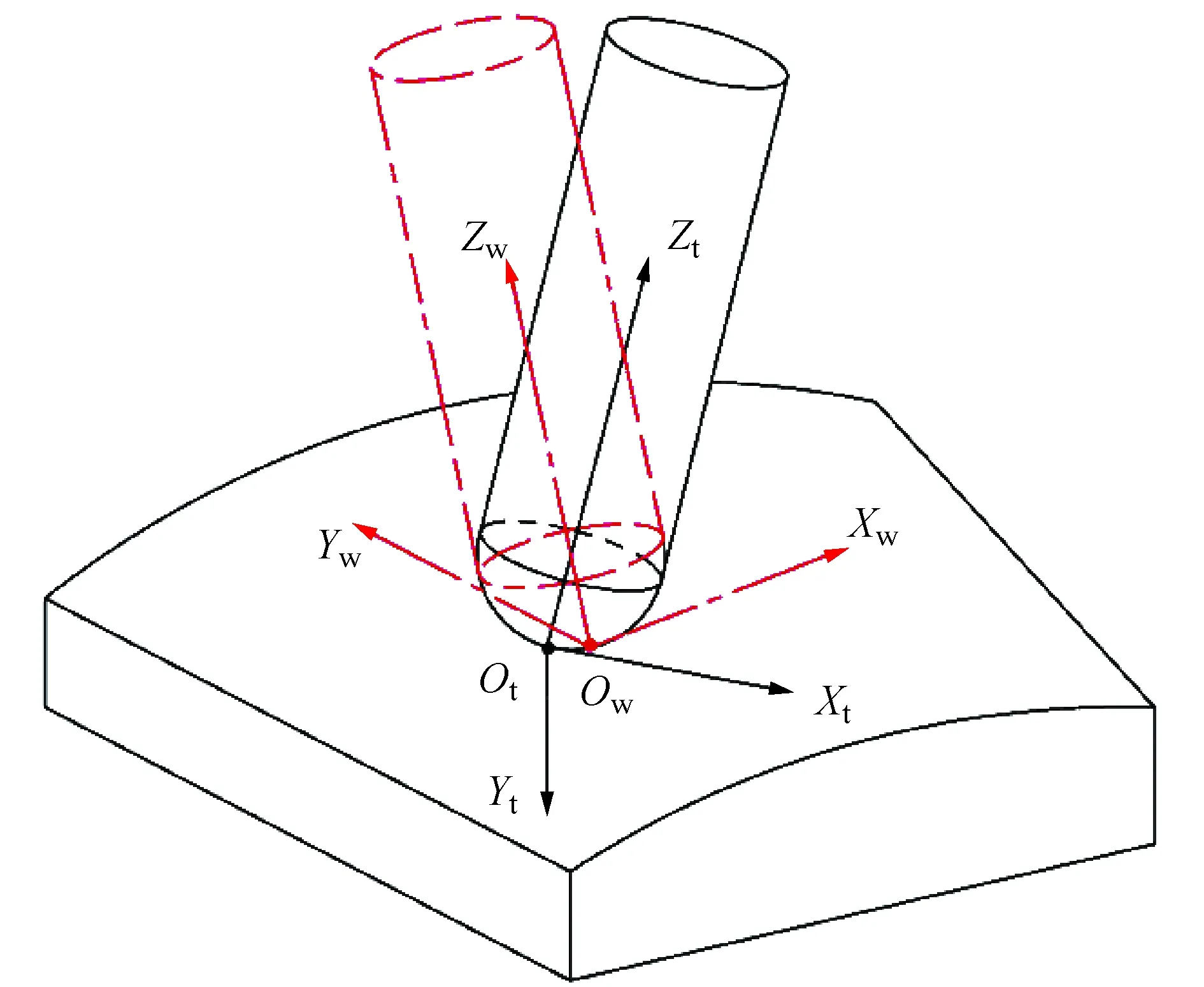
图6 坐标变换Fig.6 Coordinate transformation
定义Ot-XtYtZt和Ow-XwYwZw之间的变换矩阵为Mt,该矩阵由刀轴矢量的姿态确定.刃线上任意一点Q,其在Ot-XtYtZt内的坐标为[x1,y1,z1]T,且有:
(11)
式中:φ0表示z1=0时,刃线的切线与坐标系X轴的夹角;r为中间变量.
根据变换矩阵可知Q点在Ow-XwYwZw内的坐标满足
[x2,y2,z2]T=Mt[x1,y1,z1]T
(12)
则在Ow-XwYwZw中可以计算出对应的切入角θ和轴向位置角k满足
(13)
将式(13)代入式(10)中即可得到适合求解自由曲面类零件加工的未变形切屑厚度tn的算法.
2.2 计算刃线参与切削区域
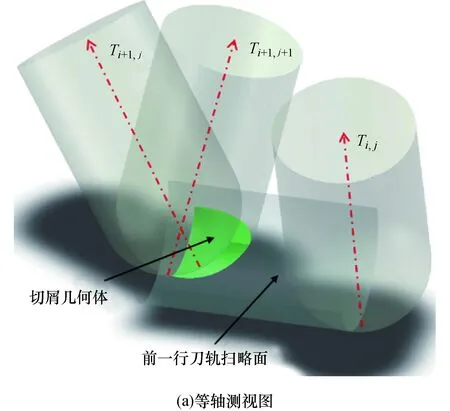
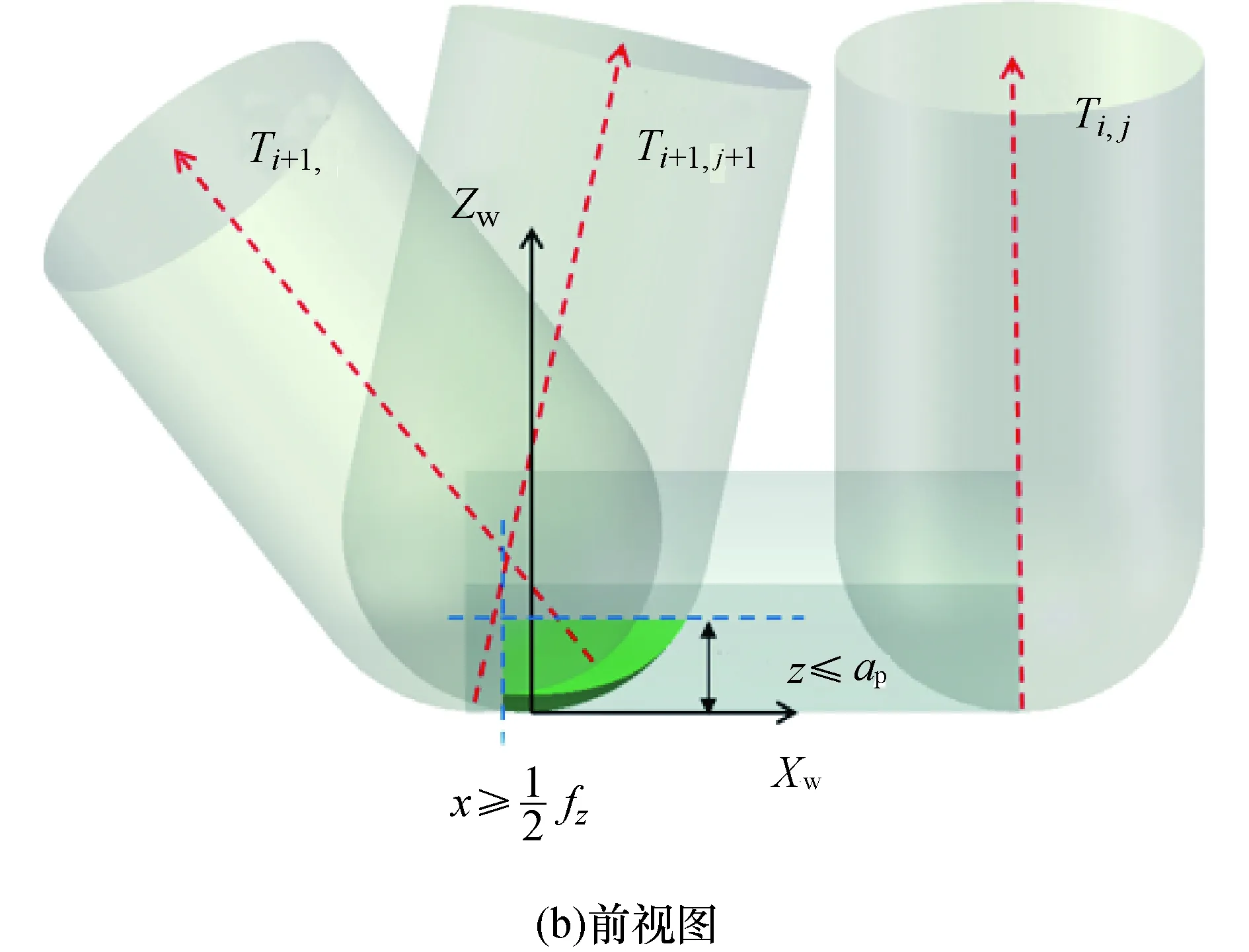
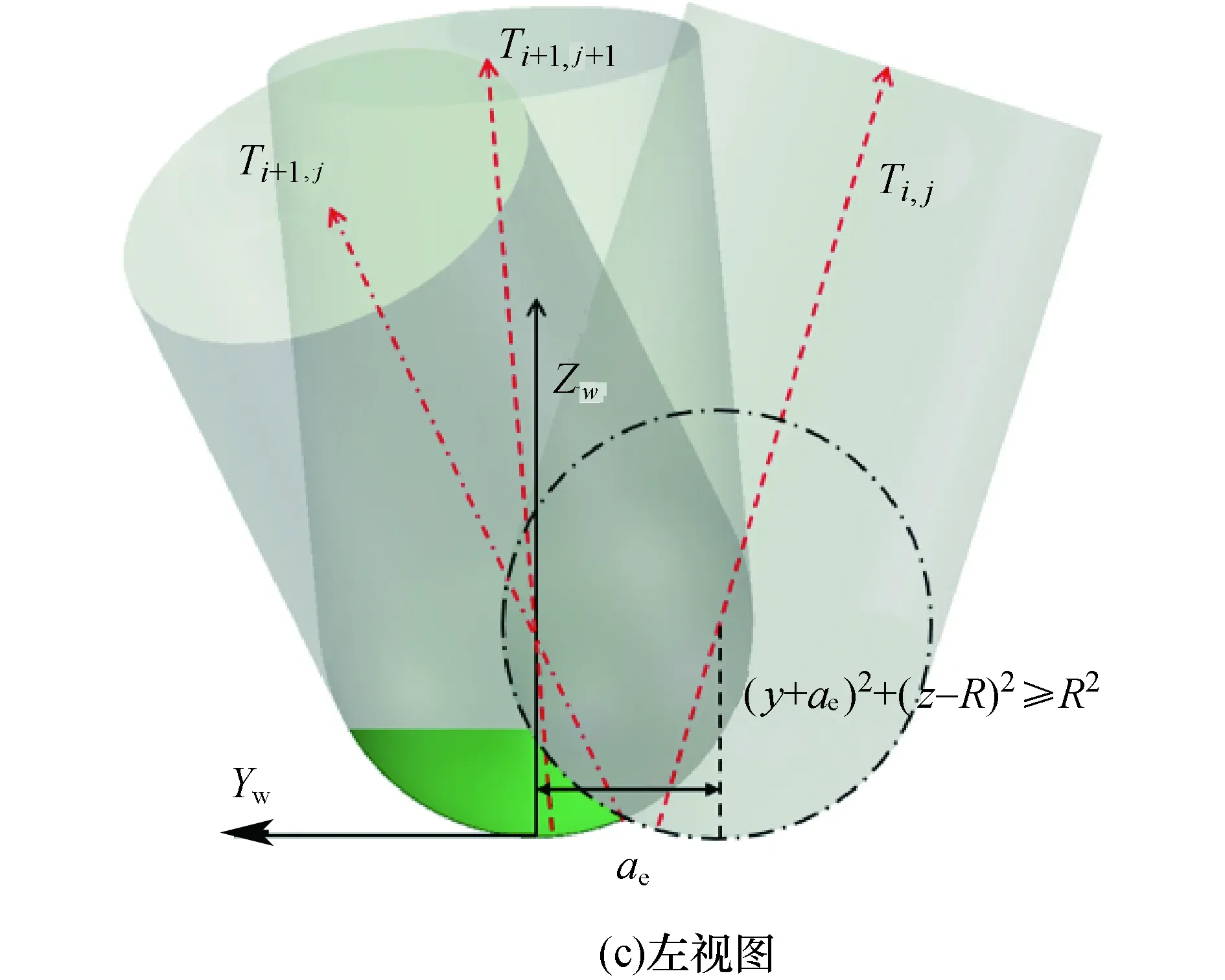
图7 自由曲面类零件切屑形成过程Fig.7 Cutting forming process of free-form surface parts
计算刃线参切区域的目的是确定矢量积分的积分限.刀具对工件进行切削加工过程中,在任意时刻刃线上只有部分微元参与了切削,所有参与切削的微元构成了此时的刃线参切区域,该区域的范围因受到刀轴矢量、切深等因素的影响会发生动态变化.为了确定这一区域,可以采用实体求交或者Z-map[9-10]等方式,但计算效率偏低,在实际应用中受到限制.本文通过分析切屑形成过程,得到了刃线参切区域满足的几何条件,可以快速确定积分限.加工任意形状零件时切屑的形成过程如图7所示.其中Ti,j为刀具位于第i行刀轨的第j个刀位点时的刀轴矢量,相邻两行刀轨之间的距离为ae,切削深度为ap,刀具每齿进给量为fz,切屑几何体是由切深平面、已加工表面和待加工表面所围成的区域.
刀具处于Ti+1,j+1位姿时,刃线上只有一部分微元参与切削,且该部分曲线位于待加工表面上.对于刃线上任意一点Q,其在工件局部坐标系Ow-XwYwZw内的表示为[x2,y2,z2]T,根据切屑几何体的约束条件可知,坐标须满足
(14)
刃线上的参切区域和切屑几何体外表面存在两个交点,可通过二分法确定,两点之间的曲线段构成了参切区域.
3 切削力系数识别实验
3.1 切削力系数识别原理
切削力系数反映了刀具的几何结构以及刀具和工件的材料组合对切削力的影响,与工件的几何特征无关.为建立完整的切削力模型,需要确定模型中的切削力系数Kie和Kis,切削力模型的可靠性在很大程度上取决于切削力系数的准确性,即模型中的切削力系数是否能准确反映实际加工状态.切削力系数识别可归纳为3种方式:
1)平均切削力常系数.
假设切削力系数为常数,但对于球头刀,在刀具球头部分其有效切削半径随切削刃高度而变化,将切削力系数视为常数得到的模型精度较差.
2)正交切削刀斜角切削系数变换.
通过几何变换将正交切削的系数变换到斜角切削,这种转换是在大量简化假设下建立的,并且需要了解刀具详细的几何参数以及材料的物理性能,在实际应用中受到限制.
3)平均切削力变系数.
将Kie视为常数,考虑到刀具切削半径的变化,将Kis视为切削微元轴向位置z的多项式函数.故本文采用该方法进行切削力系数识别.
采用几何参数已知的球头刀对钛合金平板进行槽切加工,根据不同切削参数的组合可采集到对应切削状态下的切削力.为减少实验误差,对于每种切削状态计算其对应的平均切削力,然后通过切削力模型计算相同切削条件下的理论值,二者建立等量关系,即可求得模型中切削力系数.Kis和切削微元高度z的关系可表示为
(15)
实验的目的即确定式中的多项式系数,设多项式系数组成的列向量为g,通过理论计算得到g的系数矩阵为A,实验测得的平均切削力为列向量F,则有
Ag=F
(16)
可求得切削力系数列向量g为
g=(ATA)-1ATF
(17)
理论上高次多项式的拟合能力较强,可以采用任意高次多项式表达切削力系数,但这会造成ATA趋于病态矩阵,使得实验结果过拟合,综合考虑以上因素,本次实验采用二次多项式表达Kis,同时将Kie等效成常数.
3.2 钛合金槽切实验
实验所需硬件条件有:1)五轴数控加工中心;2)Kistler(9129AA)测力仪以及相关采集设备;3)TC4钛合金毛坯;4)直径为8 mm的双齿球头刀,公称螺旋角30°.由于槽切加工时,刀具轴线垂直工件表面,刀具和工件接触区域的几何结构简单,同时可以减少刀具偏心对实验结果的影响,因此设计了9组不同切削参数组合的槽切切削实验,实验中选用的切削参数如表1所示.
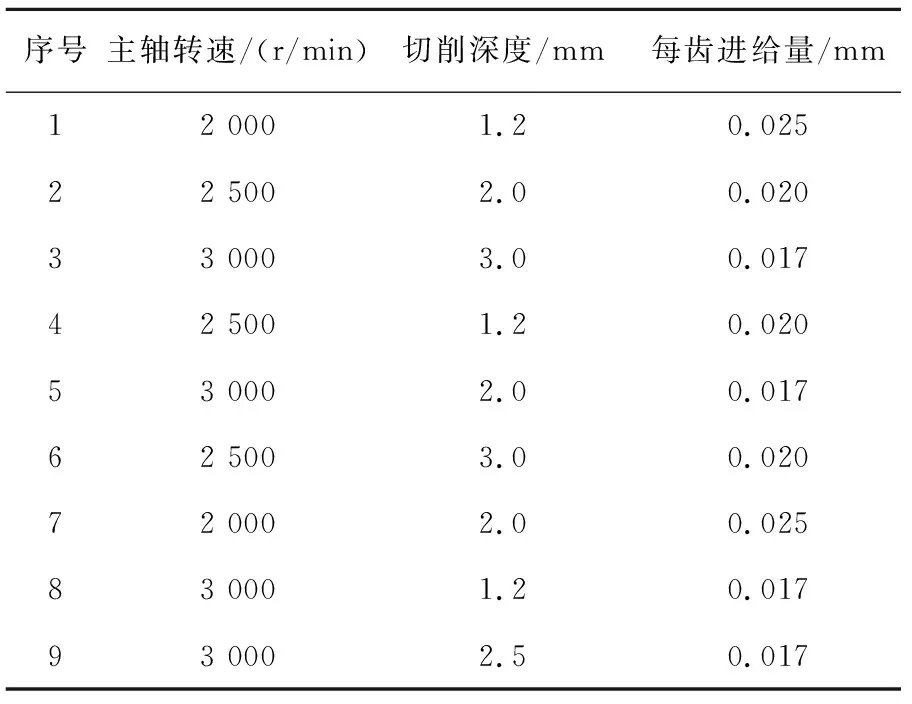
表1 切削参数
切削力系数识别所使用的实验装置如图8所示,毛坯通过紧固螺栓和测力仪连接,刀具按照一定的切深沿直线进给.刀具和毛坯之间的切削力信号通过测力仪的压电传感器被接收设备采集.

图8 实验装置Fig.8 Experimental device
实验得到的不同切削参数下的平均切削力如表2所示.根据1~7组实验平均切削力的实验值可得到切削力系数为
(18)
至此,得到了适合自由曲面类零件加工的完整切削力模型.
表2实验结果
Tab.2 Experimental results N
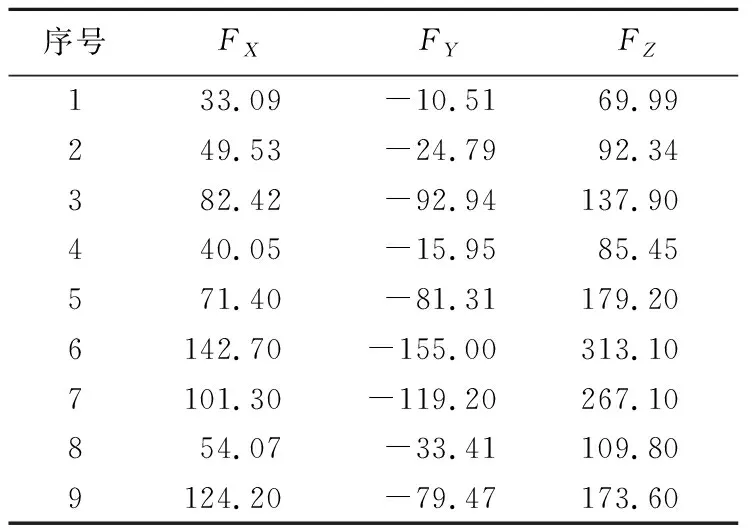
序号FXFYFZ133.09-10.5169.99249.53-24.7992.34382.42-92.94137.90440.05-15.9585.45571.40-81.31179.206142.70-155.00313.107101.30-119.20267.10854.07-33.41109.809124.20-79.47173.60
3.3 切削力模型验证
为了验证得到的切削力模型是否能真实反映实际切削加工中的切削力变化情况.选取第8、9组实验的数据,通过对比切削力的实验值和模型理论值验证模型的准确性.按照切削力模型可计算出刀具处于任意位姿时的切削力合力,但实际加工中由于不能确定在某一时刻刀具转过的角度,因此不能确定模型中的切入角θ,但可计算出刀具处于某个位姿时可能达到的最大切削力,故可通过对比切削力合力的最大值验证模型.以第8组实验的数据为例进行分析实验数据的变化规律.
实验采集到切削力分量FX、FY和FZ随时间的变化以及切削力合力的统计分布如图9所示,由实验结果可知合力呈双峰分布.切削力分量的空间分布如10(a)所示,以模型计算出的当前切削条件下的切削力最大值Fmax为半径,原点为球心作球面得图10(b),该球面是切削力点云数据的一个紧界,计算可知91%的数据位于边界内部,说明切削力系数可靠,切削力模型达到了较好的精度.
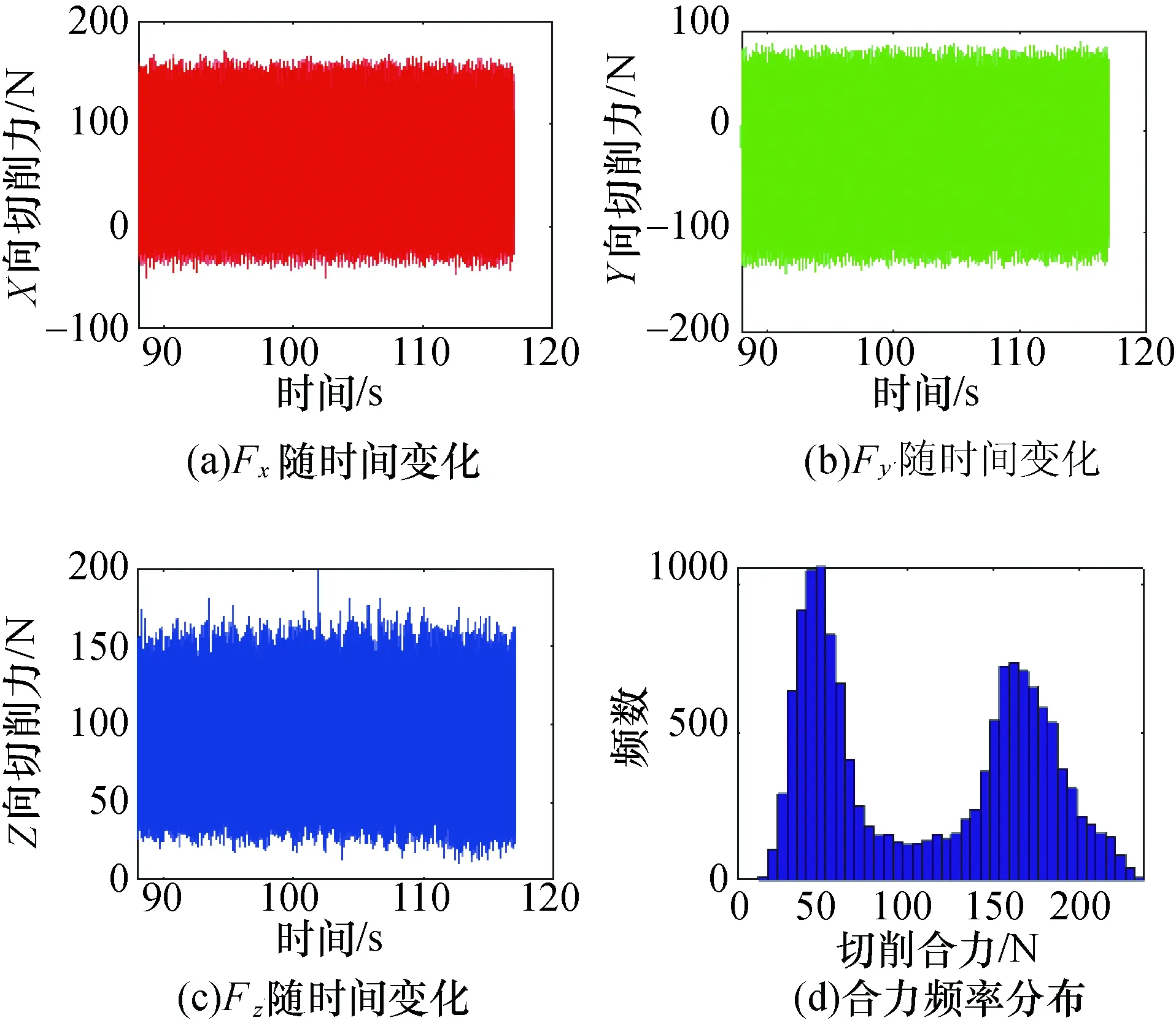
图9 实验结果数据Fig.9 Data of experimental results
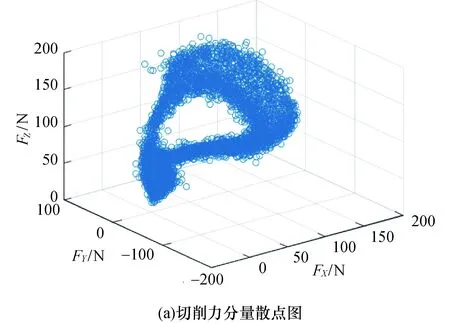
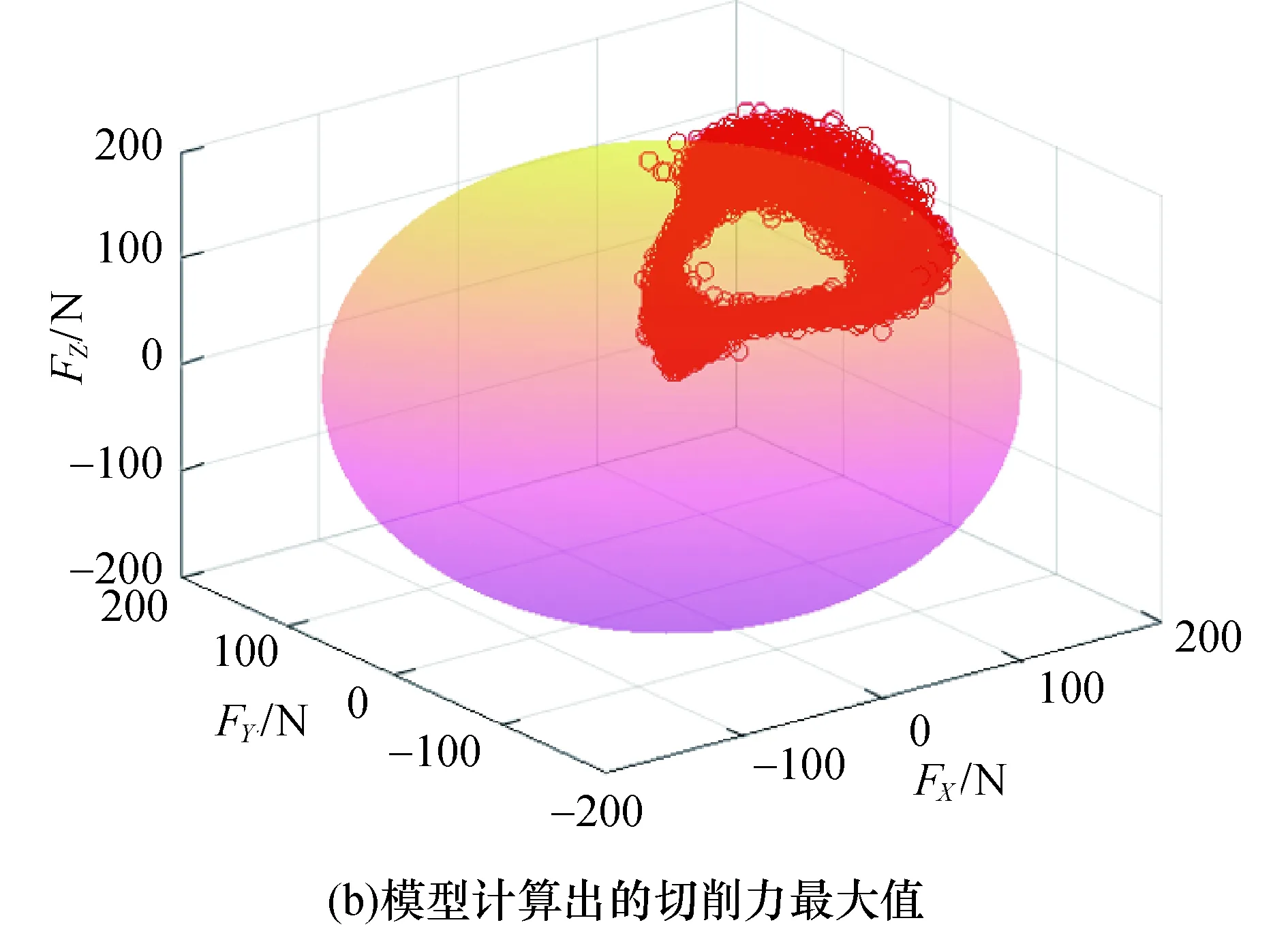
图10 切削力空间分布Fig.10 Spatial distribution of cutting force
4 结论
1)将切削时力计算模型推广到了加工自由曲面类零件的情况,通过钛合金的切削实验得到模型中的切削力系数,计算结果表明模型计算的理论值和实验数据相符.
2)刀轴矢量的变化影响未变形切屑厚度,从而改变切削力的大小和方向.可根据切削力模型在进行刀具轨迹规划时优化每个刀位点的刀轴矢量,以减小切削力和加工变形,提高加工质量.

