微课程教学的设计与实践
汪丽娜 庞晶


[摘 要] 微课程中的“微”既指教学时长短又指教学内容少。一方面,教学时长短便于学生利用碎片化时间学习;另一方面,教学内容少对教师做教学设计提出了更高的要求。文章以概率论与数理统计中最重要的一类定理——中心极限定理为例,阐述微课程教学设计的特点及其应用实践。贴近生活的案例设计使教学更生动;形象化教学使抽象的定理更具象化地呈现。微课程教学实践体现了三个特点:合理的教学结构设置、有针对性地突出重点、加强教学系统性的考量。
[关键词] 微课程;案例设计;数值模拟;中心极限定理
[中图分类号] G642 [文献标志码] A [文章编号] 1008-2549(2019) 09-0110-03
微课程是微型学习的一种具体形式,主要以短时视频为载体记录微型化的教学内容,是对传统教学模式的革新[1]。为贯彻落实《教育部关于全面提高高等教育质量的若干意见》精神,推动信息技术与大学数学课程教学深度融合,促进教师更新教学理念、革新教学方法、创新教学设计、提升教学能力,由教育部高等学校大学数学课程教学指导委员会和全国高等学校教学研究中心共同主办了“全国高校数学微课程教学设计竞赛”,促进了数学类课程教育教学改革的发展、积累了教学成果。
微课程具有短小精悍可重现的教学优势。与传统教学50分钟一节课的安排方式相比,微课程的教学时间较短,更利于集中注意力学习,符合认知规律。其次,微课程是对某个具体的知识点展开教学,与传统教学相比,其主题更加突出、针对性较强。此外,微课程视频易于保存传播,具有更高的教学可重现性,可以供多位教师多次再利用,也可以供学生预习复习使用。本文以概率论与数理统计中最重要的一类定理——中心极限定理为例,阐述微课程教学设计及其实践。文章第一部分介绍中心极限定理的教学特征;第二部分给出中心极限定理的微课程教学设计;第三部分阐述微课程实践的特点。
一 中心极限定理的教学特征
在概率论当中,将“相互独立的随机变量和的极限分布为正态分布”这样的定理统称为中心极限定理。它是概率论当中最重要的一类定理,具有广泛的实际应用背景。例如,应用中心极限定理规划雨量站网设计[2],使得降水监测更科学、经济;应用中心极限定理计算股价期权价格[3];中心极限定理在保险精算[4]等行业中的应用。
多数本科非数学专业概率论与数理统计教材中,中心极限定理包括:列维——林德伯格定理和棣莫弗——拉普拉斯定理。2019年考研数学大纲中对中心极限定理的考试要求是:了解列维——林德伯格定理和棣莫弗——拉普拉斯定理(数学一);了解列维——林德伯格定理、棣莫弗——拉普拉斯定理,并会用相关定理近似计算有关随机事件的概率(数学三)。
中心极限定理的教学安排在随机变量、分布函数、数字特征等先修内容之后,抽样、估计、检验等统计学教学内容之前。从这个意义上讲,中心极限定理可以看作是概率、数理统计两部分的衔接,有着承上启下的作用。一方面,中心极限定理可以刻画正态分布的形成机制,解释正态分布的普遍性;另一方面,中心极限定理是大样本统计推断的理论基石,是学习后续知识的基础。从教学地位、教学目标、教学内容三个方面,中心极限定理都占有重要的位置。与之形成鲜明的对比,在课程考核时,中心极限定理被忽略了。近10年的硕士研究生入学考试中,没有涉及到中心极限定理的考题。
虽然中心极限定理应用广泛、地位重要,但是考试“指挥棒”没有指到这个知识点,造成很多学生学习中心极限定理不够积极,部分教师对中心极限定理的教学不够重视。现有中心极限定理教学中存在一些问题:教学内容缺乏巧妙的设计;教学手段比较简单,形象化演示不足;教学中的应用场景做得不够好,缺乏案例设计。
二 微课程教学设计
中心极限定理从理论上说明了“许多类型”的随机变量, 它们的极限分布服从正态分布, 这既肯定了正态分布在概率论中的重要地位, 也为计算概率提供了强有力的手段。考虑到授课对象是理工科非数学专业本科生,他们的主要专业需求和未来职业需求是应用概率统计的思想和方法。因此,教学设计中, 重点强调中心极限定理的研究对象和应用中心极限定理解决实际问题。选取案例时,选择学生易于产生共鸣的题材;证明定理时,注重形象化的展示;应用定理时,清晰明了地强调如何使用。
列维——林德伯格定理微课程的教学设计以如何设置住宅小区的停车位数量开篇,引出中心极限定理的研究对象:独立随机变量的和。使用数值模拟方式,形象化地展示案例,启发学生提出猜想,引出列维——林德伯格定理。省略定理的证明,采用数值模拟的方法形象化地验证定理内容。最后,使用列维——林德伯格定理计算开篇提出的案例:小区停车位数量问题。
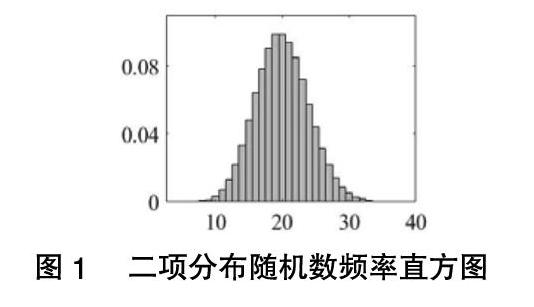
随着私家车保有量的增加,住宅小区停车问题越来越严重。根据小区的地理位置、预期房价、未来业主情况等信息,获知某住宅小区一千户居民的户拥有汽车数量的分布情況,问如何设置该小区的停车位数量,使得每辆车具有一个车位的概率不小于0.97。以此案例开篇,引导学生:已知户拥有汽车量的分布,如果能够得到一千户居民拥有汽车量的分布情况,问题可解。由此引出中心极限定理的研究对象:随机变量和的分布。此外,采用数值模拟的方法将一千户居民拥有汽车数量的分布情况呈现,引导学生大胆猜想:和随机变量服从什么分布。
棣莫弗——拉普拉斯定理微课程的教学设计以二项分布在医学、保险精算、质量检测等方面的广泛应用开篇,提出问题:在分析计算实际问题时,不可避免地涉及二项概率的计算,n较大时直接用公式计算比较烦琐,有更方便的计算方法吗?开门见山地引出棣莫弗——拉普拉斯定理:n充分大时,二项随机变量渐近服从正态分布。从数学证明、数值模拟两个方面验证定理内容。然后,利用定理解决开篇提出的实际问题:保险盈利的概率。

