一类具有时滞和收获的比率依赖捕食模型的分析

武波， 贾建文

山西师范大学数学与计算机科学学院， 山西 临汾 041000

在生物数学的研究中，捕食模型是重要的课题之一. 捕食模型的研究起源于Lotka和Volterra的伟大工作[1]. 后来，许多学者在此基础上选择各种功能性反应函数来更好的研究其动力学性质. 功能性反应函数主要有食饵依赖和捕食者依赖两种类型，例如Holling类[2，3]、比率依赖、Beddington-DeAngelis等.在这些功能性反应函数中，Arditi和Ginzburg[4]指出比率依赖功能性反应函数是较为合理的选择.经典的比率依赖捕食模型可见文献[5，6].

另外，考虑到人类活动的影响，我们在捕食模型中考虑收获项很有必要，早期研究结果表明收获对种群动力学有较大影响.因此，具有收获项的捕食模型被广泛研究[7～9].除此之外，在捕食食饵种群后捕食者的再生过程不是瞬时的，存在时间滞后. 基于上述因素的考虑，我们建立如下具有时滞和收获的比率依赖捕食模型：

(1)

这里x(t),y(t)分别表示在时刻t食饵和捕食者的种群密度. 参数r,K分别表示食饵的内禀增长率及环境容纳量，d是捕食者的死亡率，n,c1,c2分别是半饱和常数，捕食率，转化率.而q1,q2,E1,E2代表收获食饵和捕食者的收获能力系数和努力量. 所有参数都是正常数.

(2)

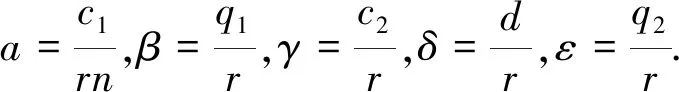
x(θ)=φ(θ)≥0y(θ)=φ(θ)≥0φ(0)>0φ(0)>0θ∈[-τ,0)

(3)

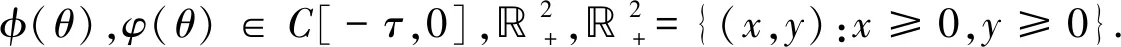
1 解的正性和有界性

定理1 具有初始条件(3)的系统(2)的所有解永远是正的并且最终有界.

证明 系统(2)正性的证明是简单的，因而被省略.下面证明解的有界性.

定义函数W(t)=γx(t)+αy(t+τ),则：对于每一个μ>0，我们有

W′(t)+μW(t)=γx(t)(1-x(t))-γβE1x(t)-αδy(t+τ)-αεE2y(t+τ)+μγx(t)+μαy(t+τ)

≤γx(t)+γ(μ-βE1)x(t)+α(μ-δ-εE2)y(t+τ)n

≤γ+γ(μ-βE1)x(t)+α(μ-δ-εE2)y(t+τ)

令μ=min{βE1,δ+εE2}，则W′(t)+μW≤γ.于是我们有

2 平衡点的存在性和稳定性

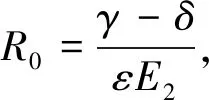
(i)如果βE1<1，则系统(2)总存在轴平衡点S1(x1，0)这里x1=1-βE1.

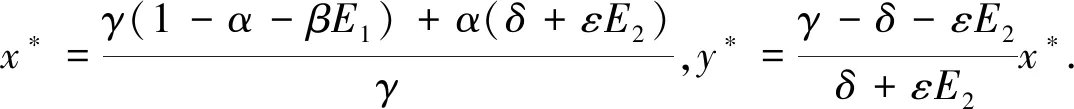
定理2 如果R0>1，则对于任意的τ≥0，轴平衡点S1不稳定；当R0<1时S1局部渐近稳定.

证明 系统(2)在S1点处的特征方程是：(λ-βE1+1)(λ+δ+εE2-γe-λτ)=0.显然其一个特征值λ1=βE1-1<0，其他特征值是方程λ+δ+εE2-γe-λτ=0的根.

令f(λ)=λ+δ+εE2-γe-λτ.

(1)如果R0>1，对于任意的τ≥0，那么我们有

所以f(λ)=0至少有一个正根，从而S1不稳定.

(2)如果R0<1且τ=0，则另一个特征值λ2=γ-δ-εE2<0，故S1局部渐近稳定.

(3)如果R0<1且τ>0，令g(λ)=λ+δ+εE2,h(λ)=γe-λτ.则根据函数g(λ)和h(λ)的图象，可知方程g(λ)-h(λ)=0有唯一的一个负根.所以S1局部渐近稳定.

定理3 如果τ=0且下面的条件成立

(i)α>1,δ+εE2-γ(α+βE1-1)>0. (ii)γ2(α+βE1-1)-α(δ+εE2)2<0.

则系统(2)的正平衡点S*局部渐近稳定.

证明 系统(2)在S*点处的特征方程是:λ2+(a1+a3)λ+a2+a4=0.这里

利用Routh-Hurwitz判据可知，特征方程的两个特征值都具有负实部，即S*局部渐近稳定.

3 Hopf分支的存在性

当τ>0时，系统(2)在S*点处的特征方程是：λ2+n1λ+n2+(n3λ+n4)e-λτ=0.其中

设λ=iω(ω>0)是特征方程的根，则有

由此可得

从而有

(4)

令v=ω2，则方程变为

(5)

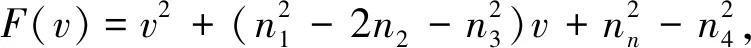
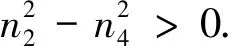
于是得到相应时滞τj的临界值

这里j=0,1,2....假设λ(τ)=ψ(τ)+iω(τ)是S*点处的特征方程的根，它满足ψ(τ0)=0和ω(τ0)=ω0，τ在τ0附近.则我们有下面的横截条件：

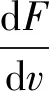
证明 在S*点处的特征方程两边求λ关于τ的导数得到

把λ=iω0代入上面的等式中，便有

通过上面的分析，应用Hopf分支定理，我们有下面的定理：

定理4 假设系统满足下面的条件

(iv)α>1,δ+εE2-γ(α+βE1-1)>0

(v)γ2(α+βE1-1)-α(δ+εE2)2<0

那么系统(2)的内部平衡点S*当τ<τ0时局部渐近稳定， 当τ>τ0时不稳定.也就是说，系统(2)在点S*处当τ=τ0时产生一个Hopf分支.

4 最佳收获分析

在本节中，我们为寻求最佳收获方式，选择目标函数为

(6)

这里c1和c2分别是对食饵和捕食者单位捕获努力量的成本，p1和p2分别是食饵和捕食者单位生物量的价格，ξ代表了瞬时的年折扣率，v1,v2是经济常数.

我们的目的是在状态方程(2)的约束下利用Pontryagin’s最大值原理求最佳收获使J达到最大值.首先我们借助文献[10]中的方法来证明最佳控制对的存在性.

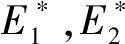
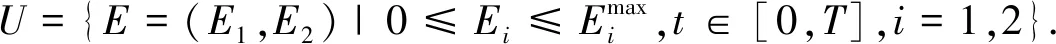
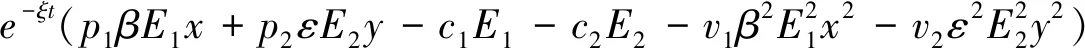
现在我们构造与系统(2)有关的Hamiltonian函数

这里我们引进时滞状态变量

z1(t)=x(t-τ)z2(t)=y(t-τ)

且λi(t),(i=1,2)是伴随函数.

利用Pontryagin’s最大值原理[12]得到下面的定理.

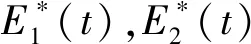
横截条件为λi(T)=0,(i=1,2).同时最佳控制对表达式为

证明 利用Pontryagin’s最大值定理，得到伴随方程

这里χ[0,T-τ]是在区间[0,T-τ]上的特征函数[13].且具有横截条件

λ1(T)=λ2(T)=0

通过使用最佳控制条件，我们令

(7)

求解(7)，得

5 结论

本文建立并讨论了一类具有时滞和捕获的比率依赖捕食模型，首先讨论了系统解的正性和有界性，其次分析了模型平衡点的存在性及稳定性, 得到时滞对轴平衡点的稳定性没有影响，证明了时滞增大可以改变正平衡点的稳定性且导致Hopf分支的产生. 进一步, 利用最优控制理论研究了人们对两种群的最优收获问题，为收获鱼类工作提供了一定的理论指导和建议. 但平衡点的全局动力学行为还不很清楚, 这将是我们进一步研究的课题.