基于自适应数据的GM(1,1)模型背景值优化方法
吴文泽, 黄仁帅,张涛
1.百色学院数学与统计学院,广西 百色 533000 ;2. 广西科技大学理学院,广西 柳州 545006
为了解决不确定或有限小样本的问题,Deng[1]提出了灰色预测模型,GM(1,1)模型是灰色预测的核心和基础部分.作为一种数学模型,GM(1,1)模型已经被广泛应用到经济、管理和工程等众多领域[2~6].
模型预测精度与背景值构造关系密切,许多学者提出了背景值优化的方法.如:Tang[7]提出了一种近似逼近[k-1,k]区间的积分面积的背景值构造方法;Wang[8]通过对GM(1,1)模型的误差分析,利用具有非齐次指数规律的离散数据拟合累积序列,提出了一种优化背景值的新方法;Zhang[9]提出了基于粒子群优化算法搜寻最优背景值的方法;Liu[10]提出一种结合初始值和背景值优化方法以提升模型的预测精度等等.
在现有研究的基础上,本文提出一种自适应数据的优化背景值的方法,极小化预测值和实际值的偏差搜寻最优的αopt,构造新的背景值,提高GM(1,1)模型的预测性能,该方法便于理解且容易实现.数值模拟结果表明,所提出的方法能够提高GM(1,1)模型的预测精度.
1 模型探究
1.1 传统GM(1,1)模型
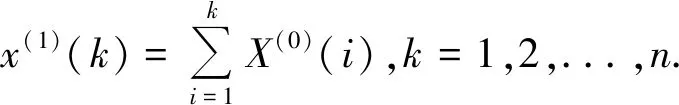
令
1.2 GM(1,1)模型背景值优化
对于GM(1,1)模型的实际背景值z(1)(k),讨论其几何意义[ ].在区间[k-1,k]区间内对白化微分方程两边求积分
(1)
不难发现,背景值的无偏的准确形式为
(2)
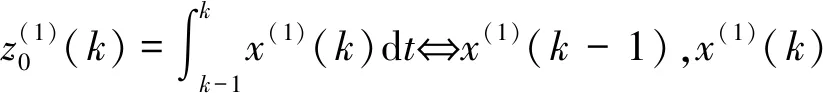
(3)
其中,k=1,2,...,n,αopt为最优权重.
1.3 优化GM(1,1)模型的构建
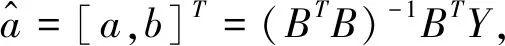
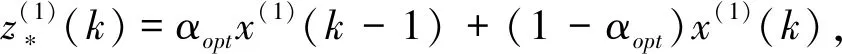
(1)白化微分方程的时间响应方程为x(1)(t)=(x(0)(1)-b/a)e-a(t-1)+b/a.
2 数值模拟
为了验证所提出方法的有效性,本文采用指数函数f(t)=ηeλt生成模拟数据序列[11].令η=2和λ=0.4,则指数函数为f(t)=2e0.4t,当t=1,2,...,7时,生成建模数据如表1所示.为了比较两种模型的精度,本文选取前五个模拟数据作为建模样本,借助MATLAB软件,迭代式(3)的过程104次,找出最优α为0.533 3,总偏差Q=0.001 3,迭代过程如图1所示.
建立传统GM(1,1)模型并得到其参数及灰色微分方程的时间响应函数为
建立优化GM(1,1)模型得到其参数及灰色微分方程的时间响应函数为
通过计算可以得到两种模型的预测值以及模型产生的相对误差(表2),以及两种预测效果图(图2,图3).从表2不难发现,两种模型的预测表现都十分良好,产生的相对误差均小于经验给出的高精度阈值10 %;优化GM(1,1)模型预测产生的相对误差远小于传统GM(1,1)模型预测产生的相对误差;随着t的增加,模型预测产生的误差呈递增的趋势.从图2和图3可以发现,优化GM(1,1)模型预测值更接近实际值,且产生的误差更加趋近于0,表明所提出的方法能够显著提高模型的预测性能.
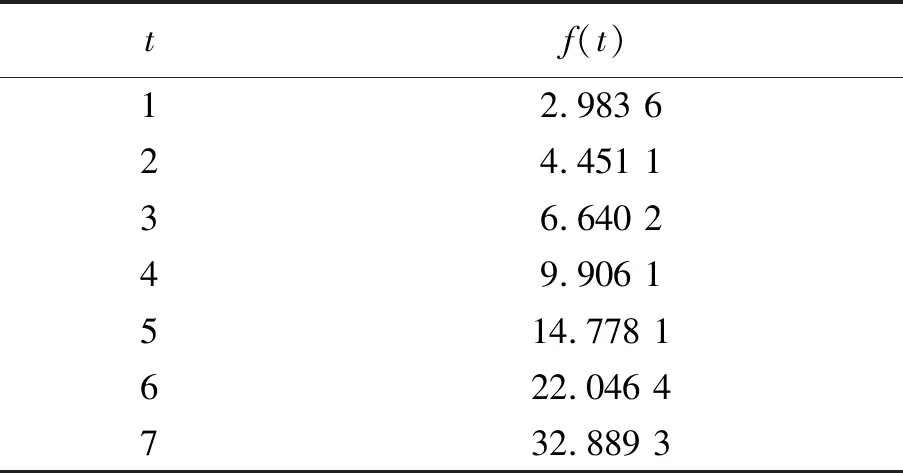
表1 指数函数生成的模拟数据Tab.1 Simulation data from exponential function
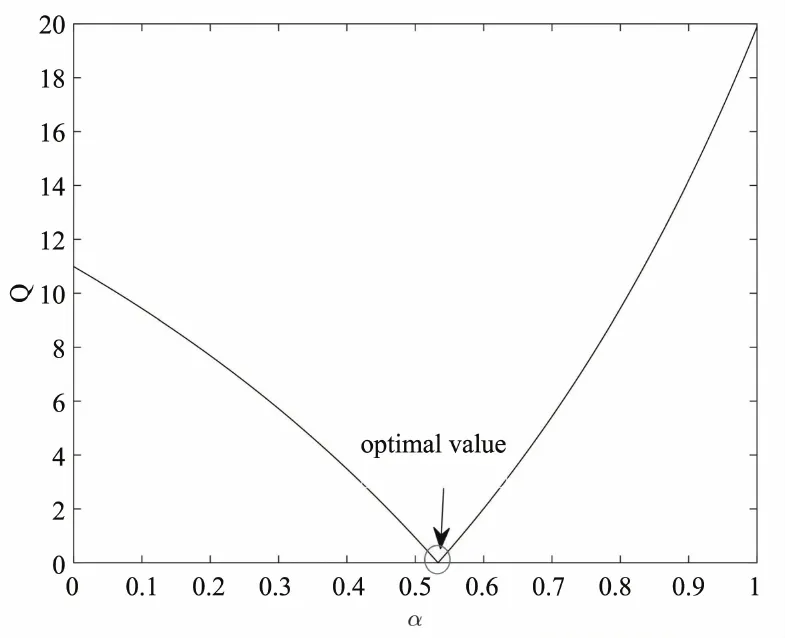
图1α对Q的影响
Fig.1 effects of parameterαonQ
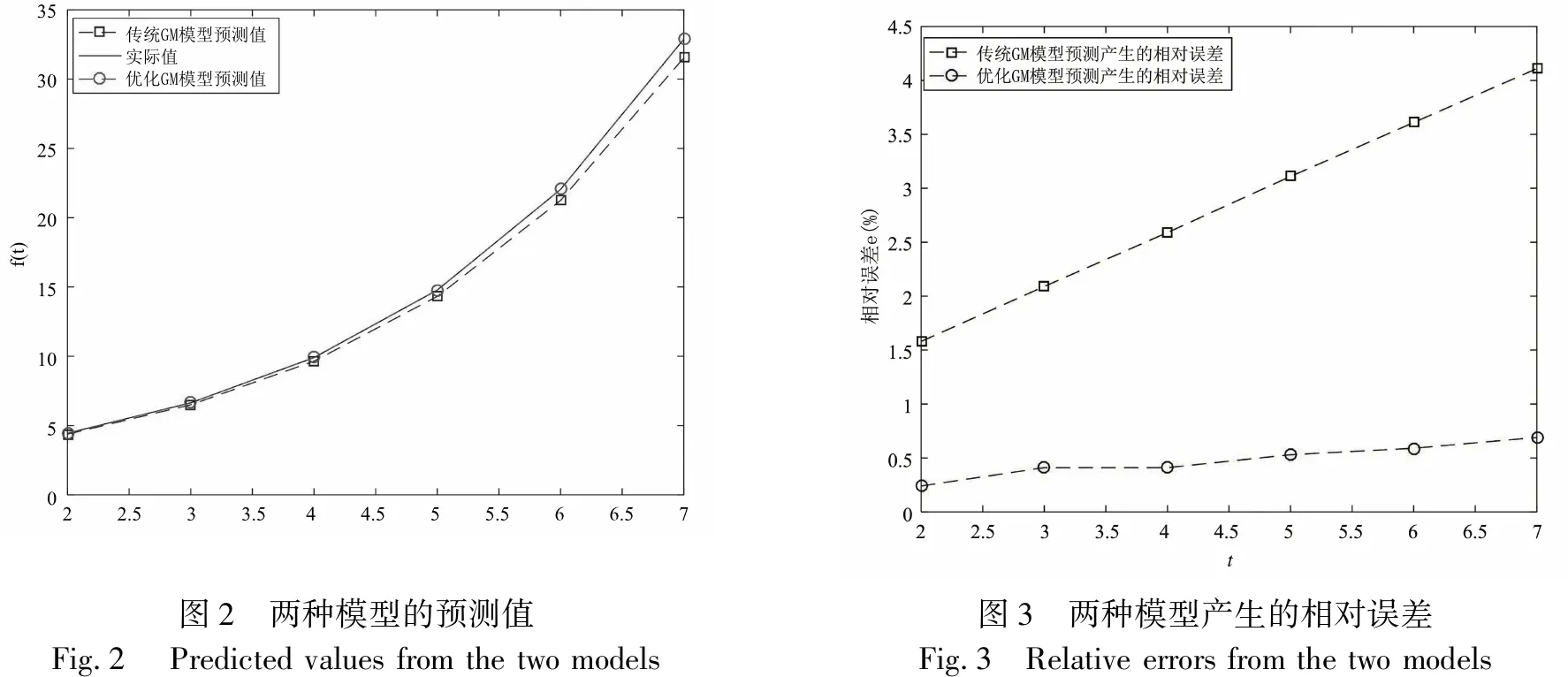
图2 两种模型的预测值Fig.2 Predicted values from the two models图3 两种模型产生的相对误差Fig.3 Relative errors from the two models

表2 两种模型的预测结果Tab.2 Prediction performance of the two models
3 结束语
GM(1,1)模型作为灰色预测模型的基础和核心,有效解决了不确定、有限样本预测问题,但仍然存在改进的空间.本文在已有的文献中,提出一种自适应数据的背景值优化方法,该方法便于理解和易于实现,同时能提高预测的精度.研究表明,该方法是有效和适用的.

