基于FPCA的部分函数型线性模型的复合分位数回归估计

余平

山西师范大学数学与计算机科学学院， 山西 临汾 041000

0 引言

近年来, 随着科学技术的快速发展以及计算机的广泛应用, 数据获取的技术和方法层出不穷，而越来越多的领域所得到的观测数据都具有函数型的特点.比如, 人体生长曲线数据, 气象站观测到的某一地区多年的气温数据, 证券交易市场产生的多只股票的分时或日均成交价、收盘价、涨跌幅、交易量、交易额等数据, 医学诊断中产生的核磁共振数据等[1，2]，它们都是函数型数据的具体实例.也正因如此, 对函数型数据的研究成为当前统计学研究的热点领域之一. 统计学者也提出各种函数型模型对函数型数据进行建模.

在函数型数据分析中, 函数型线性模型是对函数型数据建模最重要、简洁的一种模型. 许多学者对其估计和检验问题进行了深入研究, 取得了丰富的研究成果.然而,在实际生活当中所收集到的数据既包含有一些实值变量数据又包括函数型变量数据. 这时我们只有用函数线性模型描述就不太合适. 因此Shin于2009年对函数型线性模型进行推广, 并提出部分函数型线性模型[3].其定义如下:

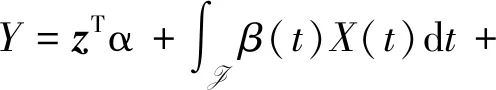
(1)

其中，Y为定义在(Ω,B,P)上的实值响应变量,z=(z1,z2,...,zp)T为2阶矩有限的p维解释变量,X(t)∈L2(J)为0均值随机过程,β(t)为平方可积的斜率函数,为随机误差.不失一般性, 设J=[0,1].那么X(t)为H=L2[0,1]上随机函数. 更多关于模型(1)的统计推断可见Shin[3]、Yu[4]等和Zhou等[5].

上述关于部分函数型线性模型的估计方法都是集中于均值回归, 基于最小二乘法或似然方法. 但是均值回归容易受到异常点的影响, 特别地, 当误差服从非正态分布时,其估计效率或可大打折扣. 为克服均值回归的这一弱点, Koenker和Bassett提出了分位数回归[6].如今分位数回归作为均值回归分析的稳健替代被广泛地用于探索响应变量与协变量之间的潜在关系. 但是目前利用分位数回归对函数型数据进行分析的工作还相对较少. 可参考文献 Cardot等[7]、Kato[8]、Lu等[9]、Zou和Yuan[10]指出, 分位数估计的效率容易受到分位数τ的特定取值的影响，而Zou和Yuan提出的复合分位数估计方法, 其结合多个分位数的信息比利用单个分位数信息估计更有效[10].因此本文将复合分位数回归方法和函数主成分分析方法结合对模型(1)进行估计, 在一定的正则条件下, 我们得到斜率函数的最优收敛速度和参数向量的渐近正态性.

1 估计方法

令(zi,Xi,Yi),i=1,2，...,n为来自模型(1)的独立同分布的一组样本. 为了对函数型回归模型降维和避免过拟合问题, 我们将把预测过程投影到X(t)的协方差函数CX(t,s)=E[X(t)X(s)]的特征向量所张成的空间.具体地,记{(vi(t),λi),i=1,2,...}为CX(t,s)一组标准化特征函数和特征值. 假设特征值无结点, 即是λ1>λ2>...>0.显然v1(t),v2(t),...为L2[0,1]上一组正交基.根据Karhunen-Loève表示定理有

(2)

其中，ξi=〈X(·),vi(·)〉称为X(t)的第i个得分,γj=〈β(·)，vj(·)〉.此外, 定义CX(t,s)的经验形式为

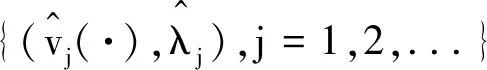
类似地,记

CYX(·)=Cov(Y,X(·))Cz=Var(z)CzY=Cov(z,Y)CzX(·)=Cov(z,X(·))=(Cz1X(·),...,CzpX(·))

其经验形式分别为

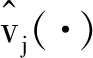
(3)

其中

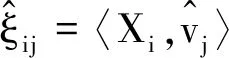
令0<τ1<τ2<...<τK<1,b0k为的真实的τk分位数.根据Zou和Yuan[10]提出复合分位数估计的思想，则估计可以由下面的复合分位数回归关于α.γj,j=1,2,...,m和bk,k=1,2,...,K极小化求解得到

(4)

2 渐进性质

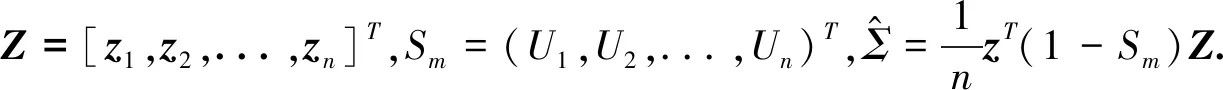
C1 随机函数X(t)和随机得分变量ξi满足

C2 协方差函数CX(t,s)的特征值λi和得分系数γj分别满足下列条件:

(a)存在常数c和a>1使得

c-1i-a≤λi≤ci-aλi-λi+1≥ci-a-1i≥1

(b)存在常数c和b>a/2+1使得

|γj|≤cj-bj≥1

C3 调整参数m满足m～n1/(a+2b).

C4 随机向量z和随机误差具有有限的四阶矩, 亦即是E‖z‖4<∞,E[4]<∞.

C5 存在常数c使得对于每个k有下式成立

|〈CzkX,vj〉|≤cj-(a+b)k≥1

C7fi在其整个支撑有界, 在点b0k的邻域内fi存在大于0的下界且其一阶导数存在且有界.

注1 条件C1～C2是函数型线性分位数模型中常见的基本条件, 可以参考Shin[3]和 Kato等[8].条件C7是分位数估计中常见的假设条件, 可参考Wang等[11].

定理1 假设条件C1～C7成立, 则有

(5)

定理2 在定理1成立的条件下, 则有

(6)

其中

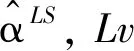
推论1 在定理1成立的条件下, 记α的复合分位数估计分别关于其最小二乘估计和分位数估计的渐近相对效为ARELS和AREQR, 则有

3 模拟研究

本节我们通过数值试验研究所提出的复合分位数回归估计方法在有限样本下的实际表现. 从以下模型产生数据

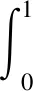
(7)

其中,z=(Z1,Z2)T,Z1～N(0,1),Z2服从两点分布, 其中取1的概率为0.5.α=(α1,α2)T=(1,1.5)T.函数型线性部分产生和Yu等[4]相同,即

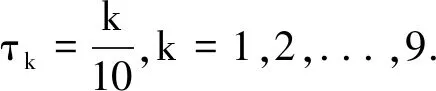
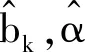
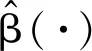
重复模拟200次, 在三种随机误差和不同样本容量情形下, 表1～表2给出了参数向量α估计的均方误差(MSE)以及其分量估计的偏差(Bias)和标准差(Sd),表2给出斜率函数β(t)估计的RASE.由表1～表2可以看出:(1)在给定的分布下, Sd,MSE和RASE都随着样本容量n的增加而减小,参数部分估计为渐近无偏的，这也表明提出的估计方法具有相合性;(2)当误差来自N(0,1) 时, 正如所预料的那样,LS表现最优, CQR估计略优于LS估计;(3)当误差来自厚尾t(3)或者混合正态分布0.9N(0,1)+0.1N(0,102)时, CQR估计表现最好, LS表现比较差最差,这也说明CQR估计和LAD估计对于异常值和厚尾分布的随机误差具有稳健性.

综上, 这些结果说明复合分位数估计对于处理函数型解释变量具有厚尾特征或者异常值的响应的分析是非常必要和可行的.

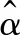
表1 不同随机误差下的模拟结果Tab.1 Simulation results for with different random errors

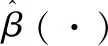
表2 不同随机误差下情形斜率函数的RASETab.2 Simulation results of RASE for (·)with different random errors

4 附录

4.1 定理1的证明

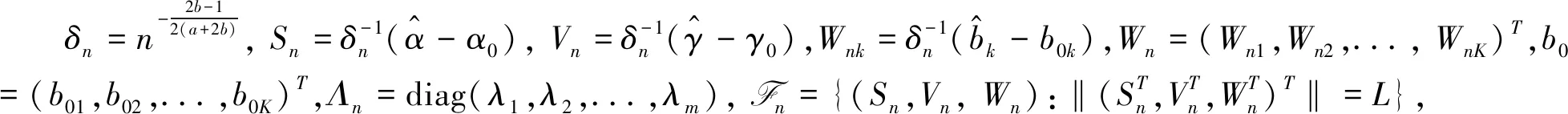
(8)

Pn(wn,un)=Qn(α0+δnSn,γ0+δnVn,b0+δnun)-Qn(α0,γ0,b0)

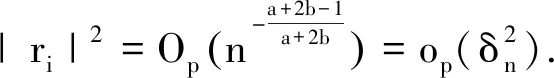
(9)

其中

(10)

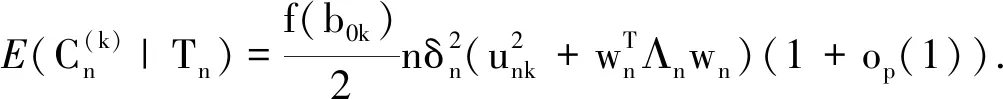
(11)

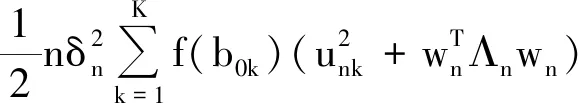
(12)

4.2 定理2的证明

(13)

(14)

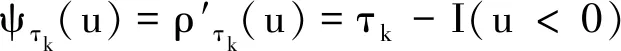
(15)

(16)

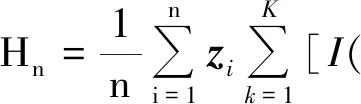
利用Taylor公式和定理1简单计算可知

因此, 我们可得

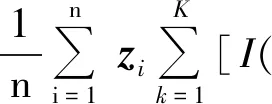
(17)

类似可得

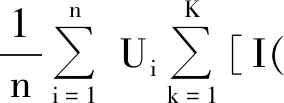
(18)

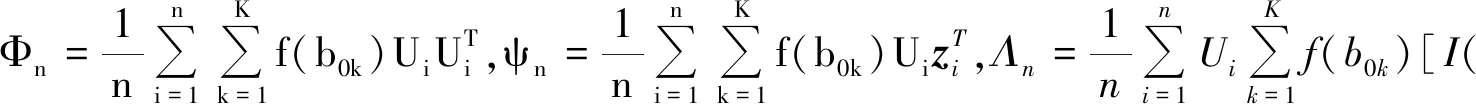
(19)

把(19)式带入(18)式中可得

(20)

注意到

(21)

(22)

根据式(20)～式(22)简单计算可知

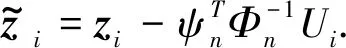
同时注意到

调用中心极限定理可知

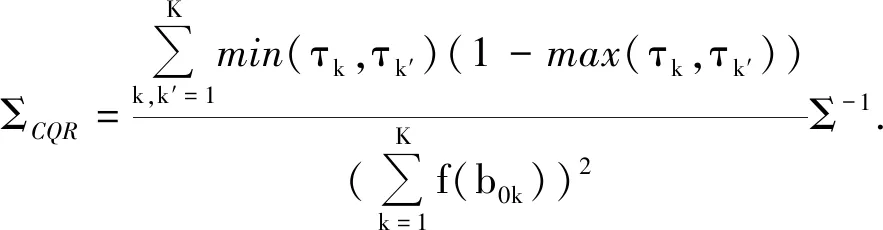
证毕.