高温作业的热传导与有限差分求解
杨云霞
山西工程技术学院, 山西 阳泉 045000
1 高温作业专业服装设计问题
高温作用专用服装一般由三层织物材料构成,分别记为第I、II、III层,第I层与外界环境接触,第III层与皮肤之间有一定空隙,该空隙记为IV层.为了设计高温作用专用服装,现将37 ℃(保持不变)的假人放置在高温实验室中,测量假人皮肤外侧的温度.下面我们利用数学模型[1,2]来确定假人皮肤外侧的温度变化情况,并解决下面两个问题:
(1)给出专用服装材料的一些参数值(表1),设环境温度为75 ℃、第II层和第IV层厚度分别为6 mm和5 mm,工作时间为90 min.通过实验,测量得到了假人皮肤外侧的温度.建立数学模型[3,4],计算温度分布.

表1 专用服装材料的参数值Tab.1 The parameter value of special clothing material
(2)设环境温度为65 ℃,第IV层的厚度为5.5 mm,确定第II层的最优厚度,同时要保证工作60 min时,假人皮肤外侧温度不能超过47 ℃,且超过44 ℃的时间不超过5 min.
2 问题分析
将高温作用专业服装设计问题化简为图1.设织物材料I层、II层、III层、IV层的厚度分别为Li(i=I、II、III、IV),则上述两个问题可简化成下面的数学问题[5]:
(1)已知T(x<0,t)=75 ℃,LII=6 mm和LIV=5.5 mm;根据假人皮肤外侧的温度可知T(x=x4,t),其中,0 min (2)已知T(x<0,t)=65 ℃,LIV=5.5 mm.求T(x4,t<60 min)≤47 ℃ 且T(x4,t<55 min)≤44 ℃的L2最小值. 图1 一维平面内热传导示意图,其中 dummy(假人)层表示假人皮肤到体内的厚度 高温作业专用服装设计的问题实质为一维的热传导问题,一维无热源热传导方程[6]是 (1) 其中,t表示时间,ρ表示密度,cp为比热,k为热传导率,x表示一维空间坐标.在一维空间中,密度、比热和热传导率在时间上都是常数,则(1)式可化简为 (2) α称为热扩散系数. 为了解决空间温度随时间的变化T(x,t),我们用有限差分法求解T(x,t).因此我们先对空间和时间进行离散化,再求解离散点上的温度,下图2为离散后的节点示意图. (3) 图2 有限差分的空间和时间节点示意图 (4) 则(1)式可化为 (5) 由(5)式可得n时间步和n+1时间步温度场的关系.由此关系,如果知道n时间步的温度场,则可求得n+1时间步的温度场. 热阻[7]是指在有温度差的情形下,物体抵抗传热的能力.导热率越好的物体,热阻通常会比较低.热阻可定义为 (6) 其中,q表示热流,R表示热阻.热传导率与热阻的关系可表示为 (7) I、 II、III、IV四层总热阻为 (8) 流过任意截面的热流相等,因此可求得 (9) 首先根据表1的数据定义相关参数. rho=[300,862,74.2,1.18];% [kg/m3] 密度cp=[1377,2100,1726,1005];% [J/kg/K] 比 热k=[0.082, 0.370, 0.045, 0.028];%[W/m/K] 热传导率L=[0.6,6.0,3.6,5.0];%[mm]厚度xL=cumsum(L)[x1, x2, x3, x4]%[mm]材料层接面位置,即图1中的 [x1, x2, x3, x4]mm2m =1e-3;% 将 mm 转为 m 的系数 再定义有限差分的空间和时间的网络节点信息. dx=0.3;%[mm]空间网格尺寸xmax = sum(L);%[mm]模拟区域尺寸x=0:dx:xmax;% [mm]网格节点坐标nx=length(x);% 节点数目ind=round(cumsum(L)/dx);% 不同材料层间的交接点序号dt=4e-4;%[s]时间步长tmax = 90∗60;%[s]最大仿真时间t=0:dt:tmax;%[s]时间节点nt=length(t);%时间节点数 cfl=dt/(dx∗mm2m)2./rho./cp; % 注意这里 dx∗mm2m 是dx转为以 m 为单位的长度[~,~,id]=histcounts(x,cumsum([0,L]));% 找出每个节点所属的层kx=k(id);%[m2/s]每个节点所属层的热传导率cflx=cfl(id);%每个节点所属层的 cfl 利用有限差分法解决一维平面的热传导问题,MATLAB[8]编程可获得稳态时的温度分布数值解(图3)和不同时刻的温度分布(图4). 图3 有限差分得到的稳态时的温度分布数值解 问题2实际所求为假人皮肤表面的温度,即T(xIV,t).假人体内温度控制在37 ℃,由此可得边界条件为: T(x=0,t)=65 ℃T(x=xd,t)=37 ℃ (10) 问题中没有给出假人的皮厚Ld(即皮肤外侧到体内的距离)、密度、比热和导热系数等信息.如果这些信息是已知的,那么在第一问中,若将右侧边界设置为T(x=xd,t)=37 ℃,则可以通过有限差分计算得到不同时刻假人皮肤表面的温度T(x=xIV,t),我们可以根据该条件猜测假人的一些关键信息. 假设假人是由均匀统一的材,因此我们可以求出假人的热阻.在问题1最终稳态下,T(x=xIV)=48.08,而T(x=xd)=37.由热阻定义可知: (11) 由(9)通过MATLAB编程可求出q,Rd的解.解得Rd=0.116 1. 我们假设假人的皮厚L4=2 mm,该假设对结果没有什么影响,如果假人皮厚,热传导率就小,反之,热传导率就大,但最终隔热效果是一样的.为了计算需指定一个厚度,然后便可求得热传导率.由此可得热传导率 图4 不同时刻的空间温度分布(动态图)Fig.4 Spatial temperature distribution at different times (dynamic diagram) kd=0.086 1 从而可以绘制出假人的最终温度分布图(图5). 图5 由热阻理论得到的稳态时的温度分布理论解 由于假人的比热cpd和密度ρd均未知,但在计算中,我们只需知道两者的乘积,这里不妨假设假人的密度是ρd=1 000 kg/m3(同真人密度接近).接下来根据问题1来确定假人的比热cpd,我们采用二分法求假人的比热cpd.实质上就是不断的猜想,直到猜出的cpd能够获得假人皮肤表面温度的数据.具体步骤如下: 1.初始设置cpdmax=3000,cpdmin=1000; 2.cpd=(cpdmax+cpdmin)/2,如果计算得到的T(xIV,t)总体小于假人皮肤表面温度的数据,那么cpdmax<-cpd,反之cpdmin<-cpd; 3.若cpdmax-cpdmin>1,则跳到2,否则停止,并返回cpd=(cpdmax+cpdmin)/2 . MATLAB编程求得cpd=1 415. 根据假人的相关信息,下面我们可以求解最优厚度,由表1可知,0.6 1.假设Liimin=0.6,Liimax=25; 2.Lii=(Liimin+Liimax)/2,如果计算得到的T(x=xIV,t=60)>47或T(x=xIV,t=55)>44,说明我们求得的厚度比较小,则Liimin<-Lii,否则Liimax<- Lii; 3.如果Liimax-Liimin>0.1,则跳到2,否则停止,同时返回Lii=Liimax、,此时的Lii为第II层的最优厚度. MATLAB编程求得第II层的最优厚度12.23 mm. 文章是在给定的一些假设和条件下,将实际问题化为数学问题,建立数学模型,利用MATLAB编程,解决了高温作用专业服装设计的问题,其结果可以供服装设计者参考,使设计高温作业服装降低研发成本,缩短研发周期.我们在整个求解过程中只考虑了热传导,事实上热传递还有两种:热辐射和空气对流.由于第Ⅳ层的厚度很小,对于后面两种的影响几乎可以忽略不计,但是,既然存在,多少都会对结果有一些影响.另外,也有一些影响因素没有考虑到,导致计算的结果可能会与事实产生了一定的偏差.
Fig.1 Heat conduction in a one-dimensional plane,The dummy layer is the thickness of the dummy skin to the body3 模型建立
3.1 一维热传导问题与有限差分求解

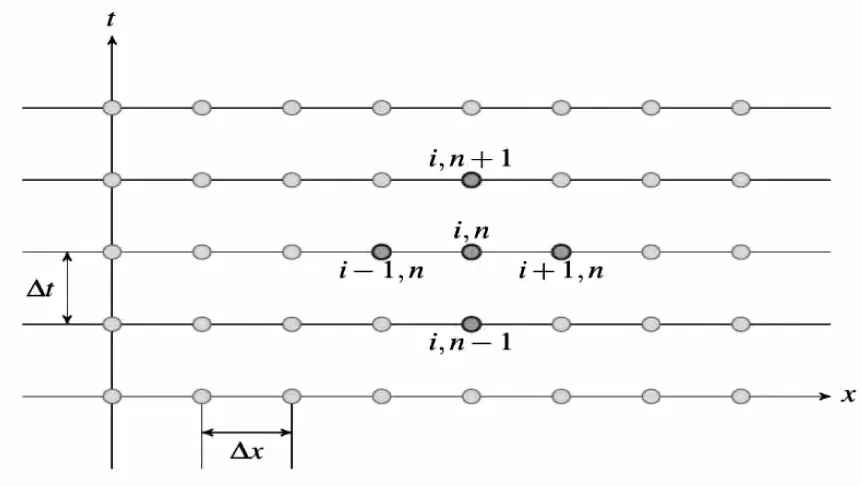
Fig.2 Schematic diagram of finite difference space and time nodes3.2 热阻
4 问题的求解
4.1 问题1的求解




Fig.3 The numerical solution of steady-state temperature distribution obtained by finite difference method4.2 问题2的求解

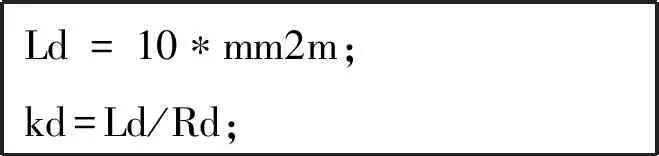

Fig.5 The theoretical solution of steady-state temperature distribution obtained from thermal resistance theory5 结束语

